受载结构中SH0波与裂纹作用的非线性散射场的数值研究*

陈荟键, 朱清锋, 苗鸿臣, 冯志强

(西南交通大学 力学与航空航天学院, 成都 611756)

0 引 言

超声导波具有传播距离远、能量衰减小、对结构损伤敏感等优点,在结构健康监测和无损检测领域被广泛关注[1]．传统的线性导波技术基于导波的线性效应,主要通过测试声速、衰减、反射率和透射率等参数来检测缺陷．然而,线性导波通常仅能检测与波长相当的缺陷,如孔洞、宏观裂纹等,而对材料中的初期损伤不敏感．非线性超声导波兼具线性导波快速检测和非线性超声对材料初始损伤高灵敏度识别的双重优点[2]．以接触声非线性效应为例,超声导波与微裂纹作用过程中的接触声非线性效应可以引起高次谐波、零频响应等非线性超声特征[3],这些特征可以用于识别线性超声无法识别的微裂纹．

板壳结构中的零阶水平剪切波(SH0波)因其独特的非频散特性,在结构健康监测和无损检测中具有重要的应用前景[4]．洞悉SH0波与裂纹的作用规律对于发展基于SH0波的裂纹检测技术具有重要的意义．当前SH0波与裂纹的线性散射规律已经得到了较为深入的研究[5-8],而关于SH0波与微裂纹的接触声非线性散射规律的研究成果还比较匮乏,特别是结构外部荷载对SH0波非线性散射特征的影响规律尚未见报道．因此,有必要研究受载条件下SH0波与微裂纹作用的非线性散射规律．由于此时结构中存在初始应力场和声场的耦合,使得SH0波与微裂纹作用时的接触声非线性作用十分复杂,因此需要借助数值仿真对该问题进行分析．有限元法[9]具有易实现、灵活性高等优点,是模拟结构中导波传播最常用的方法之一．然而,由于导波具有频率高、波长短的特点,使得传统有限元法在求解此问题时,对网格密度的要求高,计算效率较低．时域谱元法[10]结合了伪谱法高阶多项式快速收敛性和有限元法复杂几何适应性的优点,能够以较小的计算代价求解导波传播问题．然而,谱单元对复杂几何结构的离散能力不如有限元法．

为求解接触声非线性问题,需要准确描述在超声波作用下裂纹面的张开、闭合以及滑移等接触摩擦行为[3]．目前求解接触问题主要的方法有罚函数法和Lagrange乘子法．罚函数方法[11-12]容易实现且收敛速度快,但是罚因子的选取较为困难．若选取的罚因子过小,则接触穿透量较大,从而影响数值精度;若增大罚因子,虽然可以更加符合接触条件,但是这样又会引起局部接触计算的不稳定,同时时间步长还需设置得非常小．此外,罚函数法难以考虑接触计算时的多点耦合效应,而在实际的接触计算中,接触点之间是相互影响的．Lagrange乘子法[13]能够精确地满足物体间的法向接触边界,但是系统中由于引入了Lagrange乘子,使得方程变量增多,从而增加了整个问题的计算量．由De Saxcé和Feng[14-15]提出的双势接触方法,在不增加自由度的前提下,既能够准确地满足法向的Signorini接触条件,又能满足切向的Coulomb摩擦定律,在处理接触问题上具有较高的精度和效率．Chen等[16]结合谱元法和双势接触方法,发展了可以高效计算接触声非线性问题的双势谱方法,证明了双势方法可以准确处理波动接触问题．

本文在双势谱方法的基础上,进一步通过mortar方法将谱单元和有限单元进行耦合,以此研究了SH0波与裂纹作用的非线性散射规律．首先,介绍了处理有限单元/谱单元耦合界面的mortar方法的基本理论．其次,介绍了用于刻画导波与微裂纹作用时,裂纹面的接触摩擦行为的双势接触理论．接着,本文介绍了一种预处理半显式算法,该算法囊括了包含附加界面力的局部接触力的隐式求解与全局位移的显式求解,其可以在保证计算效率的同时而不牺牲数值精度．最后,通过发展的数值方法计算了自由状态和单轴受载状态下SH0波与微裂纹作用的非线性散射规律,并分析了应力大小对非线性散射场的影响．

1 数值方法的理论基础

1.1 Mortar方法的基本理论

Mortar方法是一种非协调区域分解算法,它允许将求解区域分解为多个子区域,对各个子域分别进行建模和剖分,然后在各个区域以最适合子域特征的方式进行离散．在mortar方法中,各个子域交界面处的边界节点不需要严格逐点匹配,而是通过约束方程弱形式建立具有最佳精度的mortar条件来使得界面处的场变量得以传递,以此来保证不同子域之间的连续性．Bernardi等[17]最先于1994年提出了mortar元法的概念．目前mortar方法已被成功应用于处理弹性动力学问题[18-19]、流体力学问题[20]、接触摩擦问题[21-22]等．

如图1所示,考虑由两个互不重叠的子域ΩFE和ΩSFE构成的域Ω,满足Ω=ΩFE∪ΩSFE和ΩFE∩ΩSFE=∅．其中Ω为研究总域;ΩFE采用有限单元离散,称为有限元区域;ΩSFE采用谱单元离散,称为谱单元区域．两个子域之间的交界面用γ表示,即γ=∂ΩFE∩∂ΩSFE．由于两个子域采用不同的单元类型进行离散,因此在界面γ处存在不匹配性．这种不匹配性主要体现在两个方面:一是几何上的不匹配．由于有限单元和谱单元在网格划分以及单元类型上的差异,界面处两个区域的单元节点往往是不重合的．二是插值函数上的不匹配．有限元采用的是低阶的插值形函数,而谱单元采用高阶多项式作为插值形函数,因此两者在界面两侧拥有不同的形函数空间．

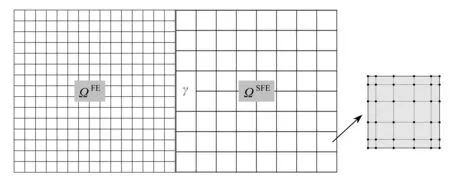
图1 有限元和谱单元耦合示意图Fig. 1 Schematic diagram of the coupling of finite elements and spectral elements

考虑界面γ处的位移连续性条件:

(1)

式中,uFE和uSFE分别为有限元区域和谱单元区域的位移场;Ni是和界面节点相关的有限单元的形函数;i表示界面的第i个节点;Nf为有限元区域界面节点的个数．为了使用显式时间积分,位移连续性条件用等价的速度连续性条件替代,即

(2)

上式约束条件一般可称为mortar条件,关于mortar条件的数学描述可参考文献[18,23]．

Mortar方法的目标是在整个界面γ上满足连续性条件和运动平衡方程．既要保证两个子域在界面上不会发生分离和重叠,又要保证整个界面的动力平衡．后者可以通过引入适当的界面相互作用力来实现,本文采用Lagrange乘子法求解该界面力．在不考虑接触力和材料阻尼的条件下,系统的控制方程可以写为[18]

(3)

(4)

其中,G为界面耦合矩阵,其只和界面上节点的初始位置相关,在整个动力学求解过程只需计算一次[19];Rγ为附加界面力矢量,可通过Lagrange乘子法求解得到

Rγ=GTλ,

(5)

式中,λ为Lagrange乘子,将式(5)代入式(3),并对等式两边同时乘以GM-1,可以得到

(6)

引入中心差分格式

(7)

(8)

与中间时刻速度表达式

(9)

上式两端同时乘以G,并做等式变换可得

(10)

将上式代入式(6),并结合式(4)可得

(11)

至此,Lagrange乘子λ可按照常规线性方程组Ax=B的格式进行求解．一旦求解得到λ,便可通过式(5)求解得到附加界面力矢量Rγ,然后将求解得到的Rγ代入式(3),再通过时间积分算法便可获得位移场．

1.2 双势接触理论

双势理论[14]由De Saxcé和Feng于1991年提出,该理论以Legendre定理为基础,通过Fenchel不等式变换,建立了一组能够处理对偶变量的方程．通过对材料模型能量势函数形式进行分析,将材料分为显式标准材料和隐式标准材料,在此基础上,提出了双势函数的概念．

对于接触问题,双势函数Fb可以写成如下形式:

(12)

(13)

(14)

基于式(12),可以得到接触问题中双势函数的次法向准则,即

(15)

νFb(-xα,rα*)-νFb(-xα,rα)≥[(rα-νxα)-rα]·(rα*-rα),

(16)

式中,ν>0,其值的选择确保了数值计算的收敛性,一般可由减缩的接触柔度矩阵的最小特征值决定[25]．从上式的右端项可知,rα为增广Lagrange接触力rα*的临近点．因此,可将增广Lagrange接触力rα*表示为

(17)

式中,rα*在接触迭代计算中又被称为预测接触力．得到预测接触力后再在Coulomb摩擦锥上进行投影,从而得到真实接触力,即

rα=PKμ(rα*)．

(18)

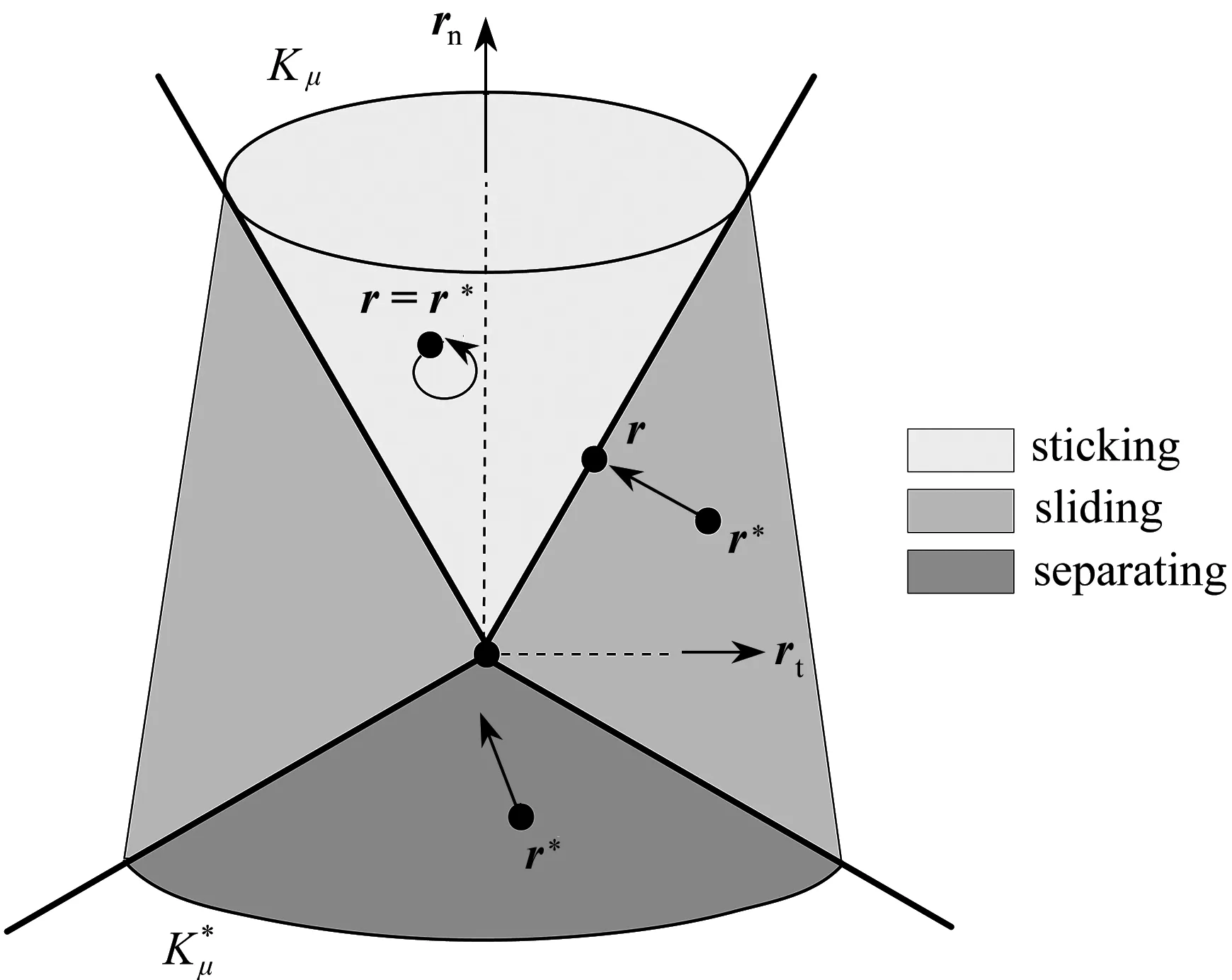
图2 Coulomb摩擦锥示意图Fig. 2 Schematic diagram of Coulomb’s frictional cone

(19)

该投影方程已被严格证明等效于不等式(16),并且在数值计算中,具有出良好的精确性和鲁棒性[26]．

1.3 预处理半显式算法

在考虑接触力以及附加界面力的情况下,系统的控制方程可以写为

(20)

引入有限差分格式:

(21)

将式(21)代入式(20),可以得到

(22)

对于线弹性材料,一般可取C=αM,其中α为质量阻尼系数．代入式(22),可预定义以下参数:

(23)

此时可将式(22)重写为

ut+Δt=(ψ1+ψ2)-1·[(Fext)t-(Fint)t+(Rγ)t+(Rc)t+Δt+2ψ1ut-(ψ1-ψ2)ut-Δt]．

(24)

上式可进一步写成关于每一个节点自由度i的显式表达式:

(25)

从上式可以看出,即便在附加界面力通过Lagrange乘子法求解得到后,全局位移和全局接触力仍为未知量,不能直接求解．本文采取分开求解的策略,先引入接触映射关系,通过隐式迭代算法求解局部接触力r,然后通过局部接触力与全局接触力的关系将局部接触力转换为全局接触力Rc,最后将全局接触力引入式(24)中,即可显式地求解剩余的未知量u．

在接触运动学中,局部接触力r与全局接触力Rc以及局部接触位移x与全局接触位移u之间的关系可写为[16]

(26)

式中,g为接触系统中的接触点与投影点之间的初始间隙矢量．

结合式(24)和(26),有

x=T(ψ1+ψ2)-1TTrt+Δt+

T(ψ1+ψ2)-1[(Fext)t-(Fint)t+(Rγ)t+2ψ1ut-(ψ1-ψ2)ut-Δt]+g．

(27)

定义

(28)

式(27)可以进一步写为

(29)

其中,W是接触系统中基于质量矩阵构建的Delassus算子．需要注意的是,由于质量矩阵的对角性质,W的计算将会非常迅速．在包含Nc个接触点的减缩接触系统中,对每一个接触点α而言,局部相对位移xα和局部接触力rα之间有如下关系:

(30)

式中,Wαβ=Tα(ψ1+ψ2)-1(Tβ)T为影响矩阵,其描述了接触点α和β之间的接触耦合效应．换言之,对于每一个接触点α,都考虑了其他接触点β(β≠α)对α的接触力的贡献．

结合式(18)和(30),减缩系统下接触力的求解可以转换为寻找χ以满足f(χ)=0,即

(31)

其中

(32)

(33)

隐式方程(32)可采用Uzawa算法[27]进行局部迭代求解,该算法主要包括“预测-修正”步骤,即

(34)

式中,i和i+1为迭代数．如前所述,通过Uzawa算法求得局部接触力,然后通过局部接触力与全局接触力的关系式(26)将局部接触力转换为全局接触力,最后将全局接触力代入式(25)中,即可显式地求解未知量u．

2 SH0波与微裂纹作用的非线性散射场研究

2.1 模型设置

图3为SH0波与不同角度微裂纹作用的非线性散射场的计算模型．板的面内尺寸为100 mm×100 mm,采用平面应力模型进行计算,所用材料为铝,其弹性模量为70 GPa,Poisson比为0.3,质量密度为2 700 kg/m3．在板的上下边界施加预拉/压应力p,同时在板的四周布置长度为10 mm的渐增阻尼边界吸收层[28],最大阻尼系数αmax=107．坐标原点设置在板中心位置．微裂纹角度θ为裂纹长度方向与x轴正方向的夹角,微裂纹几何中心与板中心重合,其长度设置为6 mm．采用有限单元/谱单元混合单元对板进行离散,其中含裂纹的圆形区域(半径R=20 mm)采用有限单元离散,不含缺陷的外部区域采用谱单元离散．入射SH0波由板左边界长60 mm的对称段上施加沿y方向的激励力产生,激励波形为Hanning窗调制的五周期正弦波,中心频率为500 kHz,幅值为100 N．为方便提取散射场信号,取有限元区域的外边界节点作为散射场的响应点．

图3 SH0波与微裂纹作用的非线性散射场计算模型Fig. 3 The calculation model for the nonlinear scattering characteristics of the SH0 wave encountering cracks in prestressed plates

如图4所示,得益于本文介绍的处理有限元/谱单元耦合界面的mortar方法,当研究裂纹角度对SH0波散射特性的影响时,可以把外部谱单元区域固定,然后将内部包含微裂纹的有限元区域进行整体旋转,即可得到新的裂纹模型,旋转后该区域的节点坐标可通过初始节点坐标向量做简单的张量变换求得．该策略只需要建立一次裂纹模型便可实现任意角度的裂纹建模,因而可以巧妙地避免传统方法在处理此类问题时对裂纹进行重复建模、网格重新划分的麻烦．

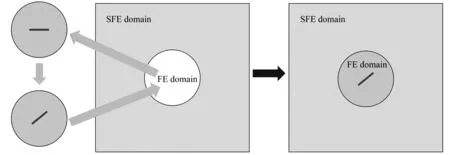
图4 不同角度裂纹建模原理图Fig. 4 Schematic diagram of the crack modeling at different angles

2.2 自由板中的非线性散射场

本小节探究了自由板(p=0)中SH0波与微裂纹作用的非线性散射规律．取θ=60°,图5展示了SH0波与微裂纹作用前后的总位移云图．可以观察到:① 有限元/谱单元交界面处网格不匹配对SH0波在结构中的传播没有任何影响,验证了不同单元类型区域之间的连续性,证明了本文中mortar方法的有效性;② 当SH0波传到边界时,绝大部分能量被吸收掉,反射信号基本消失,证明了渐增阻尼边界吸收层的有效性;③ 当SH0波与微裂纹作用后,会向外辐射一个新的散射声场,该声场在不同方向有不同的信号强度．

图5 不同时刻的非线性散射总位移云图Fig. 5 The nonlinear scattering fields at different moments

图6为提取含微裂纹结构中M点的时域信号以及对应的频谱图．作为对比,图6中同时给出了对应的不含裂纹即完整结构的计算结果．从图6(a)可以看出,两组信号仅在幅值上有所不同,但波形上的差异并不明显．为进一步区分这两种情况,我们将两组时域信号做快速Fourier变换,可以得到对应的频谱图,如图6(b)所示．从频谱图可以直观地分辨出两种工况存在不同的频率分量．具体地,对于无损伤结构,频谱图中只包含500 kHz激励频率分量;而对于含微裂纹的结构,在频谱图中,除激励频率500 kHz之外,还产生了1 000 kHz,1 500 kHz,2 000 kHz等明显的高次谐波分量．该结果表明,可以通过SH0波与微裂纹相互作用产生的高次谐波分量来对微裂纹进行有效识别．

图6 无损伤和含微裂纹损伤工况下,时域信号和对应频谱图的比较Fig. 6 Comparison of time domain signals and corresponding frequency spectrums between the pristine case and the microcrack damaged case

实际情况下的微裂纹的取向往往是未知的,而工程中对裂纹扩展方向的判断又至关重要[29]．因此,建立非线性散射规律与微裂纹取向角之间的关系,对于裂纹检测传感器的布置以及传感信号识别具有重要的意义．需要注意的是,由于SH0波仅有一个垂直于传播方向的面内位移分量,因此极坐标系下的切向位移可以用来表示SH0波模态[4]．

图7展示了SH0波与不同角度微裂纹作用后的切向位移时程对应的二次谐波归一化非线性散射场(SH0-SH0模式)．可以看出,二次谐波散射场随着微裂纹取向的变化而敏感变化．具体地,对于0°微裂纹(图7(a)),二次谐波散射场具有很好的对称性,且只存在一个明显的指向水平向左的主瓣,而微裂纹的取向角恰好与主瓣的对称轴角度一致．对于20°,30°,40°,60°微裂纹(图7(b)—7(e)),二次谐波散射场均呈现良好的对称性,且微裂纹的取向角与散射场中分布于裂纹两侧的主瓣中轴线的角度几乎一致．而对于80°微裂纹(图7(f)),虽然二次谐波散射场依然呈现较好的对称性,但是指向性相对于其他角度裂纹的散射场变弱．这是由于90°微裂纹的裂纹面平行于SH0波的质点振动方向,当裂纹面处于自由应力状态时,即不存在法向预应力时,不会发生接触声非线性效应．因此,当微裂纹角度接近于90°时,接触声非线性效应减弱,从而导致非线性散射场的指向性会在一定程度上被破坏．即便如此,仍然可以通过散射场的对称性对微裂纹的取向进行大致的判断．由此可见,切向位移的二次谐波散射场可对微裂纹取向进行定量表征．本文的计算结果与文献[30]吻合良好,证明了本文发展的数值方法的有效性和正确性．

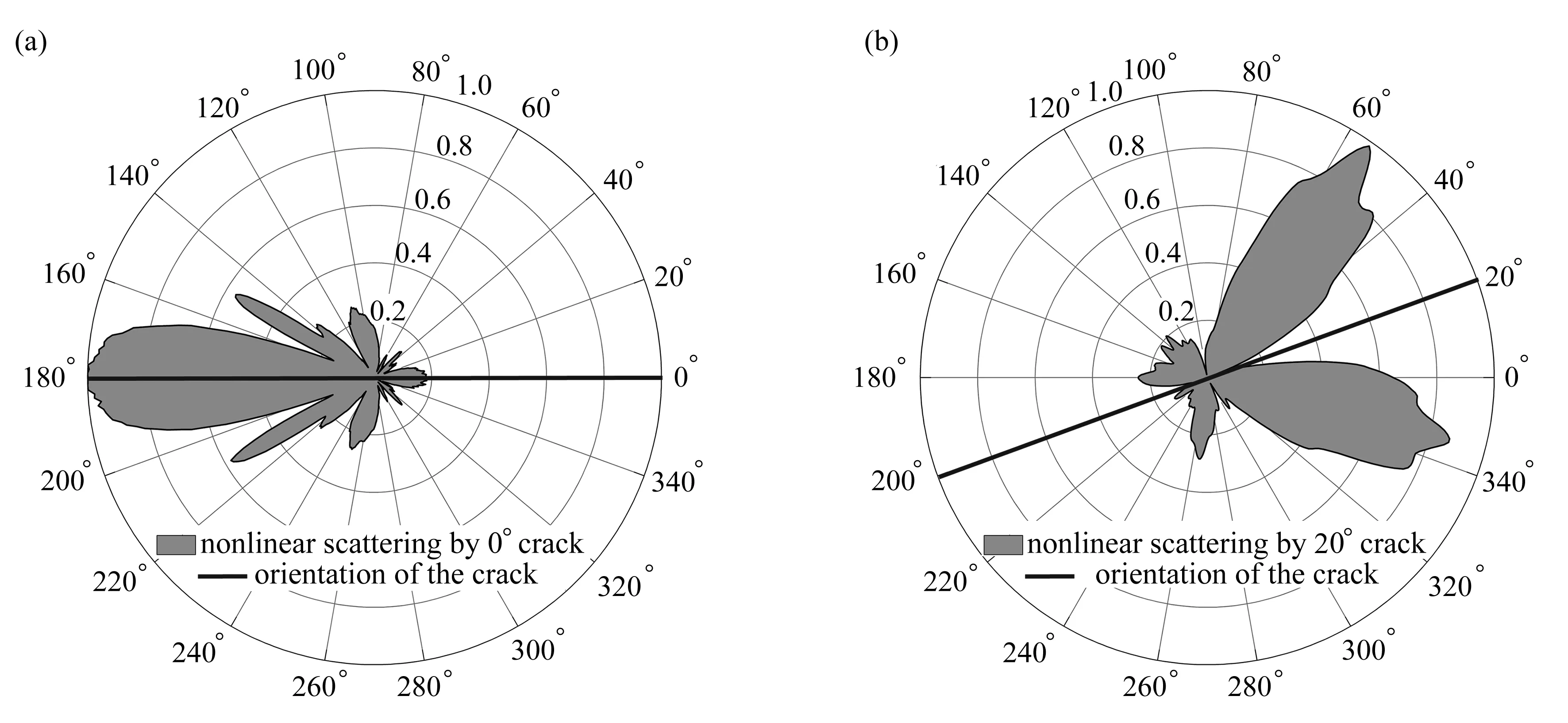
图7 不同微裂纹取向对应的切向位移二次谐波归一化散射场Fig. 7 Normalized scattering fields of the 2nd harmonics for different microcrack orientations

2.3 预应力板中的非线性散射场

由2.2小节的结果可知,在结构处于自由状态时,通过SH0波与微裂纹作用的二次谐波散射场的指向性和对称性可以很好地对微裂纹的取向进行表征．本小节继续探讨受载条件下SH0波的非线性散射场．需要注意的是,当考虑受力状态下的非线性散射场时,整个计算过程可分为两步进行．第一步,计算外部载荷对系统产生的初始应力场;第二步,在初始应力场的基础上计算SH0波与微裂纹的非线性作用．

图8为单轴拉伸状态下的SH0波与不同角度微裂纹作用后的切向位移二次谐波归一化非线性散射场．从图中可以看出,预拉应力并不会破坏散射场的指向性和对称性．这说明即使结构处于预拉应力状态下,仍然可以通过二次谐波散射场来对结构中微裂纹的取向进行判断．此外,还可以观察到,拉应力会对非线性散射场的幅值产生明显的影响．具体来说,二次谐波幅值随着拉应力的增加呈下降趋势,这是因为拉应力使微裂纹的两个裂纹面产生初始间隙,拉应力越大,初始间隙越大,SH0波与微裂纹作用时,裂纹面周期性的接触非线性效应减弱,从而抑制了二次谐波的产生．当拉应力足够大时,激励波的幅值大小无法克服此时拉应力产生的裂纹面间隙,因此不会出现接触声非线性效应,即不会产生二次谐波．

图8 单轴拉伸状态下不同微裂纹取向时的切向位移二次谐波归一化散射场Fig. 8 Normalized scattering fields of the 2nd harmonics under uniaxial tension for different microcrack orientations

上述现象可以通过提取非线性散射场中两个主瓣方向响应点的二次谐波幅值与拉应力之间的关系曲线来进一步说明．如图9所示,以40°和60°微裂纹模型为例,随着拉应力值增加,二次谐波的幅值单调递减．随着拉应力进一步增大,二次谐波幅值为零,即出现明显的阈值效应,原因在于当SH0波的最大幅值小于该拉应力值产生的最小裂纹面间隙,将不会产生接触声非线性效应．

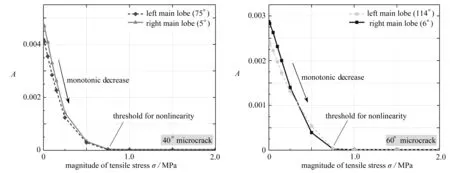
(a) 40°微裂纹 (b) 60°微裂纹(a) For the 40° microcrack (b) For the 60° microcrack图9 主瓣方向的二次谐波幅值与拉应力的关系曲线Fig. 9 Relationships between the 2nd harmonic amplitude and the tensile stress in the direction of the main lobe

图10为单轴压缩状态下的SH0波与不同角度微裂纹作用的切向位移二次谐波归一化非线性散射场．可以观察到,和单轴拉伸情况一样,压应力也不会破坏非线性散射场的指向性和对称性,仍然可以通过散射场的对称性来对微裂纹的取向进行判断．此外,压应力会对二次谐波的幅值产生显著的影响,但是影响规律和拉应力有所不同．

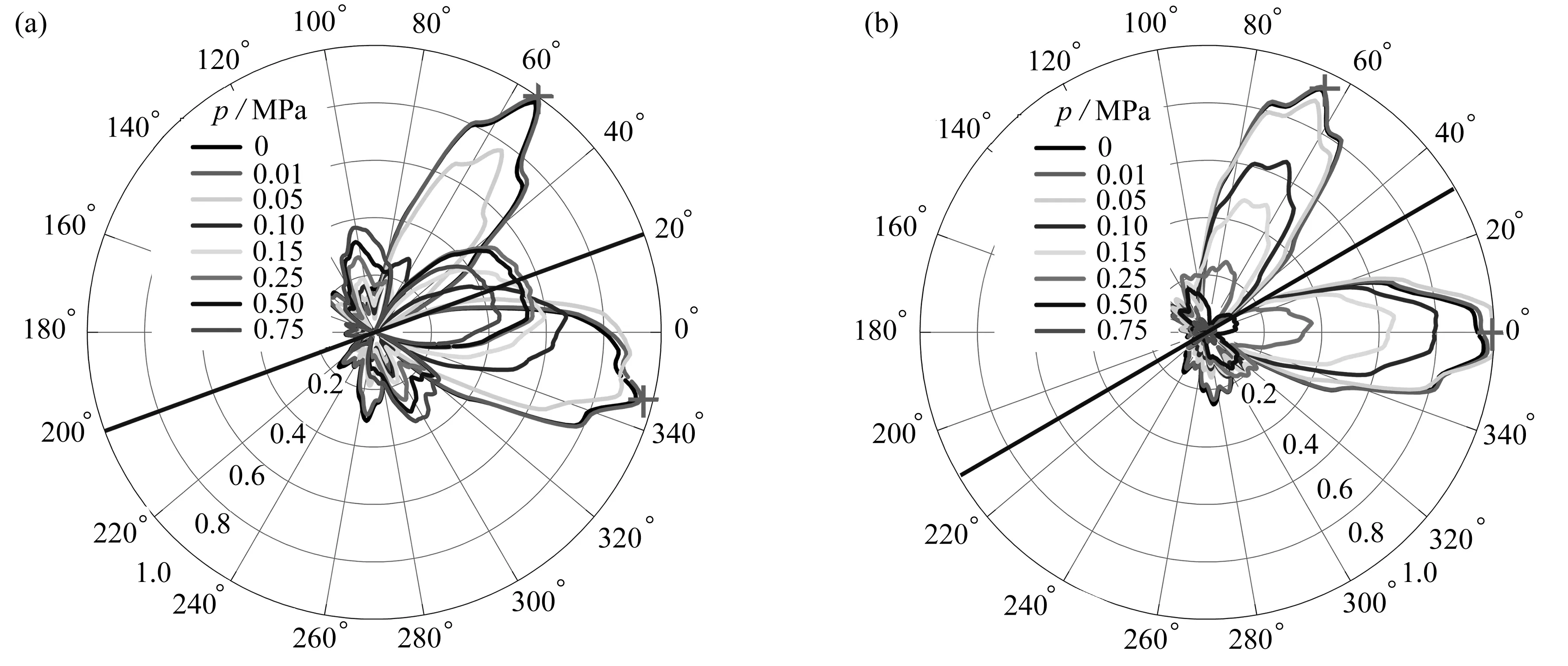
图10 单轴压缩状态下不同微裂纹取向对应的切向位移二次谐波归一化散射场Fig. 10 Normalized scattering fields of the 2nd harmonics under uniaxial compression for different microcrack orientations

如图11所示,仍然以40°和60°微裂纹为例,分别绘制非线性散射场中两个主瓣方向响应点的二次谐波幅值与预压应力的关系曲线．从图中可以看到,当压应力值增长处于较小范围内时,二次谐波幅值随压应力增大而增大．随着压应力继续增大,二次谐波幅值开始出现下降的趋势,这是因为压应力增大使得在裂纹面产生的接触应力增大,因而当SH0波与微裂纹作用时,接触声非线性效应逐渐减弱,从而使二次谐波滋生受到抑制．当压应力值进一步增大,SH0波的应力分量无法克服接触应力,此时不再产生接触声非线性效应,二次谐波幅值变为零．总之,二次谐波幅值随着压应力的增加呈先增加后减小最后保持为零的变化趋势,这一现象与二次谐波幅值随拉应力的变化趋势明显不同．

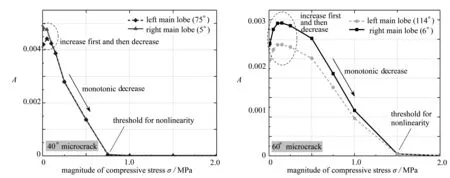
(a) 40°微裂纹 (b) 60°微裂纹(a) For the 40° microcrack (b) For the 60° microcrack图11 主瓣方向的二次谐波幅值与压应力的关系曲线Fig. 11 Relationships between the 2nd harmonic amplitude and the compressive stress in the direction of the main lobe

3 结 论

本文针对SH0波与微裂纹作用的非线性散射场问题,发展了一种数值方法来处理此类问题．该方法结合了处理有限元/谱单元耦合界面的mortar方法和计算接触摩擦问题的双势理论．利用mortar方法在处理非协调区域问题上的优势,分别采用有限单元和谱单元来离散内部的裂纹区域和外部的均匀区域,从而可以充分利用有限单元离散复杂结构的优势和谱单元计算效率高的优点．在求解不同角度裂纹模型的散射场时,只需要将外部区域固定,对裂纹区域进行整体旋转,该策略可以极大地简化裂纹建模流程,提升建模效率,同时还保证了计算不同裂纹模型时网格的一致性．提出了一种预处理半显式算法,该算法囊括了包含附加界面力的局部接触力的隐式求解和全局位移的显式求解,其可以在保证计算效率的同时不牺牲数值精度．本文的主要结论如下:

1) SH0波与微裂纹作用后的二次谐波散射场可以用于反演裂纹的取向．单轴预应力不会改变二次谐波散射场的指向性．

2) 非线性散射场中二次谐波的幅值会随着预拉应力或预压应力的变化而敏感变化．当结构受拉时,二次谐波幅值随拉应力增大而单调递减;当结构受压时,二次谐波幅值随压应力增大而先增加后减小．无论何种应力状态,当应力过大时,均会出现阈值现象,超过该阈值后将不再产生非线性效应．