耗散耦合腔磁系统中极化子的量子特性

李欣悦, 欧孝飞, 董婷婷, 佟雨潞, 朱爱东

( 延边大学 理学院, 吉林 延吉 133002 )

0 引言

由于钇铁石榴石(yttrium iron garnet,YIG)具有较高的自旋密度和较低的阻尼率,易于实现不同模式之间的强耦合(甚至超强耦合),因此其适合作为量子信息的载体,同时其也为研究量子的纠缠[1]、压缩[2]、双稳[3]和阻塞[4]等非经典效应提供了一个新的平台.2018年,Harder等[5]发现了一种由腔楞次效应引起的耗散磁振子-光子耦合现象,并提出了一种控制相干和耗散磁振子-光子耦合的方法;Xu等[6]从控制耦合机制的角度研究了由腔介导的2个磁子之间的远距离相互作用,并研究了2个钇铁石榴石球在腔中不同位置(分别对应于相干耦合或耗散耦合)时磁振子和腔模之间的间接耦合强度与频率失谐的关系.Wang等[7]和Guan等[8]分别提出了一种磁振子与光子之间通过热库发生间接耦合的方案.受以上研究的启发,本文构建了一个包含光子和磁振子模的非厄米腔磁系统,并研究了相干耦合、耗散耦合以及不同相位对哈密顿本征能谱的影响.

1 系统模型与哈密顿量

图1为系统模型的示意图.其中:左图为磁振子与微波腔组成的腔磁学系统的物理模型,该系统的微波电路可以同时支持驻波(相干耦合)和行波(耗散耦合),且通过改变YIG球的位置可以调节系统的耗散耦合和相干耦合强度.右图是系统内部相互作用的示意图,它表示微波腔模与磁振子模通过一个共同热库发生间接耗散耦合.本文将系统置于温度为20 mK的均匀磁场中,并将微波腔的外部耗散率设置为远大于其固有阻尼率.

图1 系统模型示意图

当腔模和磁振子模之间只存在相干耦合时,系统的哈密顿量可表示为:

H/ћ=ωca†a+ωmb†b+J(a+a†)(b+b†).

(1)

其中:a†和b†(a和b)分别是频率ωc的腔模和频率ωm的磁振子模的产生(湮灭)算符;J为腔模和磁振子模之间的相干耦合强度;磁振子频率ωm由外部偏置磁场B和旋磁比γ0调控,即ωm=γ0B.在旋波近似下,即当ωc,ωm≫J,κ,γ时,式(1)可以写为:

HRWA/ћ=ωca†a+ωmb†b+J(a†b+ab†).

(2)

当考虑腔模和磁振子模的集体耗散时,系统的演化可用如下的Lindblad主方程来描述:

(3)

其中:L[s]为标准耗散超算子,L[s]ρ=2sρs†-s†sρ-ρs†s,s={a,b,c};第2项描述的是腔模和磁振子模以η的速率集体耗散到行波中;第3项和第4项分别表示腔模和磁振子模的固有阻尼(阻尼率分别为α和β);c为腔算符和磁子算符的叠加算符(跳跃算符).为了描述不同方向微波场的驱动作用,本文引入相位θ表示不同端口的输入.不失一般性,当微波分别从端口1和端口2加载时,相干耦合和耗散耦合之间的相对相位θ分别为0和π.当微波驱动场分别从端口1和端口2加载时,跳跃算符c可表示为:

c≡λa±ξb,

(4)

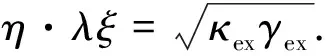
系统的动力学行为可以用如下量子朗之万方程描述:

(5)

(6)

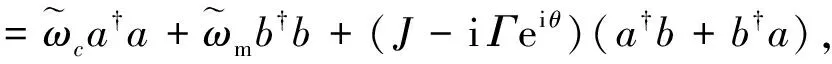
(7)

H=-iαa†a-Δmb†b+(J-iΓeiθ)(a†b+b†a),

(8)

式中Δm是磁振子频率与腔模之间的频率失谐,即Δm=ωm-ωc.式(8)中的哈密顿可表示为如下矩阵形式:

(9)

由式(9)可知,在系统中引入耗散耦合后可使原来的厄米系统变为PT对称的非厄米体系.于是由薛定谔方程可以得式(9)中哈密顿量的本征值为:

(10)

式(10)中,实部和虚部分别表示腔磁极化子的本征频率和耗散频率.

2 讨论与分析

2.1 相干耦合和耗散耦合对腔磁极化子的影响

在不同耗散耦合强度Γ和相干耦合强度J的条件下,哈密顿本征值的实部和虚部与磁振子频率失谐Δm的关系见图2—图7.图中的参数值分别取α/(2π)=1 MHz,β/(2π)=1 MHz,θ=0.

图2和图3为纯相干耦合机制下本征值的实部和虚部与频率失谐之间的关系,图中取J/(2π)=6 MHz,Γ/(2π)=0 MHz,其他参数的取值与上文所述的参数取值相同.由图2和图3可以看出,在只有相干耦合的情况下,系统本征值的实部发生了能级排斥现象,而虚部不发生劈裂.

图2 相干耦合机制下本征值实部与频率失谐的关系 图3 相干耦合机制下本征值虚部与频率失谐的关系

图4和图5为在只存在耗散耦合情况下本征值的实部和虚部与频率失谐Δm之间的关系,图中取Γ/(2π)= 6 MHz.当J= 0和θ= π时,由式(10)可得系统的本征值为:

(11)

图4 耗散耦合机制下本征值实部随失谐量的变化 图5 耗散耦合机制下本征值虚部随失谐量的变化

图6和图7为在相干耦合和耗散耦合的协同作用机制下本征值的实部和虚部与频率失谐之间的关系.由图6和图7可以看出,在耗散耦合和相干耦合的协同作用机制下,系统本征值的实部再次发生能级排斥的现象(与只有相干耦合时的能级状态相同).这说明,相干耦合在极化子的能谱分布中起主导作用.由图6还可以看出,在耗散耦合和相干耦合的协同作用下,虚部的能级排斥超出了图5中的异常点之间的范围,这说明当极化子处于2个不同本征态时其具有不同的耗散率.

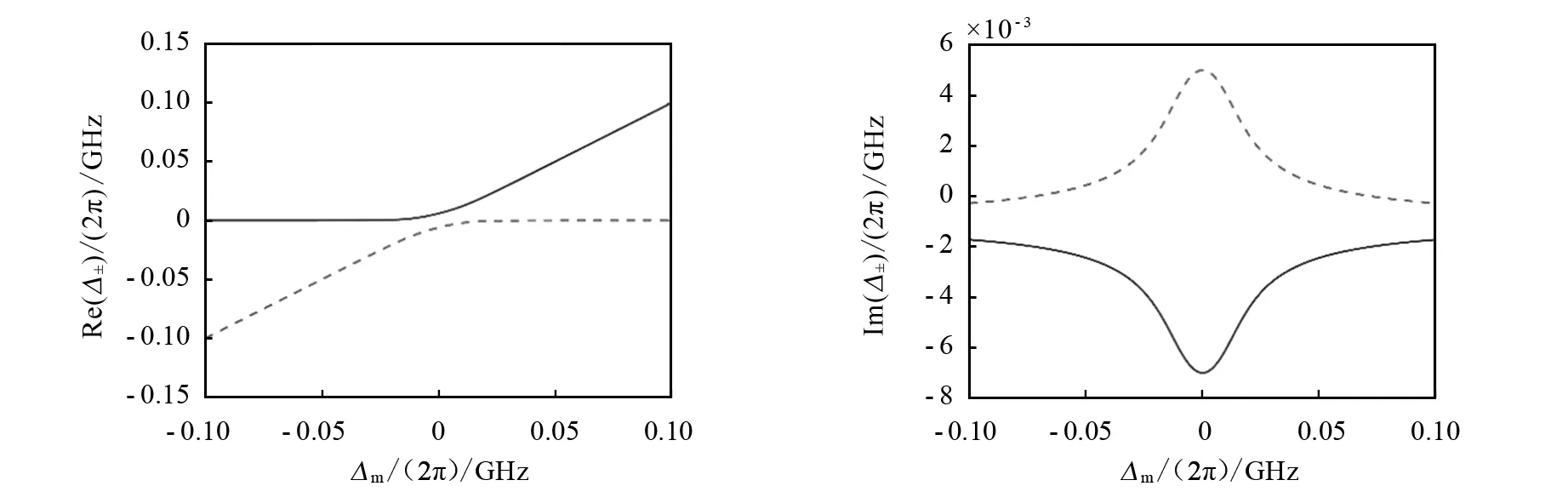
图6 在相干耦合和耗散耦合的协同作用机制下本征值实部与频率失谐的关系 图7 在相干耦合和耗散耦合的协同作用机制下本征值虚部与频率失谐的关系

2.2 相位对腔磁极化子的影响

图8为耗散机制下本征值的实部随相位的变化,其中左图中的磁振子失谐量取Δm/(2π)=10 MHz,右图中的磁振子失谐量取Δm/(2π)=30 MHz.由图8可以看出:本征值的实部随不同相位呈周期性变化;当调节磁振子失谐量时,本征值表现出周期性的能级吸引和排斥现象.

3 结论

本文在含有光子和磁振子的非厄米腔磁系统中研究了相干耦合和耗散耦合以及不同相位对腔磁极化子的影响.研究表明,相干耦合在此系统中起主导作用,且本征能谱随相位的变化呈周期性变化,即可以通过调节相干耦合和耗散耦合系数以及相位实现对腔磁极化子状态的操控.此外,在本征能谱的异常点两侧,能级呈不同分布,这表明在异常点附近出现了不同的量子行为.本文的研究结果可为研究腔磁纠缠、量子单向导引等非经典效应提供良好的理论参考.

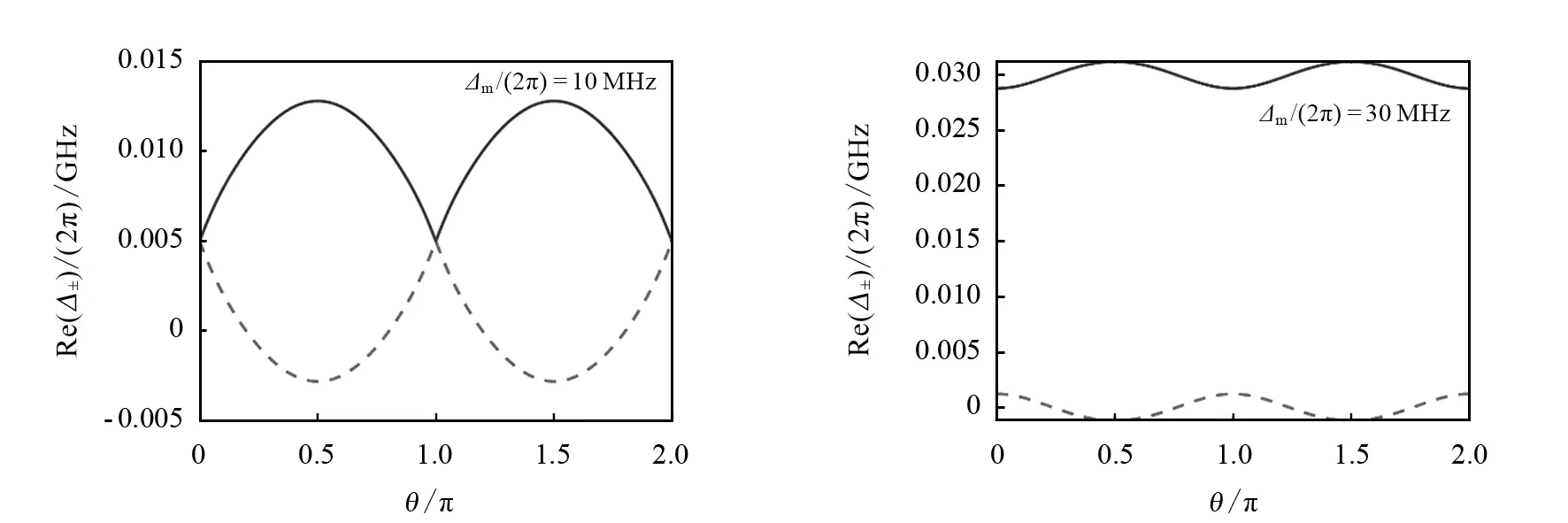
图8 耗散机制下本征值实部与相位的关系