基于改进BI-RRT算法的AGV路径规划

敖国鑫 李林

摘  要： 针对双向快速扩展随机树（BI-RRT）算法在路径规划中存在收敛速度慢、路径绕远、转折点多等问题，提出一种改进的BI-RRT算法。首先引入可变权重系数实现目标导向的同时又能較快的避开障碍物；然后对生成路径作基于障碍物判断策略的剪枝优化；最后用三次B样条曲线进行平滑处理，并提出“优化域”概念解决路径碰撞障碍物问题。仿真结果表明，本文改进后的算法收敛速度更快、路径更加平滑、长度减少。

关键词： 路径规划； BI

0 引言

近年来，自动导引车AGV以其高自动化和便捷性在工业生产中得到广泛应用。优秀的路径规划算法对AGV的工作效率有着重要影响。传统的路径规划算法主要有基于搜索和采样两大类。基于搜索的一般有蚁群算法[1]、A-star[2]、遗传算法[3]等，基于采样的有概率线路图算法（PRM）[4]、快速拓展随机树（RRT）[5]等。其中，RRT算法无需对空间障碍物进行预处理、搜索速度快，在相对复杂的空间有比较广泛的应用[6]。但是RRT算法也有其不足之处，如绕路现象严重，随机盲目性强、易陷入局部最优等[7]。

针对RRT算法存在的问题，国内外很多学者作了大量研究，提出了不同的方法来改进。Kuffner Jr[8]等人提出双向生长随机树（Bi-RRT）算法，即在起点和终点同时扩展两棵搜索树，减少了路径规划的时间；阮晓钢[9]等人提出基于子目标搜索的目标导向算法，减少了RRT算法的冗余搜索；李磊[10]等在BI-RRT算法中引入贪婪算法思想，使得树尽可能朝目标点生长，大大缩短了路径长度；孙钦鹏等提出可变步长的方法，优化新节点的选择方式，实现了在复杂环境下的路径优化。除了对算法本身的研究，也有不少学者将RRT算法与其他算法融合进行改进，施杨洋[12]等将人工势场法的目标引力思想引入RRT算法的节点扩展中，减少了树的随机性；王雨[13]等对RRT算法规划出的路径利用三次B样条曲线作平滑处理，增加路径的连续性。

针对BI-RRT算法存在的强随机性、算法收敛速度慢、路径拐点多的问题，本文提出相应的改进优化方法。首先，引入可变权重系数，保证目标导向能力的同时优化避障能力；然后，对生成路径作剪枝优化来剔除冗余点，减少路径长度。最后，对剪枝后的路径用3次B样条曲线作平滑处理，针对3次B样条曲线平滑后的路径存在碰撞障碍物的情况，提出“优化域”概念，增加路径的平滑性和连贯性。通过MATLAB对本文算法进行仿真，验证算法的有效性。

1 基本BI-RRT算法

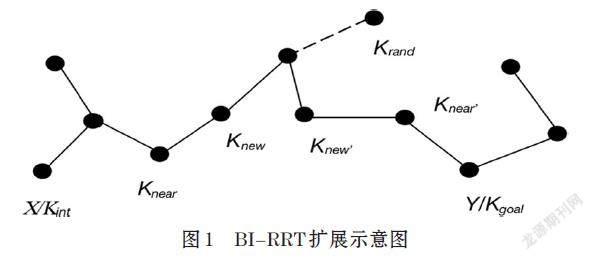
RRT算法以起点Kint为根节点定义一颗随机树，通过提前给定的约束条件在状态空间内进行随机树的扩展。双向快速拓展随机树（BI-RRT）相较于RRT算法，在节点拓展策略上引入双树拓展的环节，在起点和终点分别定义随机树X和随机树Y，随机树X以Kgoal为目标点作随机生长，随机树Y以Kint为目标点作随机生长，d为每次生长的步长。通过一次采样得到随机树X的随机点Krand，找到距Krand欧氏距离最小点Knear，朝Krand方向生长步长d得到新节点Knew，然后检测Knew是否碰撞到障碍物，若是，则将这个采样点舍去，若不是，则将Knew添加到随机树中。随机树Y也执行此操作，两颗搜索树交替进行扩展，直到检测到两棵树的新节点的欧氏距离小于设定的阀值或者相遇时，便连接两个点生成随机树，路径也由此生成。

BI-RRT扩展示意图如图1所示。BI-RRT算法也存在一些缺点：随机树的扩展是基于随机采样点的，采样点的随机性和偏差性导致两棵树难以连接，算法收敛速度较低。算法的无方向性，容易陷入局部极小值问题，生成大量不必要的节点进而发生绕远现象。生成的路径转折较大、连贯性不足。

2 改进Bi-RRT算法

2.1 可变权重系数

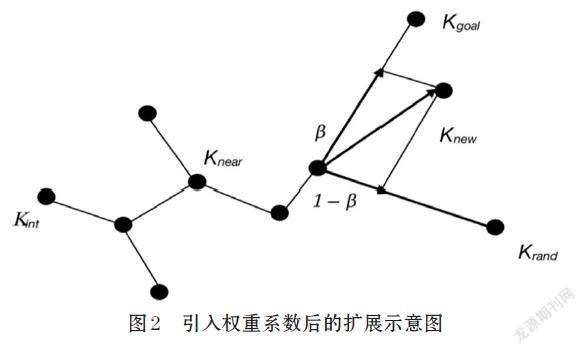
原本的RRT算法由于没有融入目标节点的导向思想，节点随机生成，导致了随机树的无向扩展且有大量的冗余节点，降低了算法收敛速度和路径质量。针对随机树的无方向性，部分研究提出引入固定目标偏置权重系数，核心思想是在目标点和随机点两个方向取固定权重系数P1和P2，通过仿真来确定系数之后再做矢量计算来确定随机树的拓展方向。该方法改变传统RRT算法随机树生长的无方向性，使得节点生长的同时逐渐向目标节点靠近，但是这一方法在复杂环境（如迷宫环境）下容易陷入局部最优产生大量无效节点。因此，针对这一问题，本文引入可变导向系数目标偏向策略，即在目标点方向和随机点方向加入互相牵制的权重系数[β]和[1-β]，加入可变权重系数之后，新节点[Knew]的生成方式采用以下公式确定：

[Knew=Knear+β（Kgoal-Knear）Kgoal-Knear+（1-β）（Krand-Knear）Krand-Knear] ⑴

其中，[β]（0<[β]<1）代表权重系数，当[β]>0.5时，[Knew]将偏向于目标点方向；当[β]<0.5时，[Knew]将偏向于随机方向引入可变权重系数之后，系数的选取影响着新节点[Knew]的确定。在搜索过程中，根据障碍物信息不断调整[β]值大小，当[Knew]与[Knear]的连线上没有检测到障碍物碰撞时，选取 [β ]>0.5，此时新节点将偏向目标点方向；反之，当出现障碍物碰撞时，选取[ β ]<0.5，新节点将偏向随机点方向，此时的RRT算法与传统的RRT算法相似，具有较强的避障能力和随机性。如图2所示，权重系数[β]的调整实现了算法法目标导向的同时又保持了RRT算法本身的避障能力。

2.2 基于障碍物判断的剪枝策略

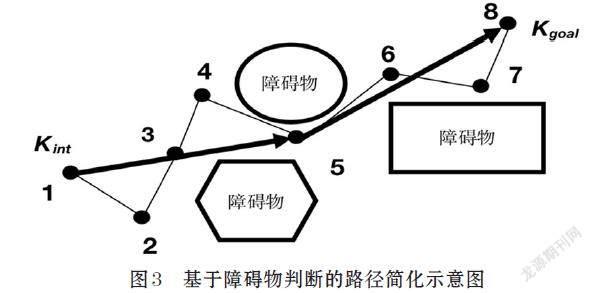
经上述优化之后，BI-RRT算法的收敛速度、路径质量得到提高，但是生成的路径依然有较多的冗余节点，冗余节点会导致AGV的运行出现绕远现象。对此，本文提出基于障碍物判断的剪枝策略，对路径进行剪枝处理（见图3），具体实施策略解释如下：

⑴ 提取路径节点。在初始路径上从起始节点到目标节点按顺序依次记为Cn（n=1，2，3…n），C1为起始节点首先加入到路径节点列表path_tree（）中。

⑵ 障碍物判断。依次判断起始节点C1与路径节点Cn之间的直线路径上是否存在障碍物。

⑶ 对障碍物判断结果进行处理。判断结果分为两种情况。情形一，如果起始点与节点Cn的直线路径上检测到障碍物，则无需对节点Cn后面的节点进行障碍物判断，剔除C1与Cn-1之间的节点，连接起始点C1和Cn-1生成一条路径，将Cn-1作为作为新的起始点，进行新的障碍物判断操作。

⑷ 情形二，如果障碍物判断一直到目标点都没有检测到障碍物，则直接连接起始点与目标点生成最终路径。

2.3 三次B样条曲线优化

AGV能够平稳运行的前提是路线平滑，过多的转折点不仅会增加AGV工作时间，还会增加能量消耗。当AGV运行到转弯节点时通常需要停下来、转弯、起步、加速的动作，这些动作增加了AGV运行时间、降低了运行效率。为了让AGV能够在规划出来的路径上平稳运行，本文用三次B样条曲线对改进后的路径进行拟合。3次B样条曲线表达式为：

[Pis=j=103Bj，3（s）Ci+j]  ⑵

其中，s为参数，[s∈0，1，Bj，3（s）]为三次B样条基函数；[Ci+j]为第[i]段中的第[j]个控制点。

3次B样条的基本函数的矩阵形式为：

[Bj，3s=16s3s2  s  1G]  ⑶

其中，

[G=13-313-630-30301410]

代入式⑶，可求得三次B樣条曲线的基函数：

[b0=16-k3+3k2-3k+1b1=163k2-6k+4b2=16（-3k3+6k2+3k+1）b3=16k3]

其中，k表示节点，[b0]、[b1]、[b2]、[b3]表示基函数。

但是，在复杂障碍物情况下，若直接采用三次B样条曲线作路径平滑处理，容易出现平滑出的路径穿过障碍物的情况，如图4所示。

为了避免AGV碰撞障碍物的情况发生，本文提出“优化域”概念，即在转折点前后相同距离处设置两个端点，端点离转折点的距离值根据实际情况调节。如图5所示，设置M1，M3端点，[M1M2=M2M3]，这两个端点形成的区域就是三次B样条曲线的优化区域，在优化域内进行平滑优化，这样就避免了平滑出的路线相较于原始路线出现太大的变化导致路径穿过障碍物的情况。

3 算法仿真与验证

为了验证改进后的BI-RRT算法有更好的性能和效率，通过仿真将改进算法与其他RRT相关的算法做对比分析，仿真硬件为MacBookAir（M1，2020），计算机配置：8GB统一内存，256GB固态硬盘，M1芯片，8核CPU，macOSMonterey 12.5系统。

3.1 二维仿真分析

由于BI-RRT算法在路径规划时存在随机性，因此建立三种不同类型的地图（简单环境，复杂障碍物环境、迷宫环境），在三种类型地图中分别对RRT，BI-RRT和本文改进后的BI-RRT算法进行实验，地图大小为500*500，起点坐标为（10，10），终点坐标为（490，490），每次拓展步长d=20，最大节点数量为3000，每种算法各在三种类型的地图下运行50次，记录每次运行的数据。

从图6～图8可以看出，在三种不同类型的障碍物环境下，从路径质量来看，本文改进的BI-RRT算法规划出来的路径更符合AGV运行，主要表现为转弯次数明显减少，路径更加平滑。表1～表3是三种障碍物环境下50次仿真实验记录的各项数据的平均值。

在地图1的环境下，障碍物分布比较稀疏。由表1可知，本文改进的BI-RRT算法相比于RRT算法，在平均采样点数上减少52.4%，平均路径长度减少24.9%，平均规划时间减少59.2%；相较于BI-RRT，均采样点数上减少45.4%，平均路径长度减少17.4%，平均规划时间减少26.1%。

在地图2的地图环境下，地图障碍物分布比较密集，通道比较狭窄。由表2可知，本文改进的BI-RRT算法相比于RRT算法，在平均采样点数上减少43.6%，平均路径长度减少19.4%，平均规划时间减少52%；与BI-RRT相比，均采样点数减少37.9%，平均路径长度减少14.5%，平均规划时间减少34.4%。

在地图3的地图环境下，障碍物呈迷宫状，有多个复杂空间和陷阱区域，算法易在复杂区域震荡而无法收敛。由表3可知，本文改进的BI-RRT算法相比于RRT算法，在平均采样点数上减少36.7%，平均路径长度减少30%，平均规划时间减少58.2%；相较于BI-RRT，均采样点数上减少30%，平均路径长度减少25.2%，平均规划时间减少30%。

4 结束语

本文针对双向RRT算法的缺点：随机性强、收敛速度慢、路径不连续等问题，提出一种基于双向RRT算法改进的AGV路径规划。在BI-RRT算法的基础上引入可变权重系数，实现目标导向和避障能力的优化，同时提高了算法收敛速度；对生成路径作剪枝优化剔除冗余点，缩短路径长度；对优化后的路径用3次B样条曲线作平滑处理，增加路径的平滑性和连贯性，针对路径碰撞障碍物问题，提出“优化域”概念，实现避障。MATLAB仿真数据表明，本文改进的算法在平均采样点数、平均路径长度及平均规划时间三个维度上都有明显的降低，规划出来的路径连续性更强、转角更小，证明了本文算法的优越性和实用性。

参考文献（References）：

[1] 王明辉.基于改进多步长蚁群算法的机器人路径规划[J].机床与液压，2022，50（15）：43-46

[2] 沈克宇，游志宇，刘永鑫，等.基于改进A*算法的移动机器人路径规划[J].计算机应用研究，2022，8：1-6

[3] 杨博，刘树东，鲁维佳，等.改进遗传算法在机器人路径规划中的应用[J].现代制造工程，2022（6）：9-16

[4] 李琼琼，徐溢琪，布升强，等.基于修正PRM算法的智能车辆路径规划研究[J].森林工程，2022（5）：179-186

[5] 陈法法，蒋浩，李振，等.基于改进RRT的智能巡检机器人狭窄通道路径规划[J].组合机床与自动化加工技术，2022（10）：40-45

[6] 张卫波，肖继亮.改进RRT算法在复杂环境下智能车路径规划中的应用[J].中国公路学报，2021，34（3）：225-234

[7] 李扬，张蕾，李鹏飞，等.基于改进RRT结合B样条的机械臂运动规划方法[J].计算机集成制造系统，2022，10：1-17

[8] LAVALLE S M，KUFFNER J.Randomized kinodynamicplanning[J].The International Journal of Robotics and Research，1999，15（5）：378－400

[9] 阮晓钢，周静，张晶晶，等.基于子目标搜索的机器人目标导向RRT路径规划算法[J].控制与决策，2020，35（10）：2543-2548

[10] 李磊，吴翔，包祥威，等.基于改进RRT-Connect算法的机械臂抓取路径规划[J].机器人技术与应用，2021（2）：28-32

[11] 孙钦鹏，李猛，王中华.基于改进快速扩展随机树算法的移动机器人路径规划[J].济南大学学报（自然科学版），2019，33（5）：431-438

[12] 施杨洋，杨家富，布升强，等.基于RRT改进的智能车辆路径规划算法[J].计算技术与自动化，2019，38（4）：81-86

[13] 王雨，刘延俊，贾华，等.基于强化RRT算法的机械臂路径规划[J].山东大学学报（工学版），2022：1-9-RRT； 可变权重系数； 剪枝； 三次B样条