改进遗传算法求解旅行商问题

刘树赵 邹德旋 罗鸿赟 张慧峰 李梦迪

摘  要： 针对传统遗传算法求解旅行商问题收敛速度慢且不稳定的问题，提出了一种改进遗传算法（Improved genetic algorithms， IGA）。通过邻域搜索算法对初始化种群进行优化；设计了一种自适应调节的交叉和变异概率；加入了Metropolis准则，以一定概率接受劣解，提高跳出局部最优的能力；加入了逆转操作加强局部搜索能力，加快种群收敛。利用Matlab将IGA和其他五种算法在TSPLIB数据库中进行试验，结果表明，该算法在中小型TSP问题上的收敛速度和求解精度都有一定的优势。

关键词： 遗传算法； 旅行商问题； 领域搜索算法； 自适应调节

中图分类号：TP301.6          文献标识码：A     文章编号：1006-8228（2023）05-66-06

Improved genetic algorithm to solve traveling salesman problem

Liu Shuzhao， Zou Dexuan， Luo Hongyun， Zhang Huifeng， Li Mengdi

（School of Electrical Engineering and automation， Jiangsu Normal University， Xuzhou， Jiangsu 221116， China）

Abstract： Aiming at the slow and unstable convergence of the traditional genetic algorithm for solving the travelling salesman problem （TSP）， an improved genetic algorithm （IGA） is proposed. The initialized population is optimized by the neighborhood search algorithm. An adaptive adjustment of crossover and variation probability is designed. The Metropolis criterion is added to accept inferior solutions with a certain probability， which improves the ability to jump out of the local optimum. The reversal operation is added to strengthen local search capabilities and accelerate population convergence. The IGA and other five algorithms are tested in the TSPLIB database using Matlab， and the results show that the convergence speed and solution accuracy of the algorithm have certain advantages in small and medium-sized TSP problems.

Key words： genetic algorithm; the travelling salesman problem （TSP）; domain search algorithm; adaptive adjustment

0 引言

旅行商問题（TSP）是组合优化领域很经典的一个NP-Hard问题[1]，可以简单描述为一个商人在已知的城市中不重复的访问每一个城市，最后回到出发的城市，商人的路线便是旅行商问题的解。该问题具有广泛的工程应用背景，如网络通信接点的设置、物流路径规划、飞机航线的安排等[2]。目前，很多智能优化算法应用于求解TSP问题，主要有遗传算法（GA）[3]、粒子群算法（PSO）[4]、蚁群算法（ACO）[5]、模拟退火算法（SA）[6]以及人工萤火虫优化算法（AGSO）[7]等，并且都取得了不错的效果。

Holland教授于1975年首先提出了遗传算法[8]。遗传算法作为一种启发式随机搜索算法，通用性强，目前已经有很多学者从不同方面对遗传算法进行改进，来解决TSP问题，并取得了不错的效果。如刘艳琪等人[9]提出了基于病毒侵染的改进遗传算法，通过加入病毒种群来感染初始种群，加快了算法的收敛速度；徐佳等人[10]提出了一种生物信息启发式遗传算法，引入生物学中的基因序列对比手法改进交叉操作，获得较为稳定的求解结果；于莹莹等人[11]提出了基于贪婪操作的启发式交叉算子，使算法具有更可靠的寻有能力；王震等人[12]通过贪婪算法初始化种群，变异算子采用2-opt局部优化算法，可以使算法在较小的迭代次数内得到质量更高的全局最优解；姚宇威等人[13]将杂草算法和遗传算法混合，在解决算法易陷入局部最优这一缺陷上有明显的改善；李庆等人[14]通过设计了一个动态适应度函数以及引入了相似度概念，使得遗传算法在优化性能上获得了较大提升。

基于以上分析，本文提出了一种改进遗传算法（IGA），在种群初始化的过程中引入了邻域搜索算法优化种群，使得算法在迭代初期就有较好的种群；设计了自适应调节的交叉和变异概率，平衡了算法的全局和局部搜索能力；引入了Metropolis准则，以一定概率接受劣解，提高跳出局部最优的能力；最后通过加入逆转操作，加快算法的收敛。

1 TSP问题

TSP问题可以抽象描述为在一个带权重的完全无向图中，找到一个权值总和最小的哈密顿回路。其数学模型为，要在给出的城市中找到一条最优路径：[V=v1，v2，…vn]，并满足提下目标函数：

[LV=mini=1n-1d（vi，vi+1）+dvn，v1]  ⑴

其中，[vi]为城市编号，[dvi，vi+1]为城市[vi]到[vi+1]的距离，[n]为城市总数，[1≤i≤n]。

2 传统遗传算法

传统遗传算法基本步驟：

step 1 确定合适的编码方式，对种群进行初始化。

step 2 建立合适的适应度函数，并计算生成的种群中个体的适应度值。

step 3 根据个体适应度值进行选择操作，主要的选择方式有轮盘赌选择法和锦标赛选择法等。

step 4 根据交叉概率进行交叉操作，生成新的种群。

step 5 根据变异概率进行变异操作，生成新的种群。

step 6 判断是否满足停止条件，如果满足，则输出结果；如果不满足，则转到step2。

尽管传统遗传算法已经具备不错的全局寻优能力和全局收敛能力，但在处理复杂问题时，效率较低，为了追求更高的精度以及更快的收敛速度，本文提出一种改进遗传算法，用于求解TSP问题。

3 改进遗传算法

3.1 种群初始化

传统遗传算法的种群初始化通常是由计算机随机生成，这样容易使初始种群的个体适应度与我们想要求得的最优适应度偏差较大，从而使算法收敛速度较慢且运行耗时较高，导致解的质量的下降。因此，IGA中采用邻域搜索算法生成种群与随机生成种群相结合，一半种群由邻域搜索生成，另一半种群由计算机随机生成，在提高初始种群质量的同时，又保证了初始种群的多样性，在提高种群初期收敛速度的同时，又防止陷入局部最优。邻域搜索算法具体方法如下。

对所给的城市进行编码，得到序号集合[1，2，…，n]。随机生成起始城市[i]，在剩下的城市中找到一个与城市[i]距离最近的城市，构成路径，依次在剩下的城市中选择与上一个被选择的城市最短距离的城市，直到构成一条完整路径。这样得到的城市路径形成的初始种群，在一开始便有一个良好的适应度，对于算法的收敛和求解精度的提高都有一定的帮助。

3.2 自适应交叉和变异概率

传统的遗传算法一般使用固定的交叉和变异概率，这会导致优良个体被破坏以及劣质个体被保留，影响算法的性能。在本文中设计了一种自适应交叉和变异概率，根据当前个体的适应度值以及当前种群个体最大适应度与平均适应度的差值相结合自动调整交叉和变异概率，算法交叉概率[pc]和变异概率[pm]如下：

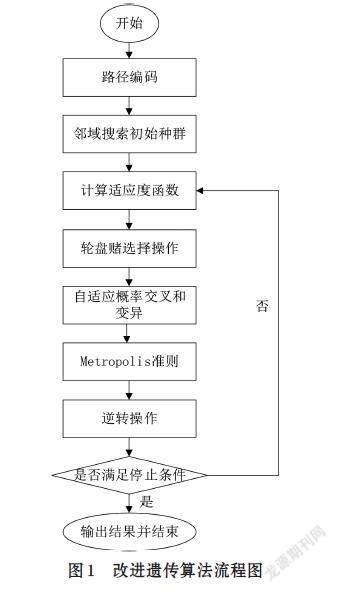
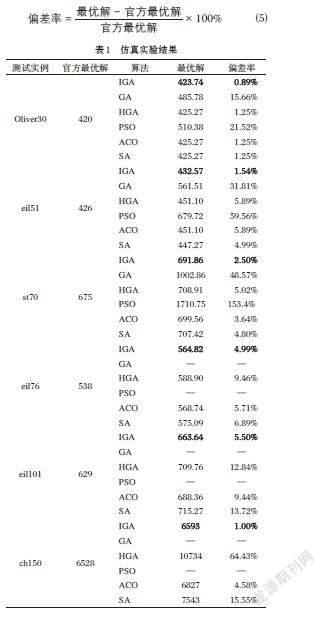
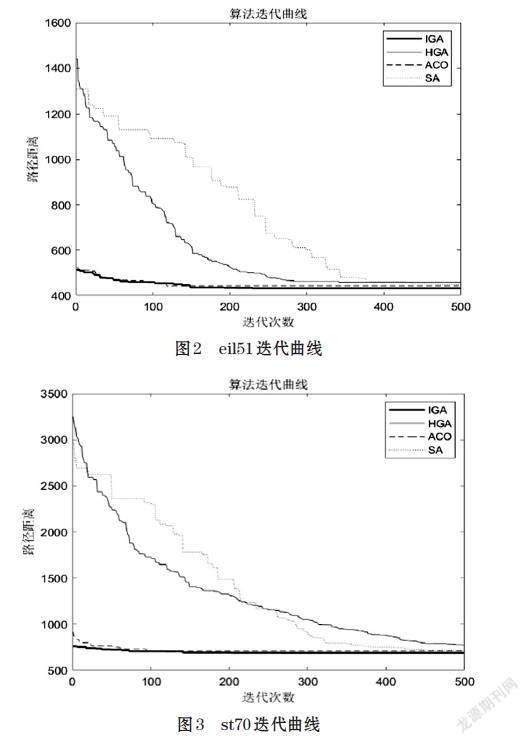
[pc=k1sin（fmax-f'fmax-f），   f'≥fk3                             ，          f'

[pm=k2sin（fmax-ffmax-f），            f≥fk4                            ，            f

其中，[k1]，[k2]，[k3]，[k4≤]1.0，[fmax]为当前种群中个体适应度最大值，[f]为当前种群个体适应度平均值，[f']为待交叉的两个个体中适应度大的值，[f]为待变异个体适应度值。

分析式⑵和式⑶，当[fmax-f]变小时，也就是说种群中个体适应度值最大值接近种群个体适应度平均值，这时候算法可能收敛到了全局最优解，也可能陷入了局部最优解，因此它的交叉概率[pc]和变异概率[pm]增大，增加种群的多样性；当[fmax-f]变大时，则相反。在某一代的种群中，不同的个体应该对应不同的[pc]和[pm]，做到尽可能的保留优质个体，淘汰劣质个体，因此，当个体适应度值大，降低该个体的[pc]和[pm]，当个体适应度值小，增大该个体的[pc]和[pm]。在公式中加入了三角函数，使交叉概率和变异概率呈非线性变化，易于算法跳出局部最优解。

3.3 加入Metropolis准则

传统遗传算法随机性强，但在算法进化的后期，仍然存在容易陷入局部最优导致算法收敛，所求解与最优解相差较大。而模拟退火算法具有良好的局部寻优能力，并且可以概率性的跳出局部最优并最终趋向于全局最优。Metropolis准则就是帮助模拟退火算法跳出局部最优的重要部分，因此，本文在传统遗传算法中加入了Metropolis准则帮助算法在迭代过程中跳出局部最优。具体方法如下。

当算法在变异操作后生成新的种群，对所生成的种群中每个解进行操作。随机选取解中的两个城市，并将这两个城市之间（包含这两个城市）所有的城市顺序随机打乱，如当前城市为：

A→B→C→D→E→F→G→H

随机选中的城市为C和F，那么打乱之后的顺序为：

A→B→E→C→F→D→G→H

计算原来路径长度的大小[distpast]以及新生成路径适应度值[distnew]的大小，比较[distnew]和[dist]的大小，如果[distnew]小于[distpast]，则用新路径代替原来的路径，如果[distnew]大于[distpast]，则以概率[p1]接收新路径。概率[p1]的数学表达式如下所示：

[p1=e-distnew-distpastmaxgen-0.9×gen]  ⑷

其中，[maxgen]为算法最大迭代次数，[gen]为算法当前迭代次数。随着算法迭代的进行，[maxgen-0.9×gen]在不断的减小，根据指数函数的特点，[p1]的值也在不断减小，算法接受劣解的概率减小，有助于算法整体收敛。并且当[distnew-distpast]的值较大时，也就是新解和旧解相差较大，[p1]的概率也在变小，接受劣解的概率减小，相反，当[distnew-distpast]的值较小时，接受劣解的概率增大，在不影响算法收敛能力的同时保留了跳出局部最优的能力。

3.4 逆转操作

传统遗传算法适应性强，适用于各种组合优化的问题，但在解决复杂问题时，收敛速度较慢，往往需要多次迭代才能寻得全局最优。为了解决这一缺陷，根据局部寻优的思想在算法中加入逆转操作，加快种群收敛，逆转操作具体方法如下所示：

经过上述操作后，在生成的种群中随机选取解的两个城市，并将这两个城市之间的顺序倒换，如当前城市为：

A→B→C→D→E→F→G→H

随机选中的城市为C和F，那么打乱之后的顺序为：

A→B→F→E→D→C→G→H

然后将路径距离更小的解保留。

3.5 改进自适应遗传算法求解TSP问题具体步骤

step 1 邻域搜索算法与随机生成相结合，初始化种群。

step 2 计算适应度函数。

step 3 采用轮盘赌选择法与精英保留策略结合，精英保留比为0.9。

step 4 改进OX交叉操作。操作如下：

父代1：

A→B→C→D→E→F→G→H

父代2：

B→A→E→F→C→H→G→D

随机选择起点和终点，如第3位和第5位;

父代1：

E→F→C→A→B→C→D→E→F→G→H

父代2：

B→A→E→F→C→H→G→D→C→D→E

根据映射关系消去路径中相同的城市;

父代1：

E→F→C→A→B→D→G→H

父代2：

B→A→F→H→G→C→D→E

改进的OX交叉算子，即使在要交叉的两个父代相同的情况下，也会生成不同的子代。

step 5 交换变异，操作如下：

在生成的路径中随机选两个城市，交换两个城市的位置，如当前城市为：

A→B→C→D→E→F→G→H

选择的城市为B和E，那么新路径为：

A→E→C→D→B→F→G→H

step 6 加入Metropolis准则，以一定概率接受劣解。

step 7 逆转操作。

step 8 判断是否满足停止条件，满足，则输出结果；不满足，则跳转到step 2。

本文改进遗传算法流程图如图1所示。

图1  改进遗传算法流程图

4 仿真实验

4.1 实验环境与参数设置

为了测试改进遗传算法的性能，将IGA与另外5种算法在Matlab仿真软件上对TSPLIB数据集不同城市规模的实例进行测试，5种算法分别为传统遗传算法（GA）、粒子群算法（PSO）、蚁群算法（ACO）、模拟退火算法（SA）以及结合2-opt局部寻优操作的混合遗传算法（HGA）。

所有的实验均处于同一环境下，即操作系统为Windows10，处理器为Intel?Core（TM）i5-7300HQ，8GRAM，运行环境为Matlab 2019a。传统遗传算法（GA）种群规模为100，最大迭代次数为1000，交叉概率为0.9，变异概率为0.05；粒子群算法（PSO）粒子数量为100，最大迭代次数为1000；蚁群算法（ACO）蚂蚁数量取100，信息素重要程度因子取1，启发函数重要因子取5，信息素挥发因子取0.1，最大迭代次数取500；模拟退火算法（SA）初始温度为100摄氏度，结束温度为0.66摄氏度，温度衰减系数为0.99，馬尔科夫链长度为500；混合遗传算法（HGA）种群规模为100，最大迭代次数为1000，交叉概率为0.9，变异概率为0.05；本文算法种群规模为100，最大迭代次数为500，[k1=k3=1.0]，[k2=k4=0.5]。

4.2 仿真结果分析

按照上述实验前的准备，将六个算法在六个TSPLIB实例上独立运行20次，记录每次的运行结果。找出最优解，并结合TSPLIB实例的已知最优解[15]，根据公式计算偏差率，具体公式如下：

六种算法具体实验结果见表1。由于传统遗传算法（GA）和粒子群算法（PSO）在求解规模稍大的TSP问题时偏差较大，求解的质量很差，所以舍弃一部分实验结果。从表1可知，相对于本文涉及到的其他几种算法，改进遗传算法（IGA）在中小型TSP问题的求解精度上更高，对于TSP问题的求解具有一定优势。

为了更加直观的了解上述算法求解TSP问题的具体过程，以IGA、HGA、ACO、SA为例，设置最大迭代次数都为500代，本文绘制了eil51、st70、eil76和eil101这四个具有代表性实例的迭代曲线，如图2～图5所示。通过观察这四分迭代曲线我们可以发现，本文的改进遗传算法（IGA）初始化种群采用了邻域搜索算法和随机生成相结合的方法，初始解便具有很大优势；采用了自适应交叉和变异概率以及加入了逆转操作，加快了算法的收敛；加入了Metropolis准则，以一定概率接受劣解，提高了跳出局部最优的能力，对算法的求解精度也有一定的提高。图6～图9给出了本文算法求解到的最优路径图。

5 结束语

本文提出了一种改进遗传算法（Improvegenetic algorithms，IGA）来解决旅行商问题。通过邻域搜索算法对初始化种群进行优化，也保留了随机生成种群策略，在提高初始种群质量的同时保证了种群多样性；设计了一种自适应调节的交叉和变异概率，提高算法寻优效率；加入了Metropolis准则，以一定概率接受劣解，提高跳出局部最优的能力；加入了逆转操作加强局部搜索能力，加快种群收敛。利用Matlab对IGA和其他五种算法对TSPLIB数据库中进行试验，实验结果表明，该算法在中小型TSP问题上的收敛速度、求解精度都有一定的优势。

参考文献（References）：

[1] 程荣.遗传算法求解旅行商问题[J].科技风，2017，（16）：40，51

[2] 高海昌，冯博琴，朱利.智能优化算法求解TSP问题[J].控制与决策，2006（3）：241-247，252

[3] 张占云，宗晓萍，王培光.基于旅行商问题的改进遗传算法研究[J].电子世界，2017（7）：19-21

[4] 罗金炎.一种求解旅行商问题的改進粒子群算法[J].沈阳化工大学学报，2017，31（4）：377-384

[5] 贾燕花.蚁群算法在旅行商问题（TSP）中的应用研究[J].计算机与数字工程，2016，44（9）：1664-1667

[6] 郭乐新.基于模拟退火算法的旅行商问题的实现[J].现代计算机（专业版），2012（3）：3-5，18

[7] 周永权，黄正新.求解TSP的人工萤火虫群优化算法[J].控制与决策，2012，27（12）：1816-1821

[8] HOLLAND J H. Adaptationin natural and artificialsystems：an introductory analysis with applications to biologycontrolandartificial intelligence[M].Massachusetts，USA：MIT press，1992

[9] 刘艳琪，刘一杰.基于病毒侵染和逆转操作的改进遗传算法[J].湖南文理学院学报（自然科学版），2022，34（3）：23-29

[10] 徐佳，韩逢庆，刘奇鑫，等.一种求解TSP的生物信息启发式遗传算法[J].系统仿真学报，2022，34（8）：1811-1819

[11] 于莹莹，陈燕，李桃迎.改进的遗传算法求解旅行商问题[J].控制与决策，2014，29（8）：1483-1488

[12] 王震，刘瑞敏，朱阳光，等.一种求解TSP问题的改进遗传算法[J].电子测量技术，2019，42（23）：91-96

[13] 姚宇威，邓燕妮.混合杂草遗传算法求解旅行商问题[J].科学技术创新，2020（11）：40-41

[14] 李庆，魏光村，高兰，等.用于求解TSP问题的遗传算法改进[J]. 软件导刊，2020，19（3）：116-119

[15] REINELT G.TSPLIB-A traveling salesman problemlibrary[J].OSRA Journal on Computing，1991，3（4）：376-384