角速率输入下的双子样二次迭代圆锥补偿算法

任雪佳，丁立波，冯 阳，路 坦

(1 南京理工大学机械工程学院，江苏 南京 210094；2 安徽湘凡科技有限公司，安徽 合肥 231200)

0 引言

捷联惯性导航具有结构简单、功耗低、可靠性高等优点,对于单兵弹药,考虑到低成本与高精度的要求,能够满足其导航需求。研究单兵弹药纯惯性导航的姿态解算,可以在较低成本下提高单兵作战的打击能力,具有较高的实际应用价值。

姿态更新解算作为捷联惯导系统的核心,已进行了大量的研究,姿态解算方法主要有:四元数法、旋转矢量法、欧拉角法、方向余弦法和罗德利格参数法。1971年Bortz[1]提出的旋转矢量微分方程,为补偿载体在高动态环境下的圆锥误差提供了理论基础。基于此,国内外学者对基于旋转矢量的圆锥补偿算法进行了大量的研究,可概括为以下几个方面:增加子样数或前次周期项信息的圆锥算法系数设计[2-5]、通过补偿截断误差提高精度[6-7]、对周期项进行补偿[8]和圆锥算法结构设计[9]。但这些圆锥补偿算法都是以角增量作为输入,而目前广泛使用的光纤陀螺、微机械陀螺等输出为角速度,传统的圆锥补偿算法无法直接使用。

对于角速率输入,通常采用分段线性化,认为每一个时间段ΔT内的角速度为常量,由Δθ=ω·ΔT来计算角增量,不能有效地提高姿态角度精度[10]。黄昊、杜烨等[11-12]利用梯形公式、辛普森公式或其他数值积分方式得到角增量,代入到传统圆锥补偿算法会使补偿精度下降。针对以上问题,曾庆化等[13]推导出一类具有纯角速率输入的圆锥算法;Ben等[14]将Miller的思想引入圆锥算法设计,提出一种以角速率作为算法输入的改进锥面算法的广义方法;刘佳乐[15]直接利用角速率推导了双子样算法和加入前次周期信息的改进算法,测量精度得到了提高;汤传业等[16]在计算优化系数时采用最小二乘法,进一步提高了算法精度;卢世昕等[17]在前一周期的基础上对周期项进行了二次优化;丁鹏等[18]对单轴旋转捷联惯导系统,分析了基于角速率的多子样旋转矢量算法;Ding等[19]针对圆锥误差中的高阶补偿项,在计算等效旋转矢量时补偿了圆锥修正项和三交叉乘积项;邢丽等[20]建立了推力速度坐标系并引入等效螺旋矢量,并采用梯形数字积分方法计算等效螺旋矢量,对圆锥和划船误差同时进行了补偿。

目前,圆锥算法结构设计的研究分为双速结构、单速结构两类[20]。在分析角速率输入的双子样单速算法基础上,文中引入双速回路,研究了双子样的二次迭代算法,在推导优化系数时进行简化,减少了计算量。在经典圆锥运动环境下,对算法的可行性和有效性进行了仿真验证,仿真结果表明,该算法对提高捷联惯导系统的圆锥误差计算精度具有积极作用。

1 经典圆锥运动

基于圆锥误差可以由旋转矢量的微分方程表示,工程中经常通过分析旋转矢量的微分方程来设计算法。等效旋转矢量Φ表征载体系从tk-1至tk时刻的等效旋转,其微分方程可近似表示为[1]:

(1)

式中:ω为tk-1至tk时间段内的机体角速率;Φ为载体系由tk-1至tk时刻角位置变化所对应的等效旋转矢量。

假设t时刻载体仅存在锥运动,旋转矢量为[21]:

(2)

式中:α为锥运动的半锥角;Ω为锥运动的频率。

对应的锥运动四元数Q(t)为:

(3)

设从t至(t+h)时刻载体系的更新四元数为q(h),旋转四元数关系为[21]:

Q(t+h)=Q(t)⊗q(h)

(4)

即有

(5)

式中:h为姿态更新周期,其值为tk-1-tk。

(6)

2 基于角速率的二次迭代优化算法

2.1 双子样二次迭代算法推导

相比一次迭代的圆锥补偿算法,二次迭代算法是将姿态更新周期分为两个迭代周期,每个迭代周期内有N个角增量拟合采样点。对于角速率的双子样二次迭代算法,设姿态更新周期为h,迭代周期为T,采样周期为t,则有以下关系:

h=2T=4t

(7)

第一个迭代周期T1为[tk-1,tk-1+T],第二个迭代周期T2为[tk-1+T,tk-1+2T]。

在迭代周期T1内,假设载体系的角速率用二次曲线表示为:

ω(tk-1+τ)=a1+2b1τ+3c1τ2

(8)

式中:a1,b1,c1为多项式系数;0≤τ≤T。

将T1内的等效旋转矢量Φ(tk-1+T)作泰勒级数展开:

(9)

(10)

反解出的多项式系数可表示为:

(11)

将式(8)对τ求各阶导数:

(12)

其中i≥3。联立式(1)和式(12)可得:

(13)

其中i≥6。代入式(9)得:

(14)

将式(11)代入式(14)可得到T1内的旋转矢量:

(15)

在迭代周期T2内,假设载体系的角速率用抛物线表示为:

ω(tk-1+T+τ)=a2+2b2τ+3c2τ2

(16)

式中:a2,b2,c2为多项式系数;0≤τ≤T。

对应的旋转矢量用泰勒级数展开:

(17)

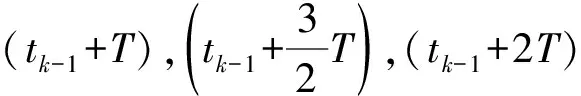
(18)

2.2 系数优化

上面推导出的角速率交叉项系数是以抛物线拟合角速度得出的,但实际角速度不一定如此,因此需对这些系数进行修正以保证拟合所得的算法漂移最小。

当系统绕x轴作圆锥运动时,设

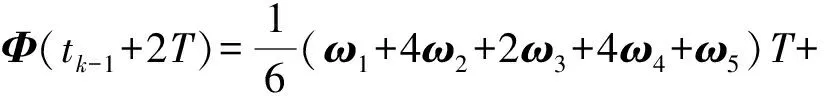
(19)

式中:k1,k2,k3,k4为待定优化系数,使得在圆锥运动环境下的算法漂移最小。考虑到计算量和工程化,圆锥误差项仅计算3个叉乘项足以保证算法的精度,过多反而增加计算负担且精度提升不明显,因此将式(19)简化为:

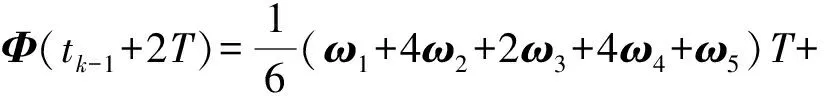
(20)

仅考虑x轴直流分量,将式(6)代入式(20),得

(21)

根据精度准则[2],有:

(22)

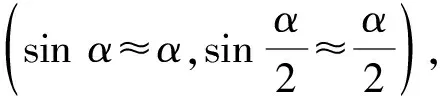
(23)

由于Ωh远小于1,令(ΩT)3、(ΩT)5和(ΩT)7项系数为零,解得:

(24)

综上所述,基于角速率的双子样二次迭代算法可表示为:

(25)

算法漂移为:

(26)

3 仿真实验与分析

把典型圆锥运动直接作为测试输入环境,将传统双子样算法(Method 1)[21]、传统双子样二次迭代算法(Method 2)[22]、基于角速率的双子样优化算法(Method 3)[15]、基于角速率的三子样优化算法(Method 4)[15]、与文中算法(Method 5)进行比较,验证文中提出的姿态算法的性能。

设置3组仿真条件:1)半锥角α为1°,圆锥运动频率f为1 Hz,姿态更新周期h为24 ms,仿真总时长为10 s。2)半锥角α为1°,圆锥运动频率f为10 Hz,姿态更新周期h为2.4 ms,仿真总时长为10 s。姿态角解算误差如图1～图2所示;仿真时间内Method 1～Method 5在两种圆锥运动环境下的最大姿态角误差分别如表1～表2所示。3)半锥角α为1°,陀螺采样间隔为2 ms,改变圆锥运动频率,对Method 2和 Method 5两种算法在x轴上的俯仰角误差的最大值进行仿真,结果如表3所示。

图1 各算法在条件1下的姿态角误差Fig.1 Attitude angle error of each algorithm under condition 1

图2 各算法在条件2下的姿态角误差Fig.2 Attitude angle error of each algorithm under condition 2

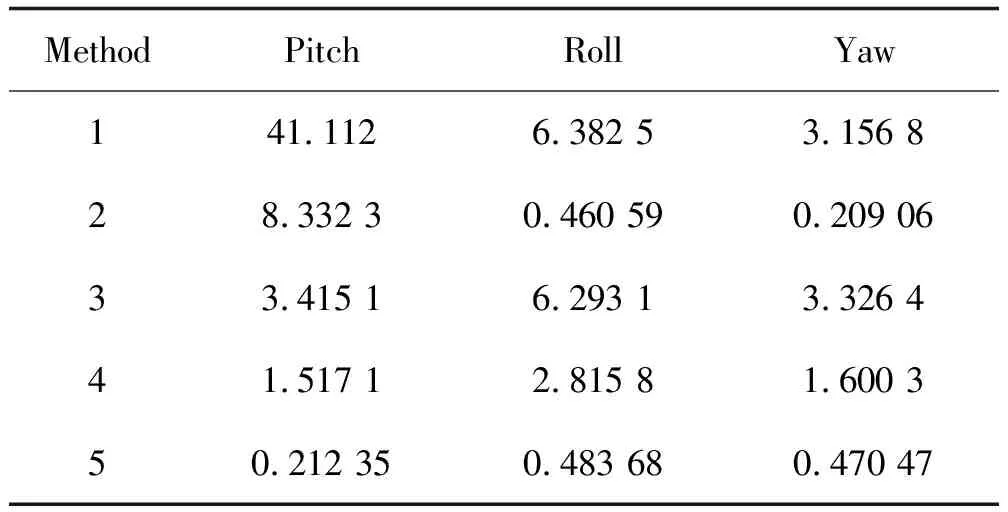
表1 条件1下各算法姿态角误差最大值

表2 条件2下各算法姿态角误差最大值

对比条件1和条件2可知,在不考虑陀螺采样上限的情况下,随着圆锥运动频率的增大,姿态更新周期相应减小,算法的精度相差仅一个数量级,验证了算法的可行性和有效性,说明文中算法能在高动态环境下保证算法性能。

对比Method 1和Method 3,Method 2和Method 5可看出,在相同仿真条件下,当陀螺输出为角速率时,采用梯形公式或辛普森公式等提取角增量再代入传统的旋转矢量算法,不仅在精度上存在局限,而且求出的角增量之和存在误差,基于角速率的圆锥补偿算法能够明显提高计算精度。对比Method 4和Method 5可看出,相比基于角速率的双子样和三子样的一次迭代算法,文中提出的改进算法精度更高,且叉乘运算量和三子样优化算法相同,使姿态精度和稳定性得到了进一步的改善。

为了更加清晰和明确地说明文中算法与传统算法相比较的优势,表3统计了Method 2和Method 5两种算法在相同圆锥条件下,姿态解算误差的最大值对比结果。

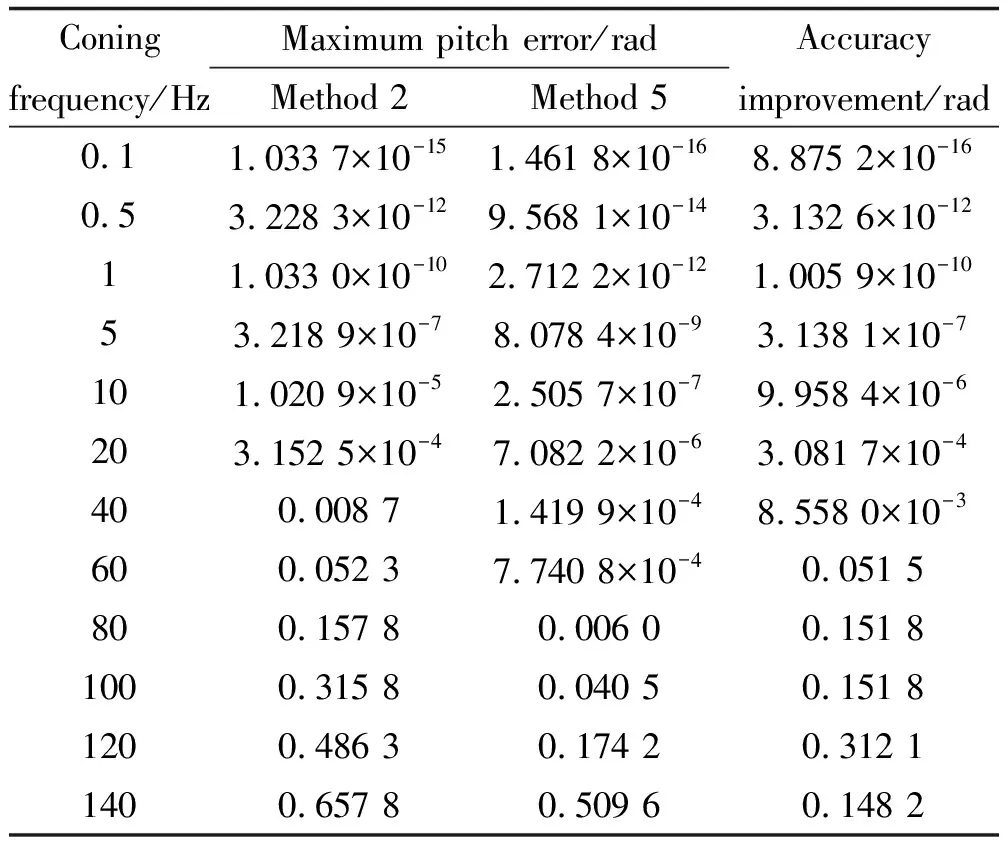
表3 2 ms采样间隔下x轴上俯仰角误差最大值

从表3中可以看出,随着圆锥运动频率的增大,导航解算误差的最大值均小于传统算法1～2个数量级,即载体的运动幅值变大时,文中算法的姿态解算精度更优于传统算法。

4 结论

为解决传统姿态算法在角速率输入时计算精度较低、不能有效补偿圆锥误差的问题,文中在双子样一次迭代的基础上,提出了采用双子样二次迭代的旋转矢量姿态算法,推导了能够满足工程运用的算法简化表达式。仿真结果表明,提出的姿态算法与传统算法、基于角速率的双子样和三子样的一次迭代算法相比,具有更高的姿态解算精度,且叉乘运算量和三子样优化算法相同。故提出的角速率输入下二次迭代的双子样旋转矢量姿态算法具有一定的应用价值。