基于雷达组合多模型联合火箭弹径向速度预测

田 珂，雷 红，常华俊，冷雪冰，段鹏伟

(63861部队，吉林白城 137001)

0 引言

常规兵器试验中,通常利用弹道测量雷达测试火箭弹主动段的飞行坐标,同时利用连续波雷达测试火箭弹主动段的径向速度。正常情况下,两台雷达能够全程测试火箭弹全弹道飞行坐标和径向速度。但是有时连续波雷达参试中途会因为设备老化出现死机、人为操作失误等突发故障,此时雷达就会出现测试异常,导致错过对某段时间径向速度的准确捕捉。此外,火箭弹在高空飞行过程中由于自身原因或者遇上大风等不良天气时,飞行轨迹就会短暂偏离雷达波束辐射范围,就会缺失该段的数据;当理论弹道本身存在偏差时,雷达一开始就会按照错误的弹道轨迹进行布站和调参,同样会导致无法全程准确捕捉目标。上述问题最后都会导致连续波雷达无法准确测试出火箭弹某时间段的径向速度,数据的缺失会在一定程度上影响对火箭弹相关指标的准确测试和毁伤效能的准确评估。针对这些问题,建立合理的模型预测出缺失的径向速度并对数据进行重构就非常必要。目前有很多研究弹丸径向速度的文献[1-3]:文献[1]主要研究如何对弹丸径向速度进行实时高精度处理,前提是雷达能够完整捕获到弹丸的径向速度,并未考虑弹丸径向速度缺失时的解决办法;文献[2]提出了在弹丸径向速度缺失时,利用回归模型预测出缺失的数据,但其主要研究的是大口径弹丸,并未提到小口径弹丸的解决办法,也没有考虑单项模型预测精度不理想的情况;文献[3]研究的是根据径向速度检测低速目标的问题,前提依然是获取到部分径向速度,当径向速度不完整时该方法无法应用。以上文献都是研究的普通炮弹,普通炮弹出炮口后在惯性作用下进行运动,而火箭弹在出炮口后是在火箭推力的作用下进行运动,所以文献[1-3]所提方法对火箭弹不一定适用。由于火箭弹在主动段受到多种作用力的影响,其径向速度存在微小波动,这些波动特征既包含线性变化,也包含一定的非线性变化,所以单纯利用传统单一模型进行预测,预测精度往往很难得到保证。虽然传统时间序列模型可以根据数据的变化趋势进行后期预测,但是只能按照时间先后顺序进行预测,当遇到多段径向速度出现缺失且缺失前的样本数据量又很少时,预测精度将大打折扣,所以传统方法存在一定应用限制。

为解决以上不足,进行两点创新:一是选择把两台雷达的数据进行深度融合,即使样本数据量不够多,也可以建立适合的模型提高预测精度,而且也不用再考虑射击弹丸口径大小的问题,因为不论火箭弹是大口径还是小口径,主动段都会受到发动机的推力作用,径向速度变化规律基本一致,两台雷达进行数据融合的方法是通用的,而且针对所建样本融合数据,也可以引入更多的模型进行预测,不再受限于时间序列模型,为建立组合模型奠定基础。此外,文献[2]研究的是大口径弹丸,大小口径弹丸出炮口后的运动规律会有一定区别,但是同样可以将弹道测量雷达的坐标与连续波雷达的径向速度进行融合,根据径向速度的变化规律建立适合的模型进行预测,所建模型可能略有区别,但方法和思路是通用的,解除了只能建立单一模型进行预测的限制,拓宽了预测方法,提高了预测精度。两台雷达数据融合的具体原理是:弹道测量雷达与连续波雷达测试的是同一发火箭弹,前者测试飞行坐标,后者测试径向速度,坐标中的射程x与横偏z基本上都是线性变化,与径向速度有共同的变化特征,同时径向速度又存在一定的非线性特征,所以选择把弹道坐标作为特征向量,径向速度作为目标向量,分别建立径向速度与射程的一元线性回归模型、径向速度与横偏的一元线性回归模型、径向速度与射程和横偏的支持向量回归机模型,线性回归模型负责挖掘出线性成分,支持向量回归机负责挖掘出非线性成分。神经网络具有非常强的复杂非线性系统建模能力,但是需要大量的样本数据才能训练充分[4],所以选择利用支持向量回归机挖掘出非线性成分[5]。此外,支持向量回归机的预测精度容易受到核函数参数的影响,所以使用遗传算法对核函数参数进行寻优搜索,最后再建立遗传算法优化(least square support vector machine,LSSVM)模型。

二是得到4个模型预测值后再根据组合模型建模原理计算出组合模型预测值,具体原理是:计算出每个模型每期预测值与实测值的误差平方,然后建立预测值与误差平方的一元线性回归模型,再把剩余部分预测值带入到所建回归模型中,就可以预测出对应的误差平方,最后再利用预测出的误差平方,计算出每个模型每期预测值对应的权系数,每期预测值乘以对应的权系数再相加,就得到了多模型联合预测值。实验结果表明,多模型联合预测值与对应实测值的平均绝对百分比误差为0.065%,小于1‰,也小于GM(1,1)(grey model,GM)灰色模型等对比模型的预测误差,达到了连续波雷达测试火箭弹径向速度的误差要求,所采用的方法可以用来预测火箭弹的径向速度。

1 一元线性回归模型原理

一元线性回归模型是描述两个变量之间相互关系(线性关系)的模型,该模型假设因变量y只受到一个自变量x的影响,它们之间存在类似线性函数的关系,用一元线性回归方程可表示为[6]:

y=αx+b+ε

(1)

式中α和b是回归系数。

一元线性回归方程的目的是找出一条直线,使所有的样本数据尽可能的落在它的附近。对一元线性回归方程预测结果进行检验:1)检验方程的显著性。根据F检验法对应的概率p值与临界统计值的比较结果进行判定,如果概率p值远小于临界统计值0.05,说明回归模型是显著的,即所建立的一元线性回归模型成立,否则回归模型不显著,即模型不成立;2)检验模型的拟合效果。如果检验结果显示multiple R-squared和adjusted R-squared两个参数均非常接近1,说明模型的拟合效果很好,否则说明模型拟合效果并不好,需要重新调整模型;3)检验回归系数的显著性。如果回归系数对应的概率p值远小于临界统计值0.001,说明回归系数是显著的,否则不显著,需要重新调整模型。

2 支持向量回归机原理

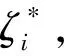
(2)

(3)

3 遗传算法优化LSSVM原理

针对线性问题,最小二乘支持向量机的优化目标为求解公式(4)的最小值。

(4)

引入拉格朗日函数并对相关参数求导,得到最小二乘支持向量机的回归函数与公式(2)和(3)基本一致。核函数参数和正则化参数是影响最小二乘支持向量机性能的敏感参数,通过合理的选择,可以提升最小二乘支持向量机的泛化能力。而遗传算法可以很好的对这两个参数进行优化。遗传算法(genetic algorithm,GA)是一种模拟自然界生物进化过程来搜索最优解的方法,按照确定的适应度函数,采用遗传算子对种群中的个体进行操作,通过在个体间不断交换染色体信息使种群得以进化,最终使适应值好的个体得以保留,把适应值差的个体淘汰掉。遗传算法优化核函数参数和正则化参数的过程:先设定核函数参数和正则化参数的寻优范围,同时设定遗传算法适应度函数、基因变异的概率、种群规模、进化代数等参数,然后输入训练数据和测试数据,用遗传算法对两个参数进行寻优操作,检验是否达到迭代次数,如果达到了设定的迭代次数,利用搜寻出的最优参数建立最优的LSSVM模型,否则重新调整模型。利用遗传算法搜索LSSVM核函数参数与正则化参数的步骤如图1所示。

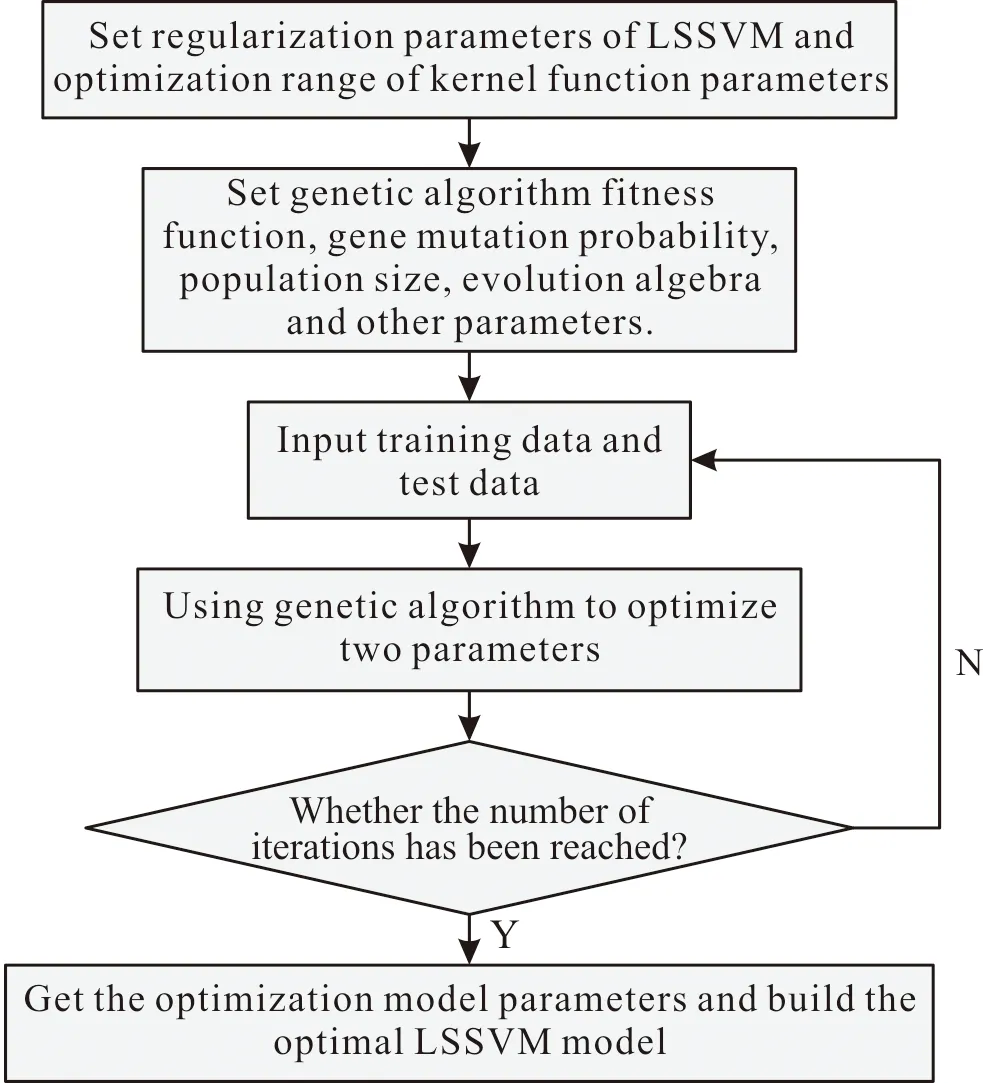
图1 遗传算法优化LSSVM参数的过程Fig.1 Process of optimizing LSSVM parameters by genetic algorithm

4 雷达组合与多模型联合原理

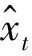
(5)

(6)

(7)

(8)

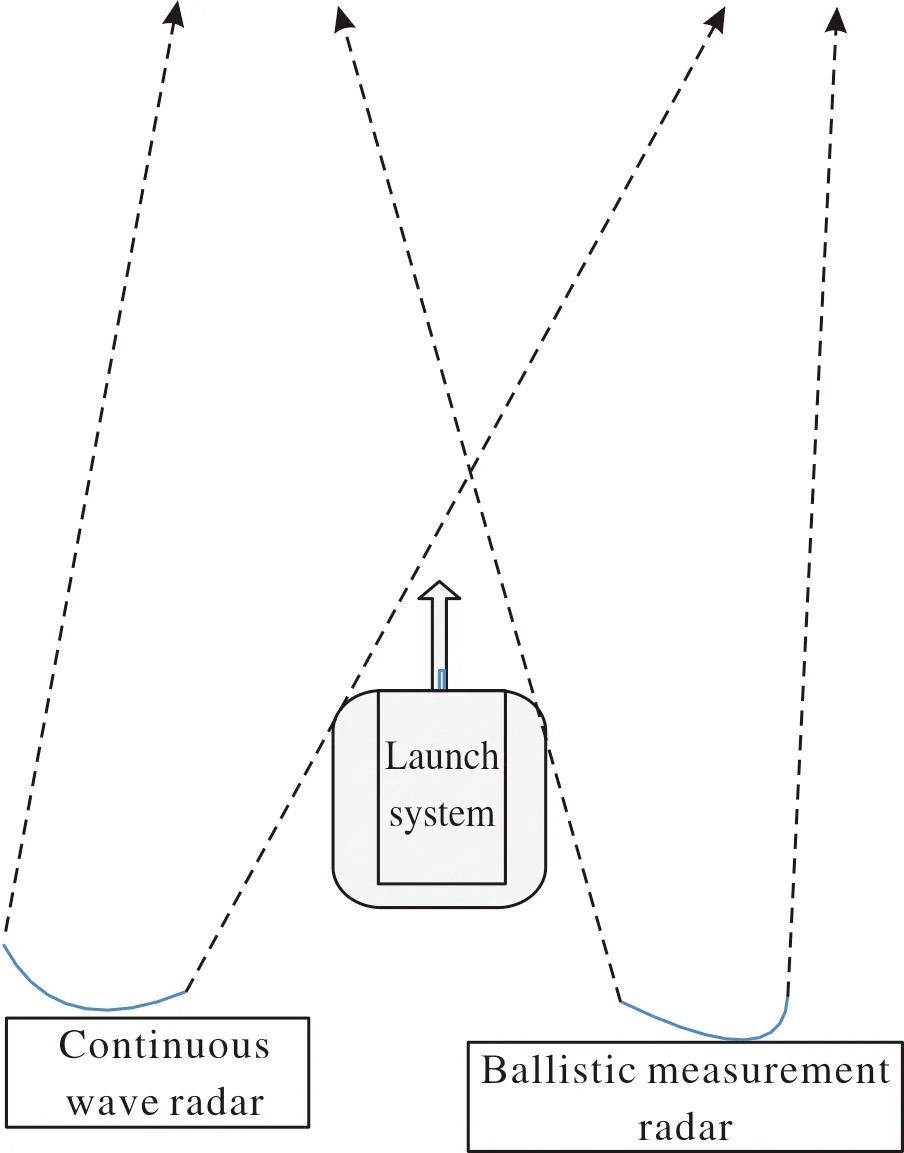
图2 雷达现场布站示意图Fig.2 Schematic diagram of radar site layout

5 实验验证

选择利用RStudio软件环境进行数据分析、统计建模及数据可视化。雷达测试火箭弹径向速度较为完整的瀑布图如图3所示,径向速度存在缺失的瀑布图如图4所示。由于在工程实践中,出现过在10.1～12.0 s雷达跟丢弹丸的情况,所以选择利用弹道测量雷达和连续波雷达共同测试的火箭弹飞行坐标和径向速度实测值进行建模预测,具体如图5所示,径向速度按照统一标准对原始数据进行了数量级处理。由于射程、横偏与径向速度的取值范围偏差较大,为了提高模型收敛速度,避免取值对模型精度的影响,采用式(9)对所有数据进行了归一化处理[10]。

(9)

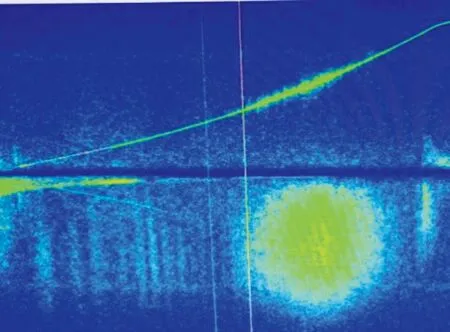
图3 径向速度完整的瀑布图Fig.3 Complete waterfall diagram of radial velocity

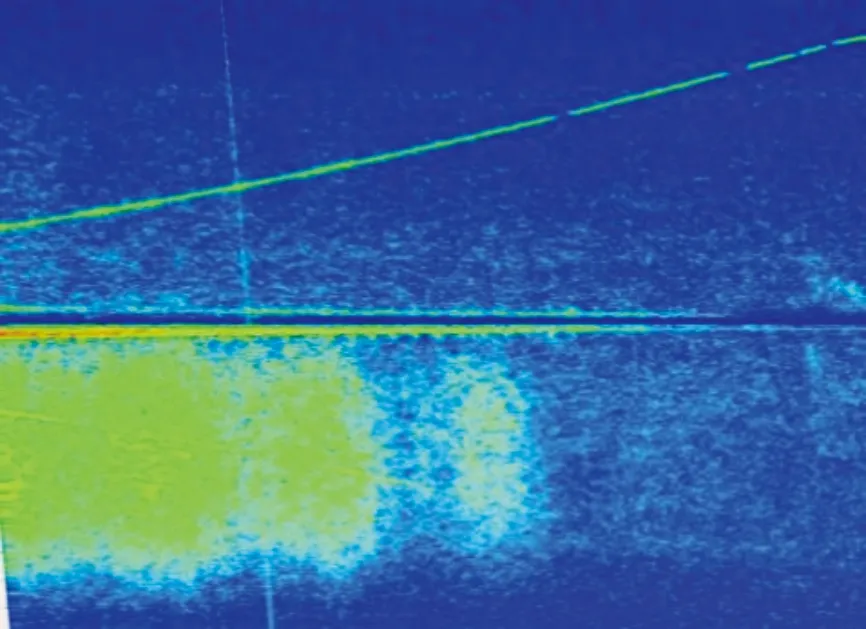
图4 径向速度存在残缺的瀑布图Fig.4 Incomplete waterfall diagram of radial velocity

图5(a)、图5(b)分别是弹道测量雷达测试的火箭弹飞行坐标中射程、横偏与时间的关系曲线,每个数据点的时间间隔是0.1 s,共有120个数据点;图5(c)是连续波雷达测试的火箭弹径向速度与时间的关系曲线,每个速度点的时间间隔是0.1 s,共有120个速度点;图5(d)和图5(e)分别是径向速度与射程、横偏之间的关系曲线;图5(f)是径向速度与射程和横偏的三维关系曲线。可以看出连续波雷达测试的径向速度与弹道测量雷达测试的射程、横偏基本上呈线性关系,初步判断适合建立一元线性回归模型。

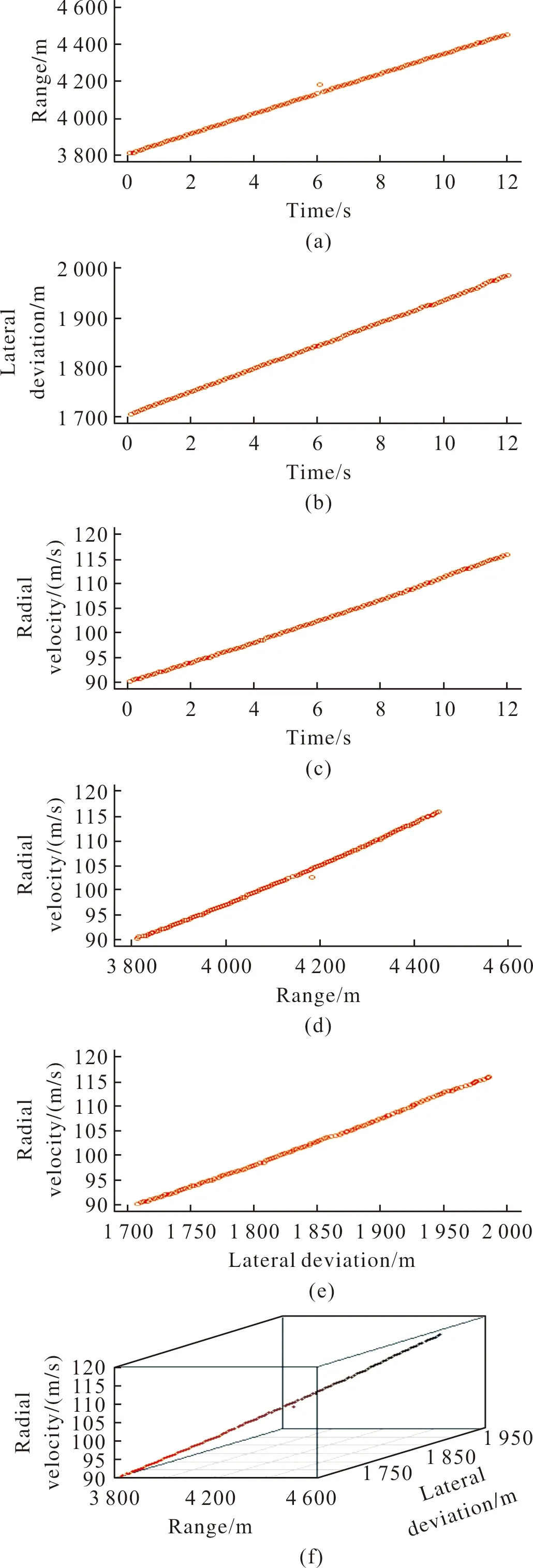
图5 弹道测量雷达和连续波雷达测试的坐标和径向速度关系图Fig.5 Relationship between coordinates and radial velocity of ballistic measurement radar and continuous wave radar

首先进行数据探索,发现射程中第61个数据点属于离群点,删除该离群点,同时建立射程与时间的一元线性回归模型,预测出射程第61个数据点进行插值,插入值为4 139.245,然后绘制径向速度与射程和横偏的3维立体关系曲线如图6所示,可以看出删除离群点并插入预测值后径向速度与射程和横偏依然呈线性关系。

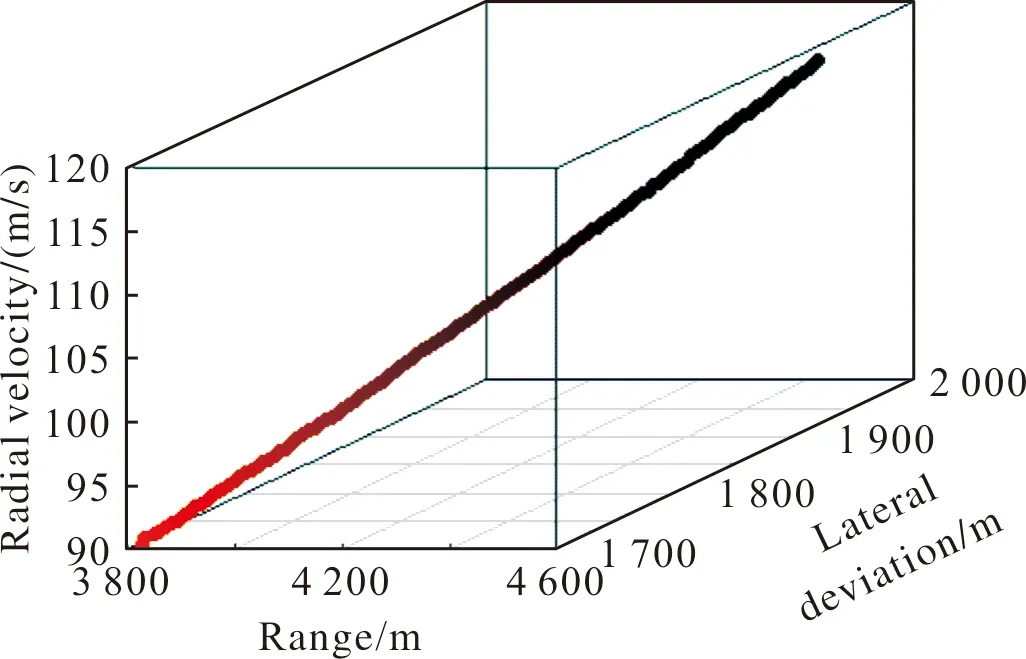
图6 删除离群点后径向速度与射程、横偏的三维关系曲线Fig.6 Three dimensional relationship curve of radial velocity with range and lateral deviation after deleting outliers

建模前需要考量数据的相关关系,检验自变量与因变量关系的方向和强弱。计算自变量射程与因变量径向速度之间的相关系数并绘制相关系数矩阵,如图7所示,圆形区域的颜色越靠近蓝色且越深,说明相关系数越接近1,两个特征变量的正相关性越强,颜色越接近红色且越深,说明两个变量的相关系数越接近-1,负相关性越强,颜色越接近白色,说明两个特征变量之间没有相关性。可以看出射程与径向速度之间是正向强相关的关系,说明自变量射程有利于提升预测因变量径向速度的精度。计算自变量横偏与因变量径向速度之间的相关系数并绘制相关系数矩阵,如图8所示,可以看出横偏与径向速度也是正向强相关的关系,更加确定所建立的径向速度与射程一元线性回归模型、径向速度与横偏一元线性回归模型是合理的,与图5所表达的特征基本一致。

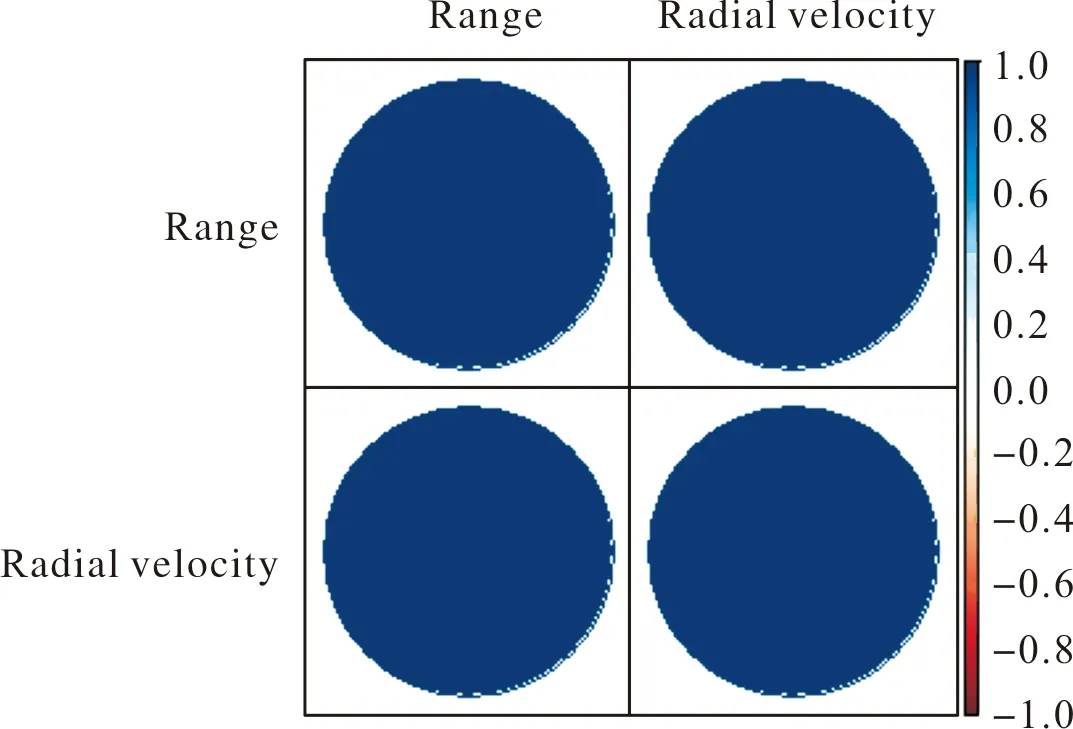
图7 射程与径向速度之间的相关系数矩阵Fig.7 Correlation coefficient matrix between range and radial velocity

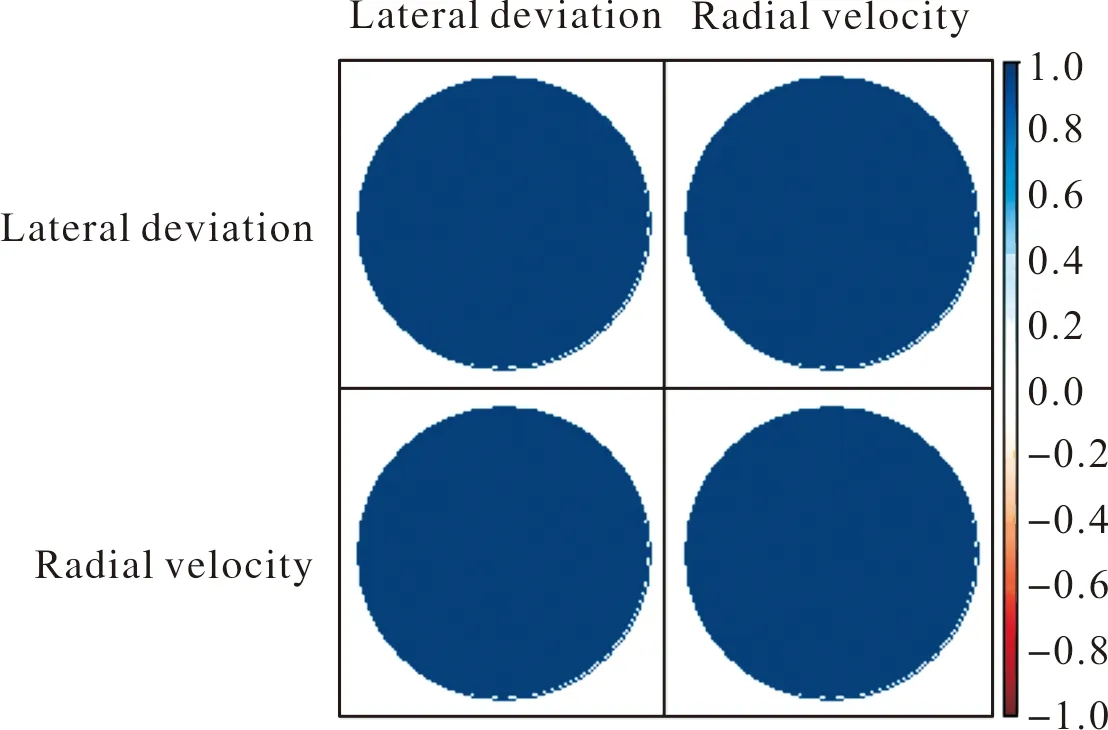
图8 横偏与径向速度之间的相关系数矩阵Fig.8 Correlation coefficient matrix between transverse deflection and radial velocity

由于在10.1～12.0 s之间雷达测试火箭弹径向速度出现缺失的情况,所以选择把0.1～10.0 s之间共100个数据作为训练数据,10.1～12.0 s之间共20个数据作为测试数据。在此之前,先把0.1～5.0 s之间共50个数据作为训练数据,分别建立径向速度与射程和横偏的一元线性回归模型,以及径向速度与射程和横偏的支持向量回归机模型,然后再把5.1～10.0 s之间的射程和横偏分别带入到建立的3个模型中,就得到了3个模型预测出的5.1～10.0 s之间的径向速度,然后把这3个模型预测值作为特征向量,对应的5.1～10.0 s之间径向速度实测值作为目标向量,建立遗传算法优化LSSVM模型。随后,利用0.1～10.0 s之间的射程、横偏、径向速度分别建立径向速度与射程一元线性回归模型、径向速度与横偏一元线性回归模型,以及径向速度与射程和横偏的支持向量回归机模型,再把10.1～12.0 s之间的射程、横偏带入到建立的3个模型中,就得到了3个模型预测出的10.1～12.0 s之间的径向速度,最后把这3个预测值带入到建立好的遗传算法优化LSSVM模型中,就得到了遗传算法优化LSSVM预测出的10.1～12.0 s之间的径向速度。在建立径向速度与射程的一元线性回归模型中,模型检验结果显示,回归方程的显著性检验结果对应的概率p值为2.2×10-16,远小于临界统计值0.05,说明所建回归模型是显著的,参数Multiple R-squared为0.998 6,参数Adjusted R-squared为0.998 6,均非常接近1,说明所建回归模型的拟合效果非常好,回归系数对应的概率p值为2×10-16,远小于0.001,说明回归系数是显著的,表明所建速度-射程回归模型通过了检验;建立径向速度与横偏的一元线性回归模型时,模型检验结果显示,回归方程的显著性检验结果对应的概率p值为2.2×10-16,远小于临界统计值0.05,说明所建回归方程是显著的,参数Multiple R-squared为0.999 8,参数Adjusted R-squared为0.999 8,均非常接近1,说明所建回归方程拟合效果非常好,回归系数显著性检验结果对应的概率p值为2×10-16,远小于临界统计值0.001,说明回归系数是显著的,总体可知所建径向速度-横偏的一元线性回归方程通过了检验。利用支持向量回归机解决非线性问题时,最关键的部分是引入核函数将样本数据映射到高维空间使其转化为高维空间中的线性回归问题,常用的核函数有线性核函数、径向基核函数、多项式核函数和sigmoid核函数。不同核函数下,支持向量回归机预测出的第5.1～10.0 s之间的数据与实测值关系曲线如图9所示。

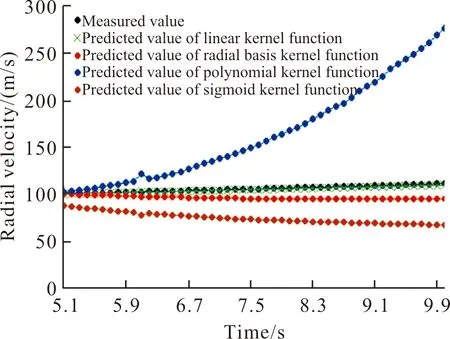
图9 不同核函数支持向量回归机预测值与实测值关系曲线Fig.9 Relationship curve between predicted value and measured value of support vector regression machine with different kernel functions

从图9可以看出,利用线性核函数建立的支持向量回归机预测值与实测值最接近。实际上由于径向速度与射程、横偏主要是线性关系,所以支持向量机的核函数选择线性核函数也是合理的。建立好3个模型后,再把5.1～10.0 s测试数据对应的射程和横偏分别代入到所建立的3个预测模型中,就可以得到5.1～10.0 s之间径向速度射程回归预测值、横偏回归预测值和支持向量回归机预测值。采用同样的方法,再把0.1～10.0 s之间的数据点作为训练数据,10.1～12.0 s之间的数据点作为测试数据,就能得到10.1～12.0 s之间的径向速度对应的射程回归预测值、横偏回归预测值和支持向量回归机预测值,绘制5.1～12.0 s之间径向速度实测值与3个模型预测值的关系曲线如图10所示。

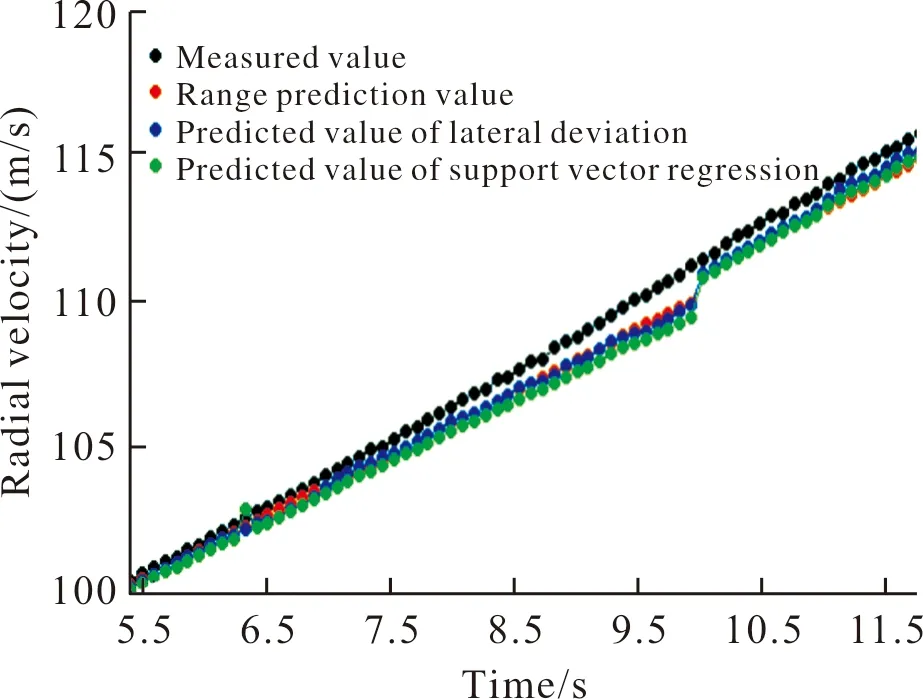
图10 径向速度5.1～12.0 s实测值与所有模型预测值关系曲线Fig.10 Relationship curve between measured values of radial velocity from 5.1 s to 12.0 s and predicted values of all models

针对图10,选择把5.1～10.0 s之间共50个数据作为训练数据,10.1～12.0 s之间共20个数据作为测试数据。先把径向速度5.1～10.0 s之间射程回归预测值、横偏回归预测值和支持向量回归机预测值作为特征向量,径向速度5.1～10.0 s之间的实测值作为目标向量,建立遗传算法优化LSSVM模型,遗传算法选择把核函数的参数和正则化参数的寻优范围设置为0到300,种群规模设置为100,最大迭代次数设置为100,基因突变的概率设置为0.01,把均方根误差作为适应度函数,最后经过100次迭代,搜寻出的最佳核函数参数和正则化参数分别为299.288 4和299.447 1,均方根误差随迭代次数的变化曲线如图11所示,横坐标表示迭代次数,纵坐标表示误差。

然后再把10.1～12.0 s之间径向速度射程回归预测值、横偏回归预测值以及支持向量回归机预测值代入到建立好的遗传算法优化LSSVM模型中,就可以得到遗传算法优化LSSVM模型预测出的10.1～12.0 s之间的径向速度。10.1～12.0 s径向速度实测值与所有模型预测值如表1所示。由于组合模型的权系数是根据预测值与实测值计算出来的,但是在实际问题中并不知道实测值,需要将其预测出来,所以先要计算出权系数。为此,先根据10.1～11.0 s之间所有模型每期预测值与实测值计算出误差平方,接着建立误差平方与预测值的一元线性回归模型,再把11.1～12.0 s之间的4个模型预测值带入到所建一元线性回归模型中,就得到了11.1～12.0 s 4个模型预测值对应的误差平方,如表2所示,然后再根据误差平方并结合式(8)～式(10)就可以计算出11.1～12.0 s所有预测模型每期预测值对应的权系数,再乘以对应的预测值,相加之后就得到了组合模型预测值,如表3所示。11.1～12.0 s之间实测值与所有模型预测值关系曲线如图12所示。

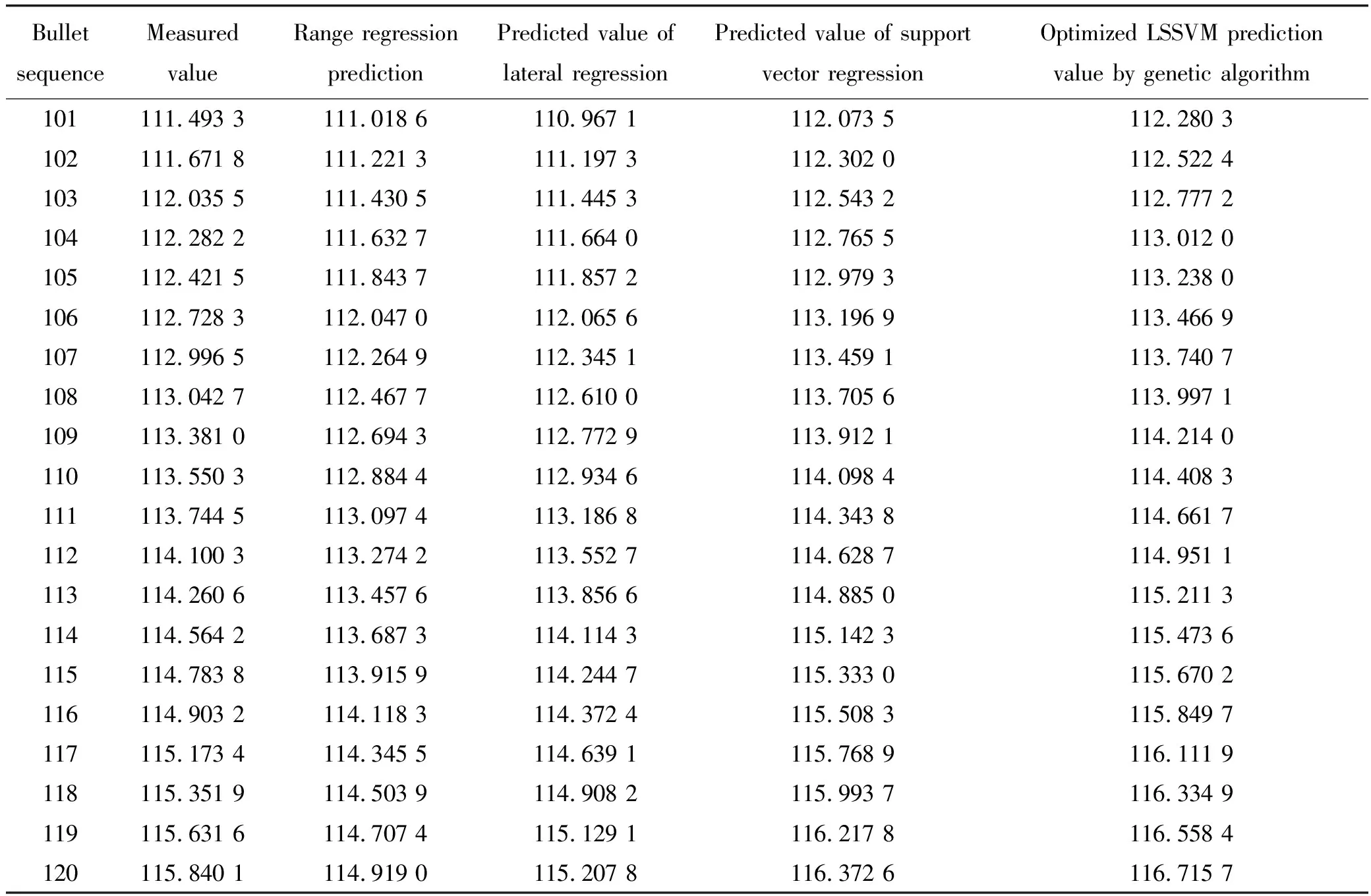
表1 10.1～12.0 s之间径向速度实测值与所有模型预测值Table 1 Measured radial velocity values and predicted values of all models between 10.1 s and 12.0 s m/s

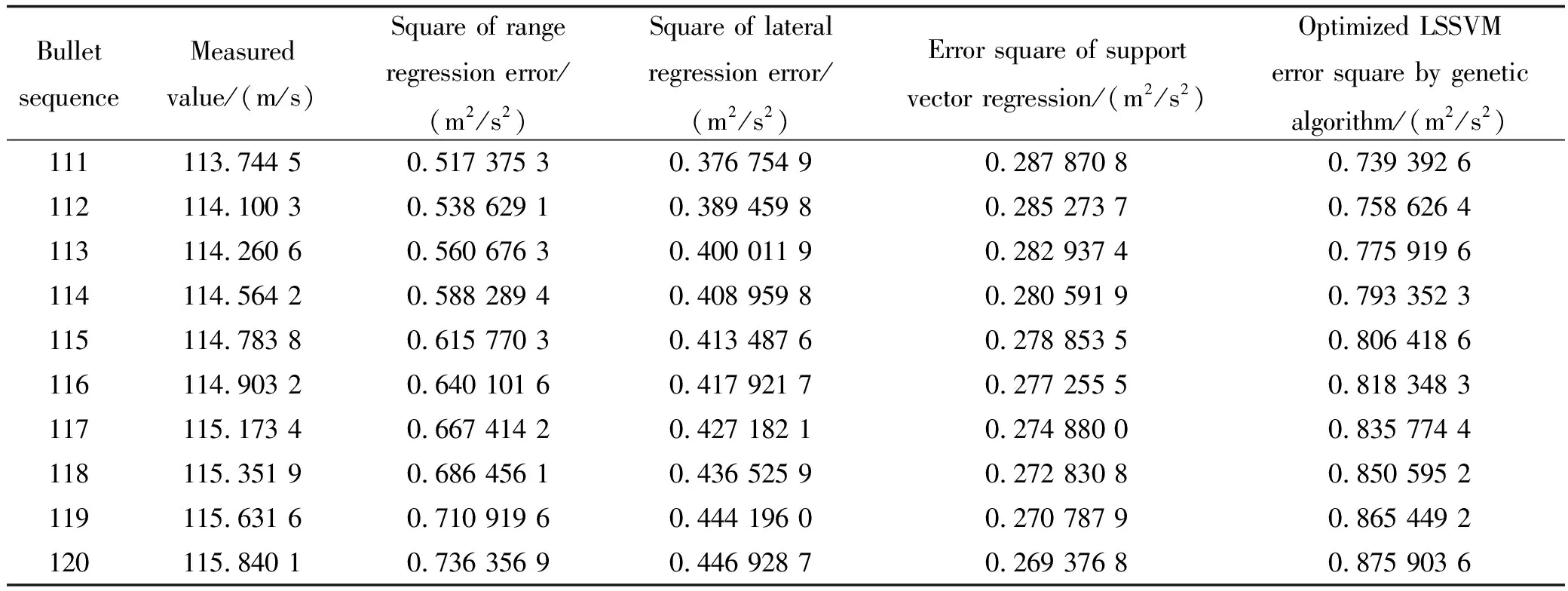
表2 11.1～12.0 s之间预测出的所有模型预测值对应的误差平方Table 2 Error squares corresponding to the predicted values of all models predicted between 11.1 s and 12.0 s

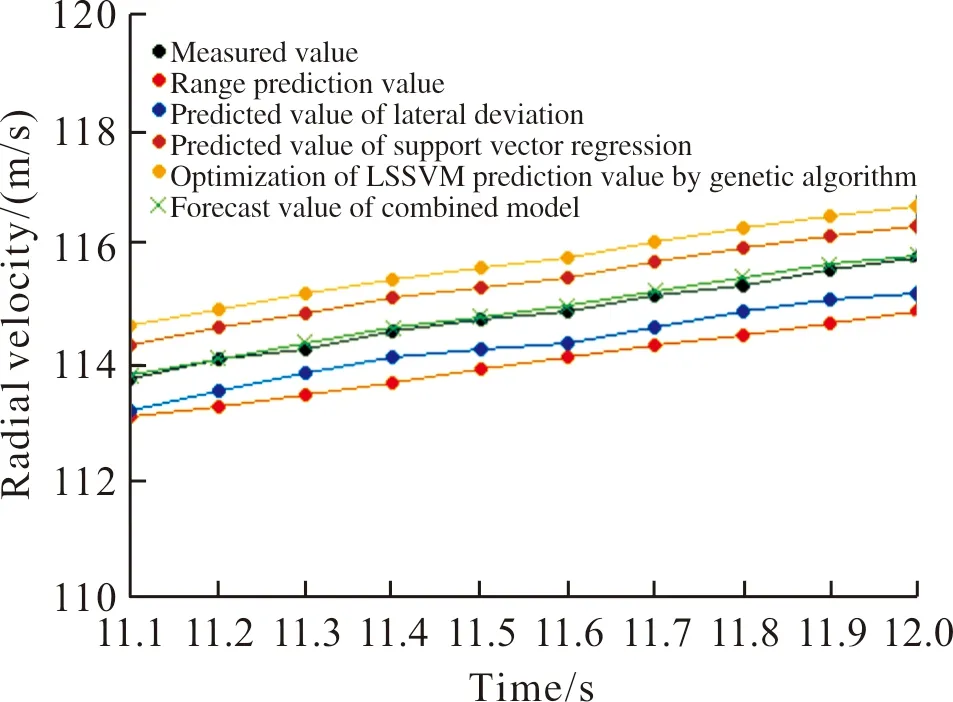
图12 径向速度11.1～12.0 s实测值与所有模型预测值关系曲线Fig.12 Relationship curve between measured values of radial velocity and predicted values of all models from 11.1 s to 12.0 s

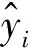
(10)

从图12可以看出,径向速度11.1～12.0 s之间组合模型预测值最接近实测值。根据表1计算得到,射程回归预测值与实测值的平均绝对百分比误差为0.725%,横偏回归预测值与实测值的平均绝对百分比误差为0.448%,支持向量回归机预测值与实测值的平均绝对百分比误差为0.509%,遗传算法优化LSSVM预测值与实测值的平均绝对百分比误差为0.799%,组合模型预测值与实测值的平均绝对百分比误差为0.065%,小于1‰,组合模型预测值与实测值的绝对误差与实测值乘以1‰的关系曲线如图13所示。

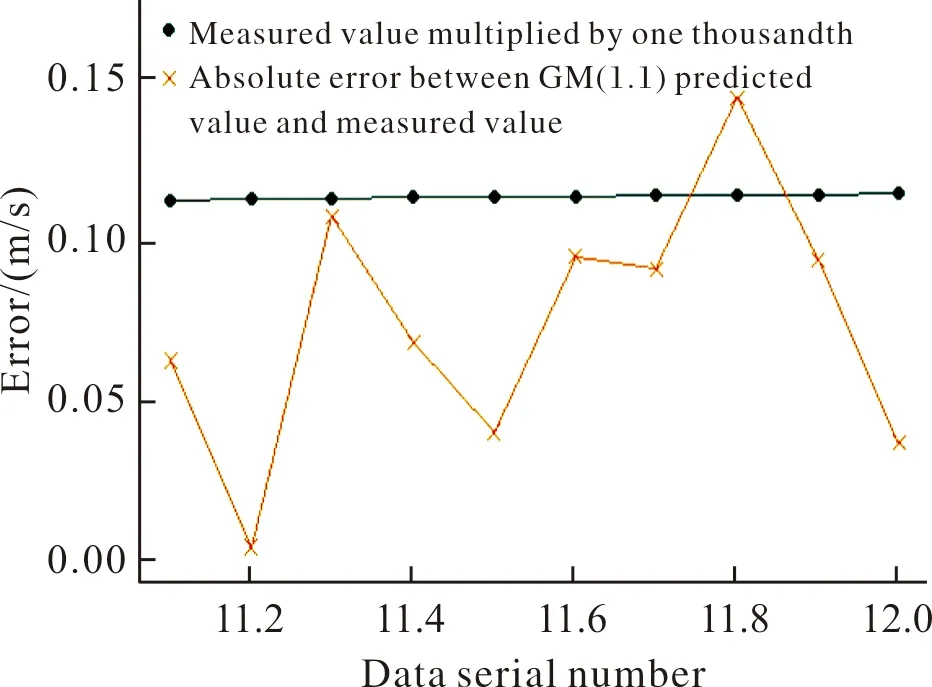
图13 绝对误差与实测值乘以1‰误差标准的关系曲线Fig.13 Relation curve between absolute error and measured value multiplied by 1‰ error standard

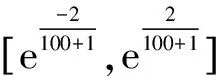
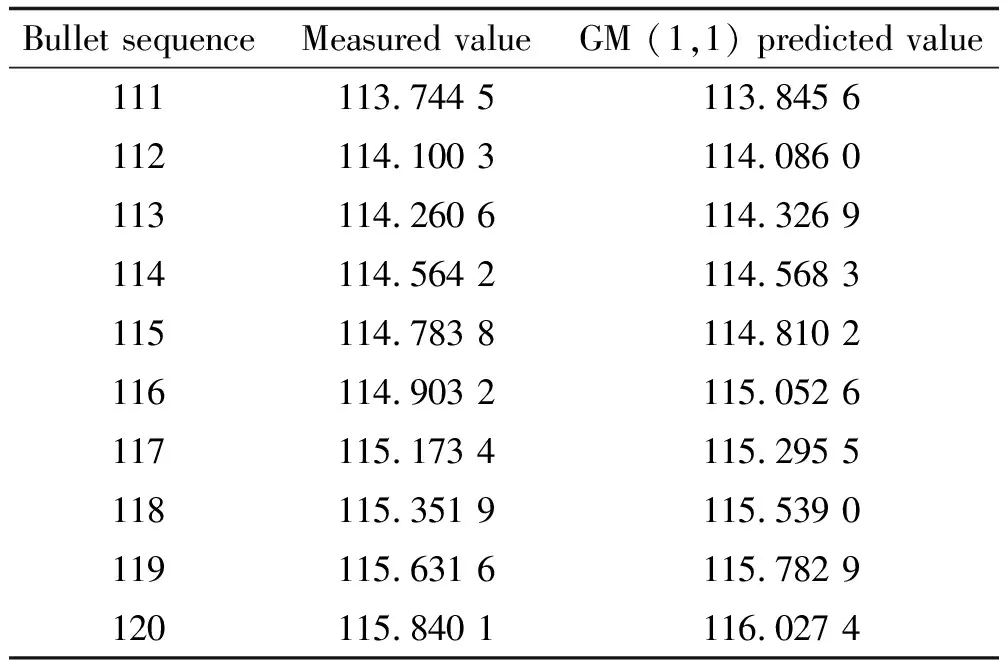
表4 实测值与GM (1,1)模型预测值Table 4 Measured values and GM (1,1) model predicted values m/s

总体而言,虽然GM(1,1)模型预测精度很高,整体的预测误差小于1‰,而且单项预测误差大多数也小于误差标准,但无法与组合模型相比,组合模型的预测精度更有优势,充分证明所采用方法在预测火箭弹主动段径向速度的优越性[11]。实际上,火箭弹在主动段的径向速度容易受到天气、风速等参试客体的影响,使得径向速度会出现随机变化,此时GM(1,1)模型的预测能力就会稍显不足,反而所采用的组合模型无论什么情况下都能够同时涵盖径向速度中的线性特征和非线性特征。当径向速度受到外界参试客体的影响时,只要保证具有大量的样本数据,组合模型就具有更强大的泛化能力,使得预测精度能够得到充分保证。

6 结论

针对火箭弹径向速度容易出现缺失的情况,选择把坐标作为特征向量,径向速度作为目标向量,进行建模预测,主要得出以下结论:

1)把弹道测量雷达的数据与连续波雷达的数据进行融合,把线性回归模型、支持向量回归机模型和遗传算法优化LSSVM模型进行联合组合使用,能够充分挖掘出径向速度中的线性特征和非线性特征。实验结果表明,相比所有模型,建立在组合方法上的多模型联合预测值,不论是整体的预测精度还是单项预测精度,都达到了连续波雷达测试火箭弹径向速度的精度要求。

2)所采用的方法有效解决了当径向速度大范围缺失,同时可用样本数据又很少,利用时序模型预测精度不高的问题,采用所提方法可以较为准确预测出缺失的径向速度,为较为准确预测火箭弹径向速度提出了新的研究方向。

3)靶场试验中还有很多其他试验科目比如利用连续波雷达测试着靶速度,利用初速雷达测试弹丸初速等也出现需要对数据进行重构的问题,利用所提方法可以为其他试验科目提供借鉴。此外,当样本数据足够多时可以考虑采用BP神经网络进行预测,因为神经网络在大量样本数据下才能训练充分,预测精度和泛化能力都比一般模型强很多。

4)文中选择利用预测值与误差平方建立一元线性回归模型,预测出剩余预测值对应的误差平方,这是因为径向速度存在明显的单调趋势,如果换成其他数据存在很强的非单调趋势,可以考虑建立多项式回归模型或者非线性映射模型进行预测。