火箭RCS仿真和修正方法研究

魏明山，刘光花，张 强

(酒泉卫星发射中心，甘肃 酒泉 732750)

0 引言

近年来,随着导弹和反导体系的不断发展,针对导弹目标RCS仿真的研究较多[1-6],目的是通过仿真获得导弹目标RCS特征,实现弹头目标的有效识别。导弹保密要求高,难以获得真实数据进行验证分析,与导弹类似的火箭目标具有飞行次数多、测量数据多和公开资料多的优点,因此先研究火箭仿真再推广到导弹目标是一条可行之路。导弹和火箭是典型的电大目标,电大目标RCS获取技术是当前的难点和热点。目前国内外目标RCS获取途径主要有三种,第一种是采用暗室测试的方法,由于电大目标尺寸大,对暗室要求高,像火箭这样的电大目标几乎不可能采用暗室测试方法实现;第二种是外场测试,受外场远场环境要求和测量设备限制,难以获得全空域RCS数据,且精度低,费用高;第三种是电磁仿真,随着电磁仿真理论和计算能力的提高,特别是电磁仿真软件能力的大幅提升,使电磁仿真成为目标RCS获取的首选方法,但电磁仿真对材料和形状敏感,仿真与真实数据还有一定差距。针对当前电大目标RCS数据获取存在的问题,结合电磁仿真全空域覆盖和雷达实测数据真实有效的优势,采用模型参数调整和实测数据修正相结合的方法,可获取高精度的火箭RCS仿真数据。

文中研究在双频段相控阵雷达上开展,该双频段雷达包括S和X频段两个阵面,可单频段单站或双频段同站工作。首先介绍了电大尺寸目标的电磁仿真技术,采用HFSS软件SBR求解器,对5型火箭进行了双频段RCS仿真;其次研究了目标RCS产生的机理,解算目标视线角与RCS的数学关系,得到了火箭飞行理论RCS序列;再次采用高精度RCS标定技术保证雷达测量RCS精度在0.5 dB以内,通过比较目标理论RCS序列和实测RCS数据,找到了误差产生的主要原因;最后根据主要误差源,提出了模型参数调整和实测数据修正相结合的雷达RCS修正方法,将火箭RCS仿真精度从5 dB提高到2 dB。基于此仿真模型,用测量RCS数据开展飞行器姿态估计,实现了利用外测数据进行火箭目标姿态估计的突破;提出的特征点识别方法在火箭识别上具有明显优势,识别能力得到明显提升。

1 火箭RCS仿真

1.1 HFSS软件SBR求解方法

常用的电磁仿真软件有HFSS、CST和FEKO等,其中Ansys公司的HFSS软件应用较广,求解算法包括:有限元算法(FEM)、积分方程算法(IE)、高频算法(SBR+ solver)[7-8]、混合算法(FEBI,IE-region)、域分解算法(DDM,FA-DDM)、时频算法(transient)、特征模算法(CMA)和本征模求解器(eigenmode solver),其中全修正弹跳射线法(SBR+)是该公司针对复杂结构及超大尺寸问题引入的新算法,是一种通用且高效的电大尺寸问题高频近似算法,弹跳射线法(SBR)混合了几何光学(GO)和物理光学(PO)方法,广泛应用于大场景下目标RCS仿真,“+”是在SBR的基础上对物理绕射效应(PTD)、几何绕射效应(UTD)和爬行波效应(creeping wave)的全精度修正,SBR+支持FEM和IE求解。

火箭是典型的电大目标,RCS仿真采用HFSS软件SBR模式能够提高仿真速度和精度。仿真过程包括物理建模、SBR方法选择、激励设置和仿真计算4步。火箭箭体总长约20 m,直径约1.4 m(三级部分直径略小),β取(子午面张角,文中简称视线角LOS)0°,63.4°,84.5°,90°,99.6°和180°分别正对整流罩上平面、整流罩上斜面、二三级连接斜面、箭体、三级与整流罩连接斜面和底面。为简化SBR仿真,采用绘制线段绕z轴形成曲面的建模方法,电大尺寸非常占用资源,如果圆柱面设置增大、扫描范围增大或扫描步长减小,仿真时间将几何增加。考虑实际精度需要和仿真速度限制,基于提高仿真速度考虑,将圆柱分为36个面,按照1°步长进行仿真。首先进行建模,通过选择建模曲面,设定SBR+算法和仿真频率(采用S和X两个频率分别仿真)。然后进行激励设置,通过激励扫描设置可完成RCS极坐标激励设置,激励设置对计算时间影响较大,基于火箭对称结构将仿真方位向设定为0°,俯仰向按照1°步长从0°扫描至180°,得到俯仰向RCS曲线。最后是模型检查、仿真计算和结果查看。

1.2 火箭双频段RCS仿真

火箭起飞后约80 s一二级分离,出现二级上和一子级2个目标,在二三级分离后二级上将分为三级上和二子级,此后还有三级分离等动作。根据火箭分离动作箭体有5个仿真模型:全箭、二级上、三级上、一子级和二子级,如图1中(a)～(e)所示。

图1 火箭各子级仿真建模图Fig.1 Simulation modeling diagram of each sub-stage rocket

不同频率箭体目标RCS仿真结果如图2所示,各箭体目标RCS仿真数据的特征点(峰值)如表1所示。由表1可知各峰值点对应的角度与前文正对各面的角度一致,说明电大目标的RCS主要由镜面反射决定,峰值大小和对应的角度是判别箭体形状的有效数据,利用RCS数据进行箭体各夹角和面积计算可实现目标大小、形状的估计;同等条件下X频段相对S频段RCS要大5～10 dB,140°低RCS区X频段比S频段低3 dB,说明X频段能够获得更高的RCS对比度,在分辨率上X频段也明显更高;在110°～150°内RCS变化较小,不利于目标姿态估计;三级上由于没有了二级到三级的转换面,在85°时没有峰值,且由于直径减小,在180°时RCS较小;全箭和二级上除在90°有差别外,其他位置变化不大;分析一子级、二子级数据,视线角0°和180°时X频段比S频段大10.3 dB,圆面的RCS反比波长2次方,视线角90°时X频段比S频段大5.1 dB,圆柱侧面RCS反比波长1次方,全箭、二级上和三级上在90°时X频段比S频段大约2～3 dB,此时既受到圆柱体侧面RCS反比波长的影响,也受圆台侧面RCS正比波长的影响。

表1 不同频率火箭各级及子级RCS仿真特征点数据表Table 1 Simulation feature points of rocket RCS in different bands dB

2 飞行目标理论RCS生成

2.1 视线角求解

火箭飞行前可根据理论弹道、目标姿态角和站址坐标计算出α和β,α为弹体坐标系中目标赤道面张角,β为子午面张角,具体定义参看相关坐标系定义[9-10],文中研究对象为Z轴对称结构,不同α下的RCS值相同,因此仅讨论视线角β变化情况。

1)计算测控站在发射坐标系中的坐标

火箭姿态角由发射系定义,计算测控站下的箭体坐标,首先将测控站站址转换到发射坐标系。

(1)

式中:

其中:a为参考椭球长半轴;e为第一偏心率;Lf,Bf,hf为发射原点的大地经纬度和高程;Lc,Bc,hc为测量坐标系原点的大地经纬度和高程;Af为发射方位角。

2)计算测控站在箭体直角坐标系的坐标

(2)

式中:

其中:x,y,z为理论弹道参数;ψ,φ,γ为箭体俯仰、偏航和滚动姿态角。

3)计算α和β

(3)

(4)

2.2 火箭飞行RCS序列生成

飞行目标RCS序列生成流程框图如图3所示,根据箭体结构等参数确定HFSS仿真模型,采用SBR进行单站RCS仿真,得到箭体目标全空域RCS数据。根据理论弹道和姿态信息计算出目标理论α值和β值,用此理论数据查单站目标全空域RCS数据,得到飞行目标的仿真RCS序列。此RCS序列也可用于跟踪距离估算和检测门限设置的输入。

文中仅对火箭一级分离前进行分析。计算火箭3次相近射向飞行的视线角如图4(a)～(c)所示,3次飞行目标视线角变化基本相同。根据前面的分析,确定主要RCS的峰值点在53 s(对应85°)、57 s(对应90°)和63 s(对应100°)。以S频段雷达为例,视线角数据在仿真S频段全空域RCS表中查找对应RCS值,得到3次飞行S频段每秒RCS序列如图4(d)～(f)所示,由于3次飞行理论弹道差别不大,RCS序列曲线具有一致性。

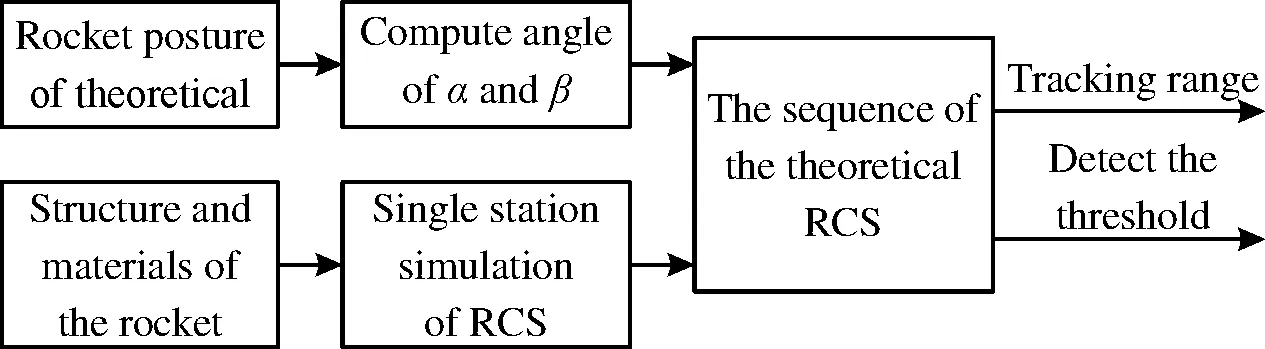
图3 火箭飞行理论RCS序列仿真流程框图Fig.3 Flow diagram of the RCS simulation of rocket ideal flight

图4 火箭同射向飞行视线角和仿真RCS序列曲线图Fig.4 LOS and RCS of rocket in same launch direction

3 实测RCS序列与仿真RCS序列比对

火箭3次同射向飞行平稳,为保证RCS测量数据精度,通过卫星实现雷达RCS的高精度标校[11],标校精度优于0.5 dB。以S频段测量数据为例,3次飞行前80 s测量的RCS序列如图5(a)～(c)所示,雷达的数据率在5～10 Hz变化,为方便比较,采用每秒数据中取最大值的方法将数据率转化为1 Hz,如图5(d)～(f)所示,3次飞行的RCS序列具有相似性。

由图4和图5找到关键特征点并归纳如表2所示,3次弹道基本一致,视线角计算相近,实测RCS数据在各视线角上保持一致,3次飞行特征强相关,相关系数计算均大于0.8,说明实测RCS数据比较稳定,这是采用RCS进行目标识别的基础,同时也说明采用测量RCS序列对仿真RCS数据进行修正具有可行性。实测数据在24 s和39 s有2个峰值点,这2个峰值点与32 s呈对称态,与视线角计算结果相符。仿真结果与实测略有差别,在90°视线角上基本保持一致,说明整体圆柱部分仿真与实际基本一致;在85°、100°和140°视线角上3次飞行数据保持稳定,比仿真数据要大一些,主要原因是火箭建模不够精细,用简单圆柱体代替实际复杂曲面,没有考虑栅格舵等影响;其次是火箭飞行过程中,特别是在火箭飞行与视轴夹角较小时,RCS受火箭火焰影响较大,需要进行修正处理。

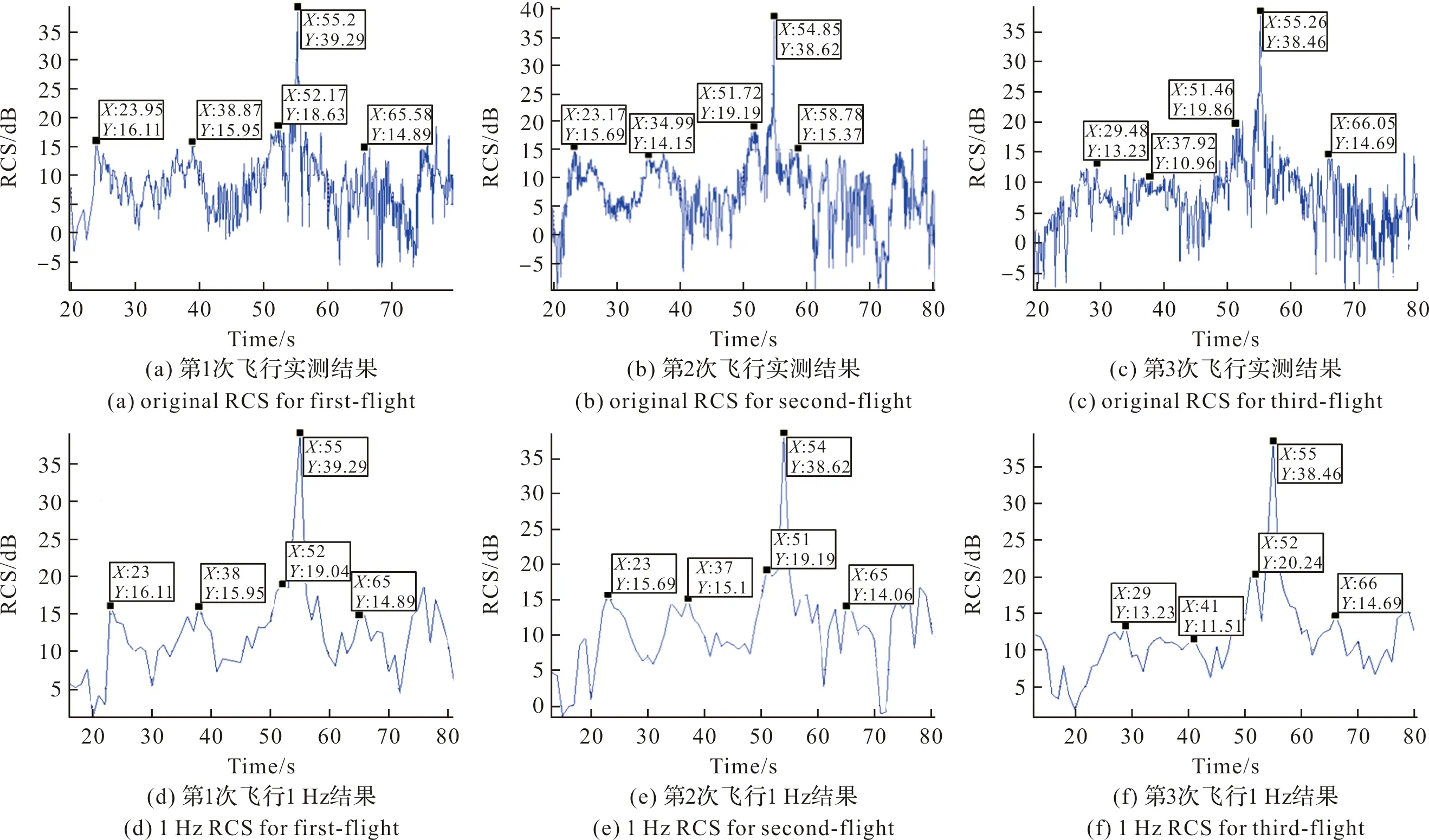
图5 火箭同射向飞行RCS序列实测结果Fig.5 Measured RCS of rocket in same launch direction

表2 3次飞行理论RCS序列与实测RCS序列比对表Table 2 Comparison of the three-flight ideal RCS and measured RCS dB

由雷达测量数据计算视线角,然后得到仿真RCS数据,并和测量RCS数据比对是提高RCS精度的有效方法,同时也推动了利用测量RCS进行飞行姿态估计的研究。雷达作为外测设备,主要的测量元素是定轨参数(距离、速度、方位角和俯仰角)获取,不具备姿态信息获取能力,因此火箭飞行中对遥测的依赖十分严重,一旦火箭飞行异常且遥测无数据,就没有了火箭姿态信息。

4 雷达RCS修正

4.1 单频段RCS修正

电大目标RCS测量包括暗室测量法和动态测量法,无论哪种方法都十分困难,特别是对火箭这样的电大目标,要在暗室中获得其全空域RCS几乎不可能;飞行中目标姿态与雷达视线变化有限,不可能用飞行数据得到全空域RCS数据。为提高仿真精度,提出采用电大目标建模仿真获得全空域RCS数据,然后用实测数据对仿真数据进行修正的方法。该方法有以下优点:一是通过改变模型参数来改变RCS仿真数据,用新的仿真模型得到更加准确的全空域RCS数据;二是考虑真实箭体复杂难以准确建模,火焰等影响难以仿真,可通过测量RCS数据来修正全空域RCS的数据。综合而言,此方法能够在不准确仿真条件下获得真实全空域RCS数据。

表2在85°上实测序列比仿真大4.2 dB,在100°上实测序列比仿真值大3.5 dB,但视线角对应比较好。为研究不同参数对RCS仿真的影响,将二级级间段增加300 mm,末级变罩部分半径增加30 mm,长度增加200 mm,仿真结果如表3所示,按照RCS曲线峰值点给出相应幅度值,调整参数后数据与实测更相近,但对应的角度略有变化,S频段变为62°、86.5°和99°,X频段变为62°、86°和99.5°,说明参数变化影响要结合幅度和角度值综合考虑,参数修正能够获得更加准确的RCS数据。仿真数据表明,X频段与S频段在细节上有明显差别,测量的RCS序列能够准确反映这种差别,这种差别是实现双频段识别的有利因素。实测数据在140°上比仿真结果大约10 dB,原因一方面是实际箭体结构并非光滑曲面,另一方面RCS易受火焰影响,此时采用测量RCS序列对RCS仿真数据进行修正,具有简单有效的特点,能够有效提高全空域RCS数据的准确性。

表3 调整箭体参数后RCS仿真结果Table 3 The RCS simulation results after adjusting the rocket parameters dB

雷达单频段工作模式下的修正流程如图6所示,首先是利用单站测量的位置、姿态等信息得到α和β数值,然后计算出理论RCS序列,通过理论与实测RCS比对,发现存在的问题,分别采取修正箭体尺寸、结构材料的模型修正方法和实测数据修正的方法来提高仿真的准确性,建立火箭较为准确的全空域RCS数据。修正结果表明:不修正时火箭仿真RCS特征点数据误差在5 dB以内,修正后特征点误差在2 dB以内。采用该方法能够用参数估计获得目标尺寸大小、峰值对应角度等重要识别信息,也能够进行相关识别特征的提取,实现识别信息点、线、面的全面利用。

图6 单频段RCS仿真修正流程Fig.6 RCS simulation correction process in single-band

4.2 双频段RCS修正

前文主要以S频段为例研究了火箭RCS的修正方法,双频段雷达具有同站工作模式和异站工作模式。同站模式下双频段测量的α和β及目标都相同,其修正流程如图7(a)所示,首先是利用双频段测量的位置和姿态等信息进行α和β计算,接着计算出理论RCS序列,通过理论与实测RCS比对,采取修正箭体尺寸、结构材料和各频段RCS仿真数据的方法提高仿真的准确性,处于同站工作下可直接采用双频段RCS做差开展精确识别,提高识别的准确性。异站模式下各频段测量的α和β不同,修正流程如图7(b)所示,首先利用各自频段测量的位置和姿态等信息进行各自α和β计算,然后计算出双频段各自的理论RCS序列,通过各自理论与实测RCS比对,用统一模型来统一修正箭体尺寸、结构材料,并利用实测数据修正各自频段RCS仿真数据,异站工作下不同视角获得不同峰值点,减少了数据相关性,双频段RCS的融合应用能够提高识别的准确性。

图7 双频段雷达RCS仿真修正流程Fig.7 RCS simulation correction process of dual-band

4.3 基于全空域修正RCS的火箭识别

常用RCS识别方法是利用均值和方差等统计特征参数实施识别,由于火箭RCS与姿态强相关,RCS统计特征识别方法在火箭识别上效果较差。从前文分析可知,RCS曲线上的峰值是目标姿态和反射面形状的综合反映,将峰值点作为特征点进行识别比RCS均值等统计参数识别有更好的识别效果。利用HFSS仿真和实测数据,对5型火箭进行了RCS仿真和修正,得到了5型火箭修正的全空域RCS数据,将火箭初始段正对箭体(视线角为90°)作为特征点,得到5型火箭该特征点的RCS数据如表4,采用RCS差进行目标识别计算,分S频段、X频段和双频段(按照欧式距离计算)3种情况得到5型火箭的识别热图如图8所示,S频段的平均RCS差为5.0 dB,X频段的平均RCS差为6.7 dB,X频段比S频段的识别能力更强,双频段的平均RCS差为9.4 dB,按照修正前5 dB和修正后2 dB精度计算,S频段识别能力从40%提高到70%,X频段识别能力从50%提高到90%,双频段识别能力从80%提高到100%。其余特征点的识别效率与此类似。

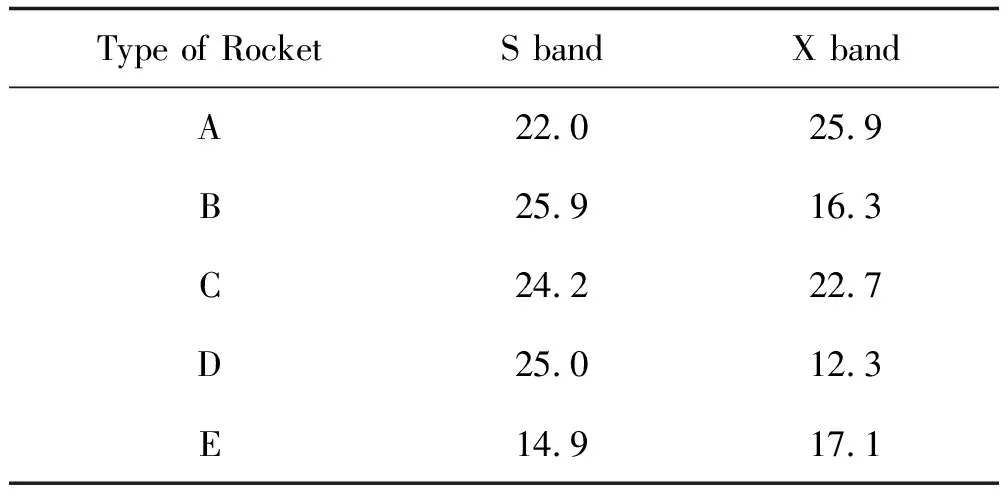
表4 5型火箭视线角为90°时RCS值Table 4 RCS of 5 types of rockets when LOS is 90° dB

图8 不同频段5型火箭RCS差识别热图Fig.8 RCS difference recognition heat map of 5 types of rockets in different bands

5 结束语

文中从火箭RCS仿真入手,研究了火箭电大目标的电磁仿真方法,采用HFSS软件SBR解算实现了5型火箭的双频段全空域RCS仿真,提出了模型参数调整和实测数据修正相结合的修正流程,将RCS仿真精度从5 dB提高到2 dB。基于此仿真模型,用RCS数据开展飞行器姿态估计,实现了利用外测数据进行火箭目标姿态估计的突破。提出的特征点识别方法在火箭识别上具有明显优势,识别能力得到明显提升。

双频段雷达全空域RCS数据获取技术有助于提高对各型火箭目标的识别能力,为后续基于特征点的识别方法向基于特征线和特征面的识别奠定了基础。