NM理论中积分真度的统一理论
王波, 惠小静, 鲁星
(延安大学 数学与计算机科学学院, 陕西 延安 716000)
数理逻辑的特点在于形式化而不是数值计算,为了反映程度化的思想,20世纪50年代初,Rosser教授利用“指派真值”来刻画逻辑公式和反映逻辑推理的真实程度[1],这种思想在Pavelka的系列文章[2]中得到了全面发展。后来有许多学者从不同角度提出了逻辑公式的程度化思想。
21世纪初,王国俊教授在经典二值命题逻辑中引入了命题的真度概念[3],提出了计量逻辑学理论,建立了一套近似推理模式之后,国内外学者展开了广泛的研究,得到了一些重要结果[4-6]。但是以上所有结果都建立在均匀概率测度空间上。为此,文献[7]利用赋值空间上的Borel概率测度在二值命题中引入了公式的概率真度概念。文献[8]在ukasiewicz模糊逻辑系统uk、Gödel模糊逻辑系统Göd、Product模糊逻辑系统Π和R0模糊逻辑系统这4种模糊命题逻辑系统中提出了公式的积分真度概念。文献[9]在一类命题逻辑系统中借助文献[7]的思想提出了利用积分定义公式真度的统一方法。文献[10-11]在SMTL命题逻辑系统中提出了公式的积分真度理论。
本文将文献[8]的思想和方法应用于NM命题逻辑系统中建立了公式积分真度的统一理论。首先,验证了积分真度MP规则、HS规则;其次,引入了积分相似度和积分伪距离;最后,引进了隶属函数和相容度的概念。值得注意的是,首先,文献[8]的结果可纳入到本文更广泛的统一框架下;其次,在NM系统中,文献[9]关于建立积分真度和相似度提出的假设条件全部成立;最后,本文的结果是对文献[10-11]的进一步推广,更加丰富了左连续三角模的模糊逻辑系统计量化研究。
1 预备知识
假设S={p1,p2,…}是可数集,ψ是S生成的自由代数,其中分别为,∨,→一元算子和二元算子。不同的蕴含算子和赋值格决定了不同的逻辑系统,下面介绍幂零极小逻辑NM的蕴含算子和相应的t-范数定义[12]
注1把标准的NM代数称为[0,1]中的NM代数,通常取n(x)=1-x。
定义[0,1]上的二元算子&和→如下
x&y=x⊗ny,x→y=RNM(x,y)
(3)
注2从ψ到R区间[0,1]的(,∨,→)型同态v:ψ→[0,1]称为ψ的R-赋值。
定义1幂零极小逻辑NM系统由以下12个公理模式和推理规则MP组成[13]
MP规则 由A,A→B推出B。
定义2设A=A(p1,…,pn)是ψ中含有n个原子公式p1,…,pn的公式,在A中把pi换成xi并保持,∨与→不变,但把它们理解为R单位区间上相应的运算,则得一n元函数:称是由公式A所诱导的函数[14]。
定义3自然数列u1,u2,…叫斐波那契数列,若u1=u2=1,且un+un+1=un+2(n=1,2,…)[13]。
定义4设⊗是[0,1]上的左连续三角模,在[0,1]上定义二元运算→如下[15]
b→c=∨{x|x⊗b≤c}x,b,c∈[0,1]
则
1) →是⊗与相伴随的蕴含算子,即a⊗b≤c当且仅当a≤b→c。
2)b→c=1当且仅当b≤c。
3)a≤b→c当且仅当b≤a→c。
4)a→(b→c)=b→(a→c)。
5) 1→c=c。
7)b→c关于c单调递增,关于b单调递减。


2 NM理论中的积分真度
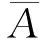
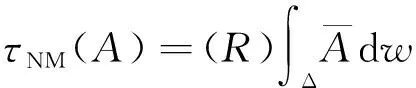
(4)
被称为A的R-真度。
定理1设A∈ψ,则τNM(A)=1当且仅当A是RNM-几乎重言式。
证明若A是RNM-几乎重言式,则τNM(A)=1,反过来,设A=A(p1,…,pn)∈ψ且τNM(A)=1,则

命题1设A∈ψ,则τNM(A)=1-τNM(A)。
推论1设A∈ψ,则τNM(A)=0当且仅当A是RNM-几乎矛盾式。
引理1设f(x,y)=RNM(x,y),则f(a,c)+1≥f(a,b)+f(b,c)。
证明设a≤c,则f(a,c)=1。
1) 设b
f(a,c)+1≥f(a,b)+f(b,c)
设b f(a,c)+1≥f(a,b)+f(b,c) 2) 设a≤b≤c,类似1)的证明。 3) 设c 当a>c时,类似可证f(a,c)+1≥f(a,b)+f(b,c)成立。 综上所述,设f(x,y)=RNM(x,y)时,f(a,c)+1≥f(a,b)+f(b,c)成立。 定理2设→:[0,1]2→[0,1]是二元函数,a,b,c∈[0,1],I为指标集,则 c≥b+b→c-1 证明由引理1可得,RNM(a,c)+1≥RNM(a,b)+RNM(b,c),所以a→c+1≥a→b+b→c,令a=1,则1→c+1≥1→b+b→c,由定义4的第5)条得,c+1≥b+b→c,即c≥b+b→c-1。 定理3(积分MP规则)设A,B∈ψ,若τNM(A)≥α,τNM(A→B)≥β,则τNM(B)≥α+β-1。 推论2设A,B∈ψ,若τNM(A)=1,τNM(A→B)=1,则τNM(B)=1。 定理4(积分HS规则)设A,B,C∈ψ,若τNM(A→B)≥α,τNM(B→C)≥β,则τNM(A→C)≥α+β-1。 证明因为(B→C)→((A→B)→(A→C))是重言式[13],所以由定理1得,τNM((B→C)→((A→B)→(A→C)))=1。因为τNM(B→C)≥β,所以由定理3得,τNM((A→B)→(A→C))≥1+β-1=β,又因为τNM(A→B)≥α,所以再由定理3得,τNM(A→C)≥α+β-1。 推论3设A,B,C∈ψ,若τNM(A→B)=1,τNM(B→C)=1,则τNM(A→C)=1。 命题2假设In=p1∧…∧pn,Un=p1∨…∨pn,是S中不同的原子公式,那么 (5) 例1计算τNM(p→q)和τNM(p→p∨q)的值。 解Δ1={(x,y)|x≤y}, Δ2={(x,y)|1-x>y}, Δ3={(x,y)|1-x≤y}, 定义8设A,B∈ψ,则称 (6) 为A与B之间的R积分相似度。 命题3设A,B∈ψ,则 1)ξNM(A,A)=1。 3)ξNM(A,B)=ξNM(B,A)。 定理5设A,B∈ψ,则ξNM(A,B)=1,当且仅当A与B几乎逻辑等价。 引理2设f(x,y)=RNM(x,y)∧RNM(y,x),则f(a,c)≥f(a,b)+f(b,c)-1。 证明 1) 设a≤c,并且1-c>a时,f(a,c)=1-c; 2) 设a≤c,并且1-c≤a时,f(a,c)=a。 先讨论第1)种情况 ①设b 设b ②设a≤b≤c,类似于①的证明。 ③设c ④对于第2)种情况以及a>c时,类似可证f(a,c)≥f(a,b)+f(b,c)-1成立。 综上所述,设f(x,y)=RNM(x,y)∧RNM(y,x)时,f(a,c)≥f(a,b)+f(b,c)-1成立。 定理6设A,B,C∈ψ,若ξNM(A,B)≥α,ξNM(B,C)≥β,则ξNM(A,C)≥α+β-1。 证明由引理2可得, ξNM(A,B)+ξNM(B,C)-1≥α+β-1 定义9设A,B∈ψ,规定 ρNM(A,B)=1-ξNM(A,B) (7) 定理7ρNM:ψ×ψ→[0,1]是ψ上的积分伪距离。设A,B,C∈ψ,则 1)ρNM(A,A)=0。 2)ρNM(A,B)=ρNM(B,A)。 3)ξNM(A,C)≥ξNM(A,B)+ξNM(B,C)-1。 命题4设A,B∈ψ,当A为定理时, ρNM(A,B)=1-τNM(B) (8) 定义10设A∈ψ,Γ⊆ψ,从Γ到A的准推理是一个有限序列A1,…,An,其中An=A,且对每个i≤n,Ai∈T∪Γ,或者有j,k 命题5设A∈ψ,Γ⊆ψ,A∈D(Γ(n)),如果对每个B∈Γ均有τNM(B)≥α,则 τNM(A)≥un(α-1) (9) 式中,un是斐波那契数列的第n项。 证明证明过程类似文献[14]中的证明,在此不再重复。 注3由(9)式可以看出,当Γ中各公式的真度小于1时,则随着推演长度的增加,所得准推论的真度将减小。 定义11设Γ⊆ψ,令D(Γ)={A∈ψ|(q)Γ 定义12假设A,B∈ψ,那么 div(Γ)=sup{ρNM(A,B)|A,B∈D(Γ)} (10) 称div(Γ)为理论Γ的发散度。当div(Γ)=1时称Γ为全发散理论。 定义13假设Σ是ψ中的非空子集,那么 d(Σ)=sup{ρNM(A,B)|A,B∈Σ} (11) 被称为Σ的直径。 注41) 如果Σ是ψ包含一个定理的有限子集,那么 d(Σ)=1-τNM(A)(A是Σ中最小真度公式) (12) 2)d(Γ(n+2))>d(Γ(n))(n越大,d(Γn)越大) (13) 定理8设A,B是NM中的公式,Γ是NM中的理论,d(Γ(n))-d(Γ(b))=1(A∈D(Γ(n)),B∈D(Γ(b)),b是常数,A的推演长度为n,B的推演长度为b)当且仅当A是矛盾式B是重言式。 证明假设d(Γ(n))-d(Γ(b))=1,根据(12)式及真度的取值范围知,0≤d(Γ(b))≤1,0≤d(Γ(n))≤1。当d(Γ(n))-d(Γ(b))=1时,只有当d(Γ(n))=1,d(Γ(b))=0时等式成立,所以τNM(A)=0,τNM(B)=1,即A是矛盾式B是重言式。 假设A是矛盾式B是重言式,所以τNM(A)=0,τNM(B)=1,由(12)式得,d(Γ(n))=1-τNM(A)=1,d(Γ(b))=1-τNM(B)=0,所以d(Γ(b))-d(Γ(n))=1。 定义14假设A,B是NM中的公式,Γ是NM中的理论,定义 (A∈d(Γ(n)),B∈d(Γ(b))) (14) 并且 「d(Γ(n))-d(Γ(b))⎤= (15) 称i(Γ)为NM中理论Γ的极性指标。 定义15假设Γ是NM中的理论,那么 (16) 称ζ(Γ)为NM中理论Γ的相容度。(i(Γ)是由上述定义14给出)。 证明假设A1=p2,Ak=p1→Ak-1(k=2,3,…),p1,p2是不同的原子公式,并且(v(p1)=x1,v(p2)=x2),根据(2)~(3)式得 所以 因此 所以 定理10假设Γ是NM中的理论,那么 1)Γ是相容的当且仅当i(Γ)=1。 2)Γ是不相容的当且仅当i(Γ)=0。 证明假设Γ是不相容的,那么Γ├C(C是矛盾式),因此C∈d(Γn)∈D(Γ)。因为每个理论都包含定理,所以A∈d(Γb)∈D(Γ)(A是重言式)。因此得,d(Γ(n))-d(Γ(b))=1,所以i(Γ)=0。另一方面,假设i(Γ)=0显然成立,因此(2)式成立,(1)式自然也成立。 定理11假设Γ是NM中的理论,那么 1) 如果i(Γ)=0,则div(Γ)=1,但反之不成立。 2) 如果div(Γ)<1,则i(Γ)=1,但反之不成立。 证明假设i(Γ)=0,根据定理10得,Γ是不相容的,根据(10)~(12)式知,div(Γ)=sup{pNM(A,B)}=1。另一方面,假设div(Γ)=1,即理论Γ是完全发散的,但不能推出Γ是不相容的,即i(Γ)=0,令Γ=S是由所有原子公式构成的,见文献[18],知Γ=S是完全发散并且是相容理论。根据定理10知,当理论Γ是相容时,i(Γ)=1,因此div(Γ)=1不能推出i(Γ)=0。因此(1)式成立,(2)式自然也成立。 定理12假设Γ是NM中的理论,那么 1)Γ是完全相容的,当且仅当ζ(Γ)=1。 2)Γ是不相容的,当且仅当ζ(Γ)=0。 证明 1) 假设Γ是完全相容的,显然成立。假设ζ(Γ)=1,,如果Γ不是完全相容的,那么Γ就有2种情况,第一种情况是Γ是相容的,那么div(Γ)≠0,由定理10的第1)条知,i(Γ)=1,所以由(16)式知,ζ(Γ)<1,另一种情况类似可证明成立。 2) 假设Γ是不相容的,显然成立。假设ζ(Γ)=0,则由(16)式和div(Γ)≤1知,i(Γ)≤0,因为i(Γ)∈{0,1},因此i(Γ)=0,由定理10的第2)条知,Γ是不相容的,因此(2)式成立。 例2假设Γ是NM中的理论,现有理论Γ中的3个公式分别为A,B,C,它们的真度分别为τNM(A)=0.6,τNM(B)=1,τNM(C)=0.7,试比较理论Γ1={A,B}的相容度与理论Γ2={B,C}的相容度大小关系。 注5例2的结果验证了定义的相容度具有合理性。 本文在NM系统中首先引进了积分真度的概念,验证了积分真度MP规则、HS规则,其次利用积分真度的概念引进了积分相似度和积分伪距离的概念,并验证了它们之间的一些性质,最后引进了极性指标与相容度的概念,验证了完全相容理论的相容度为1,不相容理论的相容度为0。
3 NM理论中的积分相似度



4 NM理论中的积分伪距离
5 NM理论中的积分相容度
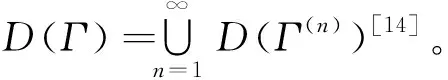

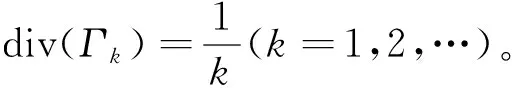
6 结 论

