适用于部分试验数据缺失的气动参数辨识方法
刘洋, 李春娜, 方远, 龚春林
(西北工业大学 航天学院, 陕西 西安 710072)
气动参数辨识是提取飞行器气动参数、预测飞行状态的一种手段,在外形设计、飞行轨迹预测、弹道重构、射表编制等过程中起着重要作用。气动参数辨识可分为在线辨识和离线辨识。在线辨识是在飞行中进行参数辨识,目的是预报飞行状态和进行自适应控制。离线辨识是在飞行试验后进行参数辨识,目的是建立准确的“气动参数-运动状态”数学模型,同时包含模型辨识和参数辨识。模型辨识是在一系列候选模型集中选择出与系统输入-输出特性最匹配的数学模型[1],参数辨识是优化所选数学模型中的参数。
离线辨识中,给定试验数据并确定数学模型之后,气动参数辨识问题就转化为最优化问题,设计变量为飞行状态初值和气动参数,目标为最小化计算弹道和测量弹道之间的误差。根据试验数据数量的不同,可分为单条和多条试验数据气动参数辨识。
单条试验数据气动参数辨识发展成熟,重点研究不同飞行器的建模及算法匹配[2-4]。文献[5]对比了输出误差法(OEM)和两步法(2SM)在飞机气动参数辨识中的表现,结果表明OEM更准确,但2SM效率更高更灵活。文献[6]利用极大似然法(MLE)对飞机操稳特性大导数进行辨识,并与小扰动理论分析法进行对比,结果表明随机噪声对大导数的影响较小,但对长周期和滚转模态响应值影响较大。文献[2]提出了对飞行器扰流片参数辨识的元优化算法(MO)及初始样本选取方法,并对比了差分进化算法(DE)等其他9种算法,结果中仅有DE、MO和蚁群算法收敛至全局最优解。
多条试验数据参数辨识方法重点研究多条试验数据间的关系。因为针对飞行数据的气动参数辨识通常存在局限性、差异性和矛盾性。局限性表现为在单条试验数据的辨识中,所得结果仅对当前测量数据有效;差异性表现为受飞行器个体差异、环境、测量等影响,不同数据及其辨识值本身存差异;矛盾性表现为局限性和差异性会互相放大,从而无法将辨识值直接用到其他飞行试验上时。因此,按照这3种特性处理方式的不同可分为2类:①每条试验数据单独辨识,对多个辨识结果取平均值并进行符合修正,作为多条试验数据辨识结果;②同时对多条试验数据进行辨识,获得唯一的辨识结果。
第一类辨识方法原理简单,方法成熟,计算效率高,是射表编拟的标准方法,目前得到广泛应用。文献[7]使用极大似然法对8条导弹靶道试验数据进行辨识,利用辨识结果的均值分析非对称导弹的运动特征。文献[8]利用自适应扩展卡尔曼滤波和Modified Bryson Frazier Smoother(MBFS)对战略导弹的7条试验数据进行降噪,然后利用MLE和Broyden Fletcher Goldfarb Shanno(BFGS)对数据分别进行辨识,所得结果趋势一致,但在数值上仍有较大差异。此类辨识方法存在的主要问题有3个:①可能使用多个数学模型进行辨识[8],不同模型会有不同简化,增大了差异性; ②辨识结果误差较大且可能有偏[7],没有完全解决矛盾性;③部分气动参数难以辨识[7-8]。
在第二类方法中,根据飞行器及试验类型的不同,建模方法不完全相同。文献[9]将再入体的气动参数表示为马赫数和攻角的多项式,同时对9条测量数据进行辨识,所得结果与对相似飞行器的其他研究一致。文献[10]建立了联合雅克比矩阵,并使用梯度法对2种外形相似导弹的4条测量数据进行了辨识。结果表明,同时辨识4条测量数据比同时辨识1条或2条测量数据时目标函数值更小;使用标准模型获得的目标函数值比使用简化模型更小。文献[11]使用差分进化算法对炮弹的6条纸靶试验数据同时进行辨识,辨识结果的精度比第一类方法更好,更能反映实际飞行状态。相比第一类方法,第二类方法的计算成本更高,对试验数据的要求也更高,但能较好地解决辨识的局限性、差异性和矛盾性,所获的气动参数更能反映飞行器实际飞行状态。
在实际工程中,测量系统制约了气动参数辨识的发展。受限于传感器的安装空间、采样频率、测量精度等问题,试验中常有部分飞行数据无法测量或测量误差较大等问题;在部分试验中,测量数据仅能用于制导控制,无法用于气动参数辨识。以上问题存在于各类飞行器的气动参数辨识中,例如飞机[12]、导弹[13]等,增加了辨识难度,降低了辨识准确度,最终限制了飞行器设计。
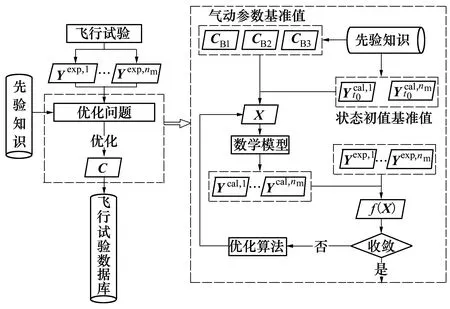
针对测量系统中存在的问题,本文根据第二类多条试验数据辨识方法的基本原理,提出了一种适用于试验数据缺失的气动参数联合辨识方法。该方法先构建包含所有气动参数的飞行器运动模型,以气动参数插值表及状态初值为设计变量,以数值计算数据库、风洞试验数据库及第一类辨识方法所得结果为先验知识,获得一个或多个设计变量基准值,并生成设计空间,利用差分进化算法同时对多条试验数据进行辨识。针对部分飞行状态无测量数据的情况,将气动参数的先验知识与已有测量数据相结合,拟合出第一个测量点处的基准值,将其作为设计变量进行优化。该方法能解决并主动利用气动辨识的局限性、差异性和矛盾性,以获得符合全部飞行数据的全局最优解。将以上方法应用于某子弹多条仿真数据的气动参数辨识中,并与现有方法进行对比,以检验所提方法的正确性和有效性。
1 单条试验数据辨识方法
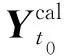
(1)
图1为优化流程,具体介绍如下:
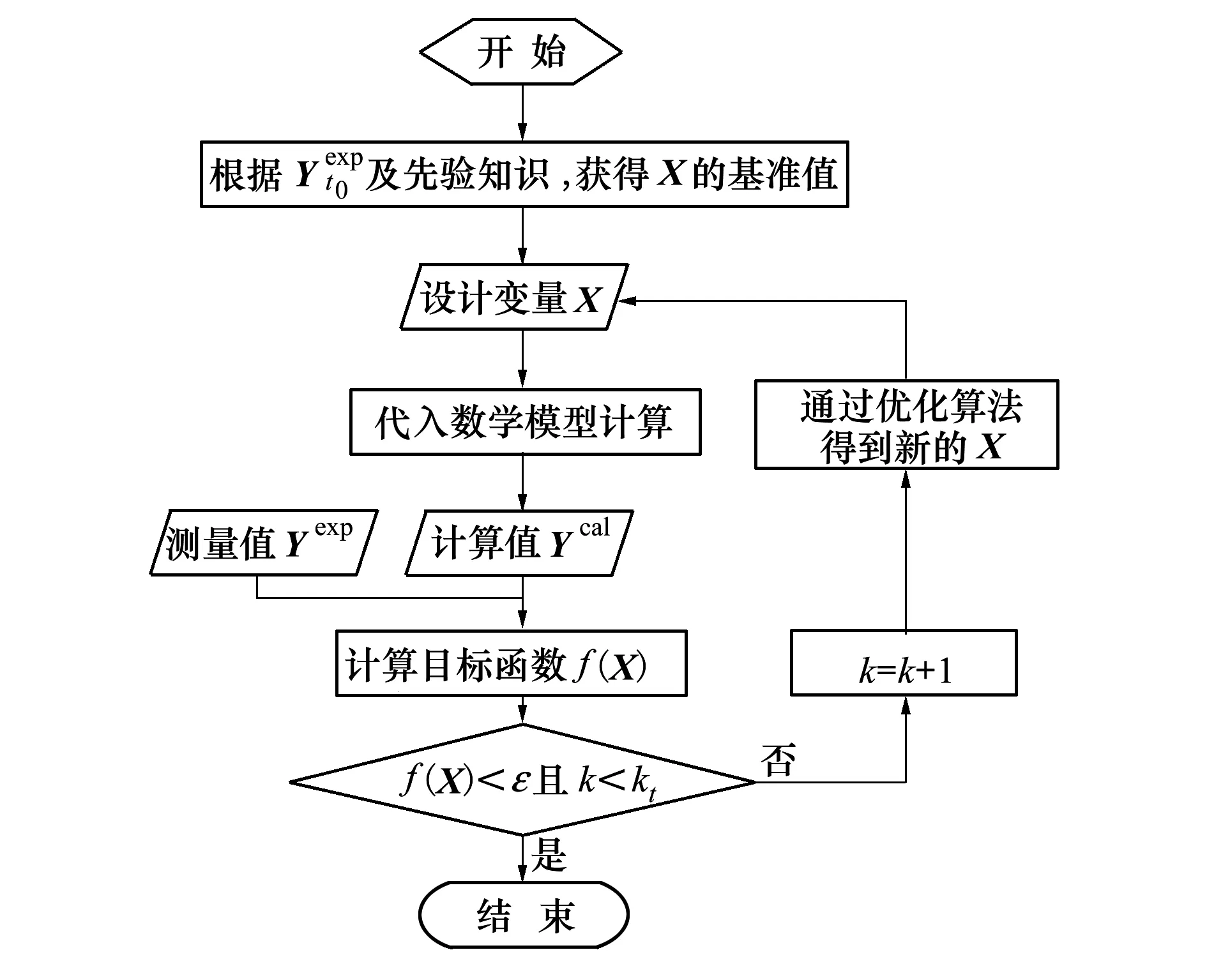
图1 单条试验数据优化流程
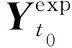
2) 根据试验数据类型、长度、采样频率,确定收敛指标ε和总迭代次数kt;
3) 将X代入数学模型中计算并得到飞行数据计算值Ycal。对于无控飞行器及开环辨识的有控飞行器,该数学模型为飞行器运动方程组,对于闭环辨识的有控飞行器,该数学模型为飞行器运动方程组及反馈回路;
4) 根据计算值Ycal和测量值Yexp计算目标函数f(X);
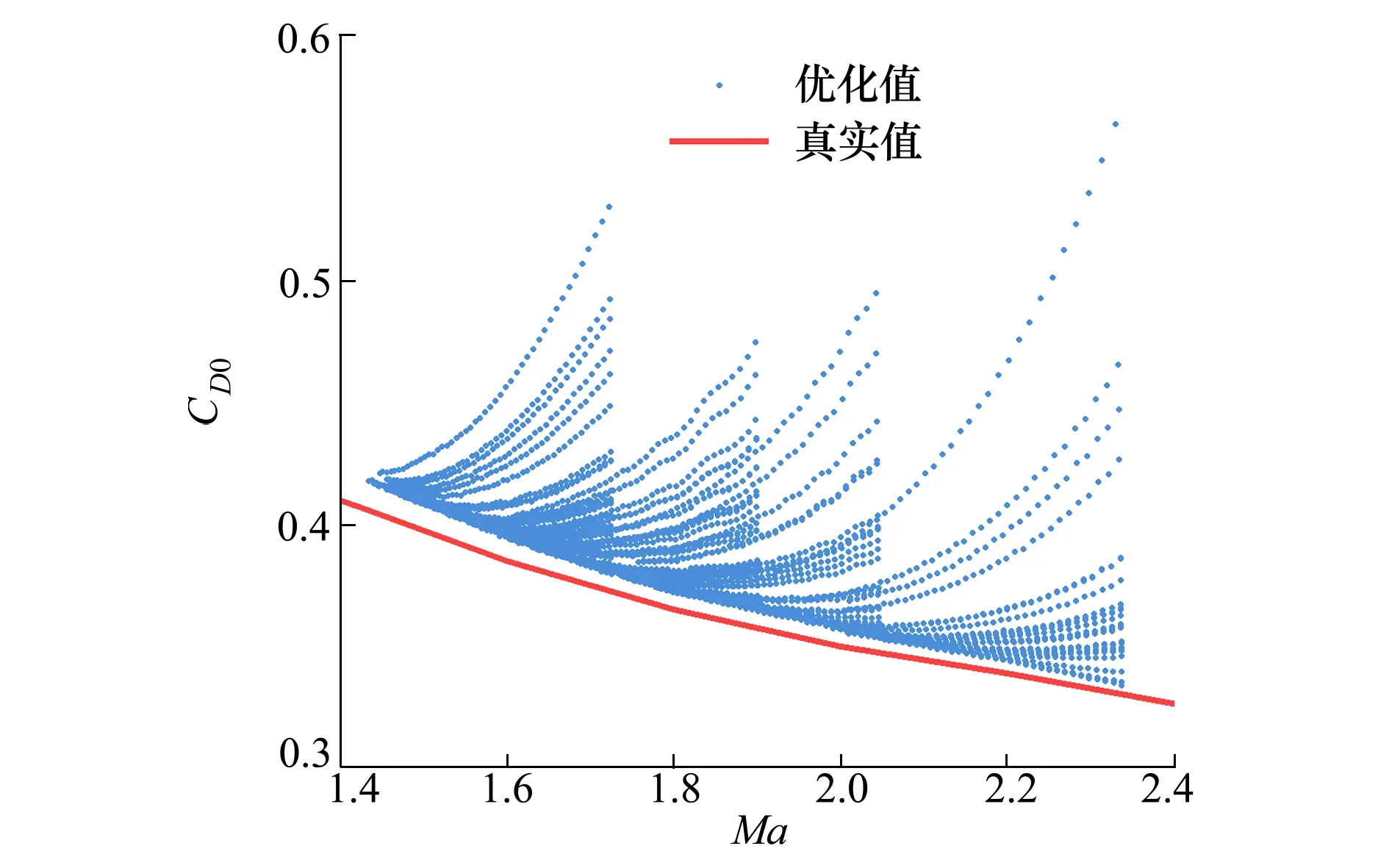
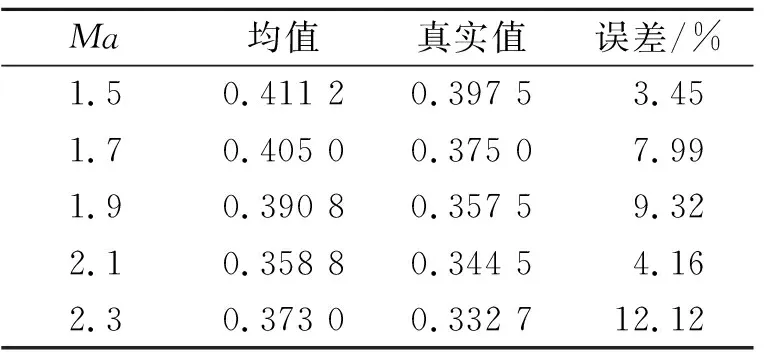
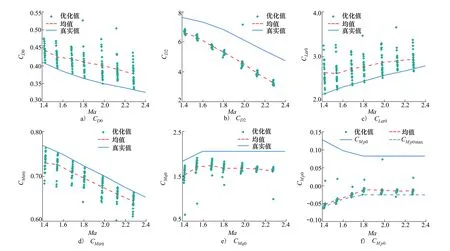
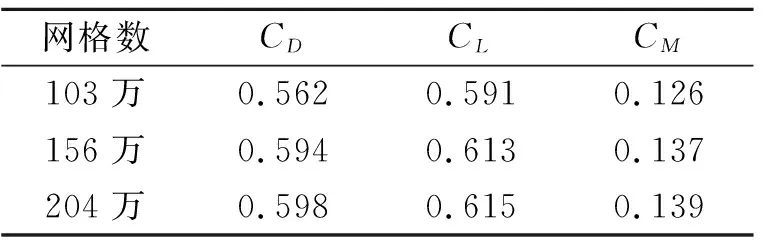
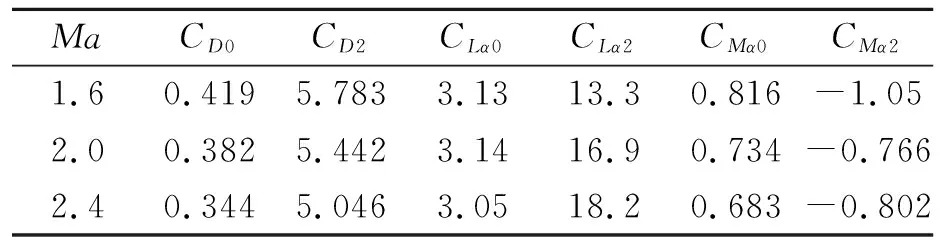
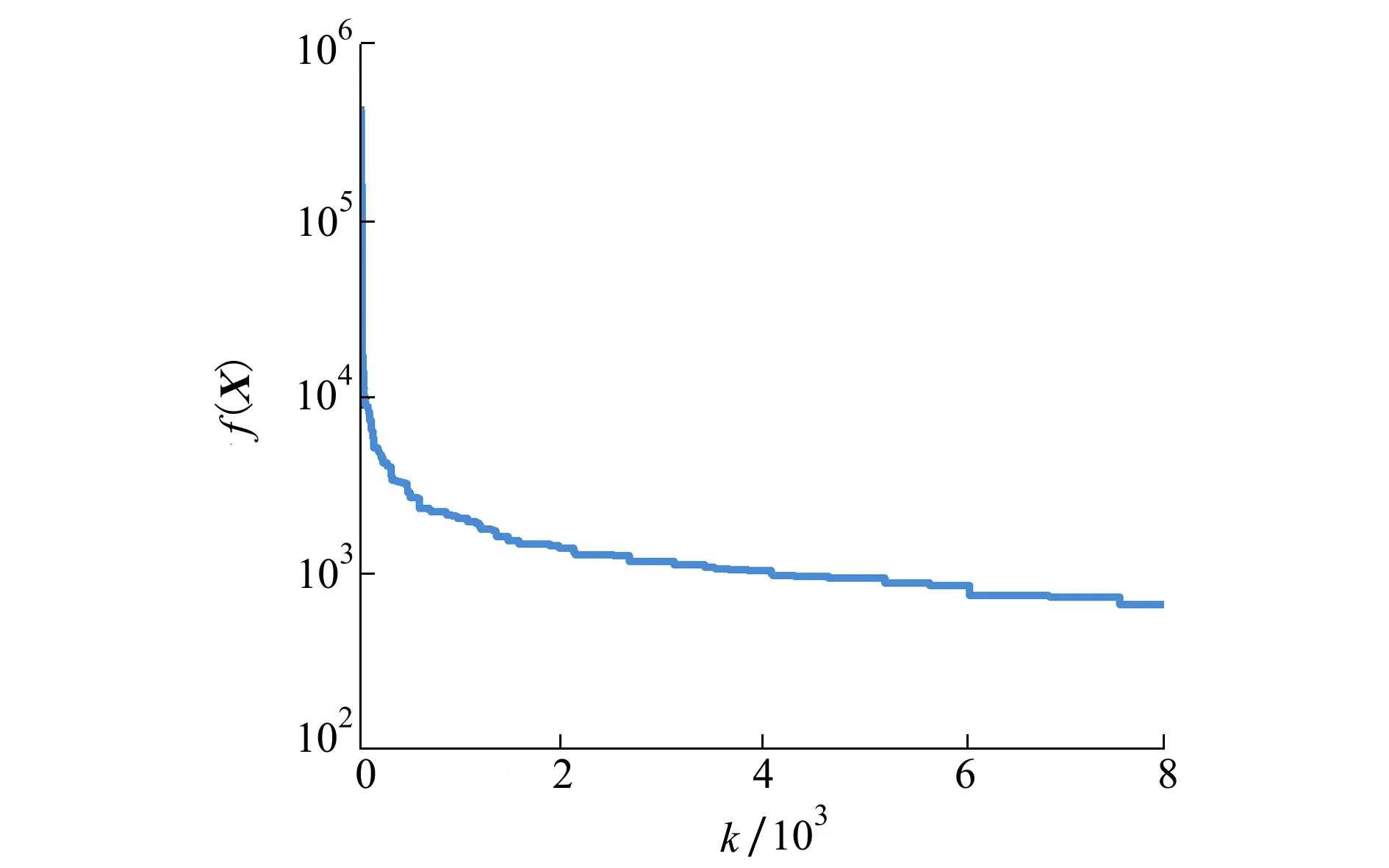
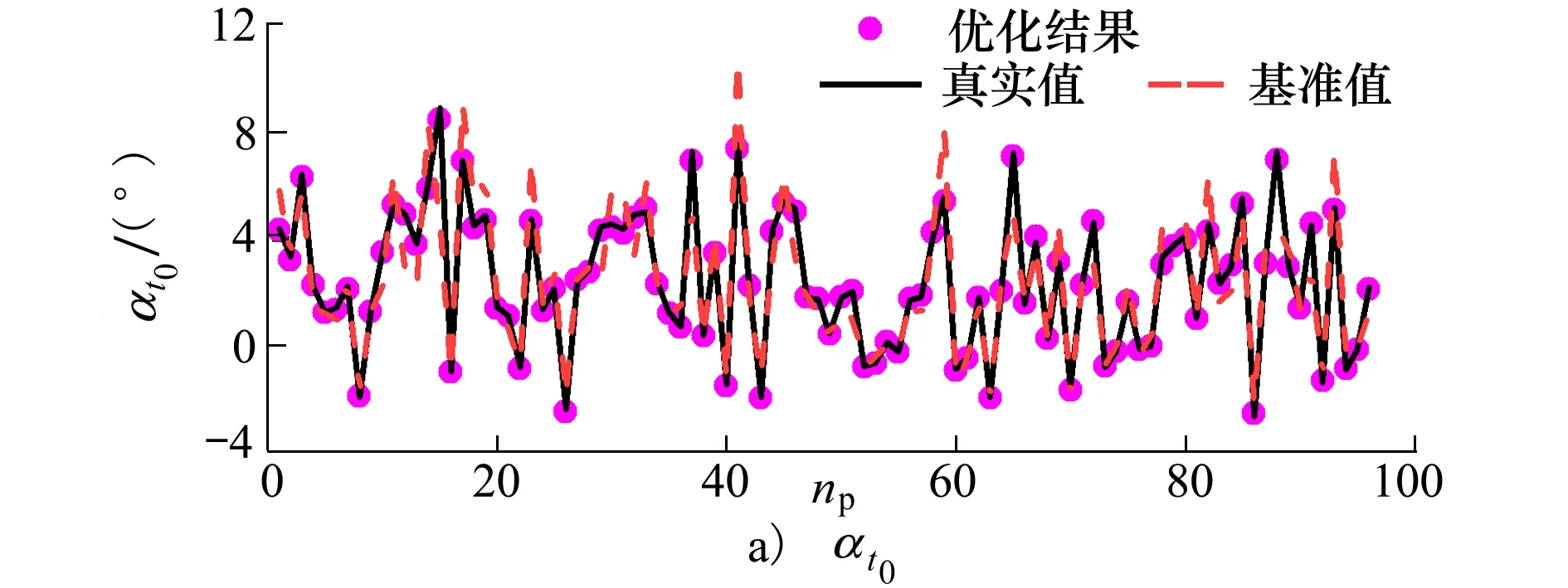
5) 若f(X)>ε且当前迭代次数k (2) 式中:CD0为零升阻力系数;CD1和CD2分别为阻力系数一次项和二次项;o(sin3αt)为更高阶项;CD0,CD1和CD2仍为Ma的函数。由于Ma随时间不断变化,需要分段辨识。 一条试验数据共包含nd个测量点,将其分为ns段,每段包含nf个测量点,相邻两段的测量点可以重复。nf的选取不能过大或过小,若nf小于设计变量个数,噪声对优化的影响较大且优化结果不唯一,若nf过大,则该段Ma可能变化过大。根据图1,每一段试验数据单独构成一个优化问题,其优化结果为该段平均Ma下的设计变量。 与一般优化问题不同的是,f(X)不能完全反映X与真实值的接近程度。将数据分段后,优化受测量误差、模型简化等影响更大,当f(X)很小但X与真实值相差较大时,优化结果不能反映该飞行器的普遍飞行情况,一旦工况发生改变,所得飞行状态与实际可能相差很大。 飞行试验往往是一类多组、一组多次地进行,同组试验工况相同,同类试验的测量系统相同,不同类试验的测量系统、数学模型均可能不同。 (3) 该方法的误差来源主要有以下3个方面: 1) 在每个优化问题中,实际Ma和平均Ma有一定差异,当采样频率较低或Ma变化率较大时,可能导致低灵敏度设计变量辨识误差很大; 2) 不同试验的可测数据与选用数学模型可能不同,对同一气动力、力矩的简化程度不同,因此优化结果在总体上可能是有偏的[14]; 3) 部分飞行试验会使用解耦模型,耦合程度不同,解耦带来的模型误差也不同,使同一气动参数的辨识误差较大。 第一种误差可以通过提高采样频率或忽略低灵敏度的设计变量降低对优化的影响[15],后2种误差无法规避,误差大小受测量数据、设计变量、采样频率、测量噪声、气动非线性等因素的影响,难以定量甚至定性分析。因此,该方法常结合风洞试验数据进行修正[16],或进行符合计算才能应用。 (4) 式中:μi为权系数;nc为μi所属试验类型的总数,目的是f(X)对各类试验的灵敏度相差不会过大;nw为nm条试验数据中的所有测量点 (5) 相比于现有多条试验数据辨识方法,该方法主要做出3点改变: 1) 设计变量X中C的形式与弹道仿真完全相同。在现有气动参数辨识方法中,设计变量是对应平均Ma下的C,但在弹道仿真中,C由当前Ma插值得到。由于C最终提供给弹道仿真使用,为使气动参数更准确,在联合辨识中将C对Ma的插值表作为设计变量,使参数辨识和弹道仿真中飞行状态计算方法完全相同,减小了因气动参数使用方式带来的误差。 2) 将nt条试验数据作为一个优化问题,使用同一个运动方程组进行优化。在不考虑非典型力、力矩的情况下,最能描述飞行状态的数学模型是包含全部气动力、力矩的六自由度模型。在联合辨识中,使用该模型同时对所有测量点进行辨识,所得X能反映试验的所有飞行状态,消除了气动参数辨识的局限性和差异性。 公式(4)中优化问题的维度很高,且C的储存形式为插值表,难以求解梯度信息,在计算资源充足的条件下选用无梯度的差分进化算法作为优化算法。该算法适用于非线性问题,全局搜索能力较强,其种群的求解可以并行以提高计算效率,且在气动参数辨识中的表现优于其他启发式算法[2]。 在联合辨识方法中,初始设计空间对计算准确性和效率有显著的影响。在剔除数值计算数据库、风洞试验数据库和现有辨识结果中不合理的数据后,Cmax和Cmin分别为3个数据库中出现的最大值和最小值,因此设计空间的边界[Clow,Cup]为 (6) 式中:c1,c2分别为上、下界放大系数,不同气动参数的c1,c2不同,需根据具体问题进行分析。 ω和Θ的测量方式包括陀螺仪、地磁传感器、太阳方位传感器、闪光阴影靶道等,但数据并不总能返回地面[10]。当测量数据包含ωt0和Θt0时,可根据测量仪器的系统误差和随机误差得到设计空间;当测量数据有滚转角速度γ′,但不包含其他姿态角数据时,可以根据现有数据库拟合出αt0,αt1和βt0,βt1,再进行微分得到ωt0,最后根据拟合精度和求导精度得到设计空间;当没有滚转角γ时,可根据飞行器类型及典型飞行弹道判断其γt0;当无法判断时,可认为γ=0°,γt0的设计空间为[0°, 359°];对于旋转弹来说,可通过公式计算出口转速γ′ (7) 式中:v0为表定初速;η为膛线缠度。该公式在工程中较准确,但受膛线磨损、发射药温等影响,可能会有一定偏差。 由于传统方法优化结果可能有偏,(6)式生成的初始设计空间不一定包含真实值,因此在生成第一代种群后,不对设计空间的边界进行约束,使搜索可以在边界外进行[11]。在迭代中,由于f(X)是多个‖Ycal-Yexp‖的加权和,因此在计算Ycal的过程中就判断子代是否优于父代,而不必等该个体完全计算完。即每计算完1条试验数据,数据就计算1次f(X),若子代f(X)大于父代f(X),则直接跳出计算,能提高计算效率。 在该设计空间内,以飞行稳定性为约束条件,对公式(4)中的问题进行优化,具体优化流程见图2。 图2 联合辨识优化流程图 1) 根据现有多条试验数据辨识方法,对nm条试验数据进行优化,得到nt个优化结果; 3) 根据气动参数的先验知识,生成3个基准值CB1,CB2和CB3,相互补充并生成C的初始设计空间; 5) 根据试验的可信度和类型占比,选取合适的μi; 6) 将X代入数学模型,判断是否满足稳定性约束并计算出Ycal,并根据(4)式计算f(X); 7) 判断优化是否满足收敛条件,若满足,跳转至8),若不满足,通过优化算法得到新的X,并重复5)~7); 8) 计算结束,X即为优化结果。 图2中,CB1,CB2和CB3分别为数值仿真数据、风洞试验数据和现有方法辨识值。考虑到仅用一种方法难以获得全部的气动参数,因此3个基准值相互补充。 为验证本文所提方法的正确性,对Sierra的7.62 mm竞技子弹仿真数据应用多条试验数据联合辨识方法进行优化。该公开数据包含0~2.5Ma范围内11个气动参数[17],历经多次试验和比赛验证。该仿真数据有5个重要特点: 1) 仿真对象转速高,马格努斯效应强,提高了低灵敏度设计变量的灵敏度; 2) 在全弹道上,ω和γ均不可测,α和β在长距离上难以测量,但在短距离内可测; 3) 可在试验中调整αt0和βt0,使不同试验的飞行状态差异较大; 4) 不包含推力、科式力、闭环控制系统,数学模型的输入-输出仅体现其气动特性; 5) 测量系统的系统误差容易标定; 该子弹速度衰减快、角运动频率高,试验数据的采样频率相对较低,在气动辨识上难度较大。该子弹的运动模型如下: v2PTα-vPθ′) (8) 式中:vx,vy,vz分别为地面系下的速度3分量,x,y,z分别为地面系下的飞行器位置,ρ为大气密度,S为参考面积,l为参考长度,d为弹径,m为质量,Ix和Iy分别为极转动惯量和赤道转动惯量,CLα0和CLα2分别为升力系数导数常数项和二次项,CMα0和CMα2分别为静力矩系数导数常数项和二次项,CMpα,CMpα0,CMpα2和CMpαmax分别为马格努斯力矩系数导数、常数项、二次项和最大值,CMqα为赤道阻尼力矩系数导数,Clp为滚转阻尼力矩系数导数,wx和wz分别为纵风和横风,vr为相对于风的速度,α′和β′分别为角速率。 使用六自由度刚体弹道方程组生成264条仿真数据,其中长距离飞行射程为150 m,有4个初速v0,每个v0有4个射角θ0,每个θ0有6个起始攻角和角速度,共96条数据;短距离飞行射程为10 m,共7个v0和4个θ0,每个θ0有6个起始攻角和角速度,共168条试验数据。对于长距离飞行数据,其测量方式为弹道跟踪雷达,仅有v和R的测量数据。对于短距离飞行数据,为方便研究,选择每0.5 m得到1个测量数据。测量噪声服从正态分布(μ,σ),具体参数设置如表1所示。 表1 仿真参数设置 在长距离飞行试验中,采样间隔为1 ms,对于小口径子弹,更大的采样间隔可能会导致计算发散;在短距离飞行试验中,由于照相机的位置固定,采样间隔为0.5 m,其数学模型转换遵从(9)式 (9) (9)式中将测量数据对t的微分转为对x的微分,使其积分步长为整数。 采用现有多条试验数据气动参数辨识方法对全部试验进行辨识,优化算法为极大似然法。 长距离飞行试验中无攻角数据,因此设计变量C中仅包含CD0,优化结果如图3所示。优化得到的CD0误差较大。但是,优化值均大于真实值,且攻角越大误差越大,相对误差最大的点αt=14.63°。根据文献[1]中的方法求CD0的均值并与真实值对比,结果如表2所示。 图3 长距离飞行试验优化结果 表2 CD0均值 表2中最大误差为12.12%,其余Ma下的误差均小于10%。需要注意的是,由于飞行数据是仿真数据,为充分研究不同攻角的影响,起始攻角从大到小均有分布,但在实际飞行中,很可能所有的起始攻角都较大,这会导致均值与真实值相差很大。 短距离飞行试验中包含α和β的数据,设计变量C={CD0,CD2,CLα0,CMα0,CMqα,CMpα}。CLα2和CMα2的敏感度较低,若将其作为变量,会使优化结果严重偏离真实值[14]。由于xt0=1 m,nd=19,因此无需分段,设置ns=1,nf=19,nt=1 008。优化结果如图4所示。 图4 短距离飞行数据优化结果 从图4中可以看出,优化结果在趋势上正确,但数值相差较大,难以直接使用。CD0均值的最大相对误差为14.17%,最小为8.14%,均大于表2中的优化结果,但未出现误差非常大的解;CD2的优化结果很集中,仅1个离群点出现在1.986Ma。CLα0的分布与CD0相似,均值的最大相对误差为1.423 2Ma下的21.63%,其余Ma下误差均小于16%。 CMα0是所有优化结果中误差最小的,其均值的误差均在5%以下。但需要注意的是,系统误差对CMα0的影响很大,在实际工程中要尽可能地消除此误差。CMqα的灵敏度并不高,均值的最大误差为25.57%,其余误差均小于20%。由于CMqα是非定常气动力系数,由赤道阻尼力矩和下洗力矩构成,难以通过其他方式获取准确的值,因此气动辨识是获得准确CMqα最重要的手段。 在弹道中,CMpα基本达到限幅,CMpα的优化结果相比于CMpα0更接近CMpαmax,但CMpαmax难以使用极大似然法辨识,一般通过拟合得到。综合来看,辨识值均是有偏的,主要有以下2点原因: 1) 数学模型为简化模型。在长距离飞行试验中,仅对CD0进行辨识,会使结果中包含其他气动参数的影响,该影响与攻角呈正相关。由于攻角不为0,因此虽然理论上CD0与攻角无关,但辨识值有偏且取平均无法消除。 2) 气动参数相互影响。如CD0与CD2共同构成了阻力系数,因此容易出现一个增大一个减小的情况,因此结果是有偏的。 总体上,现有辨识方法在缺少部分试验数据的条件下,所得结果误差较大且无法获得全部的气动参数,在实际工程中直接使用会有较大的误差。 使用CFD方法对的关键气动参数进行计算。网格为结构化网格,第一层附面层高度为10-6mm,求解器为Fluent的密度基求解器,湍流模型为k-ω的SST两方程模型,气体为标准理想气体模型。分别对3种网格进行网格无关性验证,计算工况为Ma=1.6、α=10°,所得结果如表3所示。 表3 网格无关性验证 从表3中结果来看,156万网格和204万网格计算结果相差很小,而103万网格与156万网格相差较大,尤其是俯仰力矩系数相差8%。综合计算精度和计算效率,选取156万网格进行CFD计算,其表面网格如图5所示,计算结果如表4所示。 图5 7.62 mm子弹表面网格 表4 CFD计算结果 结合试验数据的优化结果及CFD计算结果,根据设计空间生成方法,在剔除远离其他优化结果的几个解后,获得C的初始设计空间。CLα2和CMα2仅有CFD数据,因此取CLα2和CMα2的最大值的1.5倍为上界,最小值的0.5倍为下界,获得初始设计空间。CMpα0和CMpαmax的初始设计空间相同,而CMpα2通过图4c)中同一Ma下不同CMpα的拟合,给出一个较大的设计空间。该优化问题的约束为 (10) 式中:Sg为陀螺稳定因子,P为转速项,M0和M2为静力矩项,具体计算方法见(8)式。由于C的形式是插值表,且γ是时变的,因此无法在获得新的样本时检验是否满足约束,仅能在弹道计算中进行检验。若不满足则使用罚函数法构建目标函数并跳出当前计算 (11) 式中:c3为惩罚因子。 对于差分进化算法,设置代数kt=8 000,种群数目N=4 900,交叉概率和变异概率因子均为0.8,种群初始化方法为随机拉丁超立方。优化过程的收敛性曲线如图5所示。 图6 目标函数收敛曲线 从图5中可以看出,f(X)在k=8时比k=0时减少了1个数量级,但之后f(X)的下降速度逐渐变慢。由于优化问题的非线性很强,在优化前期,敏感度较高的设计变量最先接近真实值,使f(X)大幅度下降,但在优化中后期,数百个敏感度较低的设计变量是优化的主要对象,因此优化效率降低。 图7 长距离飞行试验αt0和βt0优化结果 从图7中可以看出,αt0和βt0基准曲线在趋势上较为准确,这是f(X)能收敛的重要原因。优化结果的误差大部分在3%~8%,最大误差为10.4%,由于该参数的灵敏度较低且缺少测量数据,该优化结果可以接受。气动参数C优化结果如图8所示。从图8中可以看出,联合辨识方法的优化结果远好于文献[1]中优化方法所得结果。CD0和CMα0最大误差仅为0.43%和2.8%,理论上,v对CD0的灵敏度最高,α和β对CMα0的灵敏度最高,且数学模型精度很高,因此CD0和CMα0的优化结果最准确。 CD2最大误差为10.4%,CLα0和CLα2的最大误差分别为5.1%和8.5%。由于在v的计算中这3个气动参数与α和β有关,因此准确度比CD0低。 CMα2的最大误差为6.7%且趋势与真实值完全一致。CMqα曲线规律较弱但误差较小,这是因为CMqα起抑制角运动的作用。理论上α和β的衰减越明显,优化结果越好,短距离飞行试验的α和β衰减量较小,长距离飞行试验中,v对CMqα的灵敏度很低,因此优化结果规律性较差。 由于子弹转速非常高,马格努斯效应很强,因此CMpα0,CMpα2和CMpαmax的辨识结果较好。在大部分的飞行数据中,CMpα均达到限幅,即CMpα=CMpαmax,因此CMpαmax的优化精度最高,最大误差仅为3.3%,CMpα0和CMpα2需小攻角飞行数据才能得到准确的优化结果,但攻角越小,f(X)对CMpα的灵敏度越低。理论上,γ′越大或α′和β′越小,CMpα的灵敏度越高,因此想得到更精准的CMpα0和CMpα2非常困难,需专门设计针对性试验。 由于Clp对应的飞行状态γ′不作为可测数据,现有方法在该情况下无法进行辨识。Clp仅能通过γ′的衰减获得,短距离飞行试验中γ′几乎没有变化,而长距离飞行数据v对γ′的灵敏度非常低,因此Clp辨识结果最大误差达到了12.7%,但规律正确。 图8b)、8h)、8i)中初始设计空间没有完全包含真实值,这说明联合辨识方法有能力在初始设计空间不包含真实值的情况下,得到接近真实值的优化结果。 本文提出了一种适用于试验数据缺失的气动参数联合辨识方法,并给出基准值及初始设计空间的获取准则。利用7.62 mm子弹仿真数据对该辨识方法进行验证,并与现有多条试验数据辨识方法进行对比,得出以下结论: 1) 在11个气动参数中,极大似然法可以获得6个气动参数。相比于现有方法,联合辨识方法在满足约束的条件下,使用同一数学模型对多条不同类型试验数据进行辨识,能较为准确地获得全部气动参数,且结果具有唯一性。其中CD0的最大误差仅为0.43%,比极大似然法误差小了1个量级;与极大似然法误差最接近的是CMα0的2.8%,仍小于极大似然法。在极大似然法难以辨识的5个气动参数中,联合辨识方法所得结果的误差仍然较小,对于完全没有对应数据的Clp,辨识误差仍也仅有12.7%。以上结果表明联合辨识方法消除了气动参数辨识的局限性和差异性,且能减少测量噪声的影响。 2)联合辨识方法在部分试验数据缺失的条件下,通过主动利用气动辨识的矛盾性,能得到对应气动参数及试验数据辨识值。对于无法测量的攻角,其t0时刻的辨识值αt0和βt0误差大多在3%~8%,最大误差为10.4%,表明联合辨识方法具有实际工程意义。 3) 以数值仿真数据、风洞试验数据及现有方法辨识值作为先验知识,确定设计变量的基准值和设计空间,可以有效减少弹道计算的发散,提高优化效率,确保获得准确的优化结果。 对于导弹等包含三通道舵偏角导数的飞行器,过强的非线性运动、过多的气动参数和敏感的闭环控制系统都会增大联合辨识的难度,且该类飞行器通常可以有针对性地进行程控飞行,较少面临没有测量数据的情况。因此,联合辨识方法更适用于不包含舵面和闭环控制系统的无控段飞行,此类对象仅需替换相关的运动方程即可。2 现有多条试验数据辨识方法

3 联合辨识方法
3.1 参数辨识方法
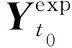
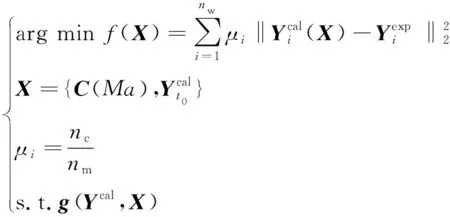
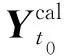
3.2 可行样本选取方法
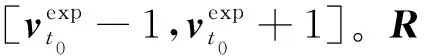

3.3 具体流程
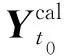
4 仿真验证
4.1 参数设置

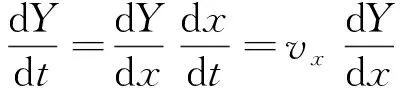
4.2 现有方法优化结果
4.3 联合辨识方法优化结果

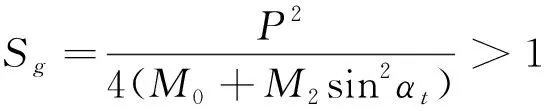

5 结 论

