三级供应链上企业低碳生产的演化博弈研究

张学军,梁亚娟

(河南科技大学 商学院,河南 洛阳 471023)

我国工业企业迅速发展,但经济发展引起的诸多环境问题引起学者们广泛关注[1]。根据国际能源署统计,截至2015年,中国的碳排放量已经远远超过其他国家,且制造企业成为碳排放的主要来源[2]。近年来,人们越来越注重环境的保护,低碳化产品的购买量也逐渐提高。因此,企业进行低碳化生产,不仅影响产品的市场需求,同时也影响着企业的收益。目前,企业的低碳生产主要由政府调控,但这种方法属于外部治理,通常达不到碳减排的要求,降低碳排放最根本的解决途径是供应链上的节点企业进行低碳生产,即供应链上负责提供原材料或半成品的供应商和主要负责进行产品加工生产的制造商[3]。同时,如果零售商分担供应商和制造商的减排成本,对企业的决策也具有重要影响。因此,研究供应链上的企业低碳生产行为,具有重要的意义。

一、文献综述

在此大背景下,企业的低碳生产问题吸引着越来越多的学者去探讨和研究。另外,一些学者从博弈论的角度对企业低碳生产行为展开研究。主要从以下几个方面进行。

(一)两主体博弈

在政府与企业的博弈中,Barcena-Ruiz通过建立企业和政府之间关于低碳技术水平和碳税税率的博弈模型来研究企业和政府之间的博弈关系[4];Wu等通过构建政府和企业之间关于低碳战略的演化博弈模型来评估企业低碳战略的扩散及应用[5];王文举和姚益家认为在碳税规制下,政府可以向企业征收一定的碳税来提高企业进行高碳排放生产的代价,从而促使企业进行低碳生产[6];而姚冠新等则认为企业想要进行低碳生产,仅靠企业自身的低碳生产意愿是不可行的,还需要政府的引导和支持,因此,地方政府为企业提供一定程度的减排补贴更有助于企业实现低碳化生产[7]。但大多数学者将政府惩罚与奖励同时纳入考虑,即政府根据企业选择的生产方式,将碳税政策和碳减排补贴政策结合考虑以制定最优的减排政策。如果企业选择进行低碳化生产,则政府应对企业提供补贴以作为奖励,如果企业选择传统发展模式,政府可对企业进行惩罚[8-10]。

在企业之间的博弈中,Meng等通过构建Stackelberg模型和Nash模型来研究在碳税规制下两个相互竞争的企业的策略选择行为,同时比较了两个博弈模型结果的区别[11];肖丁丁等为研究两类企业对不同创新模式的选择问题,构建了一个演化博弈模型,分析了在不同的碳税税率和交易价格下企业的动态演化过程[12]。

在两级供应链博弈中,Yang等为研究供应链上企业的利润分享原理和决策行为,构建了碳税背景下的供应商与制造商两级供应链博弈模型[13]。 Liu等通过构建供应链上的零售商和制造商之间的Stackelberg模型来研究消费者对企业碳排放的敏感程度会对供应链上企业的行为决策产生怎样的影响,同时分析了两个企业之间的互相竞争是否会影响企业之间利润分配的问题[14];姜跃等和李友东等通过构建博弈模型研究了两级供应链上零售商与制造商的减排成本如何进行分配的问题[15-16]。

(二)三主体博弈

徐建中等构建了装备制造企业、政府和第三方监管机构在低碳环境下的三方演化博弈模型,研究了三个主体在低碳生产过程中的行为决策和系统演化至稳定状态的影响因素[17];范如国等构建了中央政府、地方政府和企业的三主体博弈模型,分析了在低碳生产中三方之间的行为关系[18];陆菊春等构建了政府、建筑企业和消费者三主体的演化博弈模型,研究了建筑企业进行低碳生产的动态演化过程和行为策略选择[19];姜跃等构建了供应商、制造商以及零售商组成的三方博弈模型,分析了三级供应链上企业进行低碳生产的主体决策问题[20]。

综上所述,国内外大多数学者以两个博弈主体作为研究对象,很少将三个主体同时纳入研究范围,关于供应链上主体低碳生产行为的博弈研究文献更是不多,且主要以两级供应链为主,鲜有文献将供应链上的三个主体同时作为研究对象来研究三级供应链上的低碳生产博弈行为。基于此,本文在有限理性假设条件下,构建了由供应商、制造商和零售商组成的三级供应链的三方演化博弈模型,运用复制动态方程求解并分析了参数的变动对三个参与主体策略选择的影响,最后探究得出影响每个主体决策的因素。

二、基本假设与模型构建

(一)问题描述和基本假设

1.博弈主体。本文假设一个由供应商、制造商和零售商构成的三级供应链,且该供应链上的企业都是有限理性的。其中,供应商向制造商提供生产所需的原料或半成品,制造商负责将其加工生产成产成品并批发给零售商,最后由零售商将这些产品销售给消费者。随着低碳环保意识的不断加强,消费者更愿意购买低碳产品。因此,低碳产品市场需求的不断增加使得零售商愿意分担产品生产链上的减排成本。

本文研究还需要做一些基本假设:一是供应商和制造商生产的产品足够满足市场的需求,即不会出现产品短缺的问题;二是消费者也是有限理性的。

2.博弈主体行为策略。供应商的行为策略选择有进行低碳生产投入和不进行低碳生产投入两种,其策略集记为(X1,X2);制造商的行为策略选择也分进行低碳生产投入和不进行低碳生产投入,其策略集记为(Y1,Y2);零售商的行为策略选择有分摊供应商和制造商的减排投入成本和不分摊供应商和制造商的减排投入成本,其策略集记为(Z1,Z2)。

3.模型假设及相关参数设定。假设1:供应商和制造商都按传统的生产模式进行生产,即都不进行碳减排投入,零售商也不考虑承担减排生产的投入成本时,供应商、制造商和零售商的收益分别为M1,M2,M3,M1>0,M2>0,M3>0,供应商和制造商进行低碳生产的投入成本分别为C1,C2,C1>0,C2>0。零售商分担的减排投入成本为αC1+βC2,其中α(α>0),β(β>0)分别是零售商选择分担供应商和制造商进行低碳生产投入成本的比例。

假设2:只有供应商选择进行低碳生产投入,而制造商仍按原来的生产方式进行生产,则供应链上最终生产的产品为低碳产品,消费者愿意花更多的钱去购买。

若零售商不分担供应商的减排投入成本,供应商的收益为(1+λ1)M1-C1,其中λ1(λ1>0)表示供应商进行低碳生产投入使其收益增加的比率。而不进行低碳生产投入的制造商和零售商将也会共享收益,这就是“搭便车”行为,此时制造商将获得比传统生产时更多的收益,其收益为G1;零售商将获得的共享收益为H1。

若零售商分担供应商的减排投入成本,供应商的收益为(1+λ1)M1-(1-α)C1,此时不进行低碳生产投入的制造商获得的共享收益为G2,零售商的收益为H1-αC1。

假设3:只有制造商选择进行低碳生产投入,而供应商仍按原来的生产方式生产,则此供应链上最终生产的产品仍为低碳产品,消费者愿意花更多的钱去购买。

若零售商不分担制造商的减排投入成本,制造商的收益为(1+μ1)M2-C2,其中μ1(μ1>0)表示制造商进行低碳生产投入使其收益增加的比率。而不进行低碳生产投入的供应商和零售商也会存在“搭便车”行为,此时供应商的共享收益为I1;零售商的共享收益为H2。

若零售商分担制造商的减排投入成本,制造商的收益为(1+μ1)M2-(1-β)C2,此时不进行低碳生产投入的供应商获得的共享收益为I2,零售商的收益为H2-βC2。

假设4:供应商和制造商都进行低碳生产投入,则他们对整条供应链上的碳减排都有贡献,生产的产品也更低碳,此时供应链上的参与主体会获得更多的收益。

若零售商不分担供应商和制造商的减排投入成本,则供应商的收益为(1+λ2)M1-C1,其中λ2(λ2>0)表示供应商和制造商都进行低碳生产投入时使供应商收益增加的比率,且λ2>λ1;制造商的收益为(1+μ2)M2-C2,其中μ2(μ2>0)表示供应商和制造商都进行低碳生产投入时,使制造商收益增加的比率,且μ2>μ1。零售商也获得比原来更多的收益,其收益为H3。

若零售商分担供应商和制造商的减排投入成本,则供应商的收益为(1+λ2)M1-(1-α)C1,制造商的收益为(1+μ2)M2-(1-β)C2,此时零售商的收益为H3-(αC1+βC2)。

相关参数设定及含义由表1所示。

表1 主要参数设定及含义

续表1

(二)模型的建立

基于以上模型的假设和参数的设定,可以构建供应链上供应商、制造商和零售商三个博弈主体之间的7种博弈组合(当供应商和制造商都不进行低碳生产投入时,零售商没有分担低碳生产投入成本的必要,即零售商都会选择不分担低碳生产投入成本)及不同组合模式下的收益矩阵,具体如表2所示。

表2 供应链上供应商、制造商和零售商的策略组合和支付矩阵

三、演化博弈模型分析

(一)三方演化博弈的复制动态分析

假设供应商企业进行低碳生产投入的比例为x(0≤x≤1),则不进行低碳投入的比例为1-x;制造商企业进行低碳生产投入的比例为y(0≤y≤1),不进行低碳投入的比例为1-y;零售商企业选择分摊供应商和制造商的减排投入的比例为z(0≤z≤1),选择不分摊的比例为1-z。

供应商企业选择进行低碳生产投入的期望收益为:

Ux1=yz[(1+λ2)M1-(1-α)C1]+

y(1-z)[(1+λ2)M1-C1]+

(1-y)z[(1+λ1)M1-(1-α)C1]+

(1-y)(1-z)[(1+λ1)M1-C1]

供应商企业选择不进行低碳生产投入的期望收益为:

Ux2=yzI2+y(1-z)I1+(1-y)(1-z)M1

供应商企业的平均期望收益为:

U1=xUx1+(1-x)Ux2

构造供应商企业行为策略的复制动态方程为:

=x(1-x)(Ux1-Ux2)

+zM1+zαC1-C1+λ1M1]

同理,制造商企业选择进行低碳生产投入的期望收益为:

Uy1=xz[(1+μ2)M2-(1-β)C2]

+x(1-z)[(1+μ2)M2-C2]

+(1-x)z[(1+μ1)M2-(1-β)C2]

+(1-x)(1-z)[(1+μ1)M2-C2]

制造商企业选择不进行低碳生产投入的期望收益为:

Uy2=xzG2+x(1-z)G1+(1-x)(1-z)M2

制造商企业的平均期望收益为:

U2=yUy1+(1-y)Uy2

构造供应商企业行为策略的复制动态方程为:

=y(1-y)(Uy1-Uy2)

+z(βC2+M2)-C2+μ1M2]

零售商企业选择分摊供应商和制造商的减排投入的期望收益为:

Uz1=xy[H3-(αC1+βC2)]

+x(1-y)(H1-αC1)

+(1-x)y(H2-βC2)

零售商企业选择不分摊供应商和制造商的减排投入的期望收益为:

Uz2=xyH3+x(1-y)H1

+(1-x)yH2+(1-x)(1-y)M3

零售商企业的平均期望收益为:

U3=zUz1+(1-z)Uz2

构造零售商企业行为策略的复制动态方程为:

(UZ1-UZ2)=z(1-z)[x(M3-αC1)

+y(M3-βC2)-xyM3-M3]

联立复制动态方程F(x)、F(y)和F(z),则组成了供应商、制造商和零售商动态演化的三维动力系统。当供应商、制造商和零售商不同策略的期望值一致时,系统能够维持在均衡状态,可解得:

x*=[C2-μ1M2-z(βC2+M2)]/[M2+μ2M2-μ1M2-G1+z(G1-G2-M2)]

y*=[C1-λ1M1-z(M1+αC1)]/[M1+λ2M1-λ1M1-I1+z(I1-I2-M1)]

z*=[C2-μ1M2-x(M2+μ2M2-μ1M2-G1)]/[βC2+M2+x(G1-G2-M2)]

即供应商企业以 x*=[C2-μ1M2-z(βC2+M2)]/[M2+μ2M2-μ1M2-G1+z(G1-G2-M2)] 的概率选择进行低碳生产投入,从x*式中可看出供应商企业是否进行低碳生产取决于制造商进行低碳生产时的投入成本、制造商进行低碳生产投入使其收益增加的比率、供应商和制造商都进行低碳生产时,使制造商收益增加的比率、制造商按传统方式生产时取得的收益、零售商选择分担制造商进行低碳生产投入成本的比例、只有供应商选择进行低碳生产且零售商不分担供应商的减排投入成本时,制造商的共享收益、只有供应商选择进行低碳生产且零售商分担供应商的减排投入成本时,制造商的共享收益和零售商企业选择分摊供应商和制造商的减排投入的概率;制造商企业以 y*=[C1-λ1M1-z(M1+αC1)]/[M1+λ2M1-λ1M1-I1+z(I1-I2-M1)]的概率选择进行低碳生产投入,从y*式中可看出制造商企业是否进行低碳生产取决于供应商进行低碳生产时的投入成本、只有供应商进行低碳生产投入使其收益增加的比率、供应商按传统方式生产时取得的收益、零售商选择分担供应商进行低碳生产投入成本的比例、供应商和制造商都进行低碳生产时,使供应商收益增加的比率、只有制造商选择进行低碳生产且零售商不分担制造商的减排投入成本时,供应商的共享收益、只有制造商选择进行低碳生产且零售商分担制造商的减排投入成本时,供应商的共享收益及零售商企业选择分摊供应商和制造商的减排投入的概率;零售商企业以 z*=[C2-μ1M2-x(M2+μ2M2-μ1M2-G1)]/

[βC2+M2+x(G1-G2-M2)] 的概率选择分摊供应商和制造商的减排投入,从z*式中可看出零售商企业是否选择分摊供应商和制造商的减排投入与制造商进行低碳生产时的投入成本、制造商进行低碳生产投入使其收益增加的比率、供应商和制造商都进行低碳生产时,使制造商收益增加的比率、制造商按传统方式生产时取得的收益、零售商选择分担制造商进行低碳生产投入成本的比例、只有供应商选择进行低碳生产且零售商不分担供应商的减排投入成本时,制造商的共享收益、只有供应商选择进行低碳生产且零售商分担供应商的减排投入成本时,制造商的共享收益以及供应商企业进行低碳生产投入的比例有关。

(二)三方演化博弈的均衡点稳定性分析

为找寻各博弈方均达到稳定状态时的博弈均衡点,令F(x)=0, F(y)=0 ,F(z)=0,则可得到该动力系统的9个均衡点,分别为A1(0,0,0)、A2(1,0,0)、A3(0,1,0)、A4(0,0,1)、A5(1,1,0)、A6(1,0,1)、A7(0,1,1)、A8(1,1,1)和A9(x*,y*,z*),

其中,A9(x*,y*,z*)是复制动态方程F(x)、F(y)和F(z)联立方程组的解,A1～A8构成了该演化博弈的边界,由此边界围成的区域C就是该三方演化博弈的均衡解域,即 C={(x,y,z)|0≤x≤1,0≤y≤1,0≤z≤1} 。对于A1～A8渐进稳定性的分析可以通过该系统的雅克比矩阵的局部稳定性得到。

首先,分析均衡点A1(0,0,0),此时的雅克比矩阵为:

根据李雅普诺夫第一方法(间接法)可知,当所得雅克比矩阵对应的特征值均为负时,该均衡点为稳定点。在对角矩阵中,矩阵的特征值为主对角线上的元素,因此,在式J1中,当 λ1M1-C1,μ1M2-C2,-M3均为负数时,均衡点A1(0,0,0)是一个稳定点,即为演化稳定策略;当λ1M1-C1,μ1M2-C2,-M3均为正数时,均衡点A1(0,0,0)为不稳定点;当λ1M1-C1,μ1M2-C2,-M3中有一个或两个为正数时,均衡点A1(0,0,0)为鞍点。显然, -M3<0为一个确定的负数,所以A1(0,0,0)可能为稳定点也可能为鞍点。

当均衡点为A2(1,0,0)时,雅克比矩阵为:

在式J2中,-αC1<0为负数,则均衡点A2(1,0,0)为鞍点或稳定点。

同理,可通过分析其他各个均衡点特征值的正负,来分析该均衡点的稳定性,其各均衡点对应的特征值情况如下表3所示。

表3 各均衡点特征值的情况

由表3可看出A1～A8的特征值3都为负值,则A1～A8均可能为稳定点或鞍点。

(三)演化结果分析

由以上分析可看出,当λ1、λ2、μ1、μ2、α和β所在区间发生变化时,演化稳定策略也将发生改变。

情况一当零售商企业选择不分摊供应商和制造商的减排投入成本时

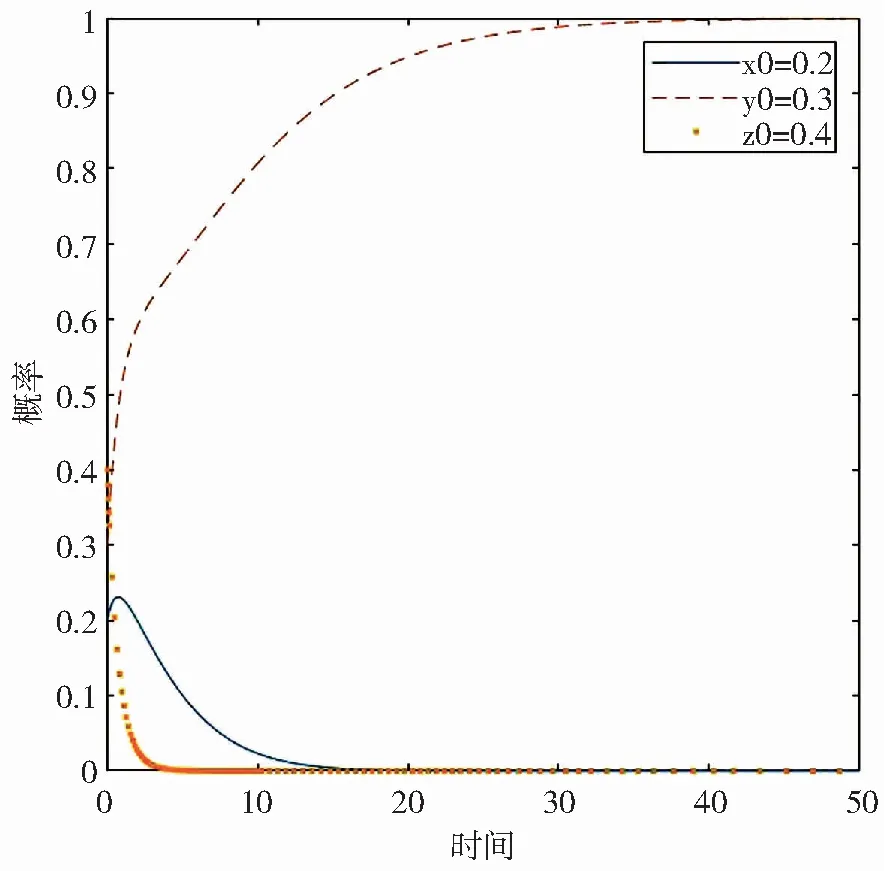
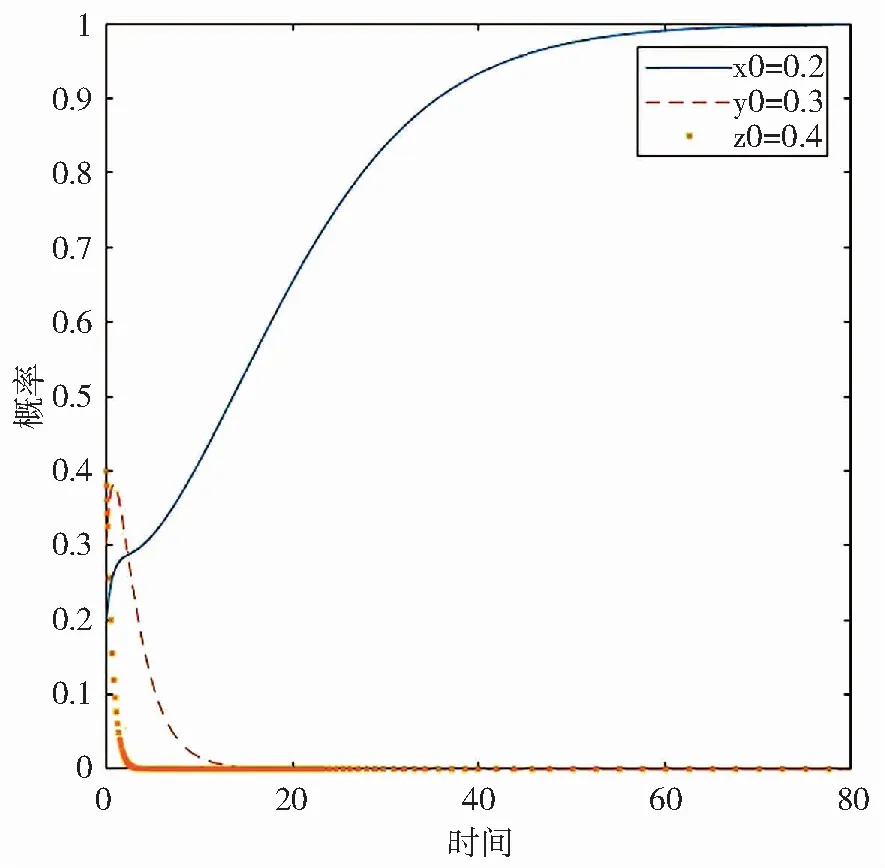
(1)当0<λ1

当供应商和制造商进行低碳生产收益增加的比率λ1、λ2、μ1和μ2都比较小,即0<λ1

(2)当0<λ1

当供应链上的制造商进行低碳生产收益增加的比率μ1和μ2满足C2/M2<μ1<μ2<(C2+G1-M2)/M2时,制造商进行低碳生产使其增加的收益大于他为此而投入的成本,但小于他“搭便车”行为获得的共享收益。若此时供应商进行低碳生产收益增加的比率λ1和λ2仍然为0<λ1

(3)当C1/M1<λ1<λ2<(C1+I1-M1)/M1且0<μ1

当供应链上的供应商进行低碳生产收益增加的比率λ1和λ2满足C1/M1<λ1<λ2<(C1+I1-M1)/M1时,供应商进行低碳生产使其增加的收益大于他为此而投入的成本,但小于他“搭便车”行为获得的共享收益。若此时制造商进行低碳生产收益增加的比率μ1和μ2仍然为0<μ1

(4)当C1/M1<λ1<λ2<(C1+I1-M1)/M1且C2/M2<μ1<μ2<(C2+G1-M2)/M2时,三维动力系统的演化稳定策略(ESS)为A2(1,0,0)或A3(0,1,0)。

当供应链上的供应商和制造商进行低碳生产收益增加的比率λ1、λ2、μ1和μ2满足C1/M1<λ1<λ2<(C1+I1-M1)/M1和C2/M2<μ1<μ2<(C2+G1-M2)/M2时,供应商和制造商进行低碳生产使其增加的收益大于他们为此而投入的成本,但小于他们“搭便车”行为获得的共享收益。此时,A2(1,0,0)或A3(0,1,0)是系统的稳定点,即供应商进行低碳生产投入,制造商不进行低碳生产投入或供应商不进行低碳生产投入,制造商进行低碳生产投入。但具体会沿着哪条路径收敛于哪个均衡点,与支付矩阵和系统的初始状态都有关。

(5)当(C1+I1-M1)/M1<λ1<λ2且(C2+G1-M2)/M2<μ1<μ2时,三维动力系统的演化稳定策略(ESS)为A5(1,1,0)。

当供应链上的供应商和制造商进行低碳生产收益增加的比率λ1、λ2、μ1和μ2满足(C1+I1-M1)/M1<λ1<λ2且(C2+G1-M2)/M2<μ1<μ2时,供应商和制造商都进行低碳生产投入所获得的收益分别大于他们从对方进行低碳生产投入但自己采取“搭便车”行为所获得的共享收益I1和G1。此时A5(1,1,0)是系统的稳定点,即供应商和制造商都进行低碳生产投入。

情况二当零售商企业选择分摊供应商和制造商的减排投入成本时

(1)当0<λ1<(C1-αC1)/M1、λ1<λ2<(I2+(1-α)C1-M1)/M1且 0<μ1<(C2-βC2)/M2、μ1<μ2<(C2-βC2+G2-M2)/M2,同时0<α

当供应商和制造商进行低碳生产收益增加的比率λ1、λ2、μ1和μ2以及零售商选择分担供应商和制造商进行低碳生产投入成本的比例α和β满足0<λ1<(C1-αC1)/M1、λ1<λ2<(I2+(1-α)C1-M1)/M1且0<μ1<(C2-βC2)/M2、μ1<μ2<(C2-βC2+G2-M2)/M2,同时0<α

(2)当(C1-αC1)/M1<λ1<λ2<(I2+(1-α)C1-M1)/M1且0<μ1<(C2-βC2)/M2、μ1<μ2<(C2-βC2+G2-M2)/M2,同时0<α

当供应商进行低碳生产收益增加的比率λ1和λ2以及零售商选择分担供应商和制造商进行低碳生产投入成本的比例α和β满足(C1-αC1)/M1<λ1<λ2<(I2+(1-α)C1-M1)/M1同时0<α

对于其他均衡点的稳定性分析与上面分析方法同理,这里不做过多论述。

四、数值仿真分析

本文在理论分析的基础上,运用Matlab软件对模型进行数值仿真验证,设x0、y0和z0分别表示供应商选择“低碳生产”、制造商选择“低碳生产”和零售商愿意“分担减排”成本。初始时间为0,结束时间为100,初始状态为(x0,y0,z0)=(0.2,0.3,0.4)。并假设初始参数值分别为:M1=3,M2=5,M3=4,C1=8,C2=1.5,I1=3.5,I2=3.7,G1=5.52,G2=5.72,H1=4.5,H2=4.7,H3=5.1。在情况一中,当零售商企业选择不分摊供应商和制造商的减排投入时,α=0,β=0。

(1)当λ1=0.25、λ2=0.3、μ1=0.2、μ2=0.35,即当满足0<λ1

图1 均衡策略A1的动态演化仿真图

(2)其他参数值不变,当μ1、μ2变为μ1=0.33、μ1=0.37,即当满足0<λ1

图2 均衡策略A3的动态演化仿真图

(3)其他参数值不变,当λ1、λ2变为λ1=0.3、λ1=0.37,即当满足C1/M1<λ1<λ2<(C1+I1-M1)/M1且0<μ1

图3 均衡策略A2的动态演化仿真图

其他均衡点的仿真验证与上面实验做法相同,这里不再赘述。

五、结论与建议

本文在有限理性的假设前提下,建立了三级供应链上供应商、制造商和零售商三主体演化博弈模型,构造复制动态方程并求解得到该动力系统的9个均衡点,分析了均衡点的稳定性,研究了供应链上供应商、制造商和零售商三个主体在不同情况下的行为策略选择。通过分析得出以下结论:第一,供应商和制造商的行为策略选择不仅与进行低碳生产收益增加的比率有关,还与他们采取“搭便车”行为获得的收益高低以及零售商分担的低碳生产投入成本的比例都有关。第二,供应链上的供应商和制造商都选择进行低碳生产,同时零售商愿意分担供应商和制造商的低碳生产投入成本时,达到该模型的最优稳定策略A8(1,1,1),供应链上生产的最终产品更环保,同时供应商、制造商和零售商将获得更高的利润。

为了使该模型更加接近于最优的稳定策略A8(1,1,1),同时使供应链上的产品生产向着更环保的方向发展,结合以上分析,给出以下几点建议。

第一,为保证零售商选择分摊低碳生产投入成本,三级供应链上的供应商、制造商和零售商之间应签订减排成本分摊契约,这样提高了供应链上最终产品的低碳化水平,同时整个供应链上的参与主体将获得更高的收益。

第二,为激励供应链上的企业进行低碳生产,政府调控方面也应发挥作用。政府应加大对进行低碳生产企业的补贴力度,从而提高低碳产品的市场竞争力;帮助企业引进低碳生产设备,支持企业进行低碳生产的研发和创新,这对供应链上的企业向着低碳化生产具有很大的推动力。同时,应适当惩罚按传统方式进行生产的企业,如政府可制定相关的碳税政策向该类企业征收碳税,从而促使企业进行低碳生产。

第三,从消费者角度来说,应通过各种渠道来加大绿色低碳宣传力度,提高消费者的环保素养,增强消费者的环保意识,让更多的消费者具有低碳绿色偏好,更愿意选择购买低碳化产品,从而激发供应链企业生产低碳化产品的潜能[21]。

第四,根据消费者越来越倾向于购买低碳化产品的行为,供应链上的企业在产品的定价方面,应对低碳化的产品制定更高的销售价格,这样整个供应链上将获得更高的利润,供应商、制造商和零售商的收益都会增加,从而提高产品的低碳化水平,促进我国低碳经济发展。