基于纵向阻抗的变压器虚拟相位保护

夏经德,苗思雨,邵文权,杨秀川,徐 彦

(西安工程大学 电子信息学院,陕西 西安 710048)

0 引 言

在电力系统中,变压器是电力系统的重要设备,保证其稳定运行将直接关系到整个电力系统的安全。在过去的几十年里,方向比较纵联保护得到了充分的改进和发展[1],并且已成为发电机、变压器以及输电线路最常采用的保护方式之一。现如今的变压器由于生产工艺的成熟,所以结构上比较可靠,基本不会有故障发生,但是在实际运行中仍然会遇到各种情况[2-5]。

近年来,人们进行了大量变压器保护相关工作的研究,尤其是传统的差动保护容易受到CT饱和及励磁涌流影响方面的研究有很大进展。文献[6]提出一种变压器保护算法。当区外故障时,纵向阻抗大于动作门槛;区内故障时,纵向阻抗小于动作门槛,但裕度偏小,而虚拟相位保护可以避免这个问题。文献[7]阐述了利用变压器二次侧故障前后的电压变化幅值构成判据,通过改进的邻近聚类法快速区分故障区段。文献[8]提出利用波形正弦度对励磁涌流进行识别,但是在带故障合闸时会有延时。文献[9]对励涌的二次谐波进行分析,拟合后得到二次谐波含量表达式,但未对三绕组变压器涌流的二次谐波含量进行分析。文献[10]从直流偏磁的磁通特性对变压器的几种饱和特征进行分析,解决了变压器三角形回路无法配置直流偏磁保护的问题。文献[11]阐述了基于小波变换的配电变压器差动保护相位补偿方法,该方法依据启动元件进行故障区域识别。文献[12]指出变压器传统差动保护在CT饱和时会误动作的原因。文献[13]阐述了利用回归算法进行变压器的故障检测并完成了仿真验证。文献[14]提出了一种利用区内故障电流和涌流波形的显著差异构造判据来识别励磁涌流。文献[15]对110 kV变压器的短路阻抗进行了优化调整。文献[16]利用等值阻抗法计算了220 kV降压变各侧近区或出口短路时的短路电流,为故障防范提供了数据支持。

本文研究220 kV系统中主变的主保护,介绍了三相双绕组变压器的保护方法,即在区内区外故障时以绕组之间虚拟点的纵向阻抗相位差为判据,能够有效避免发生励磁涌流和CT饱和对差动保护影响的问题。仿真验证了在区内故障和区外故障时,纵向阻抗虚拟相位会有一个以90°为界限的差异。同时在发生励磁涌流和CT饱和时,虚拟相位保护能不误动,具有较好的抗误差能力。

1 基于纵向阻抗双绕组变压器保护

由文献[17]知纵向阻抗的定义,结合双绕组变压器的特点来分析,如图1所示为双绕组变压器的等效网络。

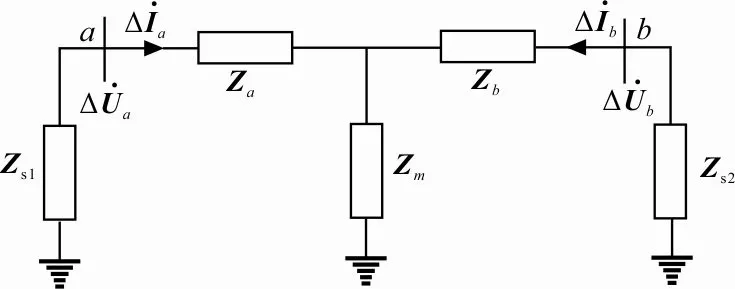
图1 220 kV系统变压器的等效网络

1.1 内部故障

图2为在双绕组变压器内部发生故障时的等效网络图。

图2 发生内部故障时变压器等效网络

(1)

接着对a侧和b侧的电压故障分量进行处理,图3所示为a-b侧各个故障电压的平移方向。

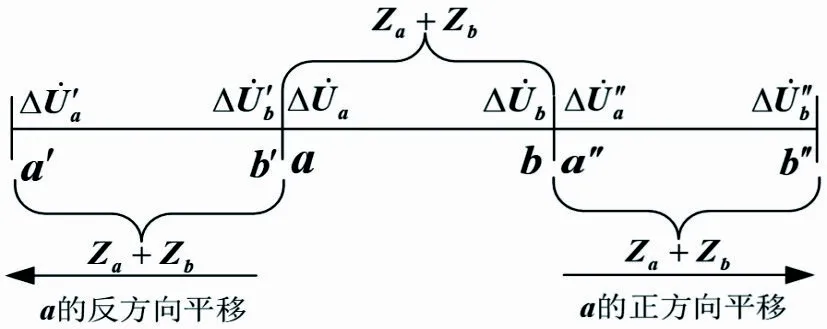
图3 a-b侧各故障电压的平移方向

(2)

(3)

(4)

显然,当内部发生故障时会有一个反向的虚拟相位差。

综上所述,在内部故障时,a侧和b侧的电压量朝着保护正、反方向分别平移一个(Za+Zb)电气距离之后的纵向阻抗的虚拟相位差达到180°。

1.2 外部故障

在发生区外故障时,由于风机出口的电压经过高频电力电子开关器件后会带来谐波,再加上区外故障时会有大量的谐波产生从而影响保护判别。变压器外部发生故障时的等效网络如图4所示。

图4 外部发生故障时等效网络

从图4可以看出,各个参数同内部故障等效图一致,并且根据图4可以通过基尔霍夫电流定律得到双绕组变压器电流关系符合式,即

(5)

(6)

(7)

(8)

由上述可知,虚拟相位保护在区外故障时分别向a侧保护的正反方向平移一个(Za+Zb)的电气距离时,即便有外界大量谐波的干扰,依然可以得到外部故障时纵向阻抗的虚拟相位差值趋近于0°。

2 CT饱和等情况下保护的动作情况

CT作为电力系统的重要测量元件,广泛应用于保护、测量、监控等各个领域[19]。由于电流中的非周期分量导致CT饱和,会造成保护误动或拒动[20],是因为随着电网的发展和电压等级不断增高,系统的短路容量不断增大,导致电网短路电流很大。当外部故障时流过各支路的电流差也可能很大,会造成某些支路的CT出现饱和,使保护装置误动作。保护用CT性能应满足在区外短路时,将电流互感器所在回路的一次电流传变到二次回路,且误差不超过规定值。避免引起差动保护的误动[21]。

2.1 CT饱和的波形及谐波的分析

电流互感器饱和时的波形如图5所示。图5中展示的波形为当CT发生饱和时,CT一、二次侧的电流波形的对比,饱和电流中暂态饱和占比30%,稳态饱和占比70%。

图5 CT饱和后一二次侧电流的波形

当CT出现饱和时,对二次侧的电流进行谐波分析,直流分量、基波、二次谐波、三次谐波、四次谐波、五次谐波、六次谐波和七次谐波的谐波含量分别为0.120、1.000、0.200、0.280、0.135、0.257、0.100和0.150。

当电流互感器发生暂态以及稳态饱和时,二次侧电流的谐波含量较大的有三次、五次、七次谐波,同时非周期分量和二次谐波也有一定比例。

2.2 CT饱和对保护判据的影响

设当a侧的CT发生深度饱和时,a侧的CT二次侧电流将下降至正常的50%,类似于分析区内外故障。此时由前述可知:

(9)

(10)

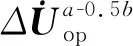
(11)

2.3 CT有10%误差的分析

现有用于保护的CT所允许的误差为10%,由前述的CT饱和达到最严重的50%可知,此时CT二次侧电流幅值衰减达到正常值的一半,保护依旧能可靠区分内部和外部故障。同理,10%的幅值衰减同样不会影响保护的可靠性。

sin(φx))dt=

(12)

sin(φx))dt=

(13)

式中:β为磁滞引起的相角差;φx为铁磁材料在线性传变区所需的时间而换算成的角度。在通过Ia和Ib的做比值之后的反正切得出饱和后的一次侧和二次侧电流和的相角差θ。

设φx=0.5°,β=8°,代入式(12)、(13)之后,再由上述处理方法可得θ为9.16°。

由上述可知,CT有10%误差的情况下,不论是相角还是幅值,均可以满足此方法的精度要求。保证了保护的可靠性。

综上所述分析可知,再发生CT饱和时,通过对得出的电压数据链进行分析,可以得出以下结论:

1) 发生CT饱和时,理论分析结果和区外故障时的电压数据链关系一致,也即最理想的情况下即CT没有传变误差时,其结果和区外发生故障时的结果一致;

2) 在最严重的情况下,即2个测量端任何一端达到饱和最严重的50%情况依然可靠不动作,故本保护有较好的抗CT的衰减能力,现有保护用的CT能够满足其对精度的要求。

3 励磁涌流的影响

判断变压器内部故障的主要方法是纵差保护,但发生励磁涌流时,保护常常会误动,因此鉴别励磁涌流是变压器保护研究的重要课题。现有的判别方法:利用10个半周波内三相差动电流第5级系数能量和进行判断[22];将电流进行广义S变换,结合幅值和频率信息熵2个指标进行判断[23];利用励磁涌流和短路电流的二阶泰勒展开系数进行判别[24]等。

励涌判别常采用的方法有二次谐波判据和间断角判据[25],但由于变压器制造工艺和材料会对二次谐波的产生带来影响,且采样信号多为高频信号,影响间断角的判别。当发生励磁涌流时,会含有数值很大的二次和三次谐波的分量,会使涌流呈现尖顶波的形状。

本文所研究的对象是220 kV电压等级下的三相双绕组变压器。例如在变压器一、二次侧的断路器都断开之后,在二次侧的断路器处于断开的状态下,将一次侧的断路器合上,此时将会出现幅值为4～8倍额定电流的的励磁涌流。文中用PSCAD搭建的模型进行涌流仿真。在仿真时,将剩磁设为一个固定值之后,改变合闸时间来模拟不同的合闸角对励磁涌流的影响。

在合闸角α为不同值时,得到的励磁涌流有不同的谐波含量。通过快速傅里叶变换后可以得出A、B、C三相各相的谐波分量,分别如表1所示。

表1 不同的合闸角时三相励磁涌流谐波含量结果

从表1可以看出,在α=0°时的励磁涌流的谐波含量主要为直流分量和二次谐波以及三次谐波,其余高次谐波占比很少。α=90°时,励磁涌流只有一些直流分量,二次谐波含量在1%左右,说明此刻几乎没有发生励磁涌流。α=180°的情况和α=0°的时候基本一致,都是有很大的直流分量以及二、三次谐波。

综合上述可知,取α=0°时刻来进行理论验证,当a侧空载合闸时,变压器b侧都是开路状态,故变压器b侧的串联阻抗Zb趋于无穷大。此时根据基尔霍夫电流定律可知:

(14)

如前述,在电压平移过后求得a-b侧的相角差为

(15)

由上述分析可知,通过对励磁涌流的特点进行分析可得:当发生涌流时,纵向阻抗虚拟相位保护的结果符合区外故障的特征。且在最恶劣的情况下(α=0°时空投),纵向阻抗虚拟相位保护的结果仍然趋于0°,保护不会动作。

综上所述,需要有一个稳定可靠的式子来判别区内、外故障,故结合前文理论分析,可以构造出式(16)作为判据:

(16)

根据式(16)所展示的判别式可知:当区内发生故障时,需满足判别式中的两式同时成立才能完成保护动作。在满足电流突变幅值大于整定值且2个测量端所得到的虚拟阻抗相位差大于90°时保护才会动作。式中x代表A、B、C三相中的任意一相。

4 仿真验证

4.1 仿真系统及其参数

本次仿真的平台是PSCAD电磁暂态仿真软件来进行仿真,采用的CT与传统差动保护所选取的一致;所选取的变压器为220 kV的三相双绕组有载调压变压器,其容量为100 MVA,可由变压器的铭牌上得到其一次侧额定电压为230(1±8×1.25%) kV,二次侧额定电压为35 kV;一次侧额定电流为251 A,二次侧额定电流为1 649.6 A;短路阻抗百分数为0.129 6。

利用PSCAD仿真软件构建了如图6所示的220 kV主变的拓扑结构,利用此拓扑结构来搭建220 kV系统的三相双绕组变压器的物理模型。

图6 220 kV主变压器拓扑结构

图6中有4个故障点,k2、k3为区内故障,k1、k4为区外故障,CT 1、CT 2分别为a侧和b侧的电流互感器;S1、S2为两侧的等效电源。其余电气量与前述一致。

4.2 仿真结果与分析

当在图6的k3点发生区内短路故障时,主要有单相,两相短路故障。根据前述的计算方法,可以得出变压器内部发生故障时的虚拟相位差的仿真结果,表2为发生区内故障时a-b两侧的纵向阻抗虚拟相位差,表中√表示动作,×表示不动作(后文同理)。

表2 发生区内故障时仿真结果

从表2可以看出,在变压器区内发生故障前后,无论是否有Rf的存在,故障相两侧纵向阻抗虚拟相位差均有明显的差异。故由此可以分析并得出结论:在变压器区内发生故障时,无论是否有过渡电阻Rf存在,保护并不会受影响,均仅会在故障相正确动作。

下面讨论在区外,即图6的k4点发生短路故障时,纵向阻抗虚拟相位保护和区内故障时的区别。表3所示为发生区外故障时的虚拟相位差。

表3 发生区外故障时仿真结果

从表3可以看出,当变压器发生区外故障时,虚拟相角差会有小的波动,但不超过5°,远小于保护的整定值|φset.x|=90°,由此我们可以得出结论:当区外发生故障时,无论Rf是否存在,保护均能正确反映故障位置,并可靠不动作。

为了验证在变压器发生励磁涌流以及CT饱和时的纵向阻抗虚拟相角差是否和前文所述一致,遂进行仿真验证,仿真结果如表4所示。

表4 发生励磁涌流和CT饱和时的仿真结果

从表4可以得出,发生励磁涌流以及CT饱和2种干扰因素情况下的仿真结果。首先分析在CT达到饱和时,即便是二次侧电流能衰减到原有的50%时,发生饱和的前后会有一些相角差的变化;而当变压器空投合闸时,产生的励磁涌流产生的影响也会使虚拟相位差有一定的波动。

综上所述,虽然励磁涌流和CT饱和能够对虚拟相位差产生一定影响,引起虚拟相位差的波动,但远达不到保护要动作的条件。所以此方法不会受到励磁涌流和CT饱和的干扰从而使保护误动作。

4.3 可靠性分析

保护的可靠性用可靠度Krely来表示,它是指在发生区外故障、CT饱和以及励磁涌流时,保护能够正确反映并且可靠不动作的能力,可靠度Krely的计算方法为保护的整定值与非故障时保护所测量到的值的比。采用差动保护和虚拟相位保护2种保护方式进行比较,表5展示了发生区外故障时的保护可靠性比较,表6为励磁涌流和CT饱和时保护可靠性的比较。

表5 区外故障时保护Krely的比较

表6 励磁涌流和CT饱和时保护Krely的比较

由表5、6可以得出:在有外部故障发生、产生励磁涌流及CT饱和时,虚拟相位保护的可靠度均比传统差动保护要高出数倍乃至数十倍之多,验证了在发生上述影响因素的情况下,虚拟相位保护可靠性高于传统差动保护。

5 结 语

文中提出了一种变压器纵向阻抗虚拟相位保护方法,经过理论分析和仿真验证之后,得出以下结论。当发生内部故障时,不管是何种故障,都会使变压器绕组间的纵向阻抗虚拟相位差为180°,在受到外部故障以及变压器励磁涌流或CT饱和(在最理想和最恶劣的情况)的影响时,都不会超过动作门槛值90°使保护误动作。此种保护算法结构简单,灵敏度好,易于整定,能较好地抵御CT的衰减且现有的CT精度可以满足文中的保护方法,抗过渡电阻能力较强,能够有效地抵御励磁涌流,以及一系列外部因素的影响,能够适应各种复杂的环境,具有一定的工程实用价值。