线性回归模型多变点的LAD-LASSO估计

王 珊,赵文芝

(西安工程大学 理学院,陕西 西安 710048)

0 引 言

变点是质量控制、信号处理、地震预测和神经医学等各个领域的普遍现象。统计学文献中包含大量与结构变化有关的变点问题,其中大部分是为单一变化而设计的[1-3]。然而,许多真实数据却很少出现单一变点,比如经济、金融和生物学数据通常会发生多次变化[4-6]。线性回归模型是统计数据分析的重要模型之一,在实际问题中应用广泛[7],因此,研究存在多个变点的线性回归模型具有现实意义[8-9]。

回归模型的随机误差项有时会呈现尖峰厚尾的统计特征,在能源期货波动率[10]、细菌繁殖[11]及浮游植物的运动模式[12]等许多自然现象中,厚尾分布已引起人们的广泛关注。LAD准则只考虑偏离的一次方,受异常值影响较小[13-14],因此更适合处理厚尾数据。大数据时代,高维复杂情形往往蕴含在实际问题中,例如风电预测、视频图像处理等。对高维数据特征进行筛选、剔除冗余特征是解决维数灾难问题的主要途径[15]。LASSO[16-17]是一种新的数据降维方法,它保持了子集收缩和岭回归的良好特征,从而能在参数估计的同时实现变量选择[18]。HARCHAOUI等提出了基于LASSO的多变点估计方法[19];LI等用自适应LAD-LASSO方法研究均值多变点估计问题[20]。不过,现有文献对多变点估计问题的研究方法存在所适用的模型不具备普适性或者缺乏稳健性等不足之处,如何克服这些缺点是值得考虑的问题。

本文将LAD-LASSO方法应用到一般的线性回归模型多变点估计问题中。该方法能同时对回归系数、变点的个数及位置进行估计,且对于厚尾数据具有良好的稳健性。采用Hausdoff距离度量变点估计值集合与变点真实值集合之间的距离,以此评价多变点估计的效果。最后用该方法估计上海机场股票收益率数据的方差变点,进一步验证LAD-LASSO方法对实际问题的可行性。

1 多变点线性回归模型

考虑多变点线性回归模型[18]

(1)

其中

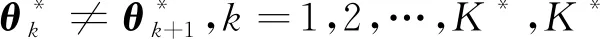
目标是通过已知的n对观测数据(xt,Yt),t=1,2,…,n估计模型(1)中的系数列向量βt,t=1,2,…,n,以及真实变点位置T*、变点个数K*。

2 LAD-LASSO估计

2.1 模型的转化

令Y=(Y1,Y2,…,Yn)T,E=(ε1,ε2,…,εn)T, 并且

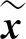
定义[18]

(2)

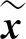
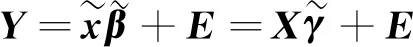
(3)

2.2 LAD-LASSO估计

问题(1)可表示为如下优化问题:

(4)

其中I{·}是示性函数。当βt+1=βt时,其值为0;反之其值为1。

使用文献[20]中的方法将式(4)中的约束条件进行放松:

(5)

式中:‖·‖1表示l1范数;

通过式(3)将问题(5)重新表示为

(6)

这等价于求解优化问题

(7)

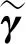
(8)

这样一来,问题(1)转化成了LAD-LASSO变量选择问题,其中λ是调节参数。λ的选取采用BIC方法[20](式中简记为BBIC),即

BBIC=nln(RSA/n)+dfln(n)/2

(9)

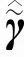
其中ej为第j个分量为1,其余分量为0的pn×1维列向量。这样,式(8)可以重新表示为

(10)

(11)

2.3 方差多变点估计

考虑方差多变点模型[21]

Yt=σtet,t=1,2,…,n

(12)

式中:σt为与时间有关的常数;{et,t=1,2,…,n}是i.i.d.随机变量序列,均值为0,方差为σ2。

式(12)右端可写成σt+σt(et-1)。令

σt=βt,σt(et-1)=εt,xt=1,

式(12)可转化为

Yt=βtxt+εt,t=1,2,…,n

(13)

即将模型(12)转化为多变点线性回归模型,进而可采用LAD-LASSO方法进行变点估计。

2.4 多变点估计结果的评价

对于多变点估计问题,本文用Hausdorff距离dH[22]评价多变点估计的效果。定义A,B分别代表变点估计值集合以及变点真实值集合,‖·‖表示欧式范数,则

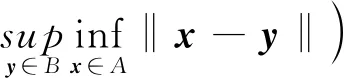
(14)

Hausdorff距离dH越小,多变点估计效果越好[23]。

3 随机模拟与实例分析

3.1 随机模拟

用随机模拟方法验证LAD-LASSO估计方法的有效性,并与传统的LASSO方法相对比。

数据生成过程如下:

Yt=βtxt+εt,t=1,2,…,n

(15)

其中,

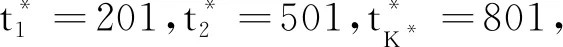
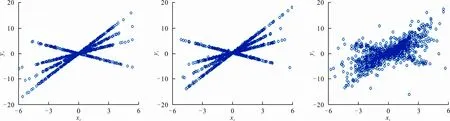
(a) 正态噪声下的观测样本 (b) 指数噪声下的观测样本 (c) t分布噪声下的观测样本

由图1(a)、(b)可知,当噪声服从正态分布和轻尾分布,即指数分布时,变点的发生用肉眼还可分辨;但在噪声服从厚尾分布,即t分布时,图1(c)中的变点用肉眼已经很难分辨,因此需要通过统计方法进行多变点估计。

用LAD-LASSO方法对以上生成的模拟数据进行多变点估计,并与传统的LASSO方法比较,变点估计结果见表1。

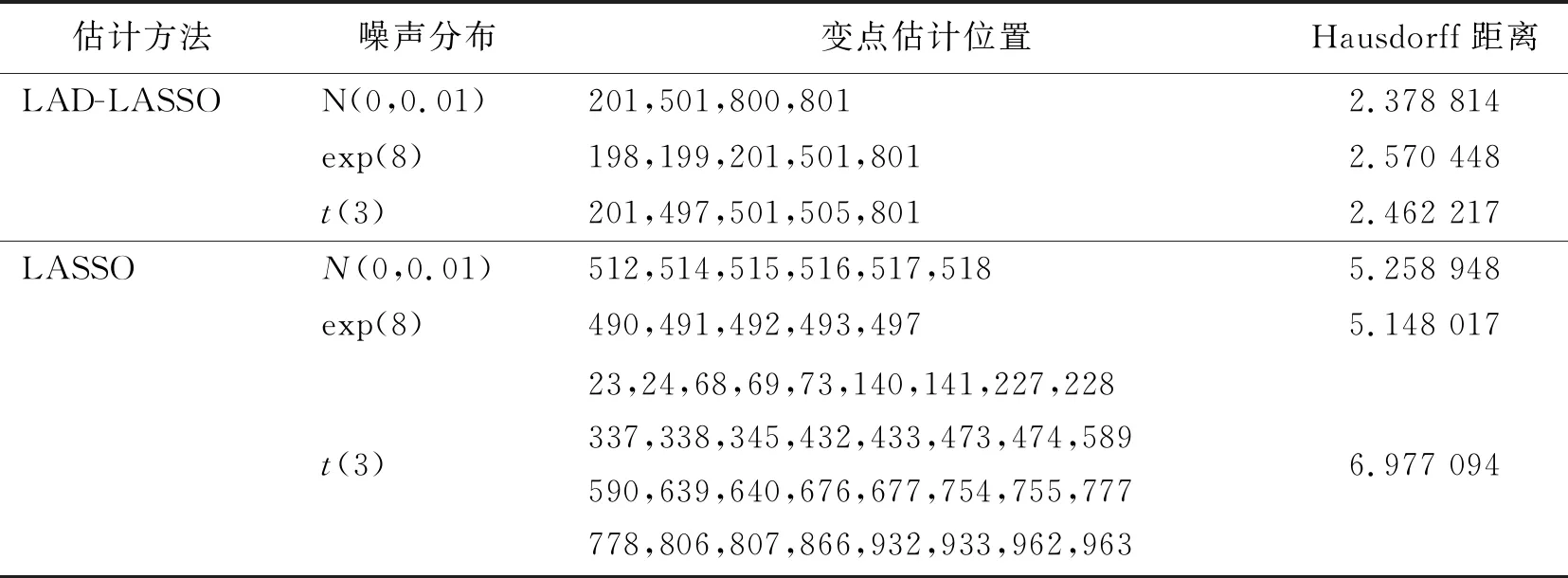
表1 不同分布下的LAD-LASSO估计及LASSO估计

由表1可知:LAD-LASSO的Hausdorff距离均小于LASSO的Hausdorff距离; 无论噪声服从轻尾还是厚尾分布,LAD-LASSO方法均优于LASSO方法。特别地,从变点估计的位置和数量上来看,当噪声服从厚尾分布,即t(3)分布时,LAD-LASSO方法的优势更加突出。

进一步直观地用散点图将LAD-LASSO变点估计与LASSO变点估计相对比,结果如图2所示。图2(a)、(b)、(c)是LAD-LASSO方法在3种噪声下的估计,(d)、(e)、(f)是LASSO方法进行变点估计的结果。可见,LAD-LASSO方法能比较准确地估计出真实变点位置,而LASSO方法无法估计出真实变点位置,而且估计结果不够准确。

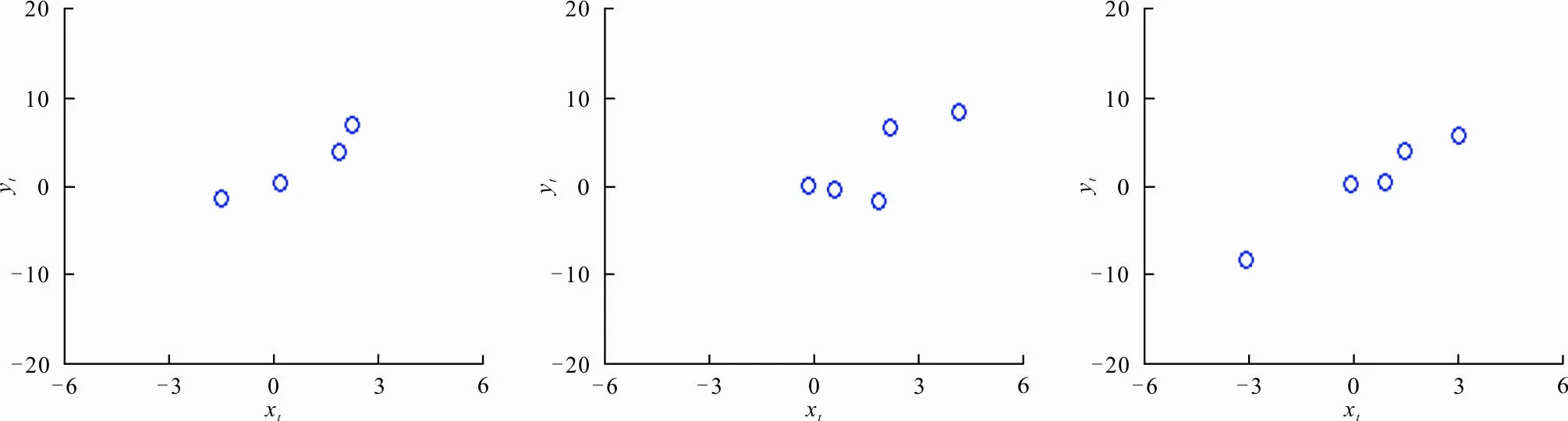
(a) 正态噪声下LAD-LASSO估计 (b) 指数噪声下LAD-LASSO估计 (c) t分布噪声下LAD-LASSO估计

3.2 实例分析

选取2013年1月到2017年3月上海机场股票(600009)收益率数据(数据来源:http://quotes.money.163.com/trade/lsjysj_600009.html)进行LAD-LASSO方差变点估计,验证该方法的有效性,结果如图3所示。

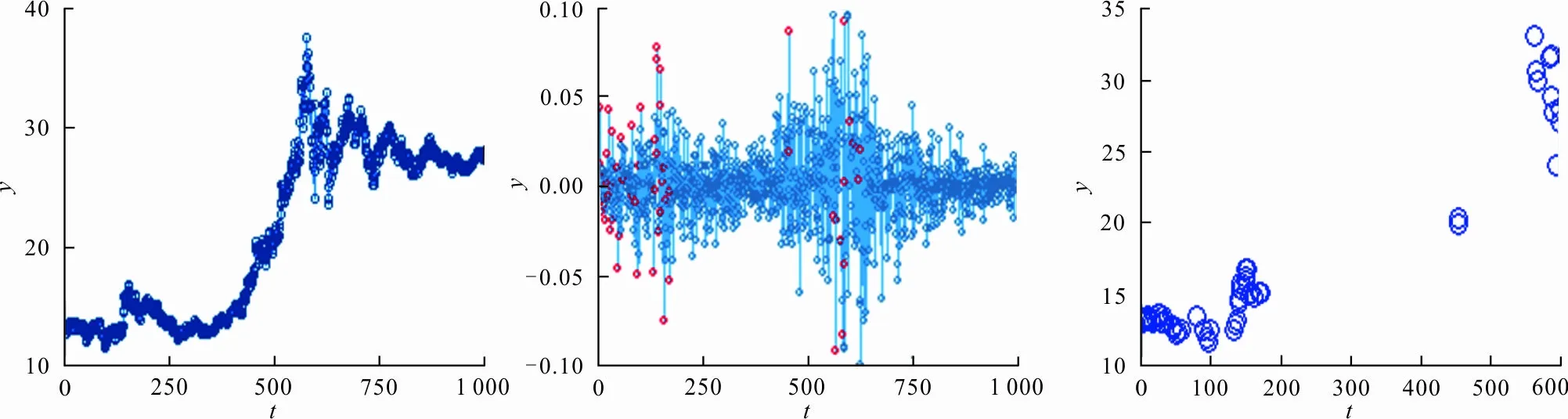
(a) 收盘价时序图 (b) 收益率时序图 (c) LAD-LASSO变点估计

由图3(c)可知,上海机场股票的收益率数据共有5次聚集性波动,认为该数据变点个数为5,变点估计结果见表2。2013年公司整体运营平稳,处于低速增长期;2014年是全面贯彻落实十八届三中全会精神的开局之年,机场运行业务量实现稳步增长;2015年民航业保持较快发展速度,上海机场出现了强劲的客流量增长,这是由于我国“十三五”规划对民航经济带来的积极影响。

表2 收益率数据变点估计结果

4 结 语

本文研究了线性回归模型多变点的LAD-LASSO估计方法。随机模拟结果表明:在序列误差服从不同分布的情况下,LAD-LASSO方法得到的Hausdorff距离小于LASSO方法得到的Hausdorff距离;在序列带t分布噪声影响下, LAD-LASSO估计结果表现更佳,该方法估计的变点位置在准确度上优于LASSO,而且对于厚尾数据能较好地估计变点位置,具有良好的稳健性。均值多变点、方差多变点模型均可作为线性回归模型的特例使用LAD-LASSO方法进行变点估计。实例分析结果表明,LAD-LASSO方法可用于处理实际问题。