企业研发投入对技术创新效率的影响

沈欣悦

摘  要：以沪深A股上市的制造业企业为样本，结合外部政府研发资助与内部股权集中度两方面要素，探讨企业研发投入对技术创新效率的影响机制。研究认为企业研发投入与技术创新效率之间存在倒“U”型关系，即企业科研创新投入强度存在最优区间；政府研发资助显著正向激励技术创新效率，并在研发投入与创新效率之间起到负向调节作用；股权集中度则是无论对技术创新效率的激励作用还是对研发投入与创新效率的调节效应都不显著。

关键词：企业研发投入；技术创新效率；政府研发资助；股权集中度

中图分类号：F273.1  文献标识码：A  文章编号：1005-6432（2023）11-0000-05

[DOI]10.13939/j.cnki.zgsc.2023.11.000

1  前言

目前，中国由第三轮产业转移中的中低端产业接受国转变成为转出国，这预示着产业结构调整的政策已经初步取得成效。尽管改革开放与人口红利为中国制造业带来了全球第一的产值，高溢价的核心技术和知识专利仍保留在欧美发达国家手中，这使得中国处于全球加工链中获得附加值最低的区域。这一现状对企业技术水平提出要求，政府先后设立包括“973计划”、“863计划”等多项国家重点研发计划，以支持自主产权的获取。

科研创新投入不断提高，核心专利的产出情况却并未得到改善，这说明在投入与产出之间存在效率问题。我国研发创新领域目前存在三个问题：企业科技投入转化率低，政府研发资助利用率低，以及技术创新成果商业化程度低。现有研究大多强调研发投入，但考虑到研发创新的不确定性和高风险性，以及转化时间较长，只考察投入而忽略产出并不能正确的反映企业创新绩效。因此，本文以技术创新效率为研究对象，分析研发投入强度对技术创新效率的影响，将政府研发资助与股权集中度作为调节变量，以研究这两者在企业研发投入产出过程中的作用。2   文献综述

根据已收录论文的可视化分析，大部分学者对于企业科技创新的研究都是基于研发投入角度，但近年来对于技术创新效率的研究正在逐渐增加。对于研发投入与创新绩效之间的关系，相关研究普遍采用两阶段或三阶段DEA模型，认为企业创新研发全过程存在三个重要研究对象，即投入指标（研发资本投入与科研人才投入）、产出指标（专利数量与新产品产值）与绩效指标（技术创新绩效与商业化绩效）。李爽与陈庆江认为企业研发投入对科研创新效率有正向显著的促进作用，关于政府投入的调节效应，前者认为无有效影响，后者则认为存在负向调节作用。陈水娟认为研发投入与专利产出率存在倒“U”型关系，并考察了管理权激励与产权性质的调节作用。

已发表的文献中，技术创新效率和企业研发投入的主要影响因素基本相同，为政府资助强度（直接资金补助、间接优惠政策）、企业治理结构（两职分离率、董事会规模、股权集中度、高管激励情况）和企业基本情况（企业规模、产权性质、所在行业、企业运营情况），但不同学者研究结论的差异性较大。

郑延冰认为政府资助水平虽与企业研发投入指标显著正相关，但对企业研发效率并无显著促进作用。叶祥松认为在现阶段情况下，政府对于科技创新活动的支持存在门槛效应，知识创新与技术创新之间存在转化问题。周阳鹏认为内部控制对研发效率存在正向影响，由股权制衡度负向调节，国有企业性质正向调节。陈金勇认为管理层持股对于企业技术创新绩效的作用机制呈现倒“U”型动态特征，影响效应会随着持股比例增加由激励转为堑壕效应。Shilei Cao的研究结论为市场竞争和企业规模对两阶段创新效率具有显著的正向影响，产业出口强度和政府干预对两阶段创新效率具有负向影响。

已有研究成果缺乏对企业研发影响因素和研发效率影响机制整体性的考察。本文的研究思路在于：一是以企业研发投入为影响技术创新效率的主要变量，研究企业选择研发支出强度的最优区间；二是研究变量之间是否存在非线性关系；三是兼顾内外部视角，研究政府研发资助强度与股权集中度的调节作用。

3   理论回顾和假设提出

3.1  企业研发投入强度与技术创新效率的关系

目前已有文献存在三种假设，分别认为企业研发投入强度与技术创新效率存在正相关、负相关和非线性关系。我国企业目前总体研发投入程度较小，无论是企业知识存量还是科研基础设施都未达到最优水平，处于规模报酬递增状态，增加研发投入可以显著提高创新绩效。当企业研发投入超出一定程度时，认为其会产生“过犹不及效应”和“溢出效应”。一方面，优质项目的有限性和科研人才的稀缺性会导致超出一定程度的投入存在更大风险；另一方面，研发项目过多可能导致监管缺失和资源配置问题，因此认为企业创新研发投入对技术研发效率的正向影响存在某一阈值，并提出如下假设：

H1：企业研发投入对技术创新效率之前呈倒“U”型关系。

3.2   政府资助的调节作用

部分学者认为政府研发资助在企业研发投入与技术创新效率之间存在正向调节作用。一方面，政府研发资助减少了企业的融资约束，拓宽科研项目的选择范围，提高长线投资和增加技术要素投入的意愿。另一方面，企业获得来自政府的投资，暗示研發项目质量合格，且研发将会接受政府监督，为项目后续进展提供了保障，因此提出假设：

另一方面，政府投入的性质决定了比起经济效益政府更关心社会效益，事实证明政府科研资助更倾向于选择具有回收期长、盈利低、公共性质较强的项目，这样的项目虽然对国家整体科技水平有着积极影响，但在短期内并不能促进企业创新效率的提升，提出假设：

3.3   股权集中度的调节作用

根据委托代理理论，管理层存在操纵投资决策影响自己薪酬利润的倾向。当股权较为分散时，股东缺乏对企业的绝对控制，因此管理层和股东、大小股东之间存在较高的协调成本；同时，较为分散的股权决定了每个股东从决策中获得的利润都是有限的，易产生搭便车行为。根据利益收敛假说，大股东利益相关程度越高，越有动力对管理层的投资决策行为进行监督，提出假设：

：股权集中度在企业研发投入与技术创新效率之间有顯著正向调节作用。

另一方面，股权集中度过高时，大股东控制的资源增加，会导致双重代理理论中大小股东的利益均衡被打破。小股东一般倾向于获得短期既得利益，这与研发投资周期长风险大的特点相矛盾。而大股东可能产生寻租行为和关联交易等行为，也更易做出风险倾向型决策，影响项目的成功率和研发效率。因此，可提出研究假设：

根据上述理论分析与研究假设，本文提出如图1所示的理论框架：

4   研究设计

4.1  研究样本与数据来源

在行业分类中，制造业上市时间久、样本数量多，A股数据公开，接受证监会管控，因此本文使用的研究样本是来自沪深A股制造业的2136家上市公司。为保证严谨性，本文对样本进行筛选：一是删除了ST、*ST、PT类企业；二是上市时间不足年的企业；三是关键变量缺失的观察值；四是对连续性变量上下1%的极端值采取Winsorize处理。最终本文得到1272个样本数据，初始观测值11448个。相关数据主要来源于Wind数据库和CSMAR数据库。使用SPSS软件、Matlab软件和STATA 15.1软件进行统计分析。

4.2  变量定义与测量方法

4.2.1  因变量：企业技术创新效率（RE）

企业科研产出一般用两个指标衡量，一是专利申请或获取数，即技术创新产出；二是新产品产值或销售额，即商业化效率。考虑到技术研发时间，采用滞后两年的专利申请数作为科研产出指标。企业技术创新效率用专利申请数与企业研发支出的比值来衡量。

4.2.2   自变量：企业研发投入强度（INV）

企业研发投入强度用企业研发支出总额与企业总资产的比值来衡量。

4.2.3  调节变量

调节变量选用指标为政府研发资助强度（SUB）和企业股权集中度（CON）。政府研发资助强度用政府对企业相关科研补助总额与企业总资产的比值来衡量。企业股权集中度用前五大股东持股比例总和衡量。

4.2.4  控制变量

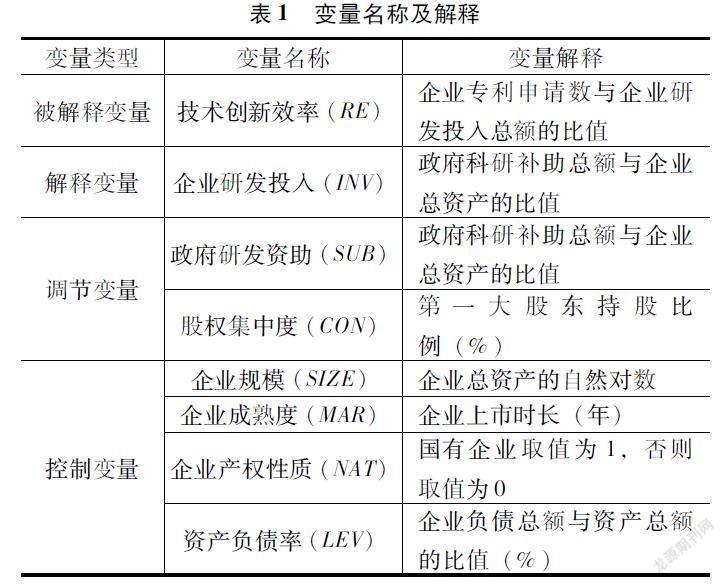
影响企业技术创新效率的因素有很多，本文仅研究制造业，因此对控制变量的选取简化处理，选择企业性质、企业规模、企业成熟度和资产负债率作为本文的控制变量，详见表1。其一，企业性质根据企业属性进行判定，将中央与地方国有企业判定为国有企业，民营、外资和集体企业判定为非国有企业；其二，一般认为，企业规模影响企业创新能力和企业承担创新投资风险的能力，因此本文用企业总资产取自然对数对其赋值；其三，企业成熟度用上市时长衡量，认为该因素影响企业科研经验的累积和创新配套设施的完善程度；其四，资产负债率可以用来衡量企业资金的利用能力，资产负债率过高可能导致研发初始投入的资金不足，或在研发过程中出现资金链断裂的情况；而资产负债率过低则说明企业外部资金运用能力较弱。

4.3   研究模型

基于理论分析和研究设计，本文构建如下模型进行假设验证。首先，为了验证企业研发投入强度与技术创新效率之间的关系，建立模型（1）：

为验证政府研发资助强度和股权集中度发挥的调节作用，在模型（1）的基础上进一步构建了模型（2）和模型（3）：

模型（1）为验证企业研发投入与技术创新效率之间是否存在非线性关系，加入了自变量的平方项；模型（2）、模型（3）为研究调节效应，加入了调节变量与自变量的交互项。为了避免平方项和交互项带来的多重共线性问题，对样本数据进行了去中心化处理。

5   实证检验结果分析

5.1   描述性统计

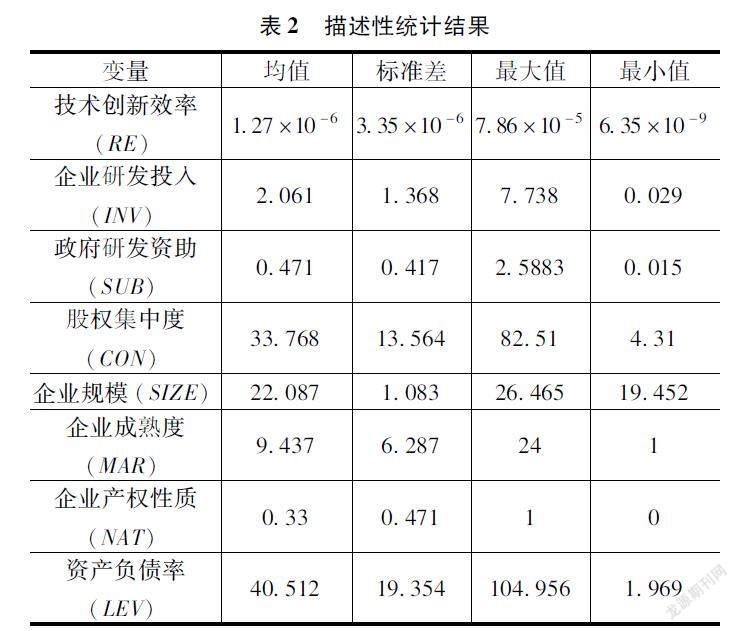
运用SPSS软件对主要变量进行描述性统计，结果如表2所示。企业研发投入强度均值为2.061，样本企业的研发绩效普遍偏低；在政府研发资助强度上，均值为0.471，最大值却达到了2.5883，表明政府研发资助呈现偏好性和差异性；股权集中度极端值差异较大，其均值则接近于中位数，说明股权集中与分散的样本企业数量基本持平。

就控制变量而言，企业规模的自然对数值差异较小，企业产权性质的频数划分也较为平均；就资产负债率指标而言，上市公司资产负债率应保持在40%～60%，而样本企业均值为40.05%，反映样本企业财务杠杆利用能力不足。

5.2   相关性分析

采用MATLAB软件计算各个变量之间的Spearman相关系数，从而检验其相关性，结果如表3所示。

变量间的相关系数基本均小于0.5，说明变量的选取并不存在严重多重共线性的问题，指标设计有较高的合理性和区分度。

5.3   回归分析

本文运用Stata 15.0软件对模型进行回归分析，回归结果如表4所示。由于模型存在平方项和交互项，在对变量数据进行中心化处理之后，在回归过程中对模型进行了多重共线性检验。若模型中的方差膨胀因子VIF>10，则认为该回归方程存在严重的多重共线性问题，实验结果显示不存在多重共线性问题。

5.3.1  企业研发投入强度对企业技术创新效率的影响

从模型（1）的回归结果可以看出，企业研发投入强度的一次项在1%的显著性水平上显著为正，平方项在1%的显著性水平上显著为负。这表明了企业研发投入强度与企业技术创新效率具有倒U型关系，与所作的矩阵散点图结果基本相符，研究假设H1得到了验证。企业研发投入强度较小会导致企业创新体系和技术基础设施不完善，研发监管缺失等问题。随着研发投入占比持续增加，创新研发出现规模效应，企业积累经验和科研人才获取，从而提高技术创新效率。然而，当企业研发投入占比过高时，研发资金的冗余和优质项目的有限性之间的不匹配，导致研发具有更高风险。

企业规模在1%的水平上显著为负，即企业规模的扩大会导致技术创新效率的降低。资产负债率在5%的水平上显著为正，说明随着企业融资约束指数值的降低，将为企业进行科研投入提供足够资金并扩大可供选择的科研项目范围，带来技术创新效率的提高。