基于FDD法的模态参数连续自动识别及 频率变异性分析
王晓光,马 明,高林丽,党李涛
(1. 长安大学 公路学院,陕西 西安 710064; 2. 中交第一公路勘察设计研究院有限公司,陕西 西安 710075)
0 引 言
模态参数能反映出桥梁运营的性能[1],同时也是桥梁评估、模型修正、损伤评估的基本指标[2-4],故模态参数识别一直都是桥梁健康监测的研究热点[5]。大量长期的模态参数是评估桥梁服役性能和性能演变规律的重要基础[6],其一般是通过分析由桥梁健康监测系统采集的结构动力响应数据获得。由于桥梁健康监测数据存在连续、量大等特点,模态参数连续、自动识别逐渐成为学界关注的重点[7]。
实时在线模态参数识别存在着困难,现有桥梁健康监测系统通常采用实时不间断采集结构动力响应数据,并将其按照一定规则进行存盘,最后再通用人工处理手段得到结构的模态参数。在数量巨大、时间较长的模态参数需求下,人工识别过程很难满足实际需求,急需找到一种合适方法实现模态参数连续、自动的识别。连续自动识别要解决两个问题:① 自动识别方法;② 监测数据连续自动读取流转。
模态自动识别是模态参数连续自动识别的核心。桥梁结构模态识别是基于实际的结构响应,采用数学方法并结合系统论和结构动力学基本原理的状态识别过程。模态识别方法分为时域法、频域法和时频域法[8],其中:时域法中的随机子空间法[9]、频域法中的频域分解法(frequency domain decomposition, FDD)[10]和时频域法中的小波分解法[11]运用得最为广泛。随机子空间法对密集模态具有较好的识别效果,但存在虚假模态问题,需要借助稳定图像结合人工干预才能到达较好的识别效果[5, 12],许多学者提出大量算法实现了稳定图像的自动识别[12-14],但由于随机子空间法本身计算效率不高,且稳定图像自动识别过程中往往需要大量迭代,因此基于稳定图像的自动识别方法效率较低;小波分解法的识别效果很大程度上依赖于小波基、分解尺度等变换参数的选择,人工干预较多,不适合自动识别;FDD不需要过多的人工干预,且计算效率较高,物理意义明确[8],故分析FDD的自动识别过程对桥梁健康监测数据分析很有必要。从识别过程而言,频域分解法的核心是选取奇异值分解曲线的峰值,并用人工挑选方法选出合适的峰值[15],从而确定结构的真实模态参数,该方式需要人工干预,无法实现自动识别。由于噪声干扰存在,奇异值往往不是光滑曲线,存在的大量噪声干扰会引起毛刺峰值,严重影响了工程人员的选择。如何剔除虚假峰值并自动挑选出真实峰值是基于FDD模态参数自动识别要克服的主要难点。
数据自动获取是模态参数连续识别的基础。通过连续自动获取结构监测数据并传递给自动分析核心,才能实现模态参数连续自动识别。数据自动获取方式与健康监测系统数据存储方式密切相关,数据自动获取的关键是识别数据存储的标准格式。
笔者通过深入分析基于FDD模态参数识别过程的特点,提出了融合奇异值滤波、波峰波谷检测、差异指标计算和自动聚类方法的FDD模态参数自动识别方法和模态参数自动识别框架;并将所提出该方法融入到自动识别框架中,实现了模态参数连续自动识别;最后通过某斜拉桥实测数据,验证了所提出方法的可行性。
1 频域分解法
FDD通过频率响应函数在特征频率处产生的峰值特性来识别参数,并通过奇异值分解将结构离散为单子度系统,实现了模态参数的识别。首先假定结构输入为高斯白噪声,利用结构响应求解功率谱密度函数,通过SVD分解,得到结构单自由度系统的响应集合,每个独立模态即为响应奇异值分解后的每一列元素。
系统输入u(t)和输出x(t)之间的关系如式(1):
Sxx(jω)=H(jω)*Suu(jω)H(jω)T
(1)
式中:Sxx(jω)为输出x(t)的PSD矩阵;H(jω)为频率响应函数(FRF)矩阵;Suu(jω)为输入u(t)的功率谱密度(PSD)矩阵。
若输入u(t)的PSD为常数,则有Suu=Ruu。对于小阻尼结构,输入功率谱密度矩阵如式(2):
(2)
式中:αi为常数。
由监测响应数据计算Sxx(jω),并进行SVD分解,如式(3):
Sxx(jω)=Φ∑ΦH
(3)
式中:Φ=[φ1,φ2,…,φr],为包含有r个奇异向量;ΣΦ为对角矩阵,包含有r个奇异值,与单自由度的PSD值对应。
在PSD函数图中,每个峰值均代表结构的固有频率,在第i个峰值ωi附近,该阶模态将起主导作用;此时,式(3)右侧第一个奇异向量φ1即为模态振型估计;ΣΦ中第一个不为0的奇异值即为结构的固有频率。
2 FDD模态参数自动识别原理
基于FDD模态参数自动识别核心是从奇异值曲线所有峰值中自动选取真实模态参数对应的峰值,并由真实峰值得到结构的真实模态参数。要实现模态参数自动识别,主要解决:虚假峰值干扰、峰值自动识别和真实峰值选取。笔者分别通过滤波、差异指标计算和自动聚类方法解决上述3个问题,达到模态参数的自动识别。
2.1 奇异值滤波
由于环境噪声干扰,随机环境下的结构奇异值曲线并不是光滑曲线,而是在峰值中间夹杂着大量毛刺峰值。对于FDD而言,要通过寻找奇异值曲线峰值的方法来提取对应的结构模态参数,因此剔除噪声引起的毛刺峰值干扰是首先要解决的问题。
奇异值曲线是一维数据曲线,笔者引入3点前、后向运动均值滤波算法来剔除环境噪声所引起的奇异值毛刺现象。
假设一组信号为Sn={s1,s2, …,sn},3点均值滤波计算如式(4):
(4)
前、 后向滤波的区别是:前向滤波i从2开始增大至n-1;后向滤波i从n-1逐渐减小至2。
2.2 波峰波谷检测
自动识别核心是自动识别奇异值曲线中的真实波峰,从而自动索引得到波峰对应的模态参数。为给后续自动识别算法提供数据,笔者采用峰值检测方法同时检测得到滤波的奇异值曲线波峰值和波谷值。
波峰检测计算如式(5):
P(n)=S(n):S(n-1)
(5)
对应峰值位置计算如式(6):
Lp(i)=n:S(n-1)
(6)
波谷检测计算如式(7):
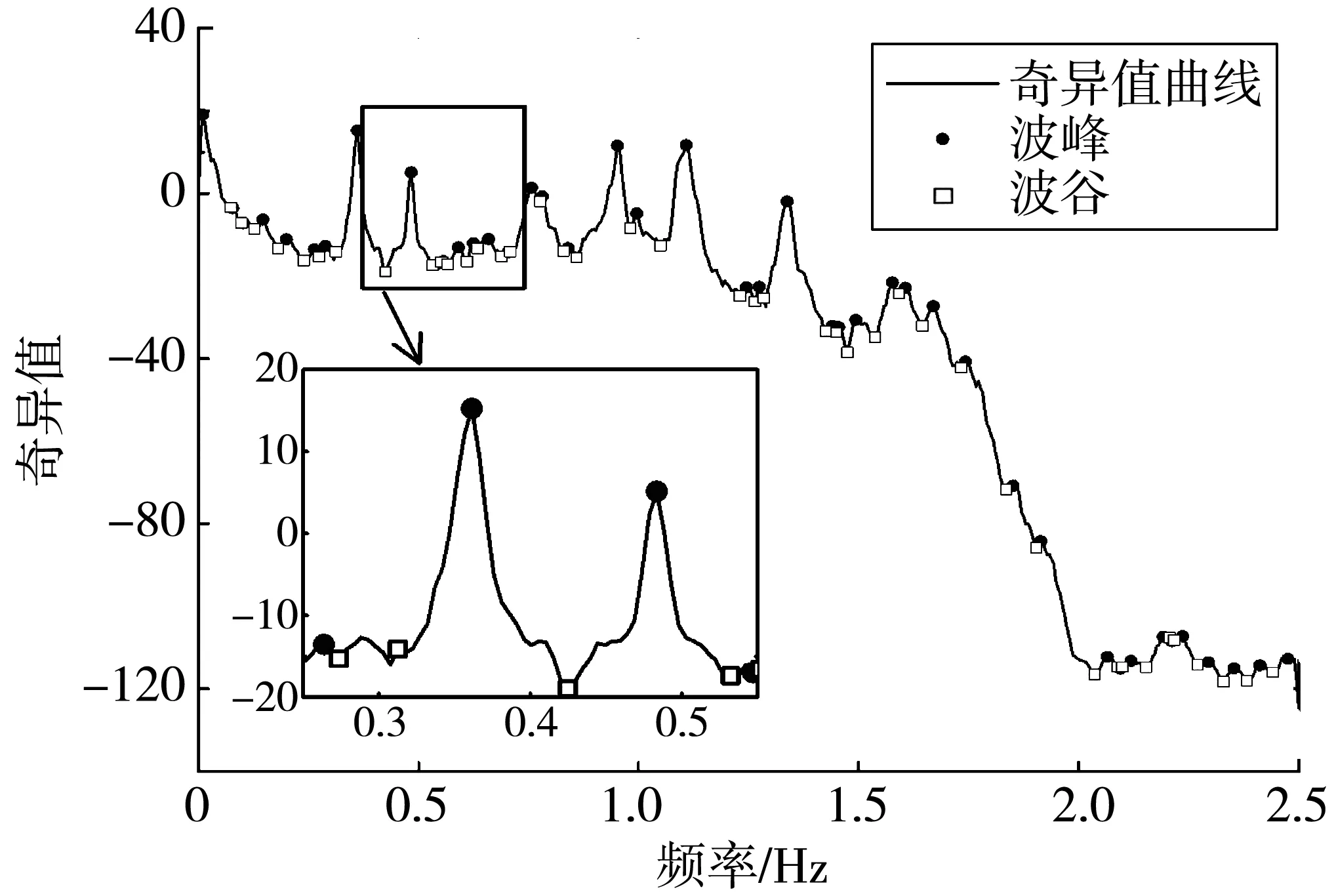
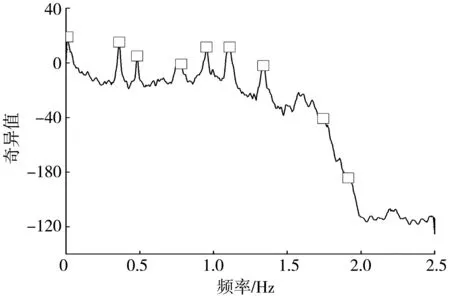
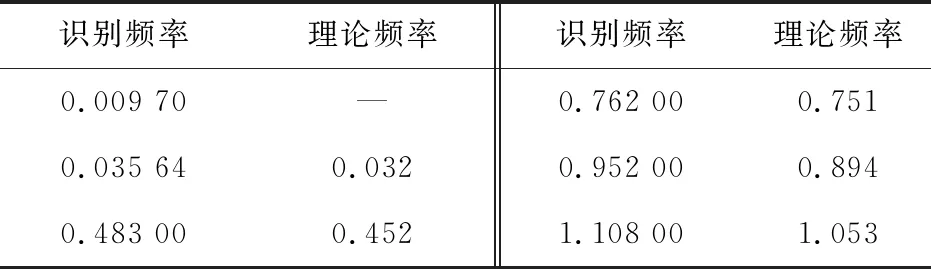
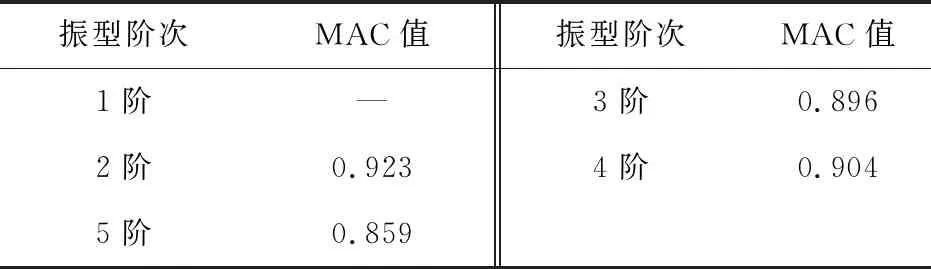
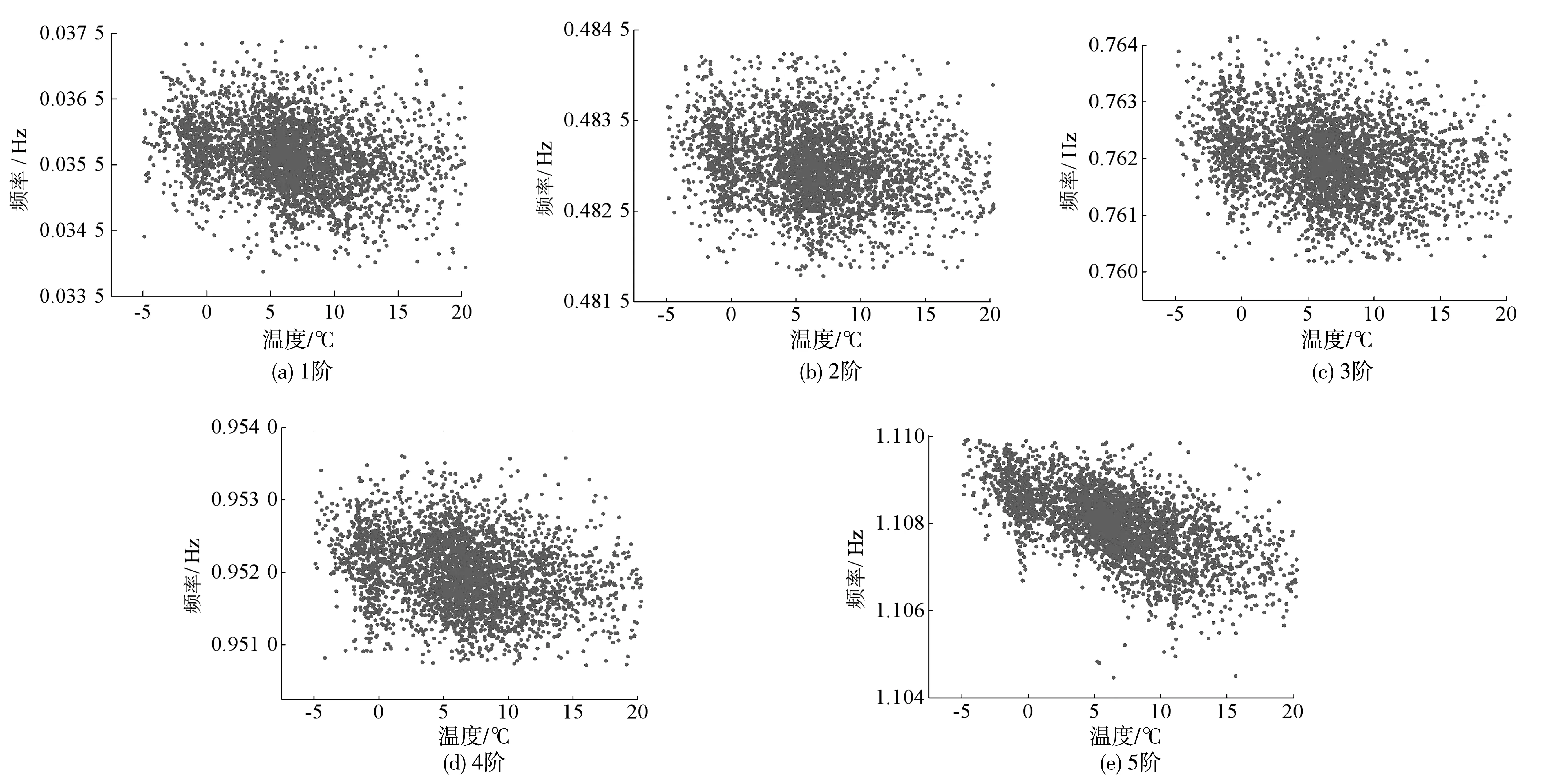
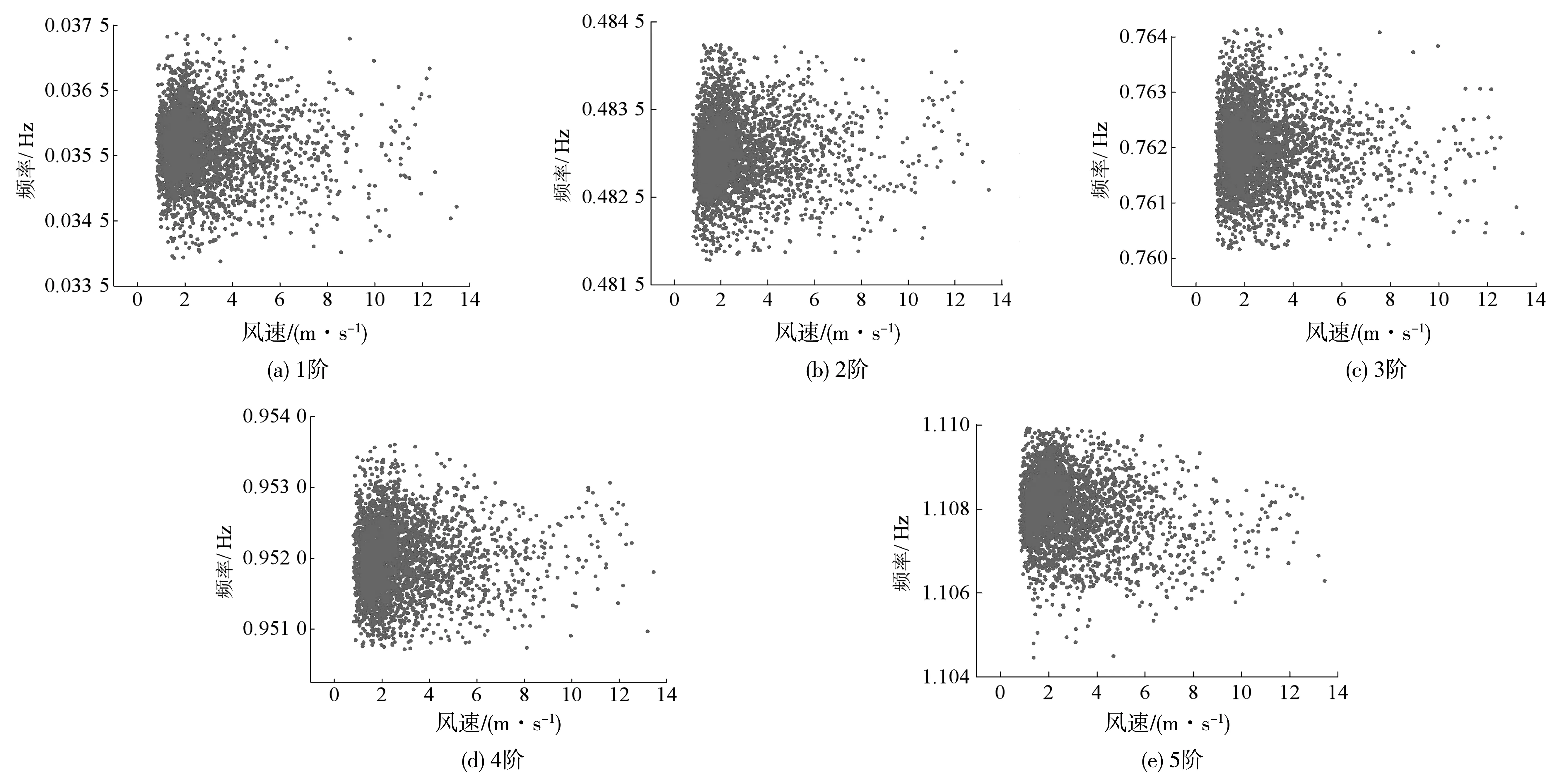
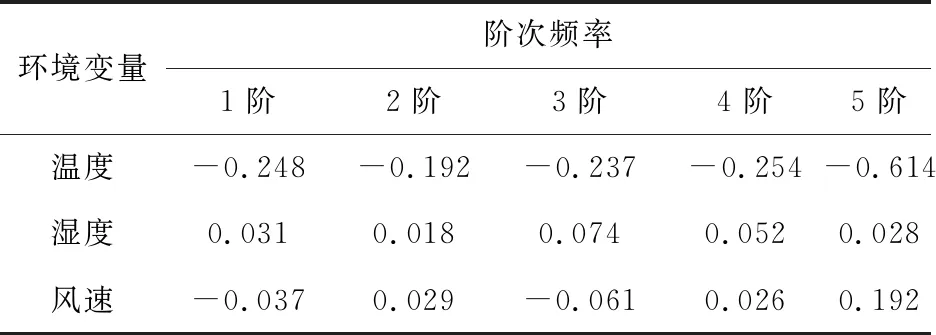
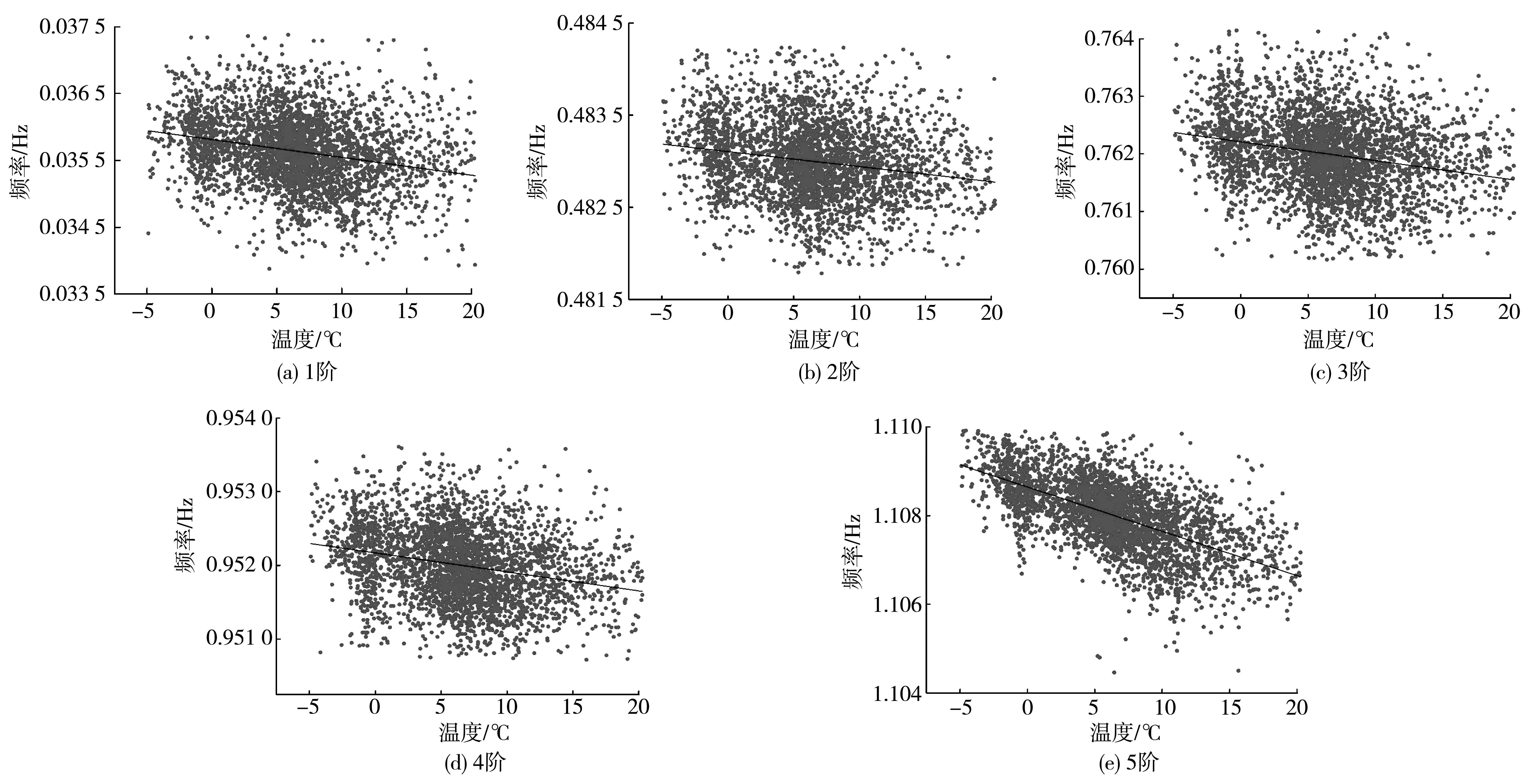
V(n)=S(n):S(n-1)>S(n) (7) 对应波谷位置计算如式(8): Lv(i)=n:S(n-1)>S(n) (8) 通过峰值检测过程虽能得到奇异值曲线的所有峰值,但并不是所有峰值都对应真实的模态参数。故基于峰值检测的FDD模态参数自动识别方法一个重要的方面就是甄别峰值中的虚假峰值。 在环境随机激励下,虽然存在噪声干扰,但结构响应在真实模态参数的频带附近会出现较大峰值。即在奇异值曲线中,真实模态参数对应的奇异值峰值较高,而噪声所引起的虚假峰值较低。由于不同频带范围的结构响应信号能量不同,在不同频带范围内的奇异值整体大小有所差异。在某些频带内,即使有较明显(真实模态峰值)的峰值,也会因整体能量较低而导致峰值较小。 为识别真实峰值,笔者提出用波峰波谷差(valley-peak difference,Dvp)指标作为真实峰值的筛选指标。Dvp指标是表示波峰和波谷之间差异的指标,通过Dvp指标大小可得到波峰 “深度”,如图1。 图1 Dvp指标峰值判断 通过Dvp指标可识别得到所有真实模态参数所对应的相对较高的峰值,但Dvp指标是一个包含所有波峰与波谷的差值,要实现模态参数的自动识别,就需要从中自动挑选出真实模态参数所对应的Dvp指标。 真实模态参数对应的奇异值波峰相较于波谷较高,因此其对应的Dvp较大;反之亦然。为自动得到Dvp较大的真实峰值,笔者引入K-均值聚类(K-mean)法,通过K-means聚类法对Dvp指标进行自动分类,自动挑选出真实峰值所对应的Dvp指标。其基本原理如下: 假设Dvp指标样本为X=(x1,x2,…,xn),样本间的相似度通常用距离d(xi,xj)来度量,距离的计算如式(9): (9) K-means聚类法使用误差平方和准则函数来评价其聚类性能,聚类的目的是使其误差平方和最小。假设n个样本被分成k类,且每个类的聚类中心分别为(c1,c2,…,ck),属于各个聚类的数据子集分别为(P1,P2,…,Pk),则误差平方和E定义如式(10): (10) K-means聚类法通过迭代过程不断优化聚类中心和各类中的元素,直至E收敛至最小。其迭代聚类过程如下: 1)将所有对象随机分配到k个非空的簇中; 2)计算每个簇的平均值,并用该平均值代表相应的簇; 3)根据每个对象与各个簇中心的距离,分配给最近的簇。 4)重复2)、3),直至E最小则停止迭代,并将聚类得到的值作为最终结果。 K-means聚类法首先需要设定聚类数目,聚类数目决定了数据样本可被分为几类。借助K-means聚类过程,将聚类数目设为2,所有Dvp指标可自动分为两类,Dvp指标较大类代表真实模态参数的奇异值峰值,Dvp指标较小类代表虚假模态参数的类的峰值。通过索引Dvp指标较大类的峰值,就能得到真实模态参数对应的奇异值峰值,进而识别得到真实模态参数。 模态参数自动识别只是解决了模态参数自动识别的核心算法理论问题,连续自动识别则是涉及数据如何连续自动流转的系统性问题。桥梁健康监测系统的监测数据一般采用标准格式的离线文件存储,不同监测类型的监测数据一般以小时进行存储,然后按照天、月为单位存储在文件夹中,不同监测类型监测数据通过不同文件后缀名进行区分。通过搭建模态参数连续自动分析框架,实现监测数据的连续自动读取和流转,并结合自动识别算法,实现模态参数连续自动识别。 建立连续长期的离线监测数据自动读取模块,通过输入文件保存路径和加速度文件后缀,自动识别保存的加速度离线文件,并提取加速度数据;再搭建模态参数自动识别模块,并融入数据自动读取模块,模态自动识别模块不断从数据读取模块获取离线监测数据用于模态参数自动识别;最后为整个数据自动读取和自动分析搭建循环框架,使得整个分析过程能自动进行。笔者设计的自动分析框架每次能连续自动分析一个月的数据,其框架如图2。 图2 连续自动识别框架 通过连续自动识别框架实现监测数据不间断提取,通过前、后向均值滤波最大、最小值检测,Dvp指标计算和K-means聚类法;实现了虚假峰值的剔除,真实峰值的自动选取;从而实现了模态参数的自动识别。基于FDD模态参数连续、自动识别过程如下,整体流程如图3。 图3 FDD法模态参数连续自动识别流程 1)输入文件路径和文件后缀、最小数据量和分析间隔时长,自动确定数据分析次数和数据读入量; 2)对原始信号进行滤波处理,并采用FDD求解奇异值分解曲线; 3)对奇异值曲线进行前、后向均值滤波处理,剔除大量噪声干扰引起的虚假峰值; 4)通过峰值检测算法检测得到滤波后的奇异值曲线的波峰和波谷; 5)计算Dvp指标; 6)采用K-means聚类法得到真实模态参数对应的奇异值峰值; 7)根据得到的真实模态参数奇异值峰值,得到对应的真实模态参数; 8)进行下一次分析。 笔者以某座桥梁为例进行分析。该桥梁是一座(50+110+380+110+50)m的双塔钢箱梁斜拉桥,如图4(a)。采用MIDAS Civil软件建立理论计算模型,其中主梁、索塔采用梁单元模拟,斜拉索采用只受拉桁架单元模拟;全桥共862个节点,738个单元,有限元模型如图4(b)。 图4 桥梁概况(单位:m) 该桥建成之初便安装了健康监测系统。全桥共38个加速度传感器,其中主梁安装竖向加速度传感器22个。健康监测系统将采集的结构加速度响应数据按小时存储为离线文件,本次分析采用的是2021年1月全月的加速度数据。 为尽量获取环境效应对结构模态参数的影响,设定为每次连续自动分析20 min数据,两次分析间隔时间为10 min,每2 h之间数据不重叠,即每1 h分析可得到5组模态参数。 采用FDD对滤波后的加速度数据进行分析,得到经FDD法计算得到的奇异值分解曲线,如图5。图5(a)给出部分传感器通道数据的奇异值曲线,图5(b)表示其中两条奇异值曲线。 图5 奇异值曲线 由图5可看出:奇异值曲线在一些频带范围内出现峰值,这些峰值对应的模态参数极有可能是结构的真实模态参数;原始奇异值曲线除了在个别频率处出现较大峰值,在峰值之外还存在大量的较小峰值点,这些峰值是结构响应中噪声干扰引起的。 采用三点前、后向线性均值滤波方法对奇异值曲线进行滤波,图6表示滤波前后奇异值曲线的变化。由图6可看出:滤波前环境噪声引起的奇异值曲线大量毛刺峰值被剔除,滤波后的奇异值曲线在毛刺峰值处变得相对平滑;同时滤波前后的真实峰值位置没有发生变化,说明三点前、后向均值滤波很好保留了奇异值曲线的真实峰值位置。 图6 滤波前后奇异值曲线 采用峰值检测算法识别滤波后的奇异值曲线。图7表示对滤波后的奇异值曲线进行波峰、波谷检测结果。由图7可看出:波峰、波谷检测过程识别得到了滤波后的奇异值曲线所有的波峰、波谷,检测算法识别得到了所有潜在对应真实模态参数波峰,但同时也包含大量虚假波峰。 图7 波峰波谷检测 通过得到的所有波峰、波谷奇异值来计算Dvp指标。图8表示所有波峰和波谷计算得到的Dvp指标。由图8可看出:Dvp指标分布在不同的区间范围,Dvp指标较大值是奇异值分解曲线中的较高峰值,这些峰值是潜在的真实模态峰值;Dvp指标较小值是奇异值分解曲线中的较矮峰值,这些峰值可能是因噪声干扰引起的虚假峰值或因环境激励能量有限所产生的弱模态。 将K-means聚类法用于所有Dvp指标进行聚类,并取k=2,如图8。图8中:虚线表示对聚类结果划分,所有Dvp指标根据其值大小被分为两类,虚线以上的为一类,是Dvp指标较大的一类,表示了潜在真实模态参数对应的奇异值曲线峰值;虚线下的Dvp指标较小,对应奇异值曲线中较矮的峰值,即绝对噪声干扰所引起的虚假峰值。 图8 Dvp指标聚类结果 图9表示聚类结果中Dvp指标较大的一类对应的奇异值波峰位置。由图9可看出:自动识别得到了所有潜在真实模态参数对应的奇异值峰值;但除了峰值较高的奇异值峰值外,在频带1.5~2.0内同时识别到了两个峰值,但很明显这两个峰值都是虚假峰值。这是由于结构响应信号在高频带范围内的能量减少,所对应的奇异值迅速减小,奇异值曲线在急速下降过程中没有出现反复波动,导致波峰、波谷奇异值差别较大,进而引起Dvp指标较大,在自动识别过程中被识别为真实峰值。为避免错误,在最终挑选识别结果时,尽量避免靠近滤波截止频率的频带峰值,应挑选前几阶作为最终识别结果。 图9 自动识别得到的真实峰值 识别得到的前6个奇异值峰值对应的频率和振型分别如表1和图10。实测识别振型与有限元理论振型之间的相关性采用模态置信准则(MAC)MMAC进行验证,MAC的计算如式(11),验证结果如表2。 表1 频率识别结果 图10 识别振型结果与理论振型 MMAC({φi},{φj})= (11) 其中:第1阶振型明显异常,说明奇异值曲线中该波峰对应的模态参数为虚假结果。噪声干扰所引起的奇异值曲线虚假峰值一直是困扰业界进行模态参数识别的难点,如何从奇异值曲线中自动剔除峰值较高的虚假峰值,还需进一步探讨。 表2 实测识别振型与有限元理论振型的MAC值 此外,在识别过程中会出现因数据信噪比较差或算法输入参数选择不当而产生峰值较低的虚假模态,以及因环境激励能量有限产生的弱模态。对于峰值较低的虚假模态和弱模态区分,一方面根据先验知识确定频率分布范围,选择合适的滤波范围,把信号集中于需要关注的频带内;另一方面,可使用某些模态验证标准,如模态保证准则(MAC)或平均相位偏移(MPD)等标准。对于处于结构频率附近内虚假模态或能量非常低的弱模态,可采用动态滑窗法对其连续多次识别,并将识别到的模态参数结果进行统计和聚类,这就在很大程度上可以区分峰值较低的虚假模态和弱模态。 由上述可知,笔者所提出的FDD模态参数自动识别算法能自动检测得到奇异值分解曲线真实模态参数对应的峰值,同时能剔除因噪声干扰所引起的虚假峰值,可自动识别得到结构模态参数。但该方法仍无法解决能量较高虚假峰值的辨别问题,能量较高虚假峰值的辨别方法还需寻找其他方法。 基于连续分析框架,连续自动识别该桥梁一个月的监测数据,1 h可得到5组结果,1月份共得到3 720组结果。首先剔除第1阶识别的虚假结果,然后分析其余5阶识别频率与环境的相关性。 图11表明了前5阶识别频率与温度的关系。由图11可看出:各阶频率与温度均成负相关,且随着阶次升高,其相关性有变强趋势;第5阶频率与温度相关性明显强于前4阶,说明高阶频率受环境影响更明显。 图11 温度-频率关系 图12表明了湿度与频率的相关性。由图12可看出:前5阶频率与湿度的相关性均较小。与温度相关性不同的是,第5阶频率与湿度没有表现出明显的相关性,说明湿度对结构频率几乎没有影响。 图12 湿度-频率关系 图13表明了风速与结构频率的相关性。与湿度相同,前5阶结构频率与风速没有表现出较强的相关性,第5阶频率与风速表现出较弱相关性。 为更好地说明结构频率与环境的相关性,笔者采用Pearson系数对温度、湿度与风速的相关性进行量化。Pearson系数衡量了线性相关关系。当Pearson系数绝对值大于0.4时,两者具有中等程度及以上相关性;当Pearson系数绝对值小于0.4大于0.2时,为弱相关。表3给出不同阶次频率与温度、湿度和风速的Pearson系数。 图13 风速-频率关系 表3 不同阶次频率与环境变量皮尔逊系数 由表3可看出:温度与频率的Pearson系数明显大于湿度与风速,且均为负值,说明温度与结构频率成负相关,这与图11的结果一致。第5阶频率与温度的Pearson系数绝对值明显大于前4阶,说明该阶频率受温度的影响较大。湿度与频率的Pearson系数均趋近于0,说明湿度与结构频率的相关性不强,除第5阶频率与风速具有较弱相关性外,其余4阶与风速的Pearson系数均较小,这说明风荷载对桥梁低阶频率几乎没有影响,风荷载只对高阶频率具有较弱影响。 温度与结构频率Pearson系数大于0.2,存在弱相关;其中温度与结构第5阶频率为-0.614,具有强相关性。因此,笔者采用线性回归方法建立了温度与频率的相关性模型,并剔除识别频率中的温度效应。其中1~5阶的线性相关模型如式(12): (12) 对建立的1~5阶线性相关模型回归方程进行显著性检验(α=0.05),检验结果如表4。由表4可知:在给定显著性水平α=0.05时,不同阶次回归方程|T|均大于tα/2(n-2),认为线性回归显著。 表4 不同阶次回归方程显著性检验结果 回归线性模型与频率散点如图14。由图14可看出:即使剔除频率结果中的温度效应,识别频率结果仍在一定范围内波动,这是由于计算误差及车辆、信号干扰等随机因素所引起的。对于背景桥梁,1阶频率波动超过10%,但这些随机因素很难量化,且其中的干扰机理也不明确。结构频率是进行结构评估、模型修正的重要参数,如何从离散识别结果中提取合适的具有代表性的识别结果仍需要进一步研究。 图14 频率-温度回归结果 1)所提出的模态自动识别能实现基于FDD模态参数自动识别。通过前、后向均值滤波能剔除因大量噪声干扰所引起的虚假噪声峰值和平滑奇异值曲线,同时保留真实峰值;通过波峰、波谷检测,并结合提出的Dvp指标能准确识别得到奇异值曲线峰值;通过K-means聚类,能将Dvp指标自动划分成真实峰值和虚假峰值,能自动实现真实峰值的自动选取,并自动识别得到模态参数。 2)提出融合模态参数自动识别算法连续自动分析框架能解决实际桥梁健康监测系统离线监测数据的连续自动分析问题,通过背景桥梁的一个月的连续分析,验证了该框架和所提出自动识别算法的可行性。 3)结构频率受环境温度影响较大,受湿度和风荷载影响较小。结构频率与环境温度成负相关关系,采用线性回归方法能剔除识别频率中的环境温度影响效应。由于随机环境因素影响,识别结构频率具有较大的离散性,如何解决离散性问题仍需进一步研究。2.3 Dvp指标计算


2.4 基于K-means聚类法的真实峰值自动识别
3 模态参数自动识别框架
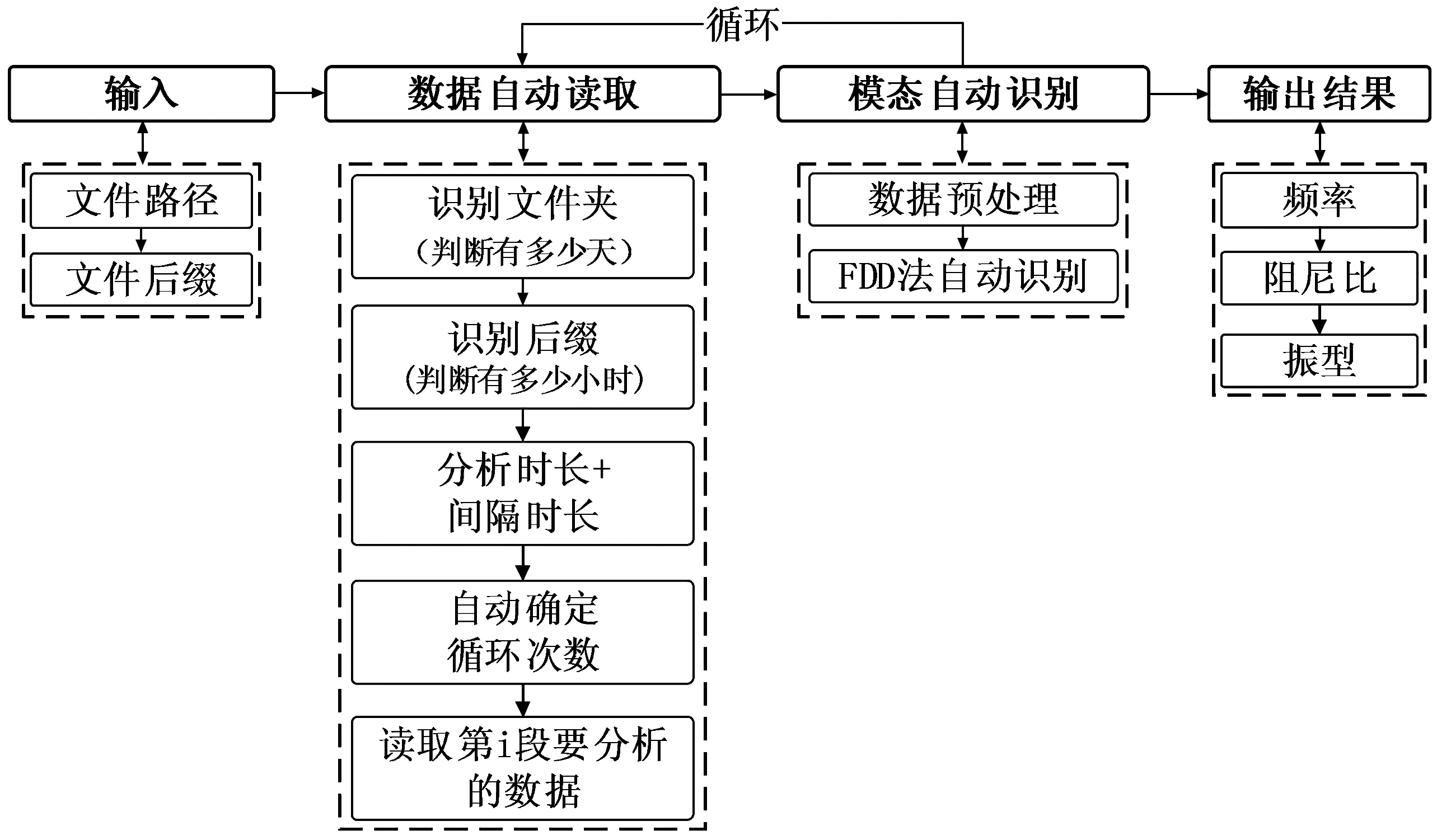
4 基于FDD模态参数自动识别
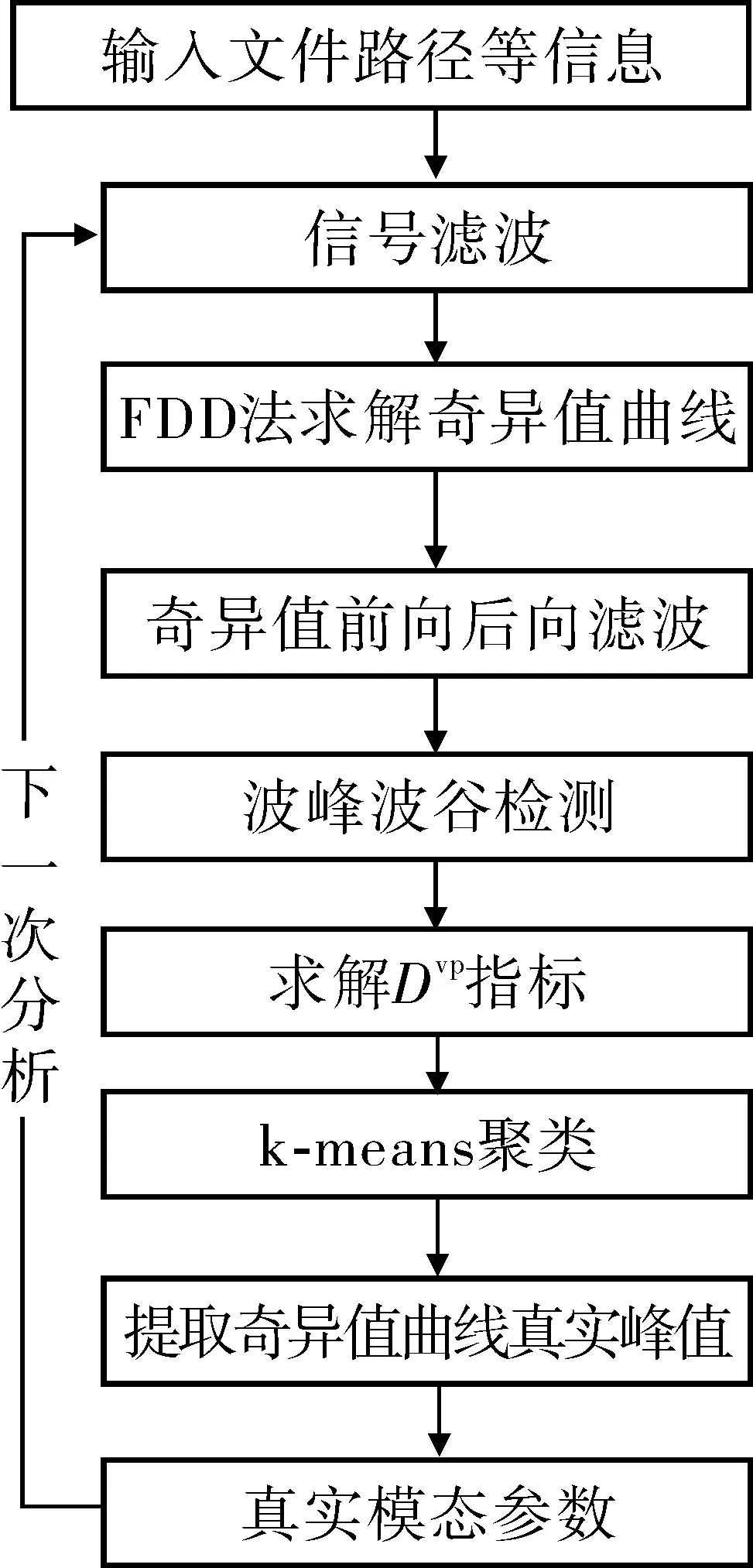
5 工程算例
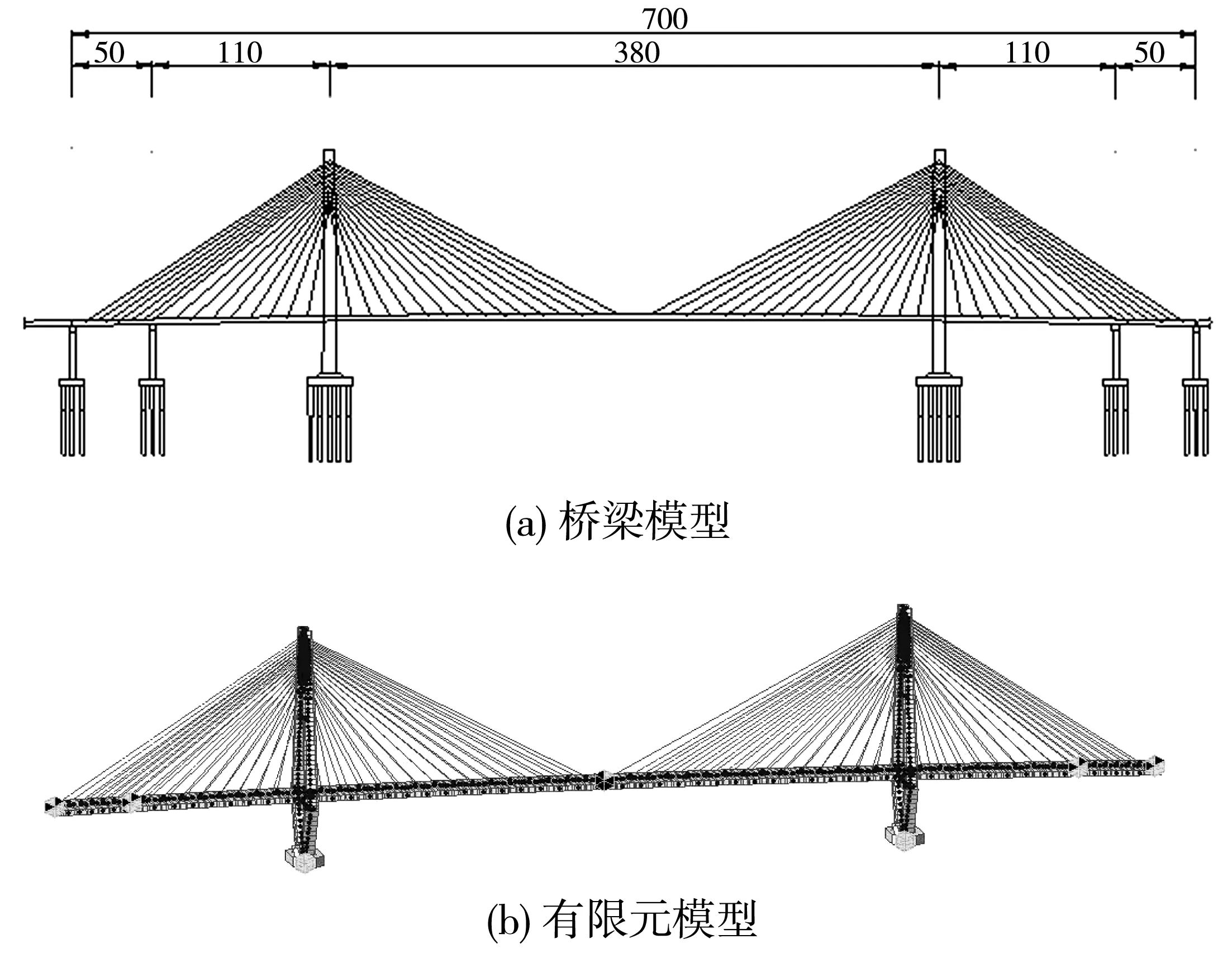
5.1 模态参数自动识别
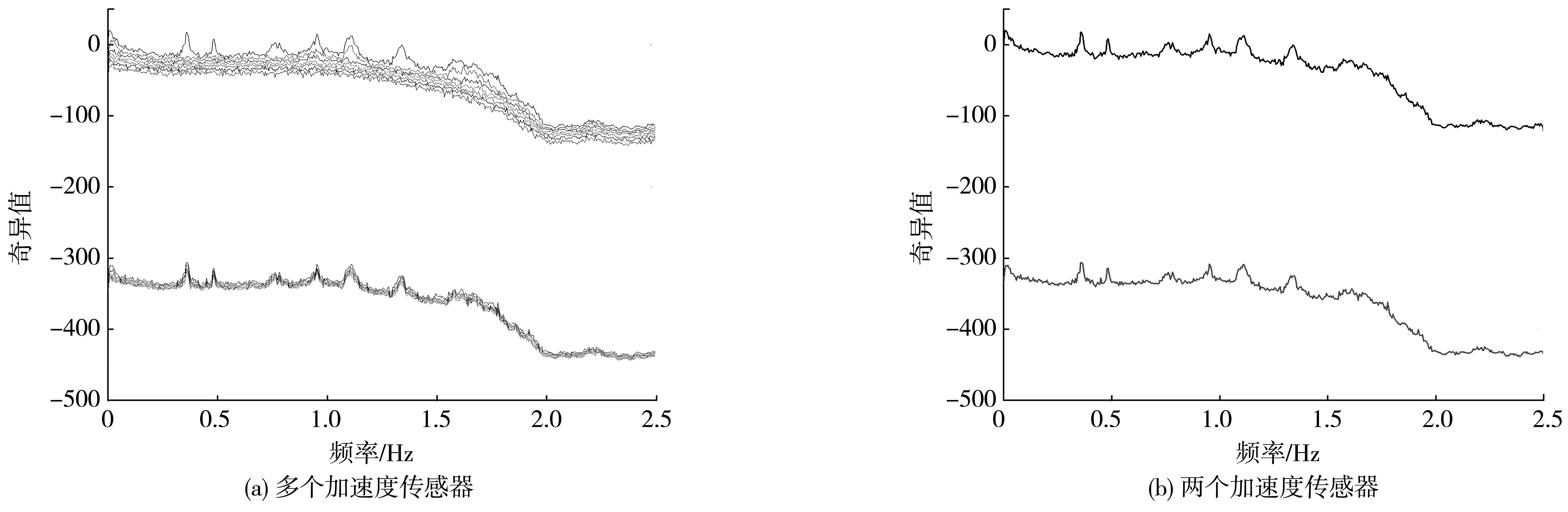



5.2 识别频率结果分析


6 结 论

