郭家沱长江大桥主缆状态影响参数敏感性分析

熊桂开,王 辉,陈翰新,何旭东

(1. 重庆大学 土木工程学院,重庆 400045; 2. 重庆市勘测院,重庆 401121; 3. 西南交通大学 土木工程学院,四川 成都 610031; 4. 重庆中建郭家沱大桥建设运营管理有限公司,重庆 400020)

悬索桥跨越能力大、造型优美,是现代桥梁的重要形式之一[1]。公轨两用悬索桥与公路悬索桥相比,具有荷载大、结构受力复杂、行车舒适性要求高等特点,因此对桥梁线形精度的要求也更高。主缆作为悬索桥的主要承重构件,是控制悬索桥成桥线形的重要因素,当悬索桥主缆架设完成后,主缆的实际成桥线形已经确定,后期施工中无法对主缆进行调整,因此在悬索桥的施工控制中,空缆线形是主缆施工的重要控制指标[2-5]。主缆的空缆线形受许多因素影响。例如:架设时主缆温度、桥塔预抬高值、主缆钢丝制造误差(钢丝直径制造误差、钢丝弹模制造误差等)、钢桁梁重量误差等。

为确保成桥后的桥梁线形符合设计要求,在进行悬索桥主缆施工控制时,精准计算出主缆的空缆线形对指导主缆架设施工至关重要[6]。笔者以一座在建大跨度公轨两用悬索桥为例,基于BNLAS软件,采用空间几何非线性有限元分析方法,从架设时的主缆温度、桥塔预抬高值、钢丝弹性模量、钢丝直径、钢桁梁重量误差等参数来分析其对主缆状态的影响。

1 项目概况

郭家沱长江大桥是重庆市六纵线横跨长江的节点性工程。该桥为(67.5+720+75)m的单孔悬吊双塔三跨连续钢桁梁公轨两用悬索桥。大桥采用双层布置,上层为8车道城市道路,设计时速80 km/h;下层为双线轨道交通,线间距5.2 m,最高设计运行速度100 km/h。主缆采用预制平行钢丝束股法(PPWS)形成,矢跨比为1∶9,两根主缆中心距为38 m,通长索股133股,每根索股由127根直径5.45 mm、公称抗拉强度1 860 MPa高强镀锌钢丝组成。吊索仅在中跨设置,采用公称直径5.00 mm、公称抗拉强度1 860 MPa高强镀锌钢丝组成,吊点标准间距为15.0 m。加劲梁采用正交异性钢桥面板桁结合钢桁梁,主桁架为带斜撑的三角形桁架,主桁架高度12.7 m,标准节间长度15.0 m,两片主桁中心间距为17.0 m。桥跨布置见图1;有限元模型见图2。

图1 郭家沱长江大桥桥跨布置(单位:cm)

图2 郭家沱长江大桥有限元模型

2 主缆状态影响参数分析

2.1 温度对主缆线形的影响

温度荷载是悬索桥的主要荷载之一。大跨度悬索桥为柔性结构体系,温度变化会引起结构状态的显著改变。国内学者对此进行了大量研究,张永水等[6]通过分析得出温度对悬索桥线形有较大影响的结论,在悬索桥空缆架设施工中,温度不仅会改变主缆索股长度,还会引起主塔偏位;范杰等[7]针对悬索桥空缆线形对跨径及温度变化敏感的特点,从理论和工程实践上系统性的阐述了该影响。

根据郭家沱长江大桥设计资料,设计基准温为20 ℃,为精确计算架设时主缆温度变化对空缆线形的影响,结合桥位处施工环境,分别采用架设温度为0、10、20、30、40 ℃这5种温度工况,计算分析架设时主缆温度对空缆线形影响,计算结果采用相对设计基准温度(20 ℃)的变化值表示,如表1。

表1 主缆温度对主缆空缆线形影响

从表1可知:当架设时主缆温度每升高10 ℃,计算出的主缆空缆线形中跨跨中矢高将降低0.295 m,边跨跨中矢高将降低0.034 m;中跨空缆线形受温度影响较大,边跨空缆线形受温度影响较小。这是因为在不同架设温度下,得出的索鞍预偏量不同。若鞍座固定,温度变化引起单孔悬吊悬索桥中跨主缆力变化小,边跨主缆力变化大;若鞍座放开,为保证塔顶两侧主缆水平力达到平衡,从而边跨主缆矢高变化小,中跨主缆矢高变化大,故中跨跨中空缆矢高相较于边跨受架设温度影响大。

悬索桥施工控制一般选择在结构各部分温度尽量接近的情况下进行,并在架设时要对环境温度场进行监测,其目的是为主缆线形调整、监控计算提供参数,精确计算并指导主缆的空缆架设,保证其架设精度要求[8]。从变化规律中可看出:主缆跨中矢高变化值与架设温度近似为线性关系,可用式(1)表达。

St=S0+K(T0-T)

(1)

式中:St为任意温度下跨中矢高值;S0为设计基准温度下跨中矢高值;T为丝股架设期间平均温度;T0为设计基准温度;K为主缆架设温度影响系数(本桥可近似取值K=0.029 6)。

2.2 桥塔预抬值对主缆线形的影响

混凝土桥塔在索鞍传递的上部结构竖向荷载作用下,将产生弹性压缩,随着时间变化,也将产生收缩变形及徐变。为确保成桥后塔顶标高满足设计要求,施工时会将塔顶标高在设计标高状态基础上进行预抬[9]。如:万州新田长江大桥塔顶预抬值为69 mm;南沙大桥坭洲水道桥预抬值为90 mm;深中通道伶仃洋大桥预抬值为100 mm[10]。

通过对于郭家沱长江大桥南北塔的桥塔预抬高值计算,在施工中给出的桥塔预抬高值为65 mm。为分析桥塔预抬高值对主缆空缆线形的影响,笔者拟采取南北桥塔均预抬高10、30、50、70、90 mm这5个工况对主缆空缆线形影响进行分析,计算结果采用相对桥塔预抬高值为50 mm的变化值表示,见表2。

表2 桥塔预抬值对主缆空缆线形影响

从表2可知:桥塔塔高变化与主缆空缆线形变化成正向关系,且基本呈线性变化规律。南北侧边跨跨中空缆矢高变化值基本相等,在桥塔预抬值为90 mm时,中跨跨中主缆矢高变化相对值达94 mm,影响较大,为确保主缆线形与设计线形一致,需在施工过程中严格控制桥塔高程精度。

2.3 弹性模量对主缆状态的影响

本桥主缆由133股、127丝、直径为5.45 mm的高强平行钢丝组成,钢丝弹性模量为1.97×105MPa。主缆钢丝在制作时会存在一定的弹性模量误差(-0.1×105～+0.1×105MPa),且钢丝弹性模量具有一定离散性,故其真实值也会有一定的变化范围,这将会影响主缆的索股实际长度。为分析不同钢丝弹性模量值对主缆空缆线形、索股无应力长度和主缆成桥内力影响,笔者分别取主缆钢丝弹性模量为1.87×105、1.92×105、1.97×105、2.02×105、2.07×105MPa进行有限元计算分析。计算结果采用相对设计基准弹性模量(1.97×105MPa)的变化值表示。图3为弹性模量对空缆线形影响;图4为弹性模量对主缆无应力长度影响;图5为弹性模量对主缆成桥内力的影响(采用绝对值)。

图3 弹性模量对空缆线形影响

图4 弹性模量对索股无应力长度影响

图5 弹性模量对主缆成桥内力影响

由图3可知:当钢丝弹性模量为2.07×105MPa时,主缆空缆线形的中跨跨中矢高降低了32.2 cm,边跨跨中矢高降低了3.8 cm,随着钢丝弹性模量增加,空缆线形的矢高将逐渐降低,且中跨跨中矢高变化值较南北两侧边跨大,呈现反向线性变化规律。总体来说,钢丝弹性模量对主缆线形影响较大。

由图4可知:弹性模量与索股无应力长度近似呈正向线性变化,当钢丝弹性模量取值为2.07×105MPa时,主缆索股的无应力长度增加了19.7 cm,影响较大。在进行主缆空缆线形计算时,施工控制目标是使主缆成桥状态能达到设计线形,即控制成桥主缆的等效曲线长度与设计长度一致。而主缆各跨的等效曲线长度Sc等于其索股无应力长度Sw与索股弹性伸长量Se之和,如式(2)。

Sc=Sw+Se

(2)

当Sc一定时,当钢丝弹性模量越大时,主缆弹性总伸长量越小,所对应的索股无应力总长度越长,由此计算得出的空缆跨中矢高越低。

由图5可知:弹性模量对成桥主缆内力影响较小,当弹性模量增加2.5%时,主缆水平张力仅增加2 kN(0.000 9%);竖向张力仅增加1 kN(0.001%)。

2.4 钢丝直径对主缆线形的影响

文献[11]指出:公称直径5.00 mm的钢丝允许偏差为±0.06 mm。为分析主缆钢丝直径误差对于主缆状态影响,笔者考虑选取主缆钢丝直径分别为5.39、 5.41、 5.43、 5.45、 5.47、 5.49、 5.51 mm,计算结果采用相对设计标准值5.45 mm变化值表示,如图6。

图6 钢丝直径对空缆线形影响

由图6可知:当钢丝直径为5.51 mm时,中跨跨中空缆矢高降低了15.5 cm,影响较为明显;南北跨跨中矢高分别2.2、1.6 cm,影响较跨中小。由此可知钢丝直径越大,空缆线形矢高越低,两者基本呈反向线性关系。

2.5 钢桁梁重量误差对主缆状态的影响

桥梁钢桁梁采用倒梯形断面形式,桁宽17 m;钢梁全长862.5 m,上层桥面主跨全宽39.0 m,边跨全宽37.0 m;主桁采用等高三角形桁式,标准节间长度15 m,标准节段重420 t;中部段长度20.5 m,钢材用量635 t。钢桁梁重量将直接影响主缆空缆线形、无应力长度和主缆成桥内力,由于钢桁梁重量在实际制造过程中存在着一定误差,本次采用每节段梁±2.5 t的误差进行计算分析。图7为钢桁梁重量误差对空缆线形影响;图8为钢桁梁重量误差对主缆无应力长度影响;图9为钢桁梁重量误差对主缆成桥内力的影响(采用绝对值)。

图7 钢桁梁重量误差对空缆线形影响

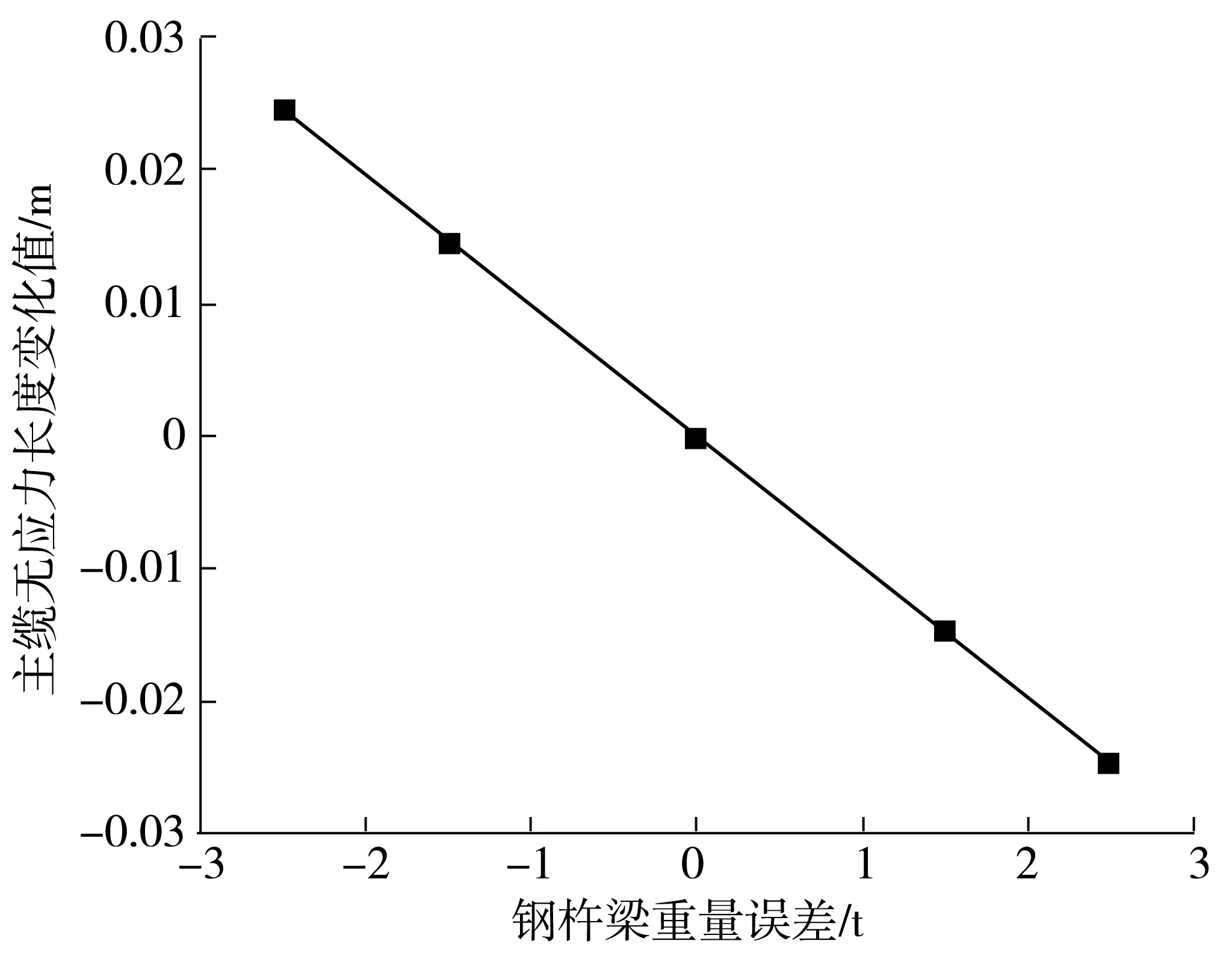
图8 钢桁梁重量误差对主缆无应力长度影响

图9 钢桁梁重量误差对主缆成桥内力影响

由图7可知:钢桁梁制造重量误差对中跨跨中空缆线形影响较大,当误差为+2.5 t时,主缆中跨跨中矢高将提高4.7 cm;对南北边跨跨中空缆线形影响较小,当误差为+2.5 t时,边跨跨中矢高仅提高0.7 cm。由此可看出两者基本呈现线性正向变化规律。

由图8可知:钢桁梁制造重量误差对主缆无应力长度影响较小,当误差为+2.5 t时,索股无应力长度减少2.5 cm。由此可看出两者基本呈现线性反向变化规律。

由图9可知:钢桁梁制造重量误差对主缆成桥内力有一定影响,当误差为+2.5 t时,成桥状态主缆水平张力增加了1 350 kN,成桥状态主缆竖向张力增加了587 kN。由此可看出两者基本呈现线性正向变化规律。

总体而言,钢桁梁重量制造误差对于主缆中跨跨中空缆线形影响较大,对主缆施工完成后的吊索下料长度计算影响也较大[12]。在施工控制中需要准确掌握钢桁梁称重数据,及时进行主缆索股架设及吊索下料长度修正调整。

3 参数敏感性评估

根据架设时主缆温度、桥塔预抬值、钢丝弹性模量、钢丝直径、钢桁梁重量误差等5个参数对主缆状态的分析结论,对影响主缆状态的参数敏感性进行对比评估,如表3。

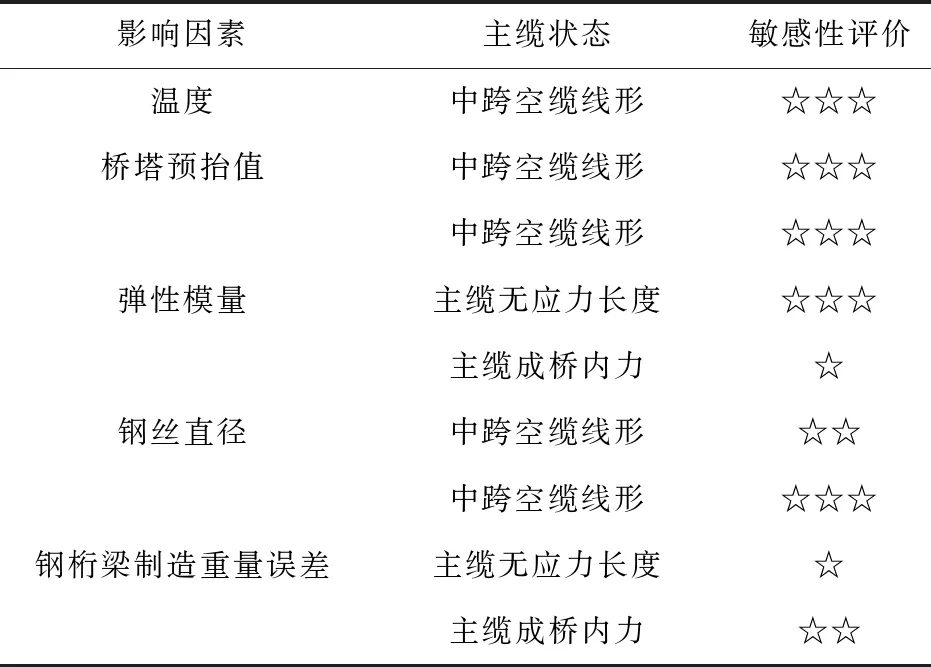
表3 主缆状态影响参数敏感性分析

4 结 论

1)温度是影响悬索桥结构受力的重要荷载,对空缆线形有着显著影响,属于高敏感性因素。在主缆架设施工过程中应对主缆温度场进行精确监测并将其反馈到调索计算工作中。

2)桥塔预抬值对空缆线形影响较大,两者基本呈正向线性变化规律,属于高敏感性因素。在施工过程中需严格控制塔顶高程精度。

3)主缆钢丝弹性模量对空缆线形、索股无应力长度影响较大,属于高敏感性因素。为准确计算空缆线形与索股无应力长度,在施工监控中应准确获取厂家生成的钢丝弹性模量实验值。主缆弹性模量对成桥主缆内力影响较小,属于低敏感性因素。

4)钢丝直径对空缆线形有一定影响,属于一般敏感因素。

5)钢桁梁重量误差对空缆线形影响较大,属高敏感性因素;对主缆无应力长度影响较小,属低敏感性因素;对成桥内力有一定影响,属一般敏感性因素。为确保架设精度,须在钢梁加工完成后,对其采取现场称重方式获得真实的重量并反馈到现场监控计算中。