光伏发电系统对配电网三相电压不平衡度影响的计算方法

陈 伟, 倪源宏, 纪青春, 王忠飞, 何 峰

(1. 兰州理工大学 电气工程与信息工程学院, 甘肃 兰州 730050; 2. 国网甘肃省电力公司 兰州供电公司, 甘肃 兰州 730050)

光伏随机出力和负荷分布不均是造成配电网三相电压不平衡的两个主要影响因素[1].传统的确定性评估方法因忽略了光伏和负荷的随机波动特性,在研究随机性因素对配电网不平衡度的影响方面存在缺陷[2].

目前,针对配电网电压不平衡度的研究主要集中在不平衡电网建模、不平衡机理分析、可接入光伏的极限值容量和治理优化策略等方面.Jayatunga等[3]提出了一种基于不平衡度因子的确定性方法,用来评估负载和线路对单相电压不平衡度的作用,然而确定性的方法只能分析随机变化量小或无变化的不平衡情况,通常是调整不同条件下的参数得到计算结果,且未考虑到光伏容量和波动的因素.Liu等[4]将蒙特卡洛模拟法运用到评估配电网不对称负载引起的电压不平衡现象,尤其重点分析了不平衡功率在各个线路上的传输问题.Miroshnyk等[5]基于持续时间的负荷图提出不对称电网电压计算方法,从而估计随机网络的不对称数值特征.Kong等[6]将三相不平衡功率分解为随机不平衡分量和系统不平衡分量,并提出新的先验判断方法,将系统不平衡分量按照不同场景计算不平衡度随时间的变化趋势,表明了负载变化对不平衡现象有着一定的影响.Navarro-Espinosa等[7]针对低压配电网不平衡现象提出概率评估方法,从而利用蒙特卡洛法分析了100个不同光伏渗透率与不平衡度之间的影响关系.Akbari等[8]继续深入研究分布式能源的影响效果,通过离散场景综合评估了光伏电源在接入位置、分散程度上对配电网三相电压不平衡度的影响,通过对比发现,接入位置越靠近公共连接点越集中,不平衡度越大.

基于以上分析,为了能对光伏发电系统的三相电压不平衡度进行准确评估,本文建立了以非参数自适应核密度估计法为基础的光伏出力和负荷模型,采用基于混合Copula函数的半不变量潮流法,并结合分段线性化方法减少非线性方程单点级数展开导致的误差增大问题,从而得到系统的运行数据,最后再通过重要抽样方法评估光伏出力和负荷波动对三相电压不平衡度的影响,仿真验证了本文方法的有效性和可行性.

1 光伏出力及负荷波动模型的概率分布

目前,大多文献对于光伏出力及负荷波动的建模采取Beta分布,但光伏出力在实际中并不一定严格遵循这种先验分布规律.非参数核密度估计法因不用基于大量历史数据而能进行分析,即不受函数的限制[9],故在对光伏出力和负荷波动拟合方面具有明显的优势.

当样本数据n足够大时,不同的核函数对估计结果没有太大影响,故采用高斯核函数[10].基于非参数核密度估计的光伏概率模型为

(1)

其中:n为实际测量得到的光伏数据样本数;h为带宽;Xi(i=1,2,…,n)为光伏出力实际数据.

为修改二阶及以上的模型估计边界偏差,采用伪数据法来适应普通数据的反射能力,其表达式为

(2)

其中:m为比nh大但比n小的整数.

传统非参数核密度估计法中求解带宽是以全部样本总误差和最小为目标求取的固定值[11],但无法保证估计结果的准确性和平滑性.

本文基于交叉验证法采取通过计算最小积分平方误差来求取最优带宽hb.最小积分平方误差表达式为

其中:fn(x)为采取固定带宽下的核密度估计值,则得到的最优带宽为

hb=arg min(f1n-f2n)

(5)

将式(5)代入式(2)中,可得光伏出力和负荷功率概率分布模型为

(6)

2 基于混合Copula理论的半不变量法潮流计算

2.1 Copula函数理论

使用半不变量潮流法的前提之一是输入量应相互独立,当输入量的边缘分布不满足这个要求时,对于联合分布的描述将变得十分困难.当已知多个边缘分布的随机变量时,Copula函数的显著特征是相关性在变换过程中能够保持不变.假设X1,X2,…,XN是N个随机变量,它们各自对应的边缘分布分别为F1(x1),F2(x2),…,FN(xN),它们的联合分布为H(x1,x2,…,xN),则存在一个能够将各变量的边缘分布和联合分布联系起来的函数C(·),使得下式成立:

(7)

(8)

选取适当的Copula函数极为重要.Luo等[12]提出了Pair Copula函数,赵渊等[13]提出了R藤Copula函数,但这些函数以及常规Copula函数在内的任意一种函数,因其对于尾部特性描述各不相同,故对变量之间的相关性表达存在差异.本文选择将Gumbel-Copula分布函数、Clayton-Copula分布函数和Frank-Copula分布函数结合为一种具备上下尾部特性的混合阿基米德Copula函数,即M-Copula函数,以便能清晰描述随机变量之间复杂的相关性关系[14],其公式为

(9)

其中:Ci(•)(i=1,2,3)分别代表Gumbel-Copula函数、Clayton-Copula函数和Frank-Copula函数;θi分别代表各函数的参数;ωi分别代表各函数的权重因子,且ω1+ω2+ω3=1,其数值利用备选Copula函数和经验Copula函数之间的最短欧式距离确定.经验Copula函数表达式为

(10)

其中:I[•]为示性函数,若[]内的条件满足则等于1,不满足则等于0.

欧式距离为:

(11)

通过求解式(11),可得ω1=0.251 4,ω2=0.238 7,ω3=0.509 9.

2.1.1未知参数的求取

利用期望最大化方法进行参数估计,将式(9)中的u用分布函数代替,可改写为

(12)

假设yi=(ui,vi)表示一个观测样本,引入一个隐藏变量zi=(zi1,zi2,zi3)后,该观测样本表示为xi=(yi,zi),令ψ=(ω,θ),则xi的条件概率可表示为

(13)

而整个观测样本X的条件概率可以表示为

(14)

为了找到整个观测样本的合适参数,对其求取对数似然函数期望,即:

(15)

其中:k为迭代次数.求得条件期望的最大值后,可以将所求参数表示为

ψ(k+1)=arg maxE(lnP(X|ψ(k)))

(16)

2.1.2相关性分析

利用Kendall秩相关系数τ[15]来计及相关性,可表明变量变化相同和不同的概率.设随机变量X、Y的累积分布函数为F(X)和G(Y),其数据来自于随机变量的样本(X,Y),并令Copula函数为C[F(X),G(Y)]:

τ(X,Y)=4×

(17)

2.2 半不变量法潮流计算

2.2.1系统分段线性化潮流方程

将功率和电压方程用极坐标的矩阵形式表示,并引入泰勒级数在基准运行点处展开,忽略掉2次及以上的高阶项,可得:

(18)

将式(18)移项可变换为

ΔX=S0ΔW, ΔZ=T0ΔW

(19)

当系统处于正常运行状态时,可通过稳态潮流算法求取基准运行点得到X0、Z0和J0,从而再求取S0和T0.当已知节点注入功率扰动ΔW后,可根据式(19)求取ΔX和ΔZ.

系统中的随机扰动ΔW由光伏注入功率ΔWpv和负荷吸收功率ΔWL构成,表达式为

ΔW=ΔWpv⊗ΔWL

(20)

其中:⊗代表卷积运算.

利用半不变量可加性,式(20)可改写为

(21)

联立式 (19～21)求得各节点状态变量ΔX和各支路功率变化量ΔZ的各阶半不变量:

(22)

当光伏渗透率过高时,必然引起节点注入量波动过大,这使得传统半不变量法容易产生较大的截断误差[16].所以为使节点电压计算结果更为准确,提出分段线性化的方法.

1) 把节点分为光伏接入点和非接入点,分别标记为j和1、2、…、j-1、j+1、…、n.对于接入点,注入功率Sj可划分为m段,即:Sj0～Sj1、Sj1～Sj2、…、Sjm-1～Sjm,并设每段期望值为Ej1、Ej2、…、Ejm;对于非接入点,每段期望值为E1、E2、…、Ej-1、Ej+1、En.

3) 对于状态量的半不变量值可采用文献[17]的方法进行求解,再利用下文的级数展开方法求取ΔX和ΔZ的近似随机分布.

2.2.2级数展开

Cornish-Fisher级数展开法因其密度函数不会出现负值从而具有较好的尾部收敛特性,其计算精度不会受随机输入变量的影响[18-19].假设输出变量z的分位数为α,则z(α)可表示为

(23)

其中:ζ(α)为标准正态分布CDF的反函数,即满足ζ(α)=Φ-1(α);gn为z的n阶半不变量.根据z(α)=F—1(α)即可求得输出变量z的累积分布函数F(z),再对F(z)求导可获得z的概率密度函数f(z).

2.3 不平衡度抽样计算步骤

通过求取节点电压值实现对三相电压不平衡度进行评估[20],具体流程如图1所示.

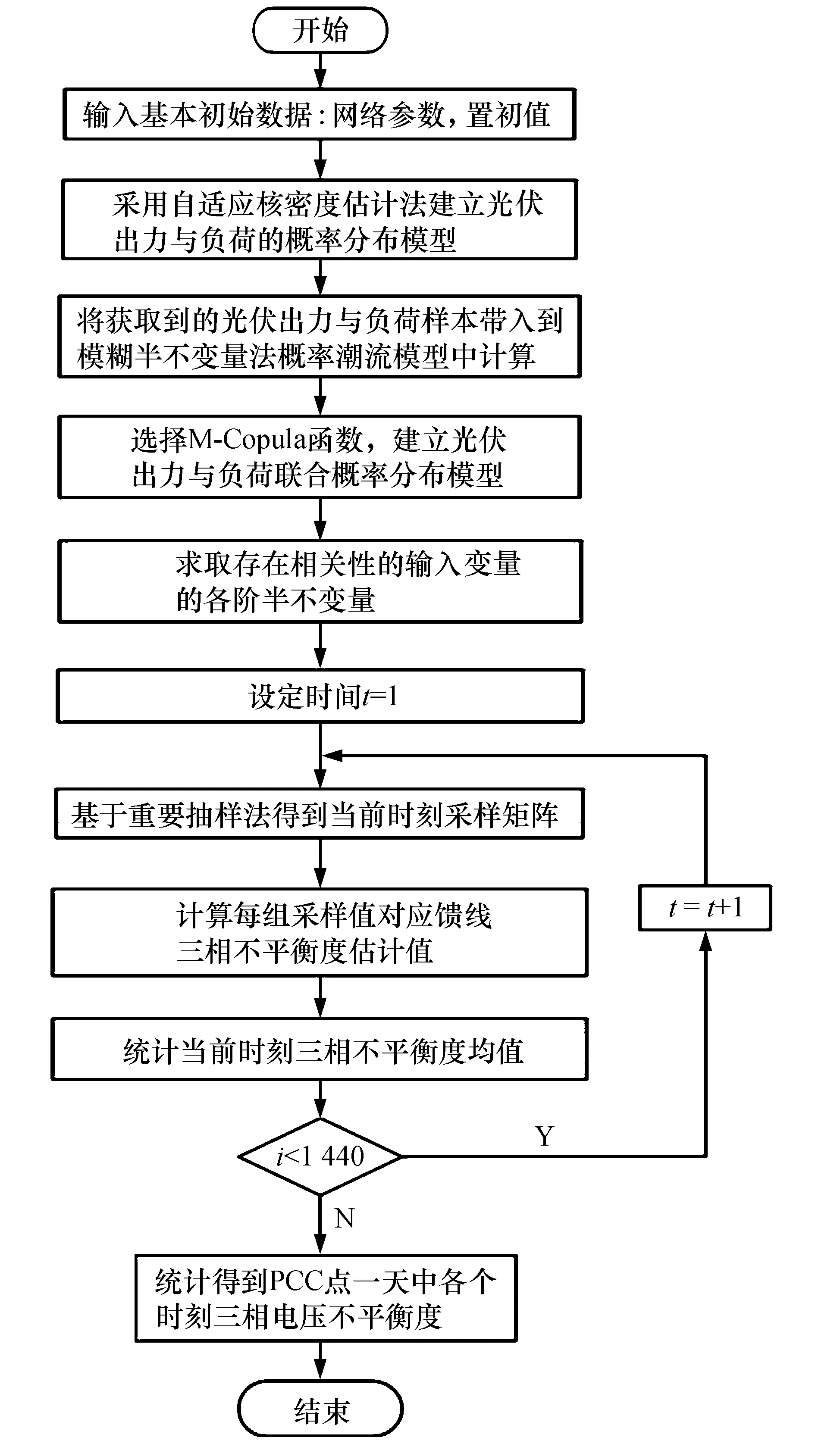
图1 分段线性化半不变量计算流程图

3 算例分析

3.1 对光伏出力和负荷功率的建模分析

以西北某光伏发电场出力和当地负荷的实测数据为样本,样本数n为1 000,采样间隔时间1 min,通过第1节所述方法得到了基于非参数自适应核密度估计法的概率密度曲线,与普通核密度估计进行对比,结果如图2和图3所示,其中图3描述了某一节点负荷的模型.

图2 不同方法下的光伏出力概率密度对比

图3 不同方法下的负荷功率概率密度对比

χ2检查是评价拟合程度的常用方法,是通过判断理论频数与实际频数的差值所得.由表1可知,通过χ2结果是否通过检查来对比所采用方法的优劣程度,证明了本文所提方法能够较好拟合光伏出力和负荷功率数据.由图2和图3可得知,以样本数据为参照,通过比较发现传统的核密度估计只能表达出光伏波动和负荷功率的变化趋势,并不能够准确描述其情况,这是因为采用了固定带宽的方法,所以存在较大误差.具体表现在:图2的3～5 MW和12～15 MW、图3的1.5～1.7 MW和2.0～2.4 MW阶段中,波峰和波谷的误差较大,会影响后续三相电压不平衡度计算.而非参数自适应核密度估计能够较好地对光伏出力和负荷功率进行跟踪拟合,是因为这种方法根据不同的数据密度选取不同的带宽长度从而适应了局部特性.

表1 改进前后的评价指标

3.2 三相电压不平衡度的计算方法

根据GB/T 15543-2008《电能质量 三相电压不平衡》,三相电压不平衡度计算公式为

(24)

其中:U1为正序电压分量;U2为负序电压分量.

3.3 对三相电压不平衡度的建模分析

选取了IEEE33节点进行仿真验算,如图4所示.该系统的基准电压为12.5 kV,基准容量为10 MV·A,在9和11节点接入光伏电源并通过调整光伏容量来改变渗透率的大小,其他节点分相接入3.1节所述的负荷模型.设定节点24为公共连接点,其一天之内平均三相电压分别为12.948、12.382、11.127 kV.标准规定,电网正常运行时,公共连接点电压不平衡度不超过2%,日累积大于2%的时间不超过72 min(指标1),且每30 min中大于2%的时间不超过5 min(指标2).以这2种指标为准对三相不平衡度进行评估,可分为2个部分:(1) 负荷波动对三相不平衡的影响;(2) 光伏容量对三相不平衡的影响.

图4 IEEE33节点配电系统

3.3.1负荷波动对三相不平衡的影响

针对分相接入的负荷波动情况,一天之内公共连接点的负荷功率波动最大值为23.37 MW,最小值为6.45 MW.由图5和图6可看出,三相不平衡度每日有98.293%的概率不超过72 min,每30 min仅有45.626%的概率不超过5 min.虽已接近标准1的规定,但是该情况下的三相不平衡度仍然有52.374%的概率不满足标准2,对这种现象,需要采取治理方案加以控制.

图5 日累计超标时间累积分布概率

图6 每30 min内超标时间累积分布概率

3.3.2光伏容量对三相不平衡的影响

选择节点9和11作为光伏的接入点,根据光伏渗透率的公式,可通过改变光伏容量实现光伏渗透率的不断增大.

通过仿真统计可得到一天之内三相不平衡度超标概率,如图7所示.

图7 一天之内三相不平衡度变化曲线

由图7可看出,在一天之内三相不平衡多集中于11～14时,尤以12时前后最为严重,这是因为这些时间段辐照度变化较大且为用电高峰期,增加了不平衡的超标概率.

如图8所示,随着光伏渗透率的增大,三相不平衡度的合格概率逐渐减小,通过比较发现,当渗透率不高的时候,三相不平衡度受到的影响较小,而当渗透率过高的时候,三相不平衡度受到的影响较大.尤其可以从图9看出,当渗透率达到35%的时候,系统的三相不平衡度将有极大概率超过标准1所规定的72 min,当渗透率达到50%的时候,不符合国家标准规定:日累积不平衡度大于2%的时间不超过72 min.

图8 不同渗透率下的三相不平衡度累积概率曲线

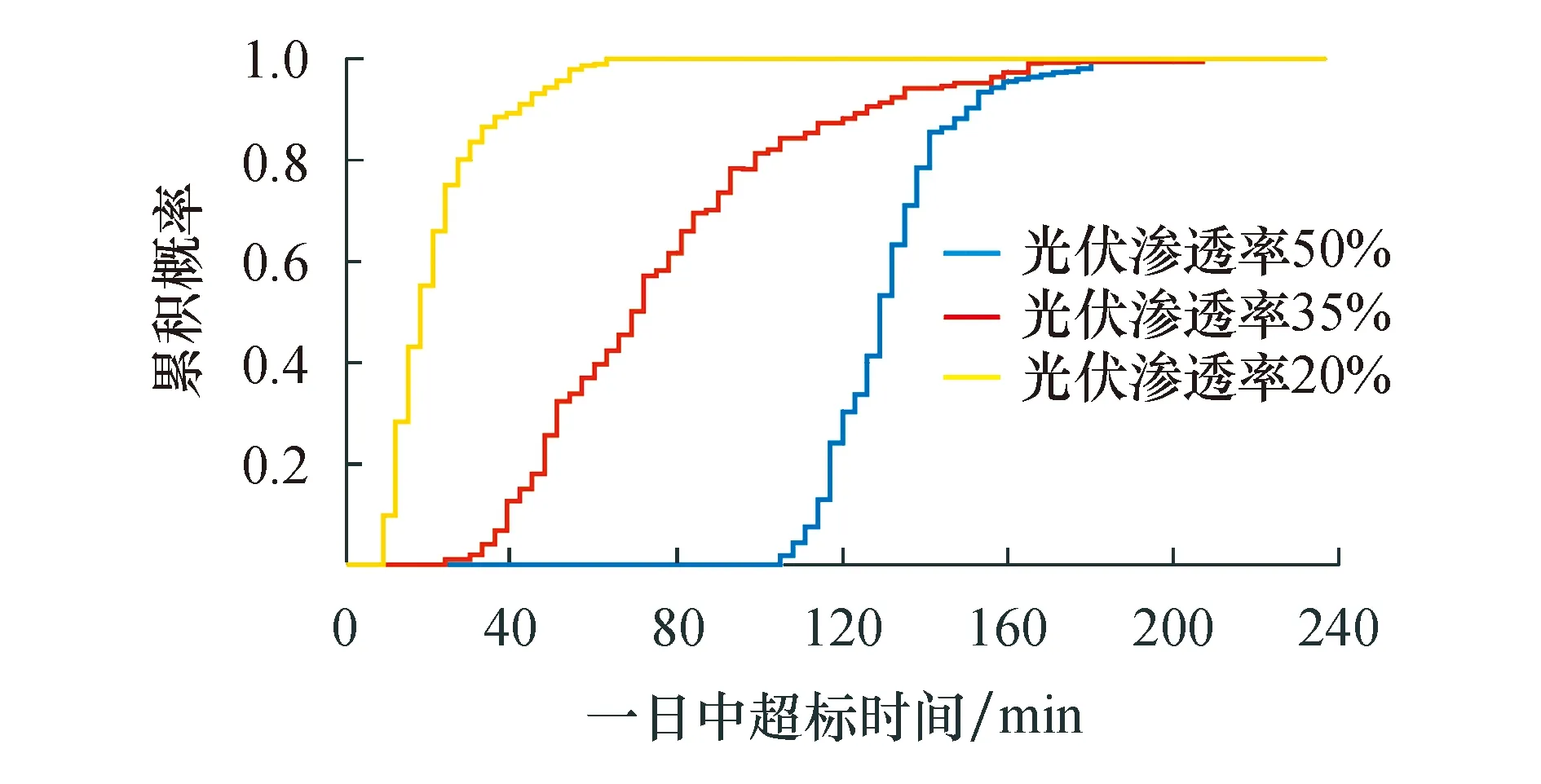
图9 不同渗透率下的一日内超标时间累积概率

4 结论

为了分析光伏出力和负荷波动对电网三相电压不平衡度的影响情况,本文提出了一种基于M-Copula的半不潮流的计算评估方法.仿真实验结果表明:

1) 利用非参数自适应核密度估计法对光伏出力和负荷波动进行描述,因为采取了带宽跟踪的方法,所得到的模型比传统核密度估计方法更为准确.

2) 利用分段线性化的级数展开方法,可以减小半不变量潮流计算中的误差,其中的基本矩阵能够更好地反映出节点电压变化情况.

3) 通过节点电压数据抽样计算得到不平衡度变化曲线,可发现光伏出力和负荷波动对三相不平衡度都产生了相应的影响.随着光伏渗透率的不断增加,不平衡度超标概率将迅速增大,当渗透率达到一定值时,三相电压不平衡度会超出国家标准,需加以补偿设备进行治理以恢复配电网三相电压不平衡度到允许范围内.

致谢:本文得到国网甘肃省电力公司科技项目(SGGSLZ00FCJS2000712)的资助,在此表示感谢.