滑坡碎屑流作用下埋地管道轴向应变特性

王 辉, 胡海涛, 谢 越, 麻宏强*,4

(1. 甘肃建投河西建设管理有限公司, 甘肃 武威 733000; 2. 甘肃建投科技研发有限公司, 甘肃 兰州 730050; 3. 华东交通大学 土木建筑学院, 江西 南昌 330013; 4. 兰州理工大学 土木工程学院, 甘肃 兰州 730050)

我国是地质灾害时常发生的国家,常有地动、地面塌陷、滑坡、坍塌等地质灾难频繁发生.滑坡泥石流和坍塌等灾难对于天然气集输管道的影响极为严重,易造成管道大变形及断裂等失效形式,从而导致油气管道泄漏,管线停输和环境污染,更严重者将造成爆炸,对人员的安全造成严重的威胁,并且给当地造成巨大经济损失[1-2].其中,滑坡灾害是导致管道失效的主要风险之一,针对长期输送石油和天然气的管路来说,在滑坡灾难时常发生的地区,特别易造成管路的变形和损坏,更加严峻的情况是造成天然气和石油的泄漏等安全问题[3-4].

滑坡-碎屑流是滑坡的一种类型,具有爆发频次高、分布领域广等特点[5-6].滑坡-碎屑流爆发时,会造成河道堵塞,破坏丛林和耕地,导致重大的经济和人员损失,给自然环境造成巨大的破坏[7-8].当前,滑坡碎屑流区域埋地管路灾害风险的研究把穿过滑坡区域管路的变形和位移、应变力分布、以及其他因素对管路变形和应变的影响规律作为重要研究对象[9-11].车福利[12],刘慧[13],梁政[14],张东臣[15],郑光[16]建立纵向、横向、斜向穿越滑坡体的管土模型,就滑坡碎屑流区域埋地管路灾变影响进行了相关研究,但基本是针对穿越滑坡体管道展开,未见滑坡碎屑流作用条件下埋地管道轴向应变特征以及影响规律的相关研究.而在碎屑流作用下,埋地管路位移、应力应变受管道结构参数、运行参数等多种因素影响,且各类影响因素的影响规律可能存在较大差异[17-19].所以为了更好地掌握碎屑流作用下埋地管路应变力的影响规律,需要对各个因素逐个展开分析.同时,为了给滑坡区埋地集输管道灾变风险研究提供理论基础,也需要对碎屑流作用下的埋地管路应力和变形分布特征和影响规律进一步研究.

本文基于热-弹塑性理论,采用管-土耦合方法,创建了碎屑流纵向作用下埋地管路应力和变形分析模型,对不同滑坡碎屑流长度、宽度和厚度条件下埋地管道轴向应变规律进行研究,分析了管道径厚比、管壁减薄和管道埋深等结构参数对轴向拉伸应变的影响规律,并综合探讨了各结构参数对轴向拉伸应变的敏感性.

1 碎屑流作用下埋地管道应变模型建立

1.1 埋地管道应变模型的建立

建立滑坡碎屑流作用条件下的埋地管道应变分析模型,是埋地管道应变规律研究的基础.滑坡碎屑流与管道模型作用机理较为复杂,有必要将其合理简化.基于弹塑性力学理论,本文采用有限元方法,创建碎屑流作用下的埋地管路应力和变形的分析模型,并对埋地管道应变模型网格进行无关性验证.

小型滑坡碎屑流在土壤表面滑动的过程中,其堆积形态类似于半椭球体,在土壤表层作用示意图如图1所示.所以在本文中,可以把地表滑坡碎屑流发生流程中的堆集状态大致视为半椭球体状.同时,根据碎屑流颗粒流相关理论,碎屑流运动是其贴近地面侧的剪切力以及碎屑流本身所具有的重力一起作用造成的结果,因此碎屑流针对埋地管路最上层土壤外表面所产生的作用,可以将其同等为它针对土壤外表面的压力以及摩擦力所产生的作用.所以碎屑流针对埋地管路最上层土壤外表面的作用力可以根据下列等式来计算.

图1 小型滑坡碎屑流作用示意图

(1)

式中:a、b、c为埋地管路最上层土壤外表面碎屑流的长、宽、高;g为重力加速度,g=9.8 m/s2;ρ为碎屑流的密度;θ为水平面与坡面的夹角;η为土壤外表面同碎屑流之间的摩擦系数,根据岩土勘查工程的相关手册取其值为0.3.

为了方便本文相关内容的分析,本文在沿着管路长度的方向上取65 m,沿着管路两边取宽度30 m的管道和土壤范围区域,用以研究埋地管路的变形;同时,为了进一步缩小埋地管路最下层土壤给通过模拟得到的结果造成的相关影响,通过许多估计和计算确定其值取6.2 m,图2为通过简化处理后的碎屑流作用条件下埋地管路应变模型.

图2 通过简化处理后的碎屑流作用下埋地管路应变模型

1.2 模型边界条件

碎屑流作用条件下,埋地管路产生变形是埋地管路运行压力、温度及土体共同造成的结果.因此,如果需要对碎屑流作用条件下埋地管路变形进一步研究,则须增加适合的边界条件.依据实际条件,本文在埋地管道两端的截面,即y=0 m和65 m两截面,施加管长方向固定约束边界,模拟远离滑坡碎屑流区域管土的稳定状态;在埋地管道两侧,即x=±15 m两截面,采用x方向固定约束边界,模拟远离滑坡碎屑流区域土体稳定状态;在土壤底层,即z=-7 m截面,采用全自由度固定约束,模拟底层土壤稳定.同时,为模拟天然气运行参数对埋地集输管道的影响,在管道内壁施加温度和压力边界.

1.3 网格划分及无关性验证

上述模型的网格划分运用了结构化网格来进行,并且针对模型所划分的网格进行了相应的无关性验证.选取四套节点数分别为270 000、460 000、660 000和800 000的网格,对同一工况的计算结果进行对比,当网格的节点数超过270 000的时候,节点数对于计算结果所产生的影响相对比较小.根据结果来斟酌计算效率受到节点数的影响,最后确定采用网络节点数270 000时的网格来模拟验证并进行相关分析.

同时,对普光实验管道进行应变监测,即采用管道外壁面的应变传感器实时测量管道壁面应变来反映整条管线应变风险,其应变片安装如图3所示.针对模型,选取管路埋深H=0.8 m,坡度角θ=π/9,天然气温度T=328 K,压力P=8.9 MPa条件下,利用普光气田监测的相关数据来验证其可靠性.由于在监测时,滑坡碎屑流没有发生,所以在验证模型的时候,取Fy、Fz都是零的时候,模拟分析了实际运行过程中压力和温度波动对管道应变的影响,并针对模型y=25 m的截面,比较通过监测所得值同实际管路轴向应变值之间的异同.表1是埋地天然气集输管道轴向应变监测值与模拟值对比结果.结果表明,通过数值模拟得到的结果和通过监测所得的应变值之间误差稳定10%内,这说明通过数值模拟取得的结果是可靠的.

图3 普光实验管道的应变片安装示意图

表1 埋地天然气集输管道轴向应变监测值与模拟值对比(y=25 m)

2 碎屑流作用下埋地管道轴向应变分布特征

滑坡碎屑流作用条件下,管道轴向拉压应变远远大于环向拉压应变,因此管道应变风险应主要考虑轴向拉压应变,以保证管道安全运行.基于滑坡碎屑流作用条件下的埋地管道应变分析模型,本文针对不同滑坡碎屑流长度、宽度和厚度条件下埋地管道轴向应变分布特征进行研究.

图4是埋深取0.8 m、运行压力取8.9 MPa、天然气温度取328 K、山体坡度取π/9时,不同长度的滑坡作用条件下,323.9/14.2管道轴向应变分布规律.由图4可知,滑坡碎屑流长度与管道轴向应变分布息息相关,不同长度的碎屑流作用条件下,管道轴向应变分布不尽相同.沿着滑坡方向,左侧管道轴向应变主要为拉应变,右侧管道为压应变,对应的左侧管道主要受拉力作用,右侧管道受压力作用.同时,随着滑坡长度的增加,管道轴向应变作用范围也随之增加,分布形态由原先的纺锥形沿滑动方向伸长,沿水平轴向上下扩大.

图4 不同滑坡长度条件下管道轴向应变分布(TH=1,W=5,D/t=323.9/14.2)

图5是埋深取0.8 m、运行压力取8.9 MPa、天然气温度取328 K、山体坡度取π/9时,不同宽度的滑坡作用条件下,323.9/14.2管道轴向应变分布规律.由图5可知,不同宽度的碎屑流作用条件下,管道轴向应变分布也不尽相同.沿着滑坡方向,左侧管道轴向应变主要为拉应变,右侧管道为压应变,对应的左侧管道主要受拉力作用,右侧管道受压力作用.同时,当滑坡碎屑流宽度增加时,分布形态变化主要以在滑坡碎屑流影响区进行上下扩展.

图5 不同滑坡宽度条件下管道轴向应变分布(L=5,TH=1,D/t=323.9/14.2)

图6是埋深取0.8 m、运行压力取8.9 MPa、天然气温度取328 K、山体坡度取π/9时,不同厚度的滑坡作用条件下,323.9/14.2管道轴向应变分布规律.由图6可知,不同厚度的碎屑流作用下,管道轴向应变分布也不尽相同.随着碎屑流厚度的不断增加,分布形态变化主要以在滑坡碎屑流影响区进行上下扩展,并且通过对比图4和图5可知,滑坡碎屑流对管道轴向拉压应变的影响程度从大到小依次为滑坡厚度、长度、宽度;同时,通过比较不同滑坡尺寸条件下的管道轴向应变分布图,也可以发现滑坡碎屑流影响范围大致为滑坡区域的2到3倍左右.

3 结构参数对管道最大轴向拉压应变影响规律

滑坡碎屑流作用条件下的埋地管道受多种因素影响,除管土力学性能外,还可能受管道温度、压力等运行参数,滑坡碎屑流的长、宽、厚等结构尺寸,管道的管径和壁厚等结构尺寸,以及管道埋深、敷设坡度等因素的影响.本文就管道径厚比、管壁减薄和管道埋深对管道的轴向拉压应变影响规律进一步分析.

3.1 径厚比对管道轴向拉压应变的影响规律

图7是埋深取0.8 m、运行压力取8.9 MPa、天然气温度取328K、山体坡度取π/9、碎屑流的长度和厚度分别取5 m和2 m时,管路轴向最大拉压应变随着管路径厚比发生改变而改变的规律.由图7可知,轴向最大拉压应变的变化趋势基本一致,其会随管路的径厚比增长而先减小后增加,往往管道轴向最大拉应变稍微大于轴向最大压应变,若是较大规格管道,其拉压最大应变差异更大.结合CSA管道应变失效评价方法,拉压极限应变一致时,滑坡碎屑流作用条件下,使用拉伸应变进行管道风险评价时,采用较大规格管道得到的结果偏于保守,但也更为安全.因此,径厚比对管道轴向拉压应变的影响较小.

图7 管路轴向最大拉压应变随着管路径厚比发生改变而改变的规律(L=5、W=5、TH=2)

3.2 管壁减薄对管道轴向拉压应变的影响规律

图8是埋深取0.8 m、运行压力取8.9 MPa、天然气温度取328 K、山体坡度取π/9、碎屑流的长、厚以及宽分别取5、2、5 m时,323.3/14.2管路轴向最大拉压应变随着管壁面厚度均匀减薄而改变的规律.由图8可知,管道轴向最大拉应变随管壁面厚度均匀减薄成指数形式快速增加;压应变先迅速增加,而当壁厚减薄大于40%后,压应变基本保持不变.

图8 管路轴向最大拉压应变随着管壁面厚度减薄而改变的规律(L=5、W=5、TH=2)

3.3 管道埋深对管道轴向拉压应变的影响规律

图9是埋深取0.8 m、运行压力取8.9 MPa、天然气温度取328 K、山体坡度取π/9、碎屑流的长、厚以及宽分别取5、1、5 m的时候,管路轴向最大拉压应变随着管路埋深发生改变而改变的规律.根据图9可以看出,轴向最大拉压应变随着埋土深度的不断增加,拉压应变随之明显减小.这说明铺设在坡度较小的边坡的管道,在滑坡碎屑流作用下更容易受损,应加强此类边坡防护.由于管路轴向拉压应变随管路不断增加的埋深厚度而显著减小,那么对于滑坡碎屑流多发区域,应适当地增厚管路的埋深才可以减小滑坡碎屑流灾害威胁.

图9 管路轴向最大拉压应变随着管路埋深发生改变而改变的规律(L=5、W=5、TH=2)

4 敏感性分析

为了更好地研究管道结构参数对管道最大轴向拉压应变的敏感性,将通过式(2)对其结构参数进行归一化处理,即将原始数据经下列公式计算后得到新数据,进而比较管道结构参数对管道最大轴向拉压应变的影响程度:

(2)

式中:Xnorm为通过归一化的方法整理之后得到的数据;X为需要进行敏感性分析的原始数据;Xmax为所有进行敏感性分析的原始数据中最大的X值;Xmin为所有进行敏感性分析的原始数据中最小的X值.

图10为管道结构参数对管道最大轴向拉压应变的敏感性.结果表明,管道的壁厚减薄与管道轴向拉压应变呈正相关,管道埋深与之呈负相关.其中,随管路向下埋深的厚度不断地增加,滑坡碎屑流作用下管道最大轴向拉压应变分别减少了41%和55%.而随着管道壁厚从0减少至60%,滑坡碎屑流作用下管道最大轴向拉压应变分别增加了39%和23%.但随着管路径厚比的不断增长,管道轴向拉压应变基本保持不变.显然,管道的径厚比针对管道最大轴向拉压应变的影响并不大,可以忽略不计.而管道的壁厚减薄和管道埋深是影响其最大轴向拉压应变的主要因素.从管道结构参数对管道最大轴向拉压应变影响的影响程度来看,依次为管道埋深、管壁减薄、径厚比.在滑坡碎屑流灾害作用条件下,低坡山体埋设的管线风险相对更大.因此,适当增加滑坡碎屑流作用条件下的管道埋深可以减小滑坡碎屑流灾害作用风险.

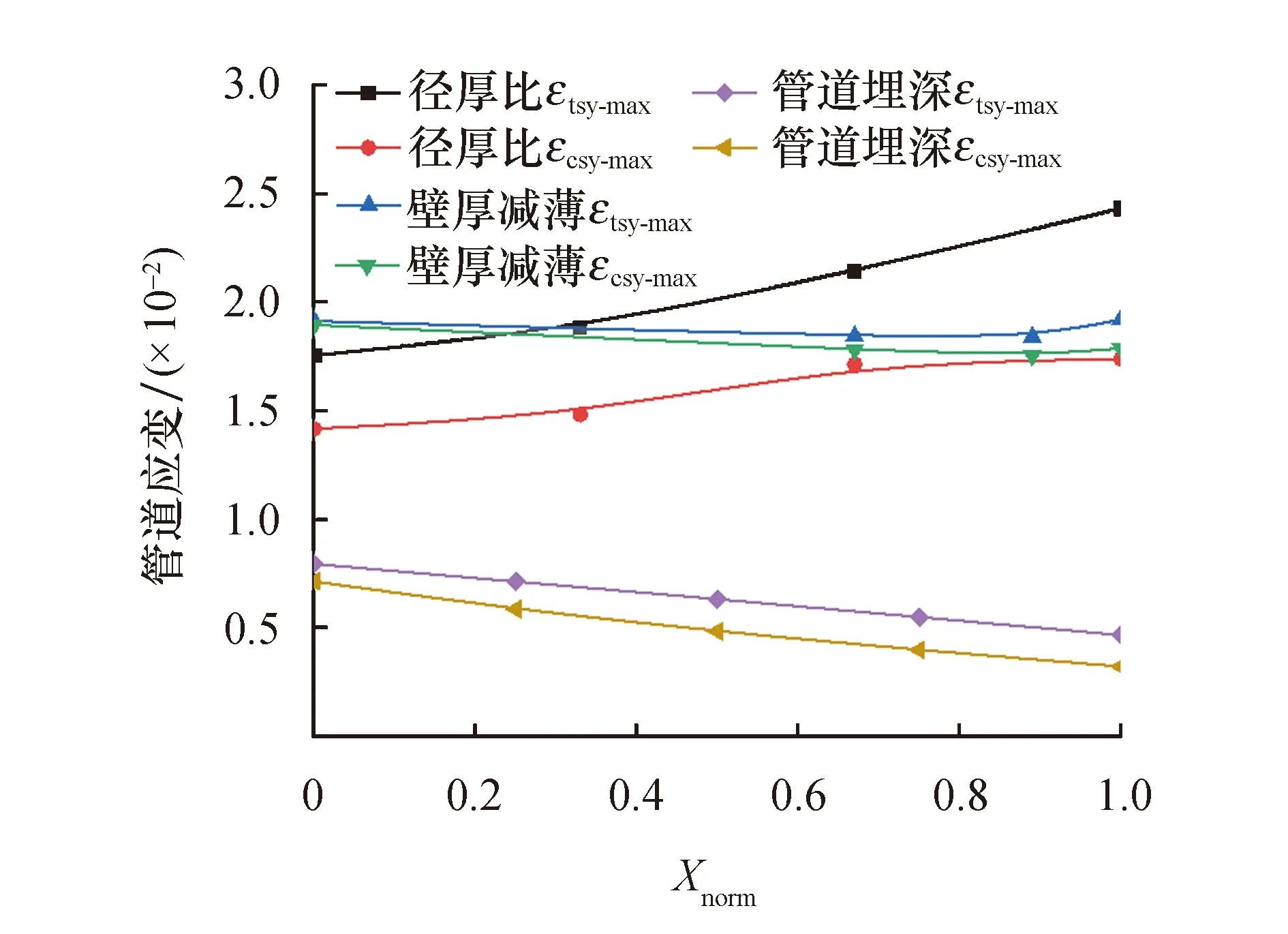
图10 管道结构参数对管道最大轴向拉压应变的敏感性

5 结论

本文根据热-弹塑性理论,利用管-土耦合的方法,创建了滑坡碎屑纵向作用条件下埋地管路的应变分析模型,并以此为基础对埋地管路的轴向拉压应变的分布规律进行了相关的研究分析,并在此基础上研究了管道结构参数对埋地管道轴向拉压应变的影响规律和各结构参数对轴向拉伸应变的敏感性,结论如下:

1) 管道的轴向最大拉压应变随滑坡碎屑流尺寸长、宽、厚的增加而增加.从滑坡碎屑流尺寸对管道轴向拉压应变的影响程度来看,从大到小依次为滑坡厚度、长度、宽度.比较不同滑坡尺寸条件下的管道轴向应变,滑坡碎屑流影响范围大致为滑坡区域的2到3倍左右.

2) 管道的轴向最大拉压应变随着埋土深度的不断增加而明显减小.这说明铺设在坡度较小的边坡的管道,在滑坡碎屑流作用下更容易受损,应加强此类边坡防护.由于管路轴向拉压应变随管路不断增加的埋深厚度而显著减小,那么对于滑坡碎屑流多发区域,应适当地增厚管路的埋深才可以减小滑坡碎屑流灾害威胁.

3) 管道的壁厚减薄和管道埋深是影响其最大轴向拉压应变的主要因素.从管道结构参数对管道最大轴向拉压应变的影响程度来看,依次为管道埋深、管壁减薄、径厚比.在滑坡碎屑流灾害作用条件下,低坡山体埋设的管线风险相对更大.因此,适当增加滑坡碎屑流作用条件下的管道埋深可以减小滑坡碎屑流灾害作用风险.