基于深度学习的火花放电等离子体反应器电压波形优化设计
尹 博, 朱益飞
(1.西安交通大学机械工程学院,西安,710049;2.空军工程大学航空动力系统与等离子体技术全国重点实验室,西安,710038)
近些年来,国内外大量学者针对非平衡等离子体在工业领域的应用开展了较多研究,大多数非平衡放电的应用依赖于高能电子驱动的化学性质。对于火花放电来说,其优势是高能量沉积和高化学活性,被广泛应用于点火助燃[1-2]、流动控制[3-5]、表面处理[6-7]、能源转化[8-9]、高压开关设计[10]等。等离子体点火助燃近年来受到了国际众多学者的广泛关注,其可以改善点火燃烧的一些关键领域,例如:可靠点火[11]、稳定燃烧[12]、熄灭[13]等。纳秒重频脉冲(NRP)火花放电与热等离子体不同,它不仅仅依靠局部高温维持燃烧,由放电产生的高能电子与中性分子碰撞而发生离解、激发和电离等反应,产生大量的活性粒子与燃料相互作用,促进燃料的裂解以增强点火和充分燃烧。传统的等离子体点火助燃反应器是基于重复性实验设计的,但随着飞行高度升高,气压降低和燃烧室流速增大,单纯的热效应会无法适应逐渐恶劣的环境,能量沉积、释放慢,加热速度低于流动速度会导致点火失败,严重限制了燃烧室的安全工作边界。为了维持火花放电,要更合理更高效地控制等离子体放电反应,产生所需的活性物质和能量,以纳秒为时间尺度调节电源电压波形实现活性物质和能量的优化设计。电源电压波形和频率是影响火花放电的关键参数,基于等离子体中的反应动力学过程和活性组分密度设计,机器学习的反向求导非常适合求解此逆问题,其计算代价和效率远低于传统实验调参。
近年来,机器学习已成功应用于众多领域,如计算机视觉[14]、语音识别[15]、自然语言处理[16]、自动驾驶[17]等。有专家学者在等离子体领域也开展了一些探索性研究。Kawaguchi等使用前馈神经网络求解电子速度分布函数的玻尔兹曼方程[18]。Zhong L L等利用深度神经网络代替传统模型求解热等离子体模型中的偏微分方程[19]。Mathews等证明了受偏微分方程约束的物理信息深度学习模型可以从压力信息数据中准确地学习与流体理论一致的湍流场[20]。Aguilar等利用传统粒子模拟方法计算的相空间信息和电场训练全连接神经网络和卷积神经网络,提出了一种基于粒子相空间信息的网格预测电场的新方法[21]。上述工作表明深度学习在等离子体领域已经开始慢慢崭露头角,但在等离子体反应动力学领域还鲜有研究。
本文在等离子体反应动力学的基础上,耦合深度学习模型,基于火花放电实验,利用二维流体模型计算分析放电过程,并与实验所测电流和光谱数据进行了对比验证;基于二维模型计算的电场,利用零维反应动力学模型进一步对点火助燃重要组分进行敏感性分析;最后利用深度学习模型基于组分密度逆向设计等离子体反应器的电源电压波形,为点火助燃提供所需的活性物质并降低能耗,此项工作为控制等离子体放电提供了新的思路和想法。
1 模型描述
本节简单介绍3个模型:零维等离子体动力学求解器-ZDPlaskin、二维并行流柱等离子体耦合求解器模型-PASSKEy和数据驱动模型-DeePlaskin。ZDPlaskin用来求解非平衡等离子体放电体系中组分密度随时间的演化[22]; PASSKEy用来求解非平衡等离子体中电场、组分密度和流体动力学的时空演化[23],且已在SDBD和针板放电中与实验(E-FISH)测量的电场进行对比验证[24];DeePlaskin耦合了全局等离子体模型和深度学习用来逆向求解非平衡等离子体中的一些关键参数,该模型已经与毛细管放电实验结果数据进行验证[25]。
1.1 等离子体化学反应动力学模型
ZDPlaskin是一个免费的Fortran程序用来计算组分密度和气体温度随时间的演化,它集成了BOLSIG+求解器[26]和QTPlaskin后处理程序,前者用来求解电子反应速率系数和电子能量分布函数,后者用来读取和查看输出结果。在ZDPlaskin模型中认为火花放电通道导通后放电区域呈均匀分布,即可通过零维模型描述整个放电区域的所有组分密度随时间的演化,且两电极之间的电场也可以表述为电压与电极间距比。对于组分密度的求解,ZDPlaskin的求解机理可以用式(1)描述:
(1)
式中:[Ni]是组分数密度;Qij是反应源项。式(1)是反应体系中组分i数密度。ZDPlaskin运用VODE求解器积分方程,将反应动力学化为求解常微分方程组。如果反应是电子碰撞反应,则反应速率系数通过耦合的BOLSIG+计算电子碰撞截面得到。
1.2 二维火花模型
PASSKEy通过求解电场的泊松方程、漂移-扩散反应方程和光电离的Helmholtz方程来计算等离子体中电场、组分密度和流体动力学的时空演化。在PASSKEy中泊松方程对整个计算域进行电场求解,如式(2)、(3)所示。
∇(ε0εr∇Φ)=-ρ-ρcδs
(2)
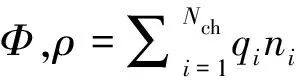
(3)
式中:ε0和εr分别为介电常数和相对介电常数;Φ为电势;E为电场;ρc为介质表面电荷;δs为Kroneckerδ函数;qi、ni分别为组分i的数密度和电荷;Nch为带电组分数目。
基于局域场近似的漂移-扩散方程如式(4)、(5)所示:
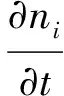
(4)
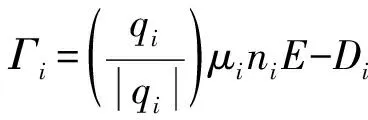
(5)
式中:Γi为通量;Si和Sph分别为反应源项和光电离源项;μi为迁移率;Di为扩散系数。基于局域能量近似把电子输运系数和反应速率系数表示为平均电子能量的函数。
光电离源项根据三指数Helmholtz光电离模型计算N2∶O2混合物放电[27],并基于测量的光电离函数给定了拟合参数。
1.3 DeePlaskin模型
DeePlaskin耦合了全局等离子体模型和深度学习模型来逆向求解非平衡等离子体中的一些关键参数,整体框架如图1所示,求解过程可以分为3步。
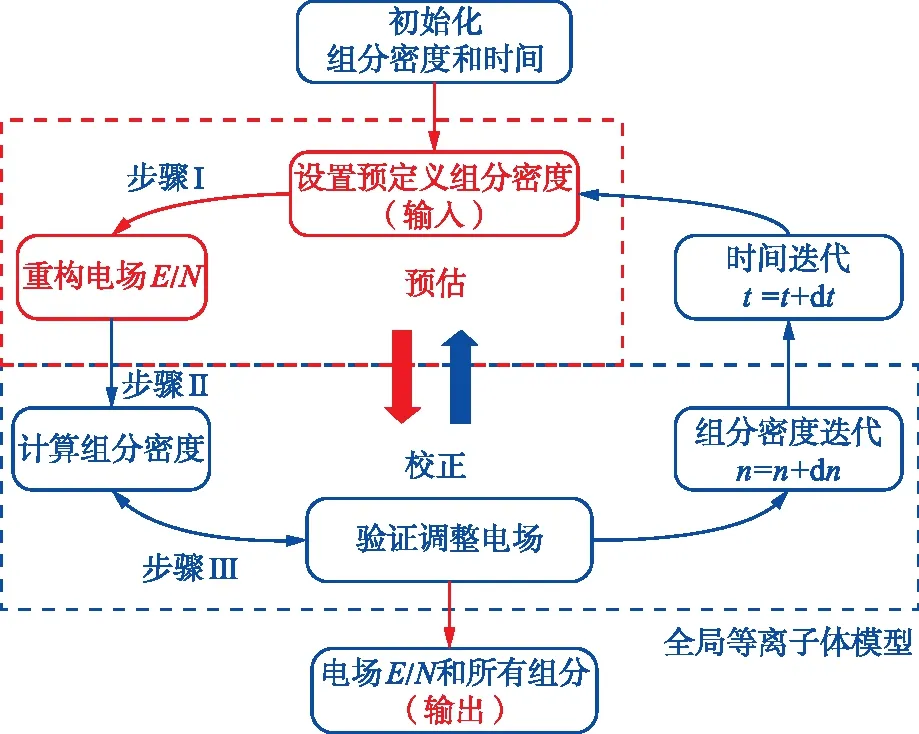
图1 DeePlaskin框架
1)全局等离子体模型产生大量组分密度随时间演化数据供深度神经网络进行训练,当深度神经网络训练完成后,初始化所有组分密度并设置预定义的组分密度,根据预定义的组分密度,利用深度神经网络模型来逆向求解出电场。
2)把深度学习预测的电场输入全局等离子体模型中计算各组分密度,验证组分密度是否在设定的允许误差范围内,若满足误差要求则输出预估电场和组分密度。
3)若电场不满足误差要求则进行迭代校正,把校正过后的电场输入全局等离子体模型中重新计算组分密度至满足所允许的误差要求,最后输出电场和各组分密度。
2 模型的建立与验证
2.1 二维模型
本文中的火花放电模型参考了文献[28],文献中实验气压为100 Torr(1 Torr=133.322 4 Pa),温度为300 K,电压是峰值为10 kV频率为10 kHz的纳秒脉冲电压,对空气(N2∶O2)进行放电。放电结构由2个直径7.5 mm的球金属电极组成,两电极间距为10 mm,具体结构如图2(a)所示。把实验所测电压作为二维模型的输入电压,初始背景电子密度为ne0=105m-3。需要考虑的边界条件是求解输运方程的边界条件和求解Poisson方程的边界条件,输运方程的边界条件如表1所示,Poisson方程的边界条件有2个:Dirichlet 和 Neumann 边界条件,前者是金属边界V=V(t),后者是∇V= 0,其中 Dirichlet 边界条件涉及到对金属几何形状的精确表述,而 Cartesian 网格在曲面电极形成的是锯齿状网格。仿真计算结果和实验测量发光半径如图2(b)所示结果基本吻合,其次对比了计算电流和实验所测电流,如图2(c)所示总体吻合良好。
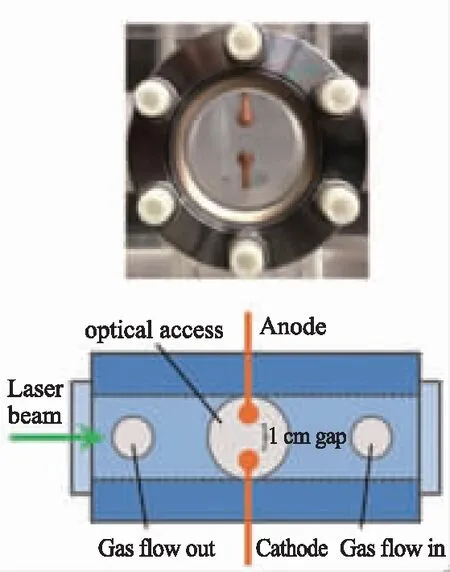
(a)实验放电腔和几何示意[28]

表1 输运方程的边界条件
电子密度的时空演化结果如图3所示,106 ns附近放电通道形成,流柱贯通两电极,此时电场分布基本均匀,但是在通道形成后一段时间,电子密度和电场快速减小,放电通道收缩,火花有熄灭的趋势。

图3 电子密度随时空的演化
2.2 零维模型
由于二维计算代价较大且忽略了一些重要反应信息,为了进一步观察电子和其他粒子随时间的演化以及火花的发展趋势,使用零维模型进行计算。如图4所示,在图4(a)二维模型通道导通时刻选取计算域中间点,电场随时间的演化结果如图4(b)红线所示,选取图4(b)中的3个时刻t1、t2、t3对应的电子密度分别为1×1013cm-3、5×1012cm-3、1×1012cm-3,以这3个时间所对应的频率作为放电频率,使电子密度在数十纳秒内增长至1×1015cm-3,用以维持火花放电。

(a)PASSKEy计算电场二维
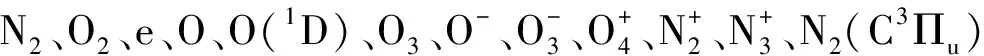
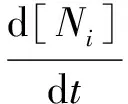
(6)
零维反应动力学求解结果如图4(b)所示,图中列出了第一次火花放电后残余粒子对第二次放电起决定性作用的粒子:
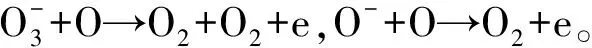
2.3 反应动力学模型耦合深度学习模型
供给深度学习模型训练的海量数据来源于ZDPlaskin求解常微分方程组,产生数据时工况一定(T=300 K,p=100 Torr),主要是以覆盖尽可能多的电场波形为主,如式(7)所示:
(7)
式中:E/N(t0)=0.5;Ap=5.0+2.5M;tc=10K;
式(7)共产生1 000个文件,每个文件包含10 000个时间步长的约化电场E/N和粒子数密度,数据分为2个部分:80%用来学习,20%用来验证,测试数据是以上实验数据。
反应动力学对应的常微分方程组见式(8):
n(t+dt)=f(E/N(t),n(t),dt)
(8)
式中:n(t)为t时刻的各组分密度;E/N(t)为t时刻的电场;dt为时间步长;n(t+dt)为t的下一时刻的各组分密度,在给定电场和初始值后会根据时间步长求解下一时刻的组分密度。
式(8)是强刚性的常微分方程,不同组分密度之间相差10几个数量级,组分之间存在耦合关系,且是高度非线性的。深度学习模型逆向求解电场如式(9)所示,通过t+dt时刻的组分密度对数来逆向求解t时刻的电场E/N。
E/N(t)=f(log(n(t+dt)),dt)
(9)
深度学习模型如图5(a)所示,1个4层的深度神经网络(DNN),输入向量为65维,全连接层分别为400、256、256层,输出向量为63维,激活函数为ReLU,损失函数为平均绝对误差(MAE),选用了学习率为0.001的Adam优化器,为防止过拟合加了L2正则化,总共训练200个周期,训练和验证误差如图5(b)所示,可以看到误差在10-4数量级。

(a)深度神经网络模型
利用训练完成的神经网络来重构电场,结果如图6(a)所示。电子密度自定义从1012cm-3增长到1015cm-3(蓝线),重构出的约化电场经过平滑处理后如图中红色曲线所示。通过电场计算出的电子密度(蓝色圈)与原波形完全吻合,再根据此计算出的电场算出电压(绿线),把电压作为二维模型的输入计算整个放电过程,如图6(b)所示在50 ns放电过程中电子密度与基准基本重合。
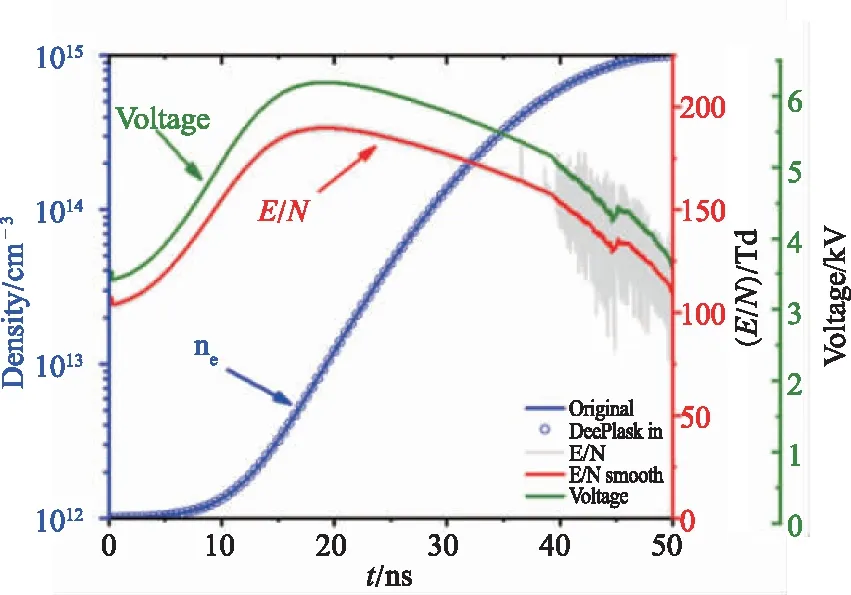
(a)DeePlaskin重构电场
3 结果与讨论
等离子体反应动力学模型可以实现对放电效果的预测,确定影响点火助燃过程最显著的活性物质,而从应用的角度出发,则应当以所需活性物质为优化目标实现等离子体点火助燃反应器的优化调控,为了实现该目标,建立神经网络模型,实现针对电子密度随时间演化的电压波形重构,从而优化等离子体反应器的电源电压,使其点火助燃过程中既放电能耗低又能产生足够多的目标组分。
3.1 针对频率调节火花放电
在等离子体点火助燃中维持火花放电产生可靠连续的热效应和化学效应,即电子密度需要在每个周期内维持在一定范围(1012~1018cm-3)。图7为球球放电在第1个放电周期内电子密度随时间演化曲线,电子密度从1015cm-3持续下降,在其中分别选取t1=1 146 ns、t2=1 718 ns、t3=3 934 ns作为放电第2个周期的初始时刻,即所对应的放电频率为f1=872.6 kHz,f2=582.1 kHz和f3=254.2 kHz。使其3个放电频率内电子密度都以高斯函数增长至1015cm-3以维持第2个周期内的火花放电,通过Deeplaskin模型基于电子密度反向求解电场,从而进一步推算出所对应的电压,结果如图7(b)、(c)、(d)所示。从图中可以分别看到3个频率下放电所对应的电压波形基本相似,电压峰值有所不同,其分别为5.81 kV、5.47 kV和5.2 kV,相较于频率f1,频率f2和f3的初始电子密度分别增加了5倍和10倍,所对应的电压幅值分别减少了5.96%和9.18%,电压幅值的增长率与电子密度的增长率成负线性关系。另外可以发现当初始电子密度增大时,气体放电所需的击穿电压越小,但当电压降低时,两电极间气体击穿时间将会增大,这是因为在第2个周期放电时上一次放电产生的残余电子会加强电子崩的传播,使其快速流向电极形成放电通道。在等离子体反应器中针对不同频率放电,我们需要调节电源电压幅值以及考虑所需击穿时间。
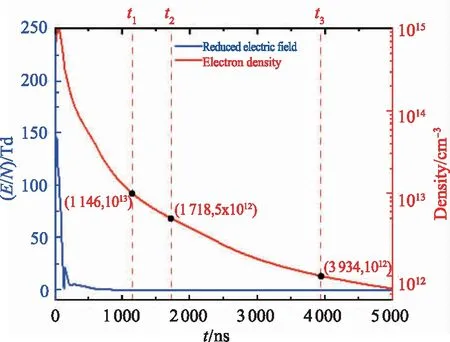
(a)E/N and Density
3.2 针对电子密度增长方式调节火花放电
以电子密度为优化目标,逆向调节火花放电助燃反应器的电源电压波形。为了调节火花放电使其持续稳定,使电子密度在第2个周期50 ns内从初始密度1012增长至1015cm-3,我们设计了4种不同的电子密度增长方式,如图8(a)所示。这4种电子密度曲线代表了4类增长方式:线性增长、先慢后快、先快后慢、分段增长。
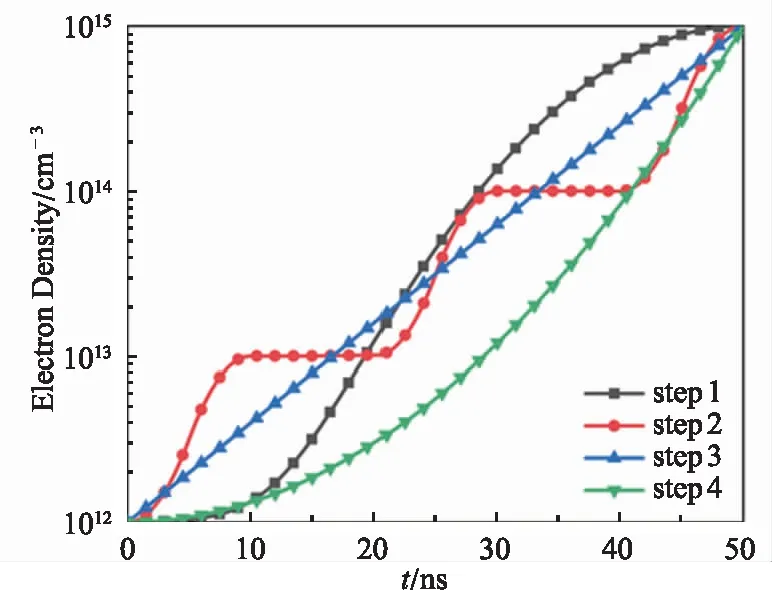
(a)Mode of ne growth
第1种增长方式为高斯函数,见式(10):
(10)
式中:a为高斯曲线的峰值(a=1015);b为尖峰中心坐标(b=50);c为标准方差,表征的是bell钟状的宽度(c=0.1)。
第2种是相较于y的对数以阶梯式增长所示。
第3种是相较于y的对数以直线增长,见式(11):
log(y)=0.06x+12
(11)
第4种是相较于y的对数以二次函数形式增长,见式(12):
(12)
以上4种电子密度曲线都是在0~50 ns内电子密度从1012增长至1015cm-3。
在图8(b)中是4种增长方式所对应的能量消耗,使用深度学习重构出电场将其代入零维模型计算出功率密度,功率密度在时间积分下的单个分子所消耗的能量,对应的能耗值分别为0.295、0.157、0.205和0.152 eV/mol,可以看到第2、4种增长形式对比其他两种能量消耗明显较小,比第1种增长方式能耗几乎小了1倍。初步分析是因为电子崩传播阶段电子密度是以指数形式增长,前期电子密度本身就低,若想提高前期电子密度需要额外能量输入,因此前快后慢的电子密度增长方式需要消耗更多的能量。在等离子体点火助燃中,不能只考虑能耗的影响,也应该考虑等离子体化学效应促进助燃,等离子体放电产生的高能电子、离子和激发态的粒子可以有效地将大分子碳氢燃料裂解重整为小分子,既改变了燃料分子的化学活性,又改变了燃料的输运特性,从而在很大程度上改变了燃烧的特性。比如O原子和O(1D)都可以改变燃烧化学的反应路径加快燃烧。在不同的电压波形下,这些重要粒子密度随时间演化是有所区别的,如图8(c)、(d)所示,从图中可以明显看出第1、2种电压波形所产生的O原子和O(1D)粒子数较多,更有利于助燃。因此综合考虑能耗和所产生的粒子数密度的影响,第2种分段式增长的电子密度所对应的电压波形更适合火花放电点火助燃。
4 结语
1)本文所建立的等离子体反应动力学模型和二维流体模型,较完整地描述了1 μs内球球放电等离体子的物理化学过程,计算结果与实验所测电流和光谱数据进行了对比验证,此模型较好地展示了气体放电中各粒子随时空演化的过程。
2)等离子体反应动力学模型可以实现对放电效果的预测,确定影响点火助燃过程最显著的活性物质,而从应用的角度出发,则应当以所需活性物质为优化目标实现等离子体点火助燃反应器的优化调控,为了实现该目标,建立神经网络模型,实现针对电子密度随时间演化的电压波形重构,从而优化等离子体反应器的电源电压。
3)本文计算分析了放电频率和电子密度增长方式对火花放电的影响。通过神经网络模型计算得到电压幅值的增长率与初始电子密度的增长率成负线性关系;电子密度增长方式中先慢后快和分段增长比线性增长和先快后慢更节省放电能量;而电子密度分段增长所对应的电压下放电所产生的O原子和O(1D)粒子数较多,更有利于助燃。根据计算结果,从能耗和所产生的活性粒子密度来看,分段增长的电子密度所对应的放电电压波形更适合火花放电点火助燃。

