基于随机有限集的视频SAR多目标跟踪方法
陈李田, 张 云, 李宏博, 王 勇
(哈尔滨工业大学电子与信息工程学院,哈尔滨,150006)
随着合成孔经雷达(synthetic aperture radar,SAR)技术的不断发展,SAR图像目标自动识别、目标自动跟踪相关研究逐渐成为焦点[1]。近年来,高分辨合成孔径雷达相关技术得到快速发展[2],并衍生出了高分辨视频SAR技术。视频SAR在对地侦测领域具有不可比拟的优势,它能够以近似光学的方式获取地面感兴趣区域的持续观测,更容易获取位于监测场景中的各种目标的相关信息[3],对基于SAR图像的目标识别与跟踪的研究起到了积极的推动作用。为了满足更高的应用需求,多目标跟踪技术逐渐发展成熟。在多目标跟踪过程中,每个目标的运动状态都有可能变化,且目标数量具有随机性,因此多目标跟踪需要在对监测区域内的目标状态进行预测和更新的同时也获取目标数量的变化情况,这对跟踪算法的性能提出更高的要求。
针对上述需求,基于随机有限集(random finite set,RFS)的视频SAR多目标跟踪技术成为跟踪领域的研究热点。其基本原理是在视频SAR系统中,利用有限集统计学将RFS的概念引入视频SAR多目标跟踪算法中,用有限集表示目标的状态集与量测集,并通过贝叶斯框架估计下的高斯混合概率假设密度(Gaussian mixture-probability hypothesis density,GM-PHD)等次优滤波[4]方式实现状态估计和更新,并对目标数量做出了预测。该方法将目标的状态集合用RFS表示,本身就可以对状态不确定和数量不确定的目标集合进行表示,不涉及传统算法的关联步骤,在复杂背景环境下具备较好的跟踪性能。
多目标RFS跟踪算法最早是由Ronald Mahler[5]所提出的,典型代表分别为矩近似的PHD滤波[6]和CPHD滤波[7]算法以及密度近似的多伯努利滤波[8]算法。基于随机有限集的多目标跟踪算法近年来得到了充分了发展。文献[9]设计了一种基于随机有限集的新的概率假设密度(probability hypothesis density,PHD)滤波器,通过对目标航迹的调整重组,有效提高了提取多目标航迹的准确度,进而提高了雷达在复杂背景下的持续跟踪性能。文献[10]提出了一种适用于SAR系统的基于RFS的改进高斯混合PHD滤波器的动目标跟踪方法,可以实现准确估计运动目标数量和状态,并实现运动目标轨迹的提取。本文在随机有限集条件的背景下,通过对GM-PHD等次优滤波方式的研究,提出了一种适用于视频SAR连续多帧序列的基于随机有限集的多目标跟踪方法。
1 多目标贝叶斯框架估计理论
1.1 基于RFS的视频SAR多目标跟踪系统
多目标跟踪不仅需要估计当前时刻各目标的运动状态,还需要关注目标数量。由RFS基本概念可知,有限集中包含的元素数量是随机值,与多目标跟踪中目标数量未知的特点十分契合,所以在RFS的基础上构建多目标跟踪系统。基于RFS的视频SAR多目标跟踪系统模型如图1所示。

图1 视频SAR多目标贝叶斯跟踪系统模型
1.2 多目标运动模型和观测模型
在目标跟踪的过程,每一时刻目标都有可能发生变化,存在4种变化的可能性,分别是目标运动,目标消失,目标新生以及目标衍生。对目标被观测到的情况也分为3种:观测到目标信息(似然)、未观测到目标信息(漏检)和观测到错误信息(杂波)。目标运动模型和观测模型示意图如图2所示。
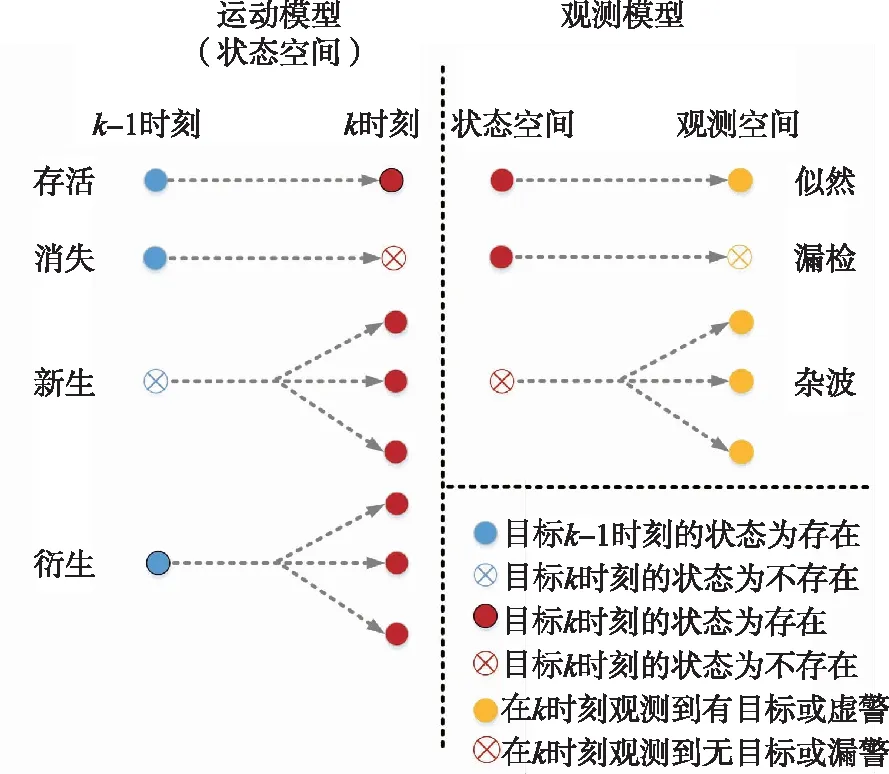
图2 目标运动模型和观测模型示意图
在本文构建的基于RFS的多目标跟踪系统中,主要考虑对线性运动目标的监测跟踪,且该类目标自身状态大概率会出现存活、消失和新生3种情况,但不排除因为目标交会分离等原因出现目标衍生的情况。此外,在观测过程中,由于相干斑噪声等影响,会出现漏警或者虚警的情况,即目标观测过程中存在似然、漏警和杂波3种情况。上述的目标类型、目标状态集合以及目标观测集合共同组成了本文所搭建的系统模型。
1.3 多目标贝叶斯滤波原理
多目标贝叶斯滤波是基于RFS的多目标跟踪理论的重要部分之一,基本思路是需要在递推出当前时刻多目标的后验概率密度的基础上,通过对后验概率密度进行积分估计出当前时刻监测区域内目标的运动状态和数量。整个过程的预测和更新递推方程分别为:
fk|k-1(Xk|Z1:k-1)=
(1)
fk|k(Xk|Z1:k)=
(2)
式中:fk|k-1(Xk|Xk-1)表示状态转移概率密度函数;gk|k-1(Zk|Xk)表示目标似然函数;Z1:k={Z1,Z2,…,Zk}表示直到k时刻的观测积累。
从预测和更新递推方程式中可以发现,基于RFS的多目标贝叶斯滤波涉及到对不确定维数集合的积分,随着目标状态RFS包含元素数量的增长,递推计算量会呈现出数值爆炸的趋势。因此,该方法很难在工程中实现,需要通过对基于多目标RFS的贝叶斯滤波算法进行近似,在确保跟踪性能的前提下使算法变得较为容易实现。
2 基于RFS的GM-PHD滤波算法
2.1 基于随机有限集的PHD滤波算法
PHD是后验概率分布的一阶统计矩,也称之为强度函数。假设fk(Xk|Z1:k)是多目标状态有限集的后验概率密度函数,则其PHD可以表示为:
(3)
式中:δx(x)为狄拉克函数。
在监测区域S内对v(x|Z1:k)进行积分就可以得到区域内期望的目标数量的估计值N(S),即目标数量估计方程式为:
(4)
为了简化多目标状态空间结构中所有不确定维数的多维复杂积分,可以通过引入RFS,利用多目标强度函数v(x|Z1:k)替换滤波递推过程中的概率密度,将多维复杂积分简化为单目标状态空间结构上的单一积分,有效提高滤波效率。具体流程如下:
首先在Poisson分布的假设条件下由式(1)和式(2)可以得到PHD滤波算法的预测方程和更新方程分别为:
vk|k-1(xk|Z1:k-1)=
(5)
vk(xk|Z1:k)=
(1-pD,k(xk))vk|k-1(xk|Z1:k-1)+
(6)
式中:pS,k(xk)为目标运动的概率;pD,k(xk)为目标检测概率;βk|k-1(xk|xk-1)和γ(xk)分别为从衍生和新生目标随机集的PHD;Kk为杂波随机集的PHD。
在得到当前时刻多目标RFS的强度函数vk(xk|Z1:k)之后,由式(4)可以估计出当前时刻监测区域内目标的数量:
(7)
基于随机有限集的PHD滤波有很多优点,比如:可以不通过数据关联便对多个目标的运动状态进行估计;可以对数量未知的多目标集合进行跟踪,自适应监测区域内目标数量的变化等。文献[11]指出PHD滤波是建立在Poisson分布假设上的,这就导致了在递推迭代方程式中仍然存在多维的向量积分,要得到PHD滤波闭合解的解析形式还是比较困难的,并且容易引起维数灾难,但可以通过GM-PHD滤波解决上述问题。
2.2 基于随机有限集的GM-PHD滤波
为了优化PHD的滤波效果,本文采用通过建立高斯混合(gaussian mixture,GM)模型的方法,在PHD滤波递推过程中用GM参数替代PHD进行递推迭代,可以得到闭合解,进而优化滤波效果。
对于线性的多目标跟踪系统,每一个目标的运动模型的状态转移函数和传感器的观测模型的似然函数均满足GM模型:
fk|k-1(x|η)=N(x;Fk-1η,Qk-1)
(8)
gk(z|x)=N(z;Hkx,Rk)
(9)
式中:N(·)表示GM分布;η是前一时刻目标的状态;Fk-1是状态转移矩阵;Hk是观测矩阵;Qk-1和Rk分别为内部噪声和外部噪声的协方差矩阵。
新生目标和衍生目标的PHD也需要满足GM模型:
(10)
(11)
式中:Jγ,k,wγ,k,mγ,k,Tγ,k为GM模型下新生目标的属性,共同描述了新生目标的PHD。同样的,Jβ,k,wβ,k,Fβ,dβ,k和Tβ,k描述了衍生目标的PHD。
此时,在GM模型下k时刻多目标的预测强度函数为:
vk|k-1(x)=vS,k|k-1(x)+vβ,k|k-1(x)+γk(x)
(12)
式中:vS,k|k-1(x),vβ,k|k-1(x),γk(x)分别是目标运动、衍生和新生的预测PHD。
对于vS,k|k-1(x),其预测公式为:
(13)
(14)
(15)
同样,vβ,k|k-1(x)和γk(x)的预测公式为:
vβ,k|k-1(x)=
(16)
(17)
经过对vS,k|k-1(x),vβ,k|k-1(x)和γk(x)的计算之后,可以得到高斯混合模型下k时刻多目标的预测PHD为:
(18)
然后利用k时刻传感器获得的GM模型下的量测对多目标的vk|k-1(x)进行更新。k时刻多目标RFS后验概率密度的强度函数为:
(19)
vD,k(x;z)是传感器量测RFS的强度函数,其GM形式的表达式为:
(20)
(21)
(22)
(23)
综上,可得k时刻多目标RFS后验概率的PHD:
(24)
式中:Jk=Jk-1+Jβ,k+Jγ,k
3 实验结果与分析
为验证本文提出的基于随机有限集的视频SAR多目标滤波跟踪方法的有效性,通过实测1组视频SAR图像序列,进行跟踪验证,其中关键参数如表1所示。
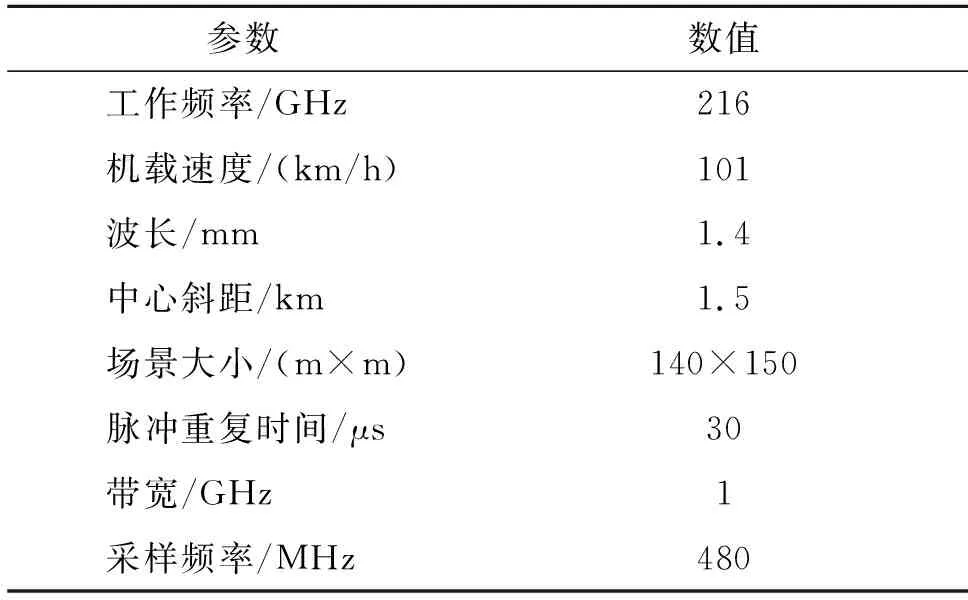
表1 视频SAR系统参数
实验共选取连续的30帧SAR图像序列,其中图3是该图像序列中间的某一帧(配准后),作为场景示意图说明场景中的目标运动信息。

图3 场景及目标运动状态示意图
如图3所示,这是本文实验所用视频SAR连续多帧图像序列中的某一帧,可以看出这是一个十字路口,在图示时刻的附近几帧中共有4个目标,分别标记为目标1、目标2、目标3和目标4,在该配准坐标系下目标1、3、4沿y轴负半轴方向运动,目标2沿着x轴正半轴方向运动。其中,目标1从第1帧已经存在到第23帧左右消失;目标2在这30帧中一直存在;目标3从第5帧左右出现后一直存在;目标4从第15帧左右出现后一直存在。基于此,结合目标检测所得目标位置信息,可以先估计出目标的运动轨迹,如图4所示。需要注意的是,本次实验是定性分析,使用的是像素点位表示的目标位置,约为0.13 m/像素。
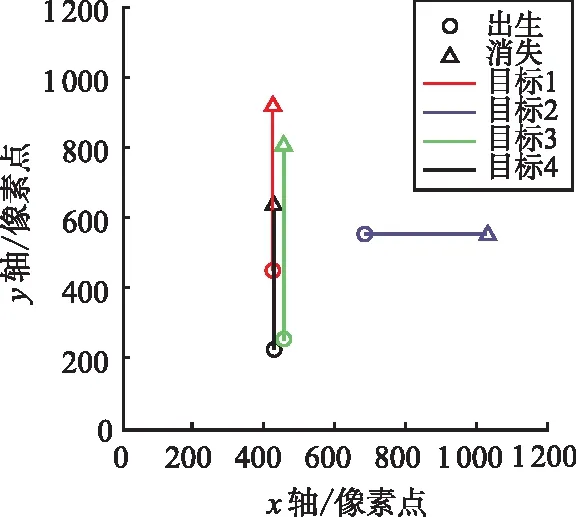
图4 目标运动轨迹
然后进行基于随机有限集的GM-PHD滤波实现这4个目标的跟踪,需要得到检测区域的量测信息以及目标的新生强度信息,其中量测是基于阴影检测算法提取的阴影信息;目标的新生强度则是通过目标阴影的位置信息以及大小所占量测总像素点数量的比值近似估计目标的强度信息。为了方便观测到每个目标的跟踪情况,本实验对各目标进行了标签处理,实验结果见图5。
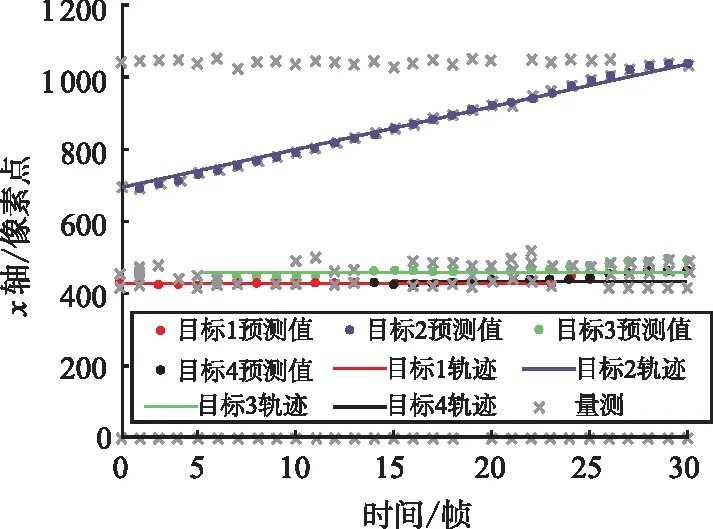
(a)目标x轴跟踪结果
在图5中,不同颜色的直线代表的是图4中所估计的不同目标的运动轨迹,相应颜色实心点表示跟踪到的相应目标,灰色叉点表示杂波或虚警。
然后进行误差分析。第5帧、第15帧还有第25帧存在误差的原因是因为上述讨论目标数量的起始和消失帧数有所偏差,与跟踪算法的性能无关;第12帧时丢失了对目标3的跟踪,第21帧丢失了对目标4的跟踪,但由于算法在不断的预测与更新,在下一帧又重新对目标实现了跟踪;第19帧、第21帧和第23帧出现了错误的新生或衍生判断,由于目标当时位置与杂波位置较近,出现了误判现象,随着算法的更新修正,自动矫正了该错误,说明该跟踪方法具有一定的自纠正能力;第21帧~第24帧,由于目标1到了图像边缘,杂波影响较大,所以出现了明显的误差,该跟踪方法在边缘处理上有待改进。图6给出了每个目标的跟踪情况。
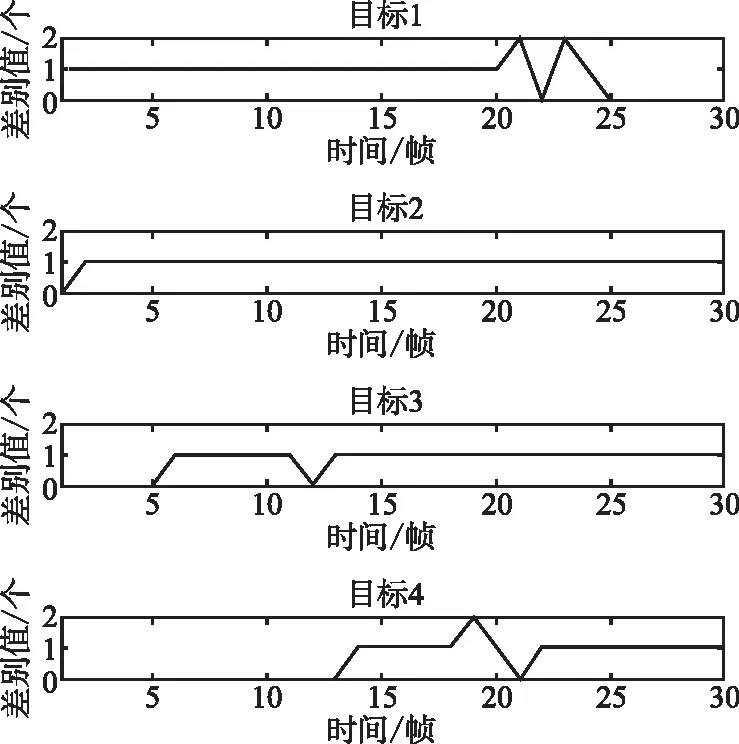
图6 每个目标的跟踪情况
如图6所示,判别值为1说明该帧正常跟踪到了该目标,判别值为0说明该帧没有该目标或者该目标消失了,判别值为2说明跟踪时判定该目标发生了衍生或出现了其他新生目标。根据图6所示情况,可以进一步得到本次实验对多目标目标跟踪估计的准确率约为93.63%。
为了更好地展示该跟踪算法的性能,本实验通过最优子模式分配距离(optimal subpattern assignment,OSPA)对目标的GM-PHD滤波估计结果集合的脱靶距离进行测量,结果如图7所示。
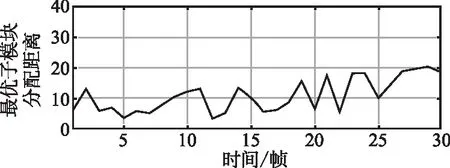
图7 跟踪结果的OSPA距离
从图7可以看出,该算法的OPSA距离均小于25像素点,即小于3 m,一定程度上说明了本算法的可行性与有效性。
最后在成像场景下展示该跟踪算法的效果,仍用红色表示目标1,蓝色表示目标2,绿色表示目标3,由于图像背景较暗,目标4改用白色表示,结果如图8所示。

图8 跟踪结果展示
4 结语
本文探索了基于随机有限集的多目标跟踪算法在视频SAR系统中的应用。在基于RFS的多目标跟踪系统结构和目标模型下,分析了多目标贝叶斯的原理;然后为了实现基于RFS的多目标跟踪算法,讨论了贝叶斯框架下的PHD算法,并在GM模型下得到了适用性较强的GM-PHD算法。最后在上述讨论的基础上,结合一组视频SAR连续多帧图像序列,实现了对该组图像序列中4个目标的跟踪,验证了基于RFS的多目标跟踪算法在视频SAR连续多帧图像序列中实现多目标跟踪的可行性。

