基于改进蚁狮优化的贝叶斯网络结构学习算法
陈海洋, 尚珊珊, 任智芳, 刘 静, 张 静
(西安工程大学电子信息学院,西安,710048)
贝叶斯网络(bayesian network,BN)是基于概率推理的图形化网络,通过数据统计、建模分析、计算推理来解决不确定性和不完整性问题[1-2],主要应用于故障溯源、医学诊断、军事智能等领域[3-7]。BN的基本理论研究分为3个方面:结构学习、参数学习和推理,其中,结构学习作为BN的基础与核心,目的是从数据中获得最能体现变量间关系的有向无环图。目前,结构学习的方法主要分3种:①基于约束的方法[8-9],通过适配测试函数来判断变量间的依赖关系,并作为约束进行结构学习;②基于评分函数的方法[10-11],将学习到的模型与已知信息的拟合程度进行量化,根据评分函数打分,分值最高的为最优结构;③混合的方法[12-13],首先根据方法①初始化网络,然后选择适合的搜索策略,通过方法②继续更新寻找最优解。由于特定需求或者特殊环境等因素的限制,如涉及军事防御等重要场合的战场态势评估、可获得数据较少的电力系统设备故障分析以及罕见疾病诊断等领域,数据的获取相对困难,因此,需要在小数据集条件下对BN结构学习展开研究。小数据集下的BN结构学习主要是通过引入专家经验或领域知识形成约束,进而结合优化算法将先验约束融入到结构学习中[14-15],以此来提高BN结构学习的准确度。
Seyedali Mirjalili学者于2015年提出了蚁狮优化算法(ant lion optimizer,ALO)[16],因其求解精度高、参数调节容易的特点,被广泛应用于众多工程领域[17-18]。文献[19]采用具有自适应的柯西变异算子使得蚁狮个体受局部极值点约束力下降,快速跳出局部最优,提高了搜索效率;文献[20]针对蚁狮算法探索与开发能力不平衡的缺点,提出了具有自适应边界与最优引导的莱维飞行改进算法,提高了收敛速度和全局搜索能力。上述改进方法虽然使蚁狮优化算法的性能得到优化,但是无法结合各种形式的先验知识,不适用于数据量较小的BN结构学习。
针对蚁狮算法易陷入局部最优的缺点,同时为了有效利用小数据集,本文对蚁狮算法进行改进并应用于BN结构学习过程,提出基于改进蚁狮优化的贝叶斯网络结构学习算法(improved sigmoid function and fusion of the BBO mechanism and the ant lion algorithm,ISB-ALO)。
1 相关概念
1.1 互信息
互信息(mutual information,MI)可以衡量节点间的关联程度。互信息值越大,关联性越强,互信息值为零时,节点相互独立。变量X和Y之间的互信息用I(X,Y)表示,且对任意两个离散随机变量X和Y,有I(X,Y)>0,表达式如式(1)所示:
I(X,Y)=H(X)+H(Y)-H(X,Y)
(1)
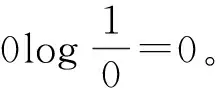
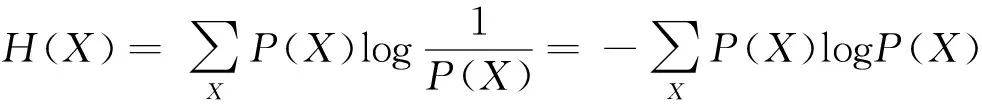
(2)
(3)
(4)
1.2 BN结构表达以及sigmoid函数
贝叶斯网是一个有向无环图,其中,将节点视为随机变量,节点的连接边表示变量之间的因果关系,高晓光等在文献[21]中提出有向无环图及其位置表示的方法如图1所示。
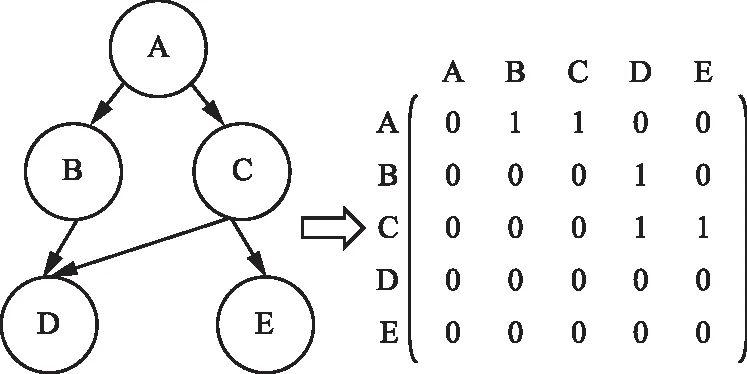
图1 有向无环图及其位置表示
图1对应的矩阵G(n,n)中,元素gij的取值与各节点连接关系用式(5)表示:
(5)
式中:gij是G(n,n)中第i行第j列的元素。
由式(5)可知,矩阵元素只能用0和1表示,但算法迭代时数值复杂多变,因此有学者用sigmoid函数对其进行转换,式(6)为sigmoid函数表达式:
(6)
式中:Vij∈[-Vmax,+Vmax],通常Vmax取4。
1.3 基本蚁狮算法
ALO模拟蚁狮对蚂蚁的狩猎机制来实现寻优,精英蚁狮的位置相当于优化问题的解,蚁狮通过捕猎高适应度的蚂蚁实现对近似最优解的更新和保存,该过程被模拟为以下5个部分:
1)蚂蚁随机游走机制
根据式(7)的随机游走机制定义蚂蚁的位置:
(7)
式中:Csum是计算累积和的函数;n是迭代最大次数;t是随机游走的步长;r(t)是一个[0,1]之间的随机函数。
2)蚁狮构建陷阱
蚂蚁的随机游走受蚁狮陷阱的影响为:
(8)
(9)
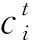
3)蚁狮捕捉蚂蚁
一只蚂蚁只会被困在一只选定的蚁狮陷阱中,优化过程中利用轮盘赌策略根据适应度来选择蚂蚁。蚁狮建立与其适应度成比例的陷阱,对适应度高于自己的蚂蚁进行捕猎。
4)蚁狮重驻陷阱
狩猎完成后,为增加捕猎的机会,蚁狮会将位置更新到适应度高于自己的蚂蚁的位置:
(10)
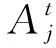
5)精英机制
每次迭代中的最佳蚁狮被保存下来作为精英蚁狮。每个蚂蚁的游走都会受到由轮盘赌选出的蚁狮与精英蚁狮的影响:
(11)
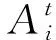
2 ISB-ALO算法构建
2.1 互信息约束算法的初始结构
为了缩小蚁狮算法搜索范围,提高搜索效率,引入互信息约束。首先,根据式(1)~式(4)计算出各节点之间的互信息,根据互信息值的大小判断出最优BN结构的候选边。其次,将选定的边作为约束,加入随机生成的网络中,初始化蚂蚁和蚁狮的位置,生成基于蚁狮算法的结构搜索空间。
2.2 小数据集下sigmoid函数的改进
ALO中蚂蚁与蚁狮的位置更新可看作BN结构变化的过程。在对矩阵元素进行二值转换时,由于受sigmoid函数速度边界Vmax的限制,部分超出取值范围的数据可能丢失,因此,为提高结构学习的效率、充分利用小数据集,提出对数据划分更详细的转换方法:先根据式(12)将矩阵G(n,n)中的元素gij投影在sigmoid函数的自变量范围内,再利用sigmoid函数将G(n,n)转换为元素在[0,1]之间的矩阵G′(n,n),进而根据式(13)通过蚁狮精英机制寻优。
(12)
(13)
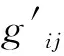
2.3 融合BBO机制的蚁狮算法
生物地理算法(biogeography-based optimization,BBO)[22]中,动物根据适应度的高低选择迁入与迁出。将BBO中迁入率与迁出率视为与个体适应度相关的线性函数,对算法中迁入、迁出、消亡等过程,分别建立迁移算子、变异算子、清除算子,并融合到蚁狮算法迭代过程中,来平衡局部最优与全局最优的关系。
2.3.1 迁移算子
在BBO的基础上引入迁移算子,用根据迁出率选择的蚂蚁替换轮盘赌选出的蚂蚁。蚂蚁i的适应度比重与迁入率、迁出率的函数关系分别见式(14)和式(15),模型见图2,迁移算子流程见表1。

表1 迁移算子流程
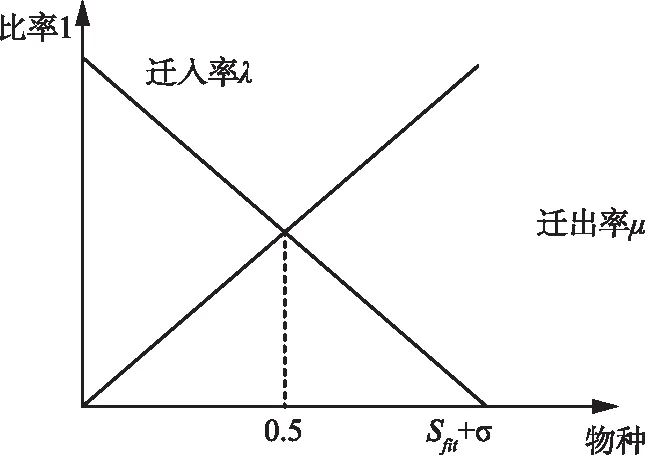
图2 物种迁移模型
(14)
λ=1-μ
(15)
式中:ft为蚂蚁i的适应度;Sfit为总适应度;λ为迁入率;μ为迁出率;σ为极小值常数。
2.3.2 变异算子
在BBO中,蚂蚁的适应度在总适应度中占比越高,陷入局部最优的可能性越大,因此,用互信息约束的蚂蚁取代根据变异概率选择的蚂蚁,来减小陷入局部最优的概率,定义变异概率公式见式(16),变异算子流程表2。

表2 变异算子流程
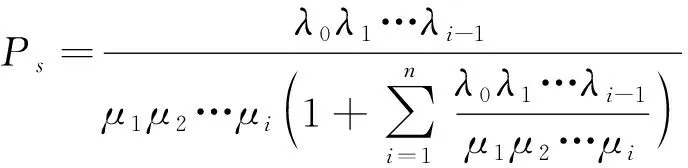
(16)
式中:Ps为变异概率;λj(j=0,1,…,i-1)为迁入率;μj(j=1,2,…,i)为迁出率。
2.3.3 清除算子
清除算子根据适应度的大小选择被替代的蚂蚁,若蚂蚁j的适应度值等于蚂蚁i,则用加入互信息约束的蚂蚁替代i,清除算子流程见表3。

表3 清除算子流程
2.4 ISB-ALO算法
ISB-ALO算法流程见图3。
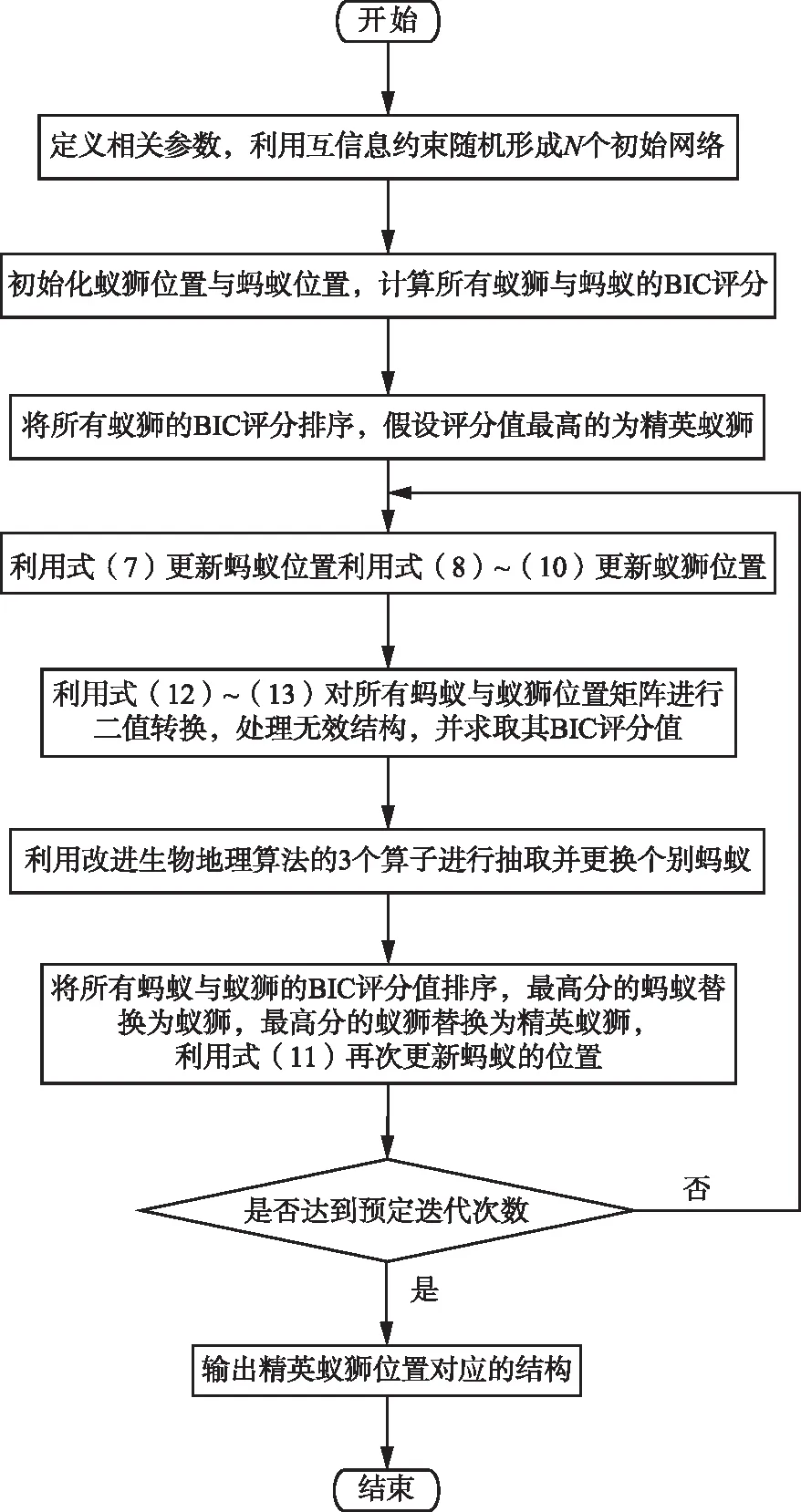
图3 算法流程图
3 仿真结果及分析
3.1 算法验证
为了验证本文ISB-ALO算法的寻优性能,用4个具有单峰、多模态、高维和低维等特点且理论极值均为0的测试函数验证,将该算法的寻优曲线与混沌粒子群算法、鸟群算法、混合蚁狮算法进行对比,各算法参数设置见表4,迭代次数均为2 000次,实验结果见图4。
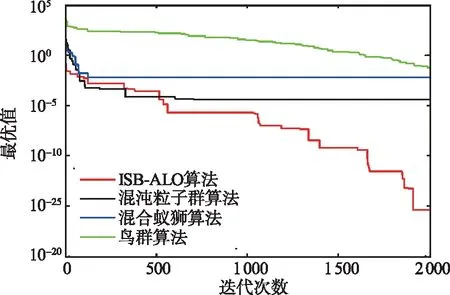
(a)Ackley函数

表4 实验参数设置
测试函数如下:
1)Ackley函数
(17)
2)booth函数
xi∈[-5.12,5.12]
(18)
3)Sphere函数
(19)
4)Zakharov函数
xi∈[-5,10]
(20)
根据图4可知:混沌粒子群算法以及混合蚁狮算法在迭代未结束时就停止更新,而鸟群算法以及ISB-ALO算法可以不断迭代直至最优值。由于引入了BBO机制,ISB-ALO算法搜索能力较鸟群算法更强,不同测试函数下该算法的寻优结果均优于对比算法,且不会陷入局部最优解。
为了避免实验的随机性,每组实验分别运行50次,将各算法寻优结果的最好值、最差值、均值、标准差的平均值进行对比,见表5所示。
根据表5可知,相较于鸟群算法、混沌粒子群算法以及混合蚁狮算法,ISB-ALO算法最优值、最差值、均值、标准差的平均值均低于对比算法,并且最优值更接近测试函数的理论极值。综上所述,ISB-ALO算法不论是寻优曲线还是最终结果均优于其它算法,证明了融合BBO机制的有效性。
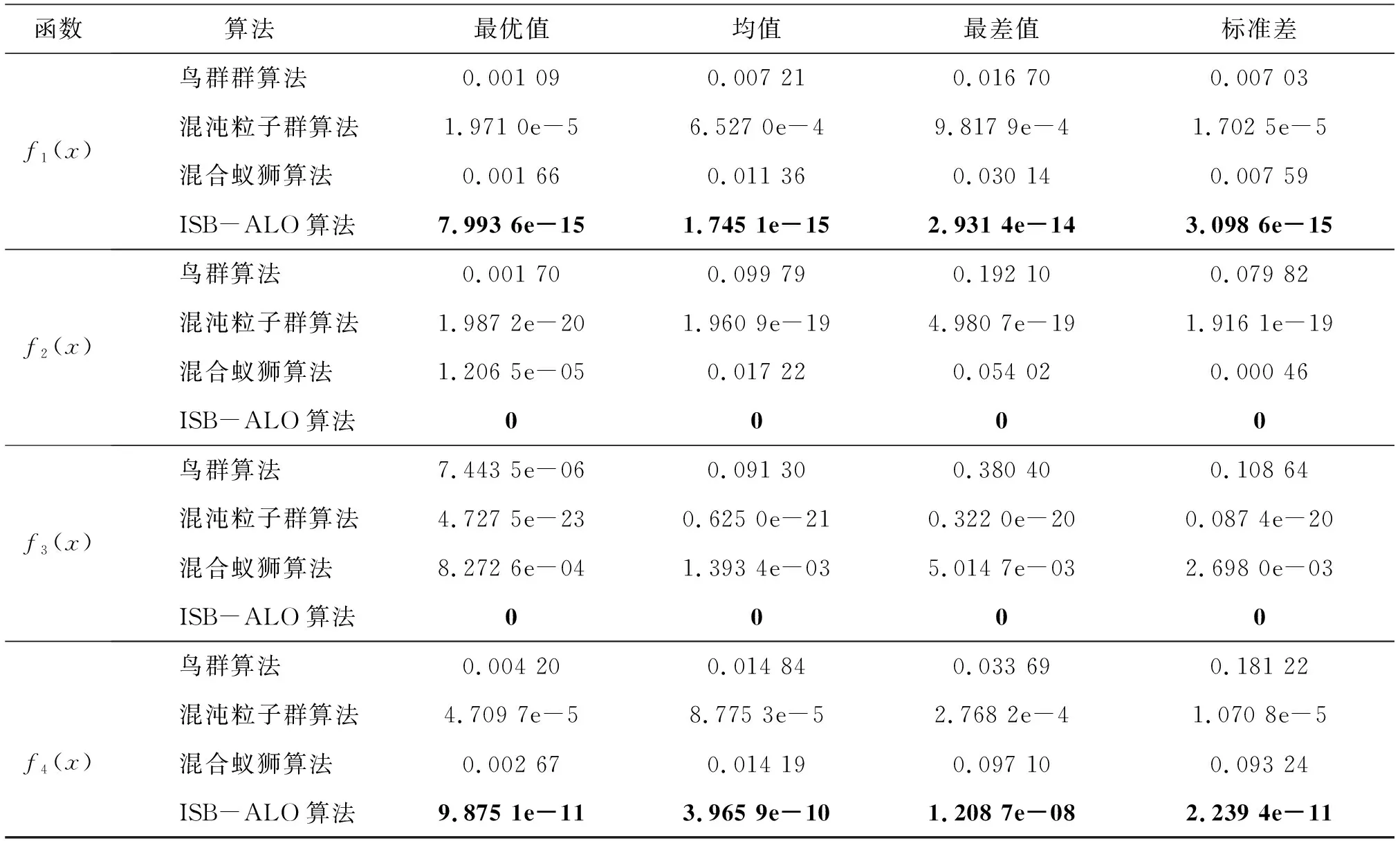
表5 测试函数结果对比
3.2 BN结构学习结果验证
为了证明ISB-ALO能够有效提高BN结构学习的准确率,分别在采样100、500、1 000、3 000组的数据下,以标准的animal网络为背景,通过Matlab仿真,将该算法与混合蚁狮算法、鸟群算法、混沌粒子群算法的结构学习效果进行对比,为保证实验结果的准确度,将每组数据独立运行50次取平均值记录,各算法对比结果见表6,表中加粗字体为最优值。
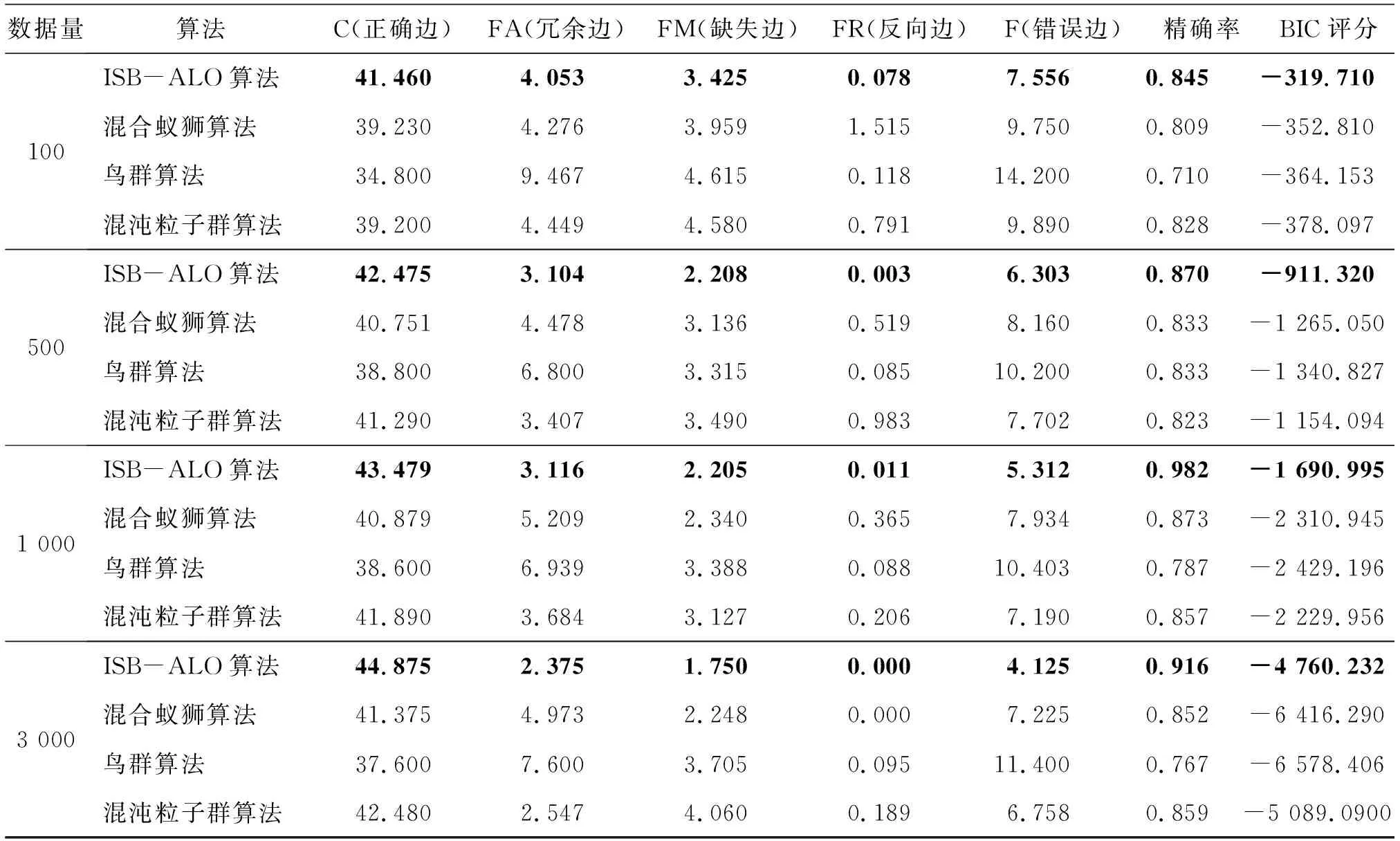
表6 BN结构实验结果对比
根据表6的实验数据,将各算法的BN结构指标——精确率、错误边以及BIC评分进行详细对比,结果见图5~7。
由图5可知,各数据量下,ISB-ALO算法的精确率均高于其他算法,且随数据量的增加呈现平缓上升的趋势,与混合蚁狮算法、鸟群算法、混沌粒子群算法相比,精确率的平均值分别提高了7.20%、16.97%、6.21%,这是因为对sigmoid函数的改进充分利用了有限数据,使结构学习的精确率得到提升,弥补了数据量不足的缺点。
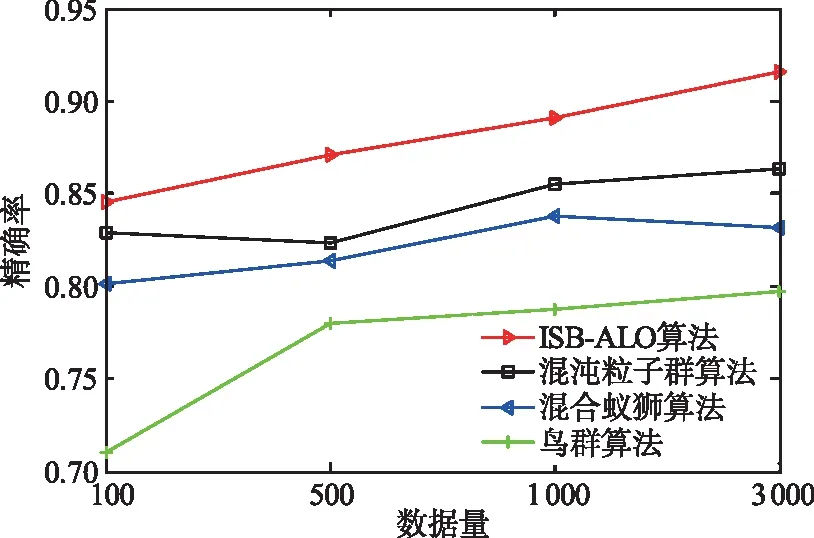
图5 各算法精确率对比
由图6可知,ISB-ALO算法的错误边都少于其他算法,且错误边数量随数据量线性递减,与混合蚁狮算法、鸟群算法以及混沌粒子群算法相比,错误边平均值分别减少了30.49%、49.34%、26.13%,这是由于算法迭代中互信息的约束,降低了错误迭代的概率,使得BN结构的错误边有所减少。
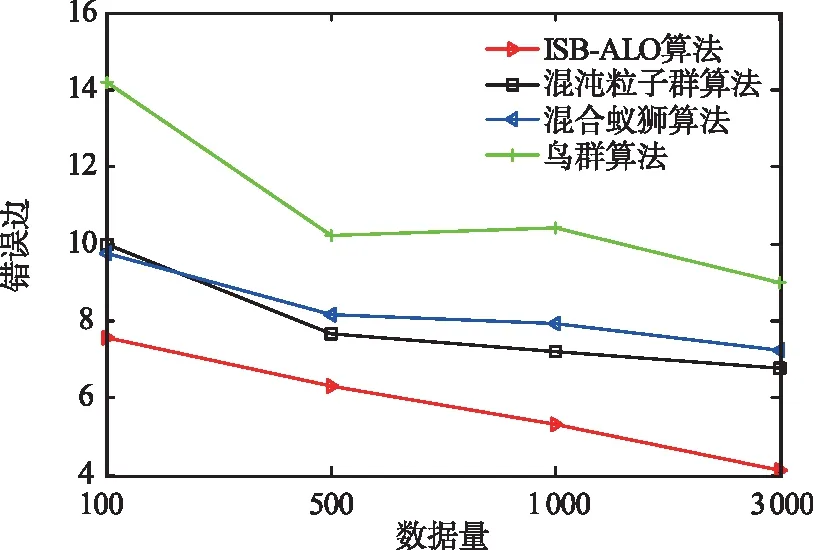
图6 各算法错误边对比
由图7可知,ISB-ALO算法的BIC评分相较其他算法均有所提高,且在数据量较小时就体现出明显的优势,与混合蚁狮算法、鸟群算法、混沌粒子群算法相比,BIC评分平均值分别提高了615.973,756.865,233.302。由此可见,ISB-ALO算法的学习结果在不同数据量,尤其是小数据集下均能保持较高的准确性,BN结构更接近标准的animal网络。
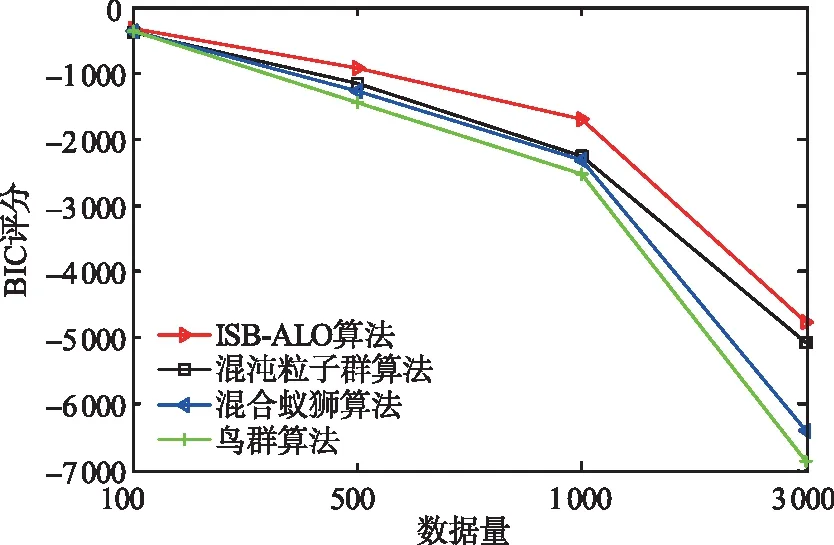
图7 各算法BIC评分对比
为验证算法的收敛性能,将ISB-ALO算法与混合蚁狮算法、鸟群算法以及混沌粒子群算法在小数据集下分别迭代50次的收敛曲线进行对比,见图8。
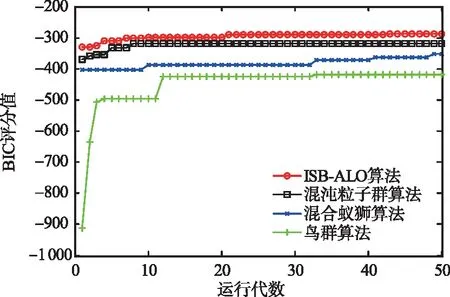
(a)数据量100
由图8可知,在数据量为100、500、1 000时,鸟群算法、混合蚁狮算法以及混沌粒子群算法的平均收敛代数分别为28、46、25,而ISB-ALO算法仅需16次迭代就能收敛到最优值,说明该算法结合BBO机制后能快速跳出局部最优。在最初迭代时ISB-ALO算法的BIC评分就高于其他算法,这是由于互信息对初始结构的约束,且在整个收敛过程中BIC评分都高于其他算法,进一步证明了改进方法在小数据集下具有较高的学习效率。
4 结语
针对BN结构学习算法易陷入局部最优以及数据利用不充分的缺陷,本文提出了基于改进蚁狮优化的贝叶斯网络结构学习算法。一方面由于对sigmoid函数的改进,充分利用了有限数据,提高了结构学习的精确率;另一方面结合BBO机制提出的3个算子,使结构学习算法易跳出局部最优,进一步提升了搜索效率和BN结构的准确度。仿真结果证明本文算法在小数据集下BN结构学习的可行性以及对蚁狮算法改进的有效性。
此外,BN结构学习在与智能算法结合时会增加总体的仿真时间,从而降低学习效率,因此,减少时间开销,进一步提高BN结构学习的效率也是值得考虑的问题。

