提炼解题模型 提高解题技能

文／李进

三角形是中考必考图形。从问题中提炼模型，可以帮助我们分析解题，也是我们需要培养的重要技能之一。下面，我们对一道中考题进行分析，解读掌握模型的重要性。

（2022·湖南湘潭）在△ABC中，∠BAC=90°，AB=AC，直线l经过点A，过点B、C分别作l的垂线，垂足分别为点D、E。

图1

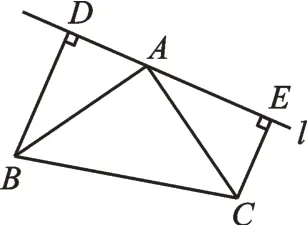
图2

图3

（1）特例体验：如图1，若直线l∥BC，AB=AC=，分别求出线段BD、CE和DE的长；

（2）规律探究：

（Ⅰ）如图2，若直线l从图1 状态开始绕点A旋转α（0＜α＜45°），请探究线段BD、CE和DE的数量关系并说明理由；

（3）根据题意，我们容易证明△ABD∽△FBA，由此可得出BF的长，从而根据S△BFC=S△ABC-S△ABF得出结论。

2016年，美国疼痛学会、美国麻醉科医师学会和美国区域阻滞与疼痛医学学会联合发布了术后疼痛管理指南[1]，提出多模式镇痛作为围术期疼痛管理的核心。该指南在术后疼痛管理的多方面均作出了更新，要求麻醉科医师进一步改进临床行为，将单一的以术后镇痛药物作为疼痛管理的方式改进为基于“药物干预-局部阻滞技术-区域阻滞技术-椎管内镇痛-非药物手段干预”等技术手段的多模式镇痛，以不断完善术后镇痛的质量和疗效。针对中国的现状，主要有以下三点需要作出改进。

【分析】（1）容易证明△ABD和△ACE均是等腰直角三角形，然后根据等腰直角三角形的三边关系可得到BD、CE和DE的长。

（Ⅱ）容易证明∠ABD=∠CAE，由“AAS”即可得出△ABD≌△CAE，从而解答；

（3）尝试应用：在图3 中，延长线段BD交线段AC于点F，若CE=3，DE=1，求S△BFC。

（2）（Ⅰ）容易证明∠ABD=∠CAE，由“AAS”即可得出△ABD≌△CAE，从而解答；

（Ⅱ）如图3，若直线l从图1 状态开始绕点A顺时针旋转α（45°＜α＜90°），与线段BC相交于点H，请再探线段BD、CE和DE的数量关系并说明理由；

解：（1）在△ABC中，∠BAC=90°，AB=AC，

2.2.2治理原理采用工程措施修整侵蚀沟沟体，布设植物防护体系，恢复生态，稳固沟体。当侵蚀沟坡度较大或者沟体不适宜种植植物时，采取工程措施(削坡、鱼鳞坑、水平阶等)对侵蚀沟做沟形修饰，从而确保植物措施的实施、成活与生长，发挥固沟导水作用。

正是丰收时节的一天，我在路上遇到二叔，想到他家种了四亩葡萄，便笑着问：“二叔，今年数钱都数到手酸了吧？”我本想二叔一定会微笑着谦虚地说“哪里哪里，除了锅巴不剩饭”，可他苦笑了一下，叹口气说：“白苦一年不说，还倒贴黄瓜二条，贴老本了。”

在Rt△ADB中，∠ABD+∠BAD=90°。

匮乏组织化的机构是一个非常现实的问题。但是，中国的家庭承担了主要责任，而且几乎每个人在相当大程度上都拥有自己的“亲朋好友”。通过慈善基金和一般性捐赠，我们建立了一个救助备用基金，以便为那些亟需金钱的患者提供救助。许多病人不需要或只需要极少量的金钱，他们迫切需要的是医疗人员的专业知识，迫切需要知道如何让病人和他们的家人获得所需医疗信息的方式，迫切需要知道社区能够提供什么，迫切需要知道他们能够做什么和他们应该怎样做。

在△ABD和△CAE中，

（2）（Ⅰ）DE=BD+CE。理由如下：

1962年1月天津市五一表厂更名为“天津手表厂”，同年底工厂迁入复康路新址，其工装设备、生产规模和产品数量都得到了提升。早在1961年3月天津表厂技术人员张凤鸣、温淑杰、江达生等设计出一款带秒表测时机构的计时码表机心，表厂定型为“ST3型”。到1963年12月表厂试制出该机心航空计时表样机32只，并通过轻工部和部队主管部门专家组的鉴定，该表定名为“304”航空表，是我国第一款装备空军飞行员的航空计时表（图09）。

（Ⅱ）DE=BD-CE。理由如下：

在Rt△ADB中，∠ABD+∠BAD=90°。

在△ABD和△CAE中，

（3）由（2）可知，∠ABD=∠CAE，DE=AEAD=BD-CE。

教师在开展中长跑运动时，单一的以训练为主，没有合适的方式方法，无法引导学生去摆脱抵触情绪，所以学生的畏难心理日益严重，对中长跑运动的兴趣也直线下降。

【点评】本题是一道三角形综合题，考查了直角三角形的性质、全等三角形的判定与性质、相似三角形的性质与判定、三角形的面积等知识。

在解答本题时，我们主要运用了“一线三等角”模型：指有三个等角的顶点在同一直线上的构图。“一线三等角”模型中的三角形分在直线同侧和异侧两类，角分直角、锐角、钝角三种，如图4。在这样的模型中，我们容易找到一对全等三角形或一对相似三角形，即△ABC与△CDE全等或△ABC与△CDE相似，从而为下一步解决问题提供思路。

图4