从中考题透视函数的广泛应用性

文／陈丽

函数应用题的考查形式多样，笔者以为可大致分为以下三类：生活情境类函数问题、跨学科情境类函数问题、数学情境类函数问题。

一、链接生活，品函数应用

例1（2022·山东滨州）某种商品每件的进价为10 元，若每件按20 元的价格销售，则每月能卖出360 件；若每件按30 元的价格销售，则每月能卖出60 件。假定每月的销售件数y是销售价格x（单位：元）的一次函数。

（1）求y关于x的一次函数表达式；

（2）当销售价格定为多少元时，每月获得的利润最大？并求此最大利润。

【解析】（1）题目已明确函数类型，根据所给条件用待定系数法易求得一次函数表达式为y=-30x+960（10≤x≤32）。（2）该题是典型的利用二次函数求最值问题。根据问题中的数量关系，即每月总利润=每件利润×每月的销售件数，可得每月获得的利润w=（-30x+960）（x-10），配方得w=-30（x-21）2+3630，根据二次函数性质以及自变量取值范围易知，当销售价格x定为21元时，每月获得的利润最大，最大利润为3630元。

【点评】对于生活情境类题型，同学们需仔细审题，厘清题目中各数量之间的关系，再构建函数表达式解决问题。同时，在平时的学习中，需不断累积生活经验，熟悉具体的生活情境，了解生活中常见数量关系，如：路程=速度×时间，工作总量=工作效率×工作时间，利息=本金×利率×期数等。在解题过程中还需注意结合生活实际考虑自变量的取值范围。

二、跨界合作，觅函数踪影

例2（2022·浙江台州）如图1，根据小孔成像的科学原理，当像距（小孔到像的距离）和物高（蜡烛火焰高度）不变时，火焰的像高y（单位：cm）是物距（小孔到蜡烛的距离）x（单位：cm）的反比例函数，当x=6时，y=2。

（1）求y关于x的函数表达式；

（2）若火焰的像高为3cm，求小孔到蜡烛的距离。

图1

【解析】（1）根据已知条件，用待定系数法易求得反比例函数表达式为。（2）把y=3代入函数表达式，得x=4，即小孔到蜡烛的距离为4cm。

【点评】此类题型属于跨学科情境类问题，是中考的一个新趋向。本题以物理学科知识为背景，可从小孔成像原理中挖掘数学问题。

三、数形结合，显函数魅力

例3（2022·江苏扬州）如图2是一块铁皮余料，将其放置在平面直角坐标系中，底部边缘AB在x轴上，且AB=8dm，外轮廓线是抛物线一部分，对称轴为y轴，高度OC=8dm。现计划将此余料进行切割：

（1）若切割成正方形，要求一边在底部边缘AB上且面积最大，求此正方形的面积；

（2）若切割成矩形，要求一边在底部边缘AB上且周长最大，求此矩形的周长；

（3）若切割成圆，判断能否切得半径为3dm的圆，请说明理由。

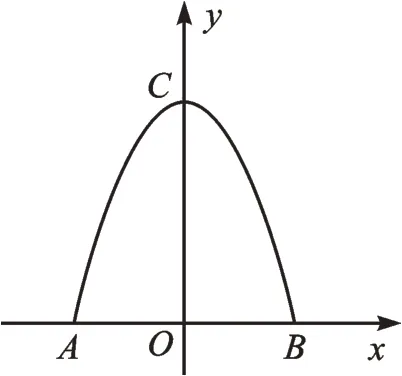
图2

图3

（2）如图4，设矩形落在AB上的点E的坐标为（n，0）（0＜n＜4），则可利用已求的二次函数表达式表示出点F的坐标，即可表示出矩形边FE的长度为，易求得矩形的周长C与n的函数表达式为C=-n2+4n+16，配方得C=-（n-2）2+20，根据二次函数性质以及自变量取值范围，得当n=2 时，矩形周长最长，最长为20dm。

图4

图5

【点评】本题虽然以生活实际为背景，但主要是数学内部知识即几何与函数相结合的一道综合题，考查了二次函数的基础知识，以及正方形、矩形、圆与二次函数图像的相关性质。此类问题的解决，除了需要熟练掌握各种几何图形的性质，准确提取问题的关键条件，结合相关知识转化问题、构建模型之外，还需要利用数形结合的方法来帮助解决问题。