“究错”，不犯错

文／肖文芳

我们在初中阶段主要学习了一次函数、二次函数、反比例函数三类常见函数，因其有综合性强、难度大等特点，在答题过程中有不少易错点。下面结合具体实例分析错因，希望能帮助大家在函数专题学习中，不犯或少犯错。

一、理解函数概念是远离错误的根本

例1下列四个图像中，不能表示函数图像的是（ ）。

【解析】这四个图像不是熟悉的三类函数图像，乍一看，似乎都错。函数概念的关键是“对于两个变量x、y，自变量x的每一个值，函数y都有唯一的值与它对应”，由此，选项A、B、C 都符合要求。对于选项D，自变量x取一个值，函数y存在两个值与其对应的情况，故选D。正确理解函数概念是解决函数问题的根本。

二、巧妙运用特殊点是少犯错的窍门

例2在同一平面直角坐标系中，一次函数y=ax+a2与y=a2x+a的图像可能是（ ）。

【解析】由一次函数概念可知a≠0。若a＞0，两条直线都经过第一、二、三象限，但没有选项符合题意。因此a＜0，则a2＞0，排除选项A、B。进一步观察函数表达式不难发现，当x=1 时，两个函数值都是a+a2，这表明两条直线都经过点（1，a+a2），故选D。本题以一次函数的图像及性质为依托，考查观察和推理能力。

三、善于运用函数图像是提高正确率的保障

例3已知点、C（2，c）都在关于x的二次函数y=mx2-2mx-2（m＞0）的图像上，则（ ）。

A.a＜b＜cB.b＜c＜a

C.c＜b＜aD.a＜c＜b

【解析】有些同学简单地认为y随x的增大而增大而误选A，或认为y随x的增大而减小而误选C。研究二次函数的增减性，要考虑它的对称轴，即直线，结合函数图像（如图1），不难看到A、B、C三点的相对位置，所以b＜c＜a，故选B。研究函数的增减性，我们要善于结合函数图像，在数形结合中化难为易。

图1

四、构造、利用函数是突破难点的“利器”

例4如图2，已知点A（1，2）、B（5，1），点P为线段AB上的一个动点，反比例函数y=的图像经过点P。当点P从点A运动至点B的过程中，k值不断变化，请求出k的最小值和最大值。

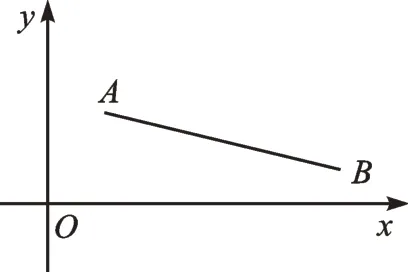
图2

同学们，只有深入理解各类函数的概念、图像及性质，善于数形结合、大胆建模、灵活推理，才能不犯错或少犯错，提高得分率。