无人水翼航行器纵向运动建模及控制研究

孙佳宇，刘增武，段富海，毛 翎

(1.大连理工大学 机械工程学院, 辽宁 大连 116024；2.大连测控技术研究所, 辽宁 大连 116013)

0 引 言

无人航行器具备隐蔽性好、体积小以及自主能力强等独特优势，可用于海面巡防、反潜、反水雷等任务，已成为海防领域不可或缺的重要力量[1]。现阶段国内外无人航行器已进入实用阶段，研究重心为如何提高其性能。将水翼应用于无人航行器以提升其整体性能已成为一个新的研究热点。近年来各种无人水翼航行器相继出现，如波浪能推进水面航行器[2]、两栖水翼航行器[3]、无人水翼船[4]等。

T-S 模糊模型是一种非常有效的非线性系统线性化方法[5]，现阶段已应用于船舶减摇[6]、动力定位船舶控制[7]、水翼船运动控制[8]等领域，可为无人水翼航行器的数学建模与姿态控制系统的设计提供借鉴。

最优控制中LQR 算法比较成熟，因此广泛应用于T-S 模糊模型的控制。但LQR 的参数多采用人工试凑的方法进行选取，效率低下且难以选取到最优参数。为改进选取参数的盲目性，可采用布谷鸟算法对LQR参数进行寻优。

本文首先介绍一种新型无人水翼航行器并建立其纵向运动非线性数学模型，利用T-S 模糊模型对非线性数学模型进行线性化；然后对T-S 模糊模型中各子系统设计LQR 控制器，并采用布谷鸟算法对LQR 控制器参数进行优化。最后，通过仿真验证在随机海浪干扰下所设计控制器的有效性。

1 无人水翼航行器整体结构及运行机理

无人水翼航行器结构如图1所示，其动力源为两电机带动螺旋桨转动在水中产生推力推动航行器前进。初始状态下仅航体漂浮在水面上，其余部分均浸没在水中，随着运行速度提高，水翼升力也随之变大，当达到一定速度后水翼升力可将航体抬出水面达到翼航状态。翼航状态下可通过调整前后水翼转动角度以改变前后水翼升力大小，进而可以调整航行器姿态。航行器姿态控制系统如图2 所示。

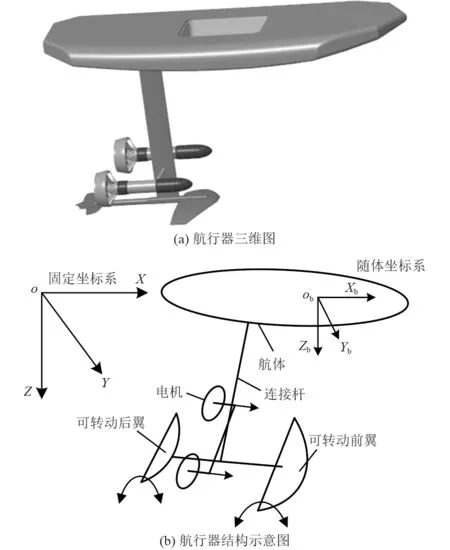
图1 无人水翼航行器示意图Fig.1 Schematic diagram of unmanned hydrofoil vehicle

图2 航行器姿态控制系统示意图Fig.2 Schematic diagram of vehicle attitude control system

2 无人水翼航行器纵向运动数学模型

2.1 非线性数学模型的建立

无人水翼航行器运行机理与水翼船相似，因此可借鉴文献[8]水翼船数学模型对其进行建模。考虑航行器纵倾和波浪对航行器运动的影响，忽略海流、海风等其他因素。翼航状态下航行器纵向受力如图3 所示。

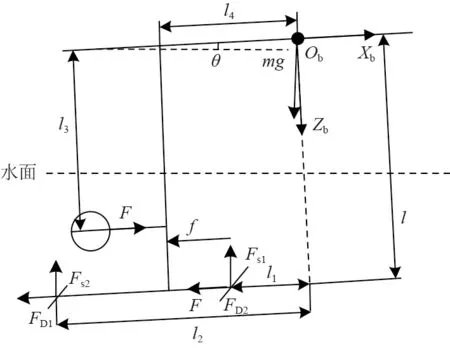
图3 翼航状态下航行器纵向受力示意图Fig.3 Longitudinal force diagram of vehicle under wing navigation

Fsi为前后水翼产生的升力与惯性力的合力(i=1 为前翼，i=2 为后翼)，即Fsi=Lfi+Fai。li为水翼距航行器重心距离。水翼升力Lfi的计算公式为：

式中：ρ为水密度，1 000 kg/m3；v为航行器运行速度；Si为水翼投影面积，Si=Libi；Li为水翼展长，bi为水翼弦长；Cfi为水翼升力系数，在文献[9]中有详细计算过程，水翼升力系数可近似看作与攻角成线性关系[10]。攻角计算公式为：

式中：αsi为水翼旋转角度，在±15°内变化；θ为纵摇角；ξ为航行器垂直于水平面升沉量；ζi为次波面海浪波形；α0i为水翼零升力攻角。

当航行器在水中运动时，会受到其周围流体作用的惯性力Fai，其计算公式为：

FDi为水翼阻力，其值远小于水翼升力[8]，所以忽略其在Zb轴方向分量，近似其方向与Xb轴平行，其计算公式为：

式中，CDi为水翼阻力系数，详细计算过程见文献[9]。

f为连接杆割划水面所产生的阻力，将连接杆抽象成一细长圆柱体，根据Morison 公式，作用在静水中匀速运动长度为dz的圆柱切片上的水平阻力大小为：

式中：D为圆柱直径，取为0.05m；Cd为阻力系数，取为1。连接杆水下浸没深度为h时的阻力大小为：

纵倾角小范围内变化时h≈l+ξ+l4θ，l4为连接杆至重心距离。

而阻力的力矩则可由下式计算：

设F为电机推力，匀速运动时与阻力大小相同，l3为电机推力力臂。在Zb方向利用牛顿第二定律并以Yb为转轴利用刚体定轴转动定律，可得到航行器翼航状态下纵向垂荡和纵摇运动数学模型：

无人水翼航行器结构参数如表1 所示。

表1 无人水翼航行器结构参数Tab.1 Structural parameters of unmanned hydrofoil vehicle

2.2 航行器T-S 模糊模型的建立

T-S 模糊模型的主要思想是将复杂非线性曲线用多条线段进行拟合，进而将非线性问题转化为多条小线段上的线性问题。航行器纵向运动T-S 模糊模型前提变量选取纵摇角θ，设航行器翼航状态时纵摇角范围为0°～4°，则前提变量分别取纵摇角θ为0°、2°、4°，由式(8) 可得各子系统参数如表2 所示。模糊规则如下：

在子系统1 工作点对式(8)进行线性化，即可得到如下参数：

其余A2，A3；B2，B3；H2，H3类似。

T-S 模糊模型的总输出为：

式中，wi为第i条规则关于纵倾角的隶属度函数，为三角形隶属函数，如图4 所示。

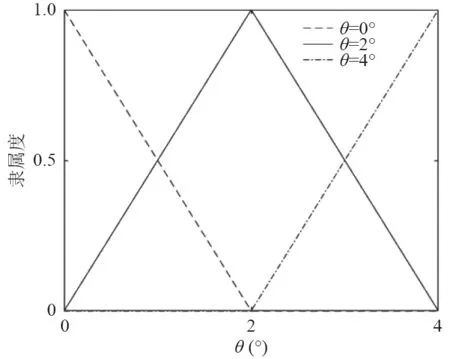
图4 隶属度函数Fig.4 Membership Function

并行分布补偿法(PDC)适用于解决基于T-S 模糊建模的非线性系统控制问题[11]。采用PDC 方法设计的T-S 模糊控制器为：

式中，Ki为各子系统反馈增益矩阵。

3 LQR 控制器设计及优化

3.1 LQR 控制器

LQR 算法核心是用最小输入代价实现对各个目标的有效控制，状态空间方程为：

LQR 控制就是要寻找一个最优控制矩阵K，即确定一个状态反馈控制率u(t)=Kx(t)，使得如式(13)所示的性能指标达到最小。

反馈增益矩阵为：

矩阵P可由黎卡堤方程求得：

LQR 控制器控制性能的好坏直接与Q矩阵与R矩阵的取值相关，因此Q矩阵与R矩阵的选取是LQR 控制器设计的核心内容。

3.2 布谷鸟算法

布谷鸟搜索（CS）算法是由Yang 和Deb 于2009 年提出的一种智能优算法[12]。CS 算法采用下式对下一代鸟巢位置进行更新：

CS 算法首先由式(16)对下一代鸟巢位置更新，如果适应度函数值优于上一代则更新鸟巢位置。位置更新后每个鸟巢的位置有Pa的概率会再次随机改变位置，然后保留测试值最好的一组鸟巢位置，记为。最后判断算法是否满足结束条件，若满足，则结束迭代寻优，输出全局最优值。

3.3 基于布谷鸟算法的LQR 控制器优化设计

利用CS 算法对LQR 控制器进行寻优。首先确定Q和R矩阵所需寻优参数的个数，确定CS 算法中搜索空间的维数和鸟巢坐标与各参数的对应关系，每个鸟巢即为各参数的集合体，本文设定Q矩阵形式为：

式中：q1和q3均取为0，仅调整q2和q4，R矩阵取为单位矩阵。

鸟巢的好坏由适应度函数所决定，采用时间误差积分准则（ITAE）作为适应度函数，以确保系统具有良好的动态性能[13]。CS 算法的目标就是找到一个最优鸟巢，然后将寻优后的参数代入Q矩阵得到最优Q矩阵，计算后得到最优状态反馈K矩阵。具体流程图如图5 所示。

图5 布谷鸟算法优化LQR 流程图Fig.5 LQR flow chart of cs algorithm optimization

4 仿真及结果分析

利用CS 算法对3 个子系统进行LQR 控制器参数整定，算法初始参数设置为：鸟巢数量为10、步长控制量α=1、发现概率Pa=0.25、变量取值下界为[0,0]、变量取值上界为[5 000,5 000]，迭代次数100 次，最终得到各子系统反馈增益矩阵为：

为检验CS 算法优化LQR 纵向姿态控制器的性能，加入随机海浪干扰，海浪参数为有义波高1 m，遭遇角120°，利用Matlab 2020b 软件编写程序，取纵摇角θ为1°，2°，3°三个工作点进行仿真。以升沉量误差Δξ和纵摇角误差Δθ作为评定纵向姿态控制器性能的指标，仿真结果如图6～图8 所示。

图6 纵摇角1°时控制效果Fig.6 Control effect at pitch angle of 1°

图7 纵摇角2°时控制效果Fig.7 Control effect at pitch angle of 2°

图8 纵摇角3°时控制效果Fig.8 Control effect at pitch angle of 3°

由仿真结果可见在随机海浪干扰下LQR 控制器对航行器纵向运动姿态具有良好的控制性能，升沉量误差Δξ和纵摇角误差Δθ均控制在小范围内，且利用CS 算法设计LQR 控制器不仅避免了人工试凑法的繁杂过程，控制效果也优于传统LQR 控制器。

5 结 语

本文提出一种新型无人水翼航行器，并以水翼船模型为参考对其进行纵向运动建模和T-S 模糊模型线性化。设计LQR 控制器，针对LQR 控制器采用人工试凑法调节参数效率低下的问题，利用布谷鸟算法对控制器进行优化。通过仿真验证了LQR 控制器对航行器在海浪干扰下的纵向姿态具有良好的控制效果，且经过布谷鸟算法优化后的LQR 控制器控制效果优于传统LQR 控制器。本文研究可为新型无人水翼航行器的实体样机设计提供理论依据，也可为其他种类航行器设计提供借鉴。