水循环与水资源合理配置模型(SWAM)Ⅰ:模型原理与构建

赵晶, 王涛, 毕彦杰, 韩宇平, 王培灵, 刘惊哲

(1.华北水利水电大学 水资源学院,河南 郑州 450046; 2.河南省黄河流域水资源节约集约利用重点实验室,河南 郑州 450046)

流域或区域水资源时空分布不均、水利工程设施不足、工程管理不善和社会经济快速发展产生的需水增加等,造成全域或局部地区出现了缺水和水生态环境恶化等一系列水资源问题。水资源配置是解决水资源问题的有效方式,是指应用各种方法和措施,保障未来社会经济发展的需水量、供水量在时间和空间上分配均衡,以满足生产、生活、生态环境3个方面的用水需求[1]。水资源配置实质上是一个多目标、多阶段、多主体的复杂决策问题。水资源配置系统涉及自然水循环系统、社会经济发展、人口、产业结构与布局、产品类型、技术水平、水资源条件等因素,是一个复杂的大系统,需应用模型开展研究[2]。水资源配置模型大致可分为模拟模型、优化模型和混合模型3类[3]。模拟模型一般依据节点的来水、供水、蓄水、回归水,按从上游到下游的顺序进行逐节点水量平衡计算[4]。该类模型较为简单,但一次只能模拟一个方案,当计算多种方案时需依据目标进行人工调节,进而比选、推选方案,存在不易快速取得最合理方案,且计算工作量较大的缺点。混合模型以模拟模型运算为基础,将运算过程中的人工比选方案进行自动化处理,缺点是运算繁琐、工作量大。优化模型根据设定的目标个数的多少分为单目标优化模型[5]和多目标优化模型[6]。两种优化模型均应用优化算法自动计算最优配置方案,优点是可以自动求得优化方案,缺点是计算时间稍长,且当以经济效益、社会效益为目标时,会增加复杂大系统的计算难度,但随着计算机技术与优化算法的发展,以上问题基本可以得到解决[7]。

水循环是水资源形成与演变的基础,是水资源配置的前提。已有学者开展了基于水循环模拟的水资源配置模型研究,如:赵勇等[8]开发了WACM(Water Allocation and Cycle Model)广义水资源合理配置模型其包括水资源合理配置、水循环模拟和水环境模拟3个模块;曾思栋等[9]开发了DTVGM-WEAR(Distributed Time Variant Gain Model-Water Evaluation Allocation and Regulation)分布式水资源配置模型;桑学锋等[10]研究构建了WAS(Water Allocation and Simulation Model)概念性半分布式水资源综合模拟与调配模型;JIANG Y等[11]建立了基于农业用水的灌溉水量优化配置模型;杨明智等[12]通过在改进的SWAT模型中嵌合水资源配置模块,开发了基于水循环的分布式水资源调配模型。以上研究大多采用单目标配置模型,仅少部分研究采用多目标配置模型,且多目标配置模型求解过程中往往通过人为赋予权重将多目标转化为单目标来求解[6,13],其计算结果易受到决策者的主观偏好影响[14]。此外,使用单一指标对多目标模型进行单目标转换,不能体现多个决策者的配置要求,也无法量化配置方案对多个维度的综合影响。为此,一些学者将各类优化算法引入到多目标优化模型的求解中,如:陈南祥等[15]引入了基于目标排序计算适应度的多目标遗传算法,通过反复迭代完成了水资源的多目标优化配置;黄显峰等[16]引入了多目标混沌优化算法来求解水资源多目标优化配置模型;田晶等[17]应用第2代非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm-II,NSGA-II)求解了汉江中下游地区的水资源多目标优化配置模型;郭萍等[18]应用遗传算法求解了非线性多目标水土资源配置模型的Pareto解集。此外,模拟退火遗传算法[19]、改进的类电磁学算法[20]、粒子群算法[21]、改进的鲸鱼算法[22]等也被应用于水资源配置模型的求解中,极大地提高了模型求解效率,为解决复杂水资源系统配置问题提供了新思路。

以往基于水循环模拟的水资源配置模型基本为松散耦合水循环模型,采用共用参数或数据传递的方式,耦合集总式水资源配置模型与水循环模型[12],其对人类活动下的用水过程与天然水文循环过程之间的相互影响反映不足;还有一部分模型将单目标或多目标转化为单目标求解,缺少多个目标之间的博弈过程,无法提供更多决策信息与多个目标之间的博弈信息。针对以上问题,本文构建了水资源模拟与多目标配置模型,通过设置水循环模块、多水源分质供水模块、需水模块和多目标配置模块,在时间、空间和用户3个层面上实现了从水源到用户的精细化水量分配;引入遗传算法NSGA-II求解了模型;基于Python语言开发了模型,设计了流场化的操作界面,实现了在一张图上完成水循环模拟与水资源调配的一体化模拟,并自动生成可视化图表与配置方案。

1 模型框架

水循环与水资源合理配置模型(Simulation Water-cycle and Allocation Model,SWAM)是基于水循环模拟模型的多目标均衡最优,且满足各种约束条件和系统运行规则的水量合理配置模型。模型的主要功能模块包括水循环模块、多水源分质供水模块、需水模块和多目标配置模块。水循环模块为多水源分质供水模块提供科学的可供水量;在多目标配置模块计算完水资源配置方案后,筛选出推荐方案,再进行水循环运算,直至结果合理、满意为止。SWAM基于Python语言在PyCharm集成环境下完成开发,其框架图如图1所示。

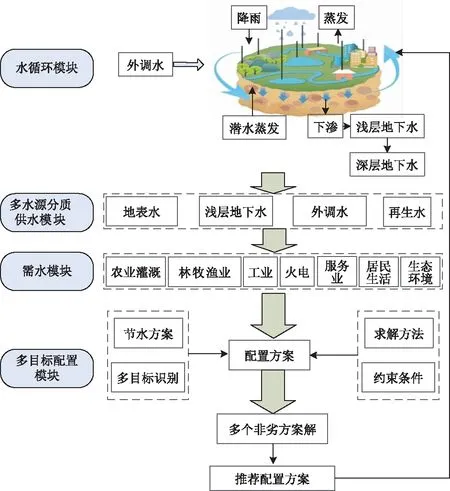
图1 模型框架图

2 模型原理与结构

2.1 水循环模块

水循环模块整体在网格新安江模型的基础上进行改进。模型的蒸散发部分采用三层蒸发模式,以考虑土壤湿度垂向分布异质性。产流部分采用新安江模型的蓄满产流方法计算。汇流部分:对于网格单元上的壤中流和地下径流均采用单位线法计算网格出流,并根据网格间的汇流演算次序依次叠加,直至流域出口;对于网格单元上的地表径流,不进行网格间的汇流演算,直接叠加至流域出口。在流域出口处,采用滞后演算法得到模拟出的日径流出流过程。

在模型参数确定方面,叶面积指数(LAI)根据每个网格单元的土壤类型确定;张力水容量(WM)、上层张力水容量(WUM)、下层张力水容量(WLM)、壤中流出流系数(KI)、自由水蓄水容量(SM)等参数根据其物理意义与土壤类型及植被覆盖之间建立的关系进行求解。由于河网水流消退系数(CS)与河网汇流滞时(L)反映的是整个流域河网的调蓄能力,因此采用集总式考虑;蒸散发折算系数(K)、河道汇流的马斯京根法系数(XE)、壤中流消退系数(CI)等参数,假设其在空间分布上是均匀的,采用流域统一赋值法[23]。

新安江模型应用于灌区时需要进行渠系引排水过程模拟。该模块通过设置一条引水干渠,从支渠引水节点位置,自上而下,逐个节点进行引水模拟,将水量从支渠分配到各个水循环单元。工业及生活取用水,根据实际调查统计情况与规划资料,进行流域每个水循环单元的生活与工业取水、排水计算。

模块对水利工程的模拟思路是:将各类水利工程概化为流域计算河网上的节点,通过一定的规则和要求来计算节点的水量平衡。

2.2 多水源分质供水模块

可供水量和各水源的取水控制量等约束条件来自区域最严格水资源管理用水总量控制红线和水循环模块的输出。实际取水量取决于计算单元的需水量和取水水源(如河道、水库、地下含水层等)的可供水量。

2.2.1 地表水(含外调水)供水

地表水(含外调水)的可供水量取决于水源的可利用水量、取水工程(如引水渠道、供水管道、机井等)的供水能力和水源(包括本地地表水与外调水)的取水控制红线等约束条件。取水量计算公式见式(1):

(1)

2.2.2 水库供水

水库库容计算由上一时段末库容和本时段水库上游来水、库面蒸发、水库渗漏和水库供水共同决定。水库水量平衡方程见式(2):

(2)

水库群调度遵循自上游到下游依次蓄水、供水计算的顺序,供水水量按照优先顺序供给指定的用水户。假设用水户的优先级为生活>工业>生态>农业,则第k个水库可供水量可表示为:

(3)

其中,

(4)

2.2.3 地下水供水

地下水补给量(来自水循环模块)和可开采量以各区域允许开采量为开采上限,可开采量(GR)可以在年内滚动提取,但不能跨年度累积。

2.2.4 再生水供水

随着水资源短缺问题日益突出,将非常规水源纳入供水体系势在必行。目前,我国对于非常规水资源的利用仍处于起步阶段,非常规水资源纳入水资源配置一般用于生态、农业、工业等[24],其为实现分质供水奠定了基础。本模型设定再生水用水户包括工业、生态、农业。再生水供水量的计算式为:

(5)

其中,

XZi=Wli(1-Ci)(1-HCi)。

(6)

式中:Qz为再生水供水量,万m3;XZi为第i个用水户的回归水量,万m3;R为再生水回用率,%;Wli为第i个用水户的用水量,万m3;Ci为第i个用水户的耗水率,%;HCi为第i个用水户漏损等其他耗水率,%。

2.3 需水模块

2.3.1 社会经济发展数据

该模型应输入现状年社会经济数据与规划水平年增速数据。社会经济数据包括:常住人口(农村、城镇)、大牲畜、小牲畜、工业、建筑业、服务业、作物(小麦、玉米、水稻、经济作物)种植面积、设计灌溉面积、林草地面积、渔业面积与GDP等。社会经济规划水平年增速数据包括:人口增速、GDP增速、产业结构变化率、作物种植面积变化率等。其中,现状年社会经济数据参考第七次人口普查、统计年鉴、水资源公报等;规划水平年增速数据参考区域/城市总体规划、国民经济和社会发展第十四个五年规划和2035年远景目标、工业发展“十四五”规划、农业发展“十四五”规划、水利发展“十四五”规划、环境保护“十四五”规划等。

2.3.2 需水量计算

1)农业需水量。其为农田灌溉需水量、林地需水量、草地需水量、渔业需水量之和,计算公式为:

DWT=DWA+DWF+DWS+DWY。

(7)

其中,

(8)

(9)

(10)

(11)

2)牲畜需水量。其预测模型为:

(12)

3)工业需水量。其计算公式为:

(13)

4)服务业与建筑业需水量。其计算方法与工业需水量的类似,分别用DWE、DWB表示。

5)生活需水量。其计算式为:

(14)

6)生态环境需水量。其分为河道内和河道外两种情况。河道外生态环境需水量DWe采用人均生态环境需水量乘以人口数进行计算;河道内生态环境需水量采用Tennant法进行计算。河道内的最小生态流量一般取多年平均流量的10%～20%,河道内生态环境需水量在水资源配置模型计算前应从可供水量中扣除。

2.3.3 节水情景设置

需水模块设置不节水、一般节水、深度节水3种节水情景。不节水情景指采用现状用水水平;一般节水情景指在现状节水水平和相应节水措施的基础上,基本保持现有节水投入力度,并考虑2000年以来用水定额和用水量的变化趋势所确定的节水模式;深度节水情景指实施更加严格的强化节水措施,着力调整产业结构,加大节水投资力度,可根据地方“十四五”水利发展规划、节水型社会建设规划、节水行动方案、水资源刚性约束值指标等综合确定。

2.4 多目标配置模块

2.4.1 目标函数

本模块设置3个目标:经济目标、社会目标与水量目标。经济目标通过区域经济效益最大来体现,社会目标以缺水引起的粮食减产量最小来体现,水量目标以缺水量最小来体现。

1)水量目标。其目标函数为:

minS=DWT+DWC+DWG+DWE+DWR+

DWB+DWe-SP-GR-Wl-Qz。

(15)

式中S为缺水量,万m3。

2)社会目标。其目标函数为:

(16)

式中:QSg为粮食减产量,kg/km2;Yml为作物l在充分供水条件下的最大产量,kg/km2;Yal为作物l的实际产量,kg/km2。其中Yal的计算采用Jensen模型(相乘模型),以各生育阶段腾发量为变量来模拟不同生育阶段水分亏缺对农作物最终产量的定量影响[25-26],其数学表达式为:

(17)

其中,

(18)

(19)

(20)

(21)

(22)

3)经济目标。其以经济效益最大来体现,对应于缺水引起的经济损失最小。目标函数为:

minZ=Vg+CI+CS。

(23)

式中Vg、CI、CS分别为农业、工业、服务业的经济损失值,亿元。

其中,农业经济损失值的计算式为:

Vg=(Ym-Ya)P。

(24)

式中P为价格,元/kg。

产业因缺水引起的工业和服务业的经济损失计算需先确定用水效益函数。该函数一般具有绝对效益随用水量递增、边际效益随用水量递减的特点[27]。本文引入广泛应用于经济学领域的效用函数——双曲绝对风险厌恶函数(Hyperbolic Absolute Risk Aversion,HARA)[28],表征用水量与经济效益之间的定量关系。HARA函数具有连续性,在定义的区域内是可导且严格递增的凹函数,具有单调递增和边际效益递减的特点。HARA函数的一般表达式为:

(25)

式中:α、β、γ均为系数,可通过调整其取值表征不同的效益函数;Wi为第i类产业的实际供水量;U(·)为用水效益函数。

缺水损失及缺水量之间具有函数关系,将缺水量Si=Ni-Wi(需水量-供水量)整理后代入式(25)即可求得缺水损失以及缺水量之间的函数关系:

(26)

式中:C(·)为缺水损失函数;P为不缺水时的总产值,亿元。

式(26)中,系数γ是小于1的常数,γ越小用水效益函数曲线越陡、边际效益递减趋势越显著;γ越大用水效益函数曲线越接近直线。根据文献[29],令γ=0.5,式(26)可进一步简化为:

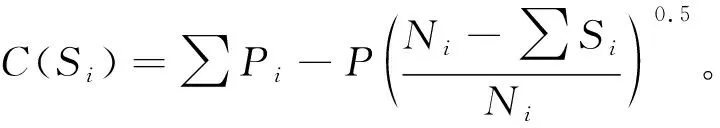
(27)

式中:0≤Si≤Ni;∑Si=Sa;Sa为行业总缺水量。

2.4.2 约束条件

1)生活用水优先保障。其约束条件为:

SRj≥NRj。

(28)

式中:SRj为第j个计算单元内居民生活供水量,L/(人·d);NRj为第j个计算单元内居民生活最低用水定额,L/(人·d)。

2)地下水供水量应满足地下水资源可供水量。其约束条件为:

GR≤NDG。

(29)

式中:GR为地下水供水量,万m3;NDG为“三条红线”约束下地下水可供水量,万m3。

3)重要生态保护要求。如河道流量应满足河道生态基流约束条件:

Qer,t≥QSer,t。

(30)

式中:Qer,t为河道r在t时段的流量,m3/s;QSer,t为河道r在t时段的最小生态用水量,即河道生态基流量,m3/s。

此外,水库最小下泄流量应满足如下约束条件:

(31)

4)输水节点流量限制。其约束条件为:

WFi≤Qsi。

(32)

式中:WFi为第i地区连通管道的输水流量,m3/s;Qsi为第i地区连通管道的设计输水能力,m3/s。

5)水库库容限制。其约束条件为:

(33)

其中,

(34)

6)非负约束条件,即模型中所有的决策变量均大于等于零。

(35)

若用缺水率代替收入,基尼系数越小,则缺水差异程度越低。因此,各配置单元的社会公平性约束可表示为:

(36)

2.5 信息的分解与聚合

2.5.1 信息分解

信息分解是指国民经济需水数据从大时空尺度向小时空尺度的分解。我国经济社会用水数据与供用水数据多以行政区为单位进行统计,水资源配置也多以行政区为配置单元。为便于数据收集与输入,模型以行政区为单位进行数据输入,再根据行政区内城市、乡镇以及农村的分布和面积大小、单位面积用水量数据进行分解,并展布到计算单元上。展布数据包括农业用水、生活用水、工业用水、服务业用水以及畜禽养殖用水等。

2.5.2 信息聚合

信息聚合是指水源供水与用户用水的衔接计算。水源供水计算是水资源配置模型与水循环模块耦合的一个重要环节。由于计算单元内有多种水源,将不同计算单元的各种水源汇总,以便于分水源进行用水总量控制。对不同计算单元属于同一行政区的各水源进行汇总,以便于各行政区分水源进行用水总量控制。对不同计算单元属于同一行政区水文单元的各种水源汇总,将数据传递给水循环模型的对应水源分质供水模块,参与水循环模拟。

2.6 计算单元划分

本文采用基于“行政区—子流域”多元属性的嵌套式坡面离散方法进行计算单元划分。首先,划分各行政区边界;其次,提取流域河网,划分天然子流域,从而划分出计算单元,即每一个计算单元都具有行政区属性、流域属性;最后,设置行政区和水文计算单元的映射关系,便于信息的分解与聚合。

2.7 水资源配置系统网络图绘制与拓扑关系构建

2.7.1 水资源配置系统网络图绘制

根据研究区的特征,选择大型、中型或者小型水库,取水口,引调水工程等作为水资源配置系统网络图绘制的基本工程节点;结合研究区水系分布特征,设置控制性节点/断面;根据各类工程、计算单元、水源的传输关系及水力联系,将计算单元内的用水户与供水节点/断面、排水节点/断面通过概化的输水河渠道连接,得到水资源配置系统网络图。

节点通常包括水源节点、用水单元节点、交汇节点、渠道(河道)。①水源节点一般包括水库(包括外调水水库)、地下水取水点、回用水源等。水库直接体现在水资源配置系统网络图中,地下水取水点和回用水源可概化到每个计算单元中。②用水单元节点一般为一个行政区或水资源分区套行政区。③交汇节点设置在汇流节点和进行水量分配的分水节水处,若有重要的湿地,将其单独作为汇水节点处理。④水资源配置系统网络图中连接各水源、各节点与各用水单元之间的纽带可概化为渠道(河道),如地表水供水渠道(河道)、外调水供水渠道、退水渠道。

水资源配置系统网络图应全面反映各用水户需求,各水源供给与排泄间的关系,以此作为水资源供需平衡计算的基础。

2.7.2 拓扑关系构建

每一个计算单元既是水循环模型的水文模拟单元,又是水资源配置模型的基本配置单元。建立水资源配置模型计算单元与水文模型计算单元之间的空间拓扑关系,便于数据传递和配置结果的逐日展布,实现两个模型的紧密耦合。节点包括引提水节点、水库节点、行政区间控制断面节点、流域控制断面节点等。建立计算单元与节点拓扑关系、计算单元与用水户拓扑关系、计算单元与水库拓扑关系、水库与用水户拓扑关系、不同水源与用水户的拓扑关系。

各计算单元、节水节点、用水户、水源间拓扑关系通过关系数据来存储和管理,可直接输入到模型中,便于实现模型的通用性。

3 模型求解方法

水资源系统模拟与配置模型具有高维度、强耦合和不确定性等特征,属于多阶段、多目标、多维度决策问题,适合采用帕累托模型求解,其所得解集如图2所示。图2中,在多目标优化最优前沿面上的任何一点都是最优解,都被称为非劣解 (Pareto解),Pareto解代表了不同目标之间的权衡,可协调水资源分配过程中多个目标间的矛盾,并呈现目标间的博弈过程[30-31]。本文的多目标优化模块共有3个目标函数和多个约束条件,而传统的蚁群算法、遗传算法、粒子群算法在求解含复杂约束条件下的多目标模型时,易陷入局部最优且Pareto 解收敛效果较差。为得到更加合理的全局最优解,引入第二代非支配排序遗传算法(NSGA-II),利用良好分布的参考点维持种群的多样性,更好地处理多目标高维度问题。多目标配置模块的计算过程如图3所示,通过反复循环,直到Pareto最优前沿面稳定,求得最优解。SWAM模型基于Python语言编写相应的程序,计算得到水资源配置方案。

图2 Pareto解集

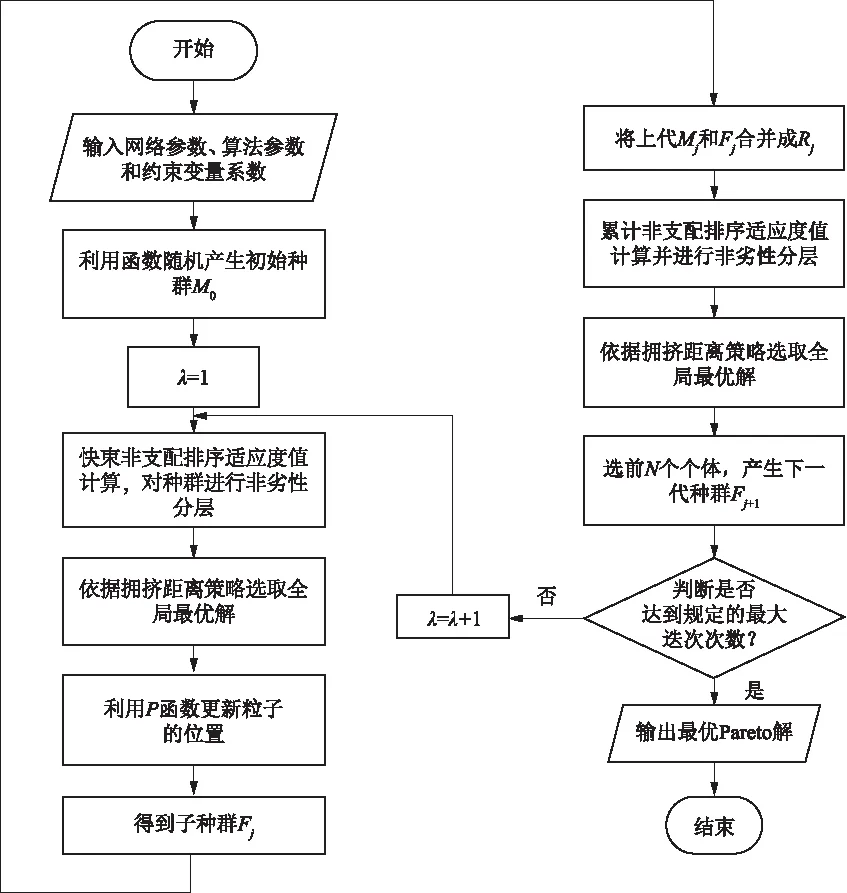
图3 NSGA-II计算流程

4 模型特色

4.1 双向耦合方法

根据水循环模块和水资源配置计算过程中的数据使用情况,两者的数据交互可归结为:水循环模块为水资源配置计算提供径流性水资源量与地下水可开采量等,通过“时空聚合”方法整合出适合水资源配置的时空尺度输入数据,即水循环模块为多水源分质供水模块提供科学的可供水量。经水资源配置模型计算后,将配置方案下的水资源“供、用、耗、排”过程进行时空展布,即分解到水循环单元上, 并叠加上降雨等其他水循环模块所需的输入,驱动水循环模块计算,得出该配置方案下流域(区域)水循环变化规律。在实际运行中,要将水循环模块的计算结果反馈给水资源配置模型,并及时调整修正水资源配置条件,然后基于调整后的水资源配置条件再次进行水资源配置和水循环运算,直至结果合理、满意为止。

具体来说,就是在建立“自然—社会”拓扑结构的基础上,运行水循环模块,进行水循环过程的模拟,得到各节点及断面的每日入流量、各水文计算单元的每日径流过程、下渗量与土壤水蓄变量,然后通过信息聚合方法,得到水资源配置模型所需要的时空尺度数据。其中,需要对节点入流、水利工程入流进行时间尺度汇总。水循环模块计算所得的地下水蓄变过程以及与地表水交换过程也需要输入到水资源配置模型中计算地下水可供水量。

反之,水资源配置计算基于水循环模块提供的来水信息及需水信息,利用长系列法进行流域(区域)水资源供需平衡分析,以及每个配置计算单元的供水量、用水量、耗水量、排水量,以及各水库、河流、湖泊等与地下水利用的取水信息。对以上数据进行时空展布,将月尺度的配置方案展布到日尺度的水文计算单元中,同时将各水库、河流、湖泊等与地下水利用中的取水、调水过程信息展布到日尺度。

4.2 模型界面设计

按照水资源配置模型需求与用户操作习惯,将用户界面左侧部分设置为配置区域GIS图层及相关区域水情数据导航窗口,选择其下相应的目录后,可在中间界面查阅相应内容。前端界面基于Python语言开发并结合QGIS技术,采用开源GIS封装技术便于GIS成图与空间展示,实现与GIS深度交互;GUI部分利用PyQt5框架提供友好的图形化展示界面,模型界面如图4所示。

图4 模型界面

模型设计的操作界面直观、友善、可操作性强、简单易学;批量化数据输入与单点输入相结合;导航窗口式管理操作简便,用户根据提示输入数据,模型即可自动生成可视化报表与模型结果图,还可批量输出excel报表,便于用户直接查看模型结果。该模型实现了在一张图上完成水资源调配建模、自动输出配置方案的目标。

5 结语

针对目前基于水文模拟的水资源配置模型大多采用松散耦合方法,且解决的多为单目标优化的问题,本文构建了水循环与水资源合理配置模型(SWAM), 系统地描述了模型结构、构建过程、求解方法,设计了模型界面。模型主要的功能模块包括:水循环模块、多水源分质供水模块、需水模块、多目标配置模块。其中,水循环模块在网格新安江模型的基础上进行了改进,模型蒸散发部分采用三层蒸发模式计算,产流部分采用蓄满产流方法计算,壤中流和地下径流均采用新安江模型中线性水库的方法计算网格出流,并考虑了引水排水模拟与水利工程模拟。多水源分质供水模块包括地表水、水库蓄水、地下水、再生水供水过程。需水模块考虑了3种节水情景,分行业计算各行业需水量。多目标配置模块设置经济目标、社会目标与水量目标3个目标,约束条件包括:刚性约束条件与非刚性约束条件,并引入遗传算法求解了模型。

本文构建的SWAM模型实现了水循环与水资源配置一体化模拟分析,可在一张图上完成水资源调配建模、自动输出配置方案。可作为区域自然-人工水循环互馈模拟以及水资源精细化管理的支撑工具。为进一步展示模型的构建过程与功能,将在下篇文章中进行模型实例应用分析。