航空滤光片阵列多光谱图像条带预处理算法

李铜哨,孙文邦,黄心禹,章正宜,白新伟

(1.空军航空大学, 长春 130022; 2. 94691部队, 福建 龙岩 366200;3. 93307部队, 沈阳 110000; 4.陆军特种作战学院, 广州 510630)

0 引言

无人机成像是一种低空遥感技术,具有成本低、灵活性高和数据采集快等优点,已经成为遥感信息获取的重要手段[1-2]。随着无人机平台逐渐小型化发展,对高性能、小体积相机的需求增加[3]。其中,滤光片阵列多光谱相机因具有结构简单、体积小、稳定性高、对平台要求较低等特点被广泛应用于无人机多光谱遥感[4]。

滤光片阵列多光谱相机同一时刻获得的图像数据为多波段图像,需要通过图像裁剪与拼接才能得到大区域单波段图像。其中,图像裁剪是滤光片阵列多光谱图像数据处理的前提,直接关系到条带图像重叠率与拼接图像质量。由于不同相机成像时滤光片阵列安装位置差异与条带边缘光谱混叠现象,无法使用同一条带有效区域对滤光片阵列多光谱图像进行裁剪,一定程度上影响了多光谱图像数据的后期处理。

目前,多光谱图像处理技术研究相对较为成熟,如条带图像灰度差异校正[5-6]、图像拼接[7-8]和单波段图像配准[9-10]等处理技术,但从图像处理角度确定条带有效区域范围的研究较少。相对于航空无人机成像技术,低空无人机飞行速度慢,相邻时刻成像得到的滤光片阵列多光谱图像重叠率较高、光谱混叠范围相对较小,可直接从目视角度确定条带有效区域范围。此外,曹丛峰等[11]通过实验室内光学测试得到滤光片阵列多光谱图像各条带有效区域位置,该方法虽然较为精确,但实验要求较高且实时性较差。

因此,提出了一种基于图像行/列像素灰度的航空滤光片阵列多光谱图像条带预处理算法,用于确定各波段条带有效区域范围,裁剪后的单波段图像不存在光谱混叠,且能最大程度保持条带图像间重叠率。

1 滤光片阵列多光谱成像特点

滤光片阵列多光谱相机主要由镜头、滤光片阵列和面阵CCD探测器构成,其中,滤光片阵列是多光谱相机核心元件,一定程度上决定了成像质量。滤光片阵列放置在CCD探测器前面,通过滤光片上镀制的带通滤光膜将CCD探测器划分为若干个光谱带,每次曝光获得目标区域的多波段图像,如图1所示(图中显示为8个滤光片)。

图1 滤光片阵列多光谱相机成像原理Fig.1 Imaging principle of filter array multispectral camera

由于多光谱相机的多波段图像均是在同一阵面上成像,需要进行图像拼接才能够形成一幅单波段图像,条带图像裁切拼接过程如图2所示。

图2 滤光片阵列多光谱数据面阵处理Fig.2 Area array processing of filter array multispectral dataset

滤光片阵列中每个带通滤光膜只能通过一个谱段的图像,条带之间设有隔离带,确保不会相互干扰。但由于成像光束具有一定口径,相机成像时相邻条带滤光片存在部分光束交叠,导致CCD探测器对应区域是2个单色光混合而成,即波段混叠区域[12],如图3所示。

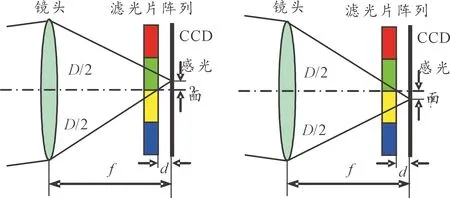
图3 CCD靶面混叠区域示意图Fig.3 Schematic diagram of CCD target surface mixing area

而波段混叠是采取滤光片阵列成像不可避免的现象,混叠区域与CCD探测器与滤光片阵列间的距离有关[13],一般在200个像元内,即每一条带上下100个像元为光谱混叠区域,如图4所示。

图4 波段混叠区域Fig.4 Band mixing area

从图4中可以看出,确定条带有效区域范围时,首先要去除条带中光谱混叠区域,否则会影响拼接后图像地物光谱信息的准确性。

此外,由于单波段条带图像为窄带宽图,条带重叠率较低,为了提高条带拼接质量,裁剪单波段条带图像时,应最大化保证条带图像重叠率。

2 滤光片阵列多光谱图像条带预处理

滤光片阵列多光谱图像条带预处理主要包括求取条带图像灰度极值点、计算光谱混叠范围和确定条带图像有效区域3个步骤。

2.1 求取条带图像灰度极值点

构建滤光片阵列多光谱图像条带模板首先要确定条带灰度极值点,即光谱混叠区域的中间位置。由于不同地物在同一波段下的光谱响应值不同,利用图像中一行/列像素确定条带灰度极值存在较大误差。此外,不同时刻获得的多光谱图像条带灰度极值点位置并不相同。

因此,为保证序列多光谱图像各条带对应的灰度极值点一致,选择对多幅滤光片阵列多光谱图像的行/列像素灰度均值进行求和,然后计算图像行/列像素灰度平均值,并以一维曲线进行显示,如图5所示。

图5 行/列像素灰度变化曲线Fig.5 Grey scale variation curve of row/column pixel

从图5中可以明显看出,相邻条带之间的光谱混叠区域像素的灰度变化曲线存在灰度极小值,可以看成光谱混叠区域的中间点。

一般情况下,滤光片阵列中间排列的滤光片等宽,而直接利用行/列像素灰度计算各条带灰度极值点无法保证条带有效区域宽度相同。因此,文中首先利用多光谱图像行/列像素灰度分别计算第1条带和第n条带的灰度极值点k1、kn-1,然后对灰度极值点k1、kn-1进行作差并进行均分处理,得到多光谱图像中间条带灰度极值点ki,如式(1)所示:

(1)

式中,n为多光谱图像波段数,i∈(2,n-2)。

2.2 确定光谱混叠范围

对于滤光片阵列多光谱相机而言,条带有效区域差别主要是滤光片安装位置变化,即条带图像灰度极值点存在偏差。随着镀膜技术的快速发展,采用同一种滤光片阵列获得的多光谱图像中条带光谱混叠范围大致相同。

因此,每种类型滤光片阵列只需确定一次多波段图像中条带光谱混叠区域范围f。其中f的宽度直接关系到条带图像的重叠率,对于重叠率较低的条带图像,要尽可能保留条带有效区域。

为了精确计算条带混叠区域宽度,利用条带图像中间区域灰度最小值分别计算条带图像左右两侧有效区域截止点,具体过程如下:

首先,设各条带光谱混叠范围为q个像素,利用灰度极值点ki计算条带灰度最小值mi,依次计算条带灰度极值点ki左侧和右侧条带图像有效区域截止点xi、yi。其中,xi、yi分别为条带图像灰度最小值mi与对应条带灰度变化曲线交点,如图6所示。

图6 条带灰度截止点Fig.6 Strip grey scale cut-off point

图6中红色点为条带中间区域灰度最小值,蓝色点为条带有效区域截止点。分别计算ki与xi、yi的差值fxi、fyi,取最大值作为序列图像两侧光谱混叠区域宽度f1、f2。

2.3 计算条带图像有效区域

利用条带图像光谱混叠区域宽度f1、f2和条带灰度极值点ki可计算出各条带有效区域范围,其中[ki-f1,ki+f2]为光谱混叠区,[ki-1+f2,ki-f1]为条带有效区域,如图7所示。

图7 条带有效区域Fig.7 Effective area of strip

以8波段滤光片阵列多光谱图像为例,条带图像光谱混叠沿垂直方向分布,设多光谱图像大小为r行c列,则各波段有效区域顶点坐标如表1所示。

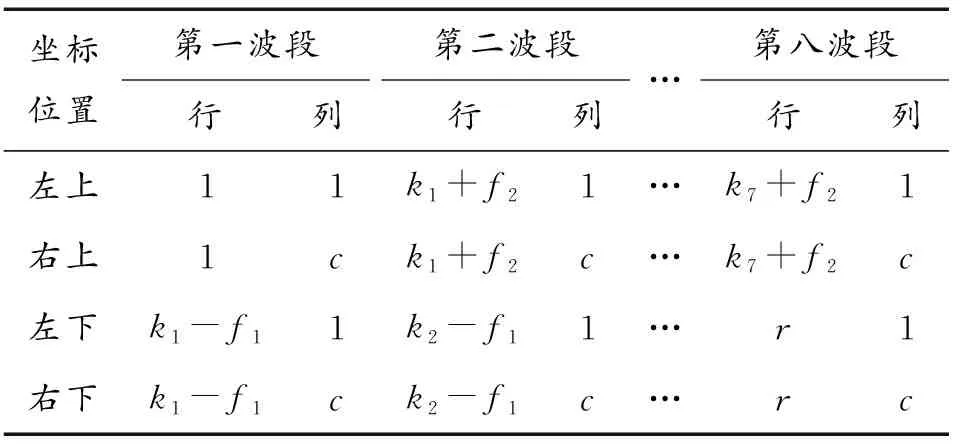
表1 各波段有效区域顶点坐标Table 1 Coordinates of effective area vertices in each band

为便于图像后期处理,可按照波段条带有效坐标构建条带图像模板,如图8所示。通过将图像模板与原始图像相乘得到不包含光谱混叠的多条带图像。

图8 各条带有效区域模板Fig.8 Template of the effective area for each strip

3 实验与分析

为了验证本文提出的滤光片阵列多光谱图像条带预处理算法的可行性,采用某型航拍无人机滤光片阵列多光谱相机拍摄的2组多光谱图像进行实验验证,其中,实验图像大小为4 008像素×5 100像素,如图9所示。

图9 实验图像Fig.9 Experimental images

以数据1为例,条带局部放大图如图10所示,可以看出,相邻条带之间存在明显的波段混叠。

图10 条带混叠区域Fig.10 Strip mixing area

对2组实验图像分别计算行像素灰度均值,并以一维曲线进行显示,如图11所示。

图11 图像行像素灰度变化曲线Fig.11 Image row pixel grayscale change curve

可以看出,2组实验图像的条带灰度极值点位置并不相同,同一条带有效区域位置存在差异,且第2波段光谱混叠范围较小。

为了精确得到条带有效区域范围,利用各行像素灰度均值分别计算实验图像中条带灰度极值点k7和k1,并依次得到中间条带灰度极值点k2、k3、k4、k5、k6。由于第2波段光谱混叠范围较小且灰度值较低,可不考虑第2波段光谱混叠区域。然后根据条带图像最低点计算条带图像有效区域截止点,得到各条带光谱混叠区域范围。如表2所示。

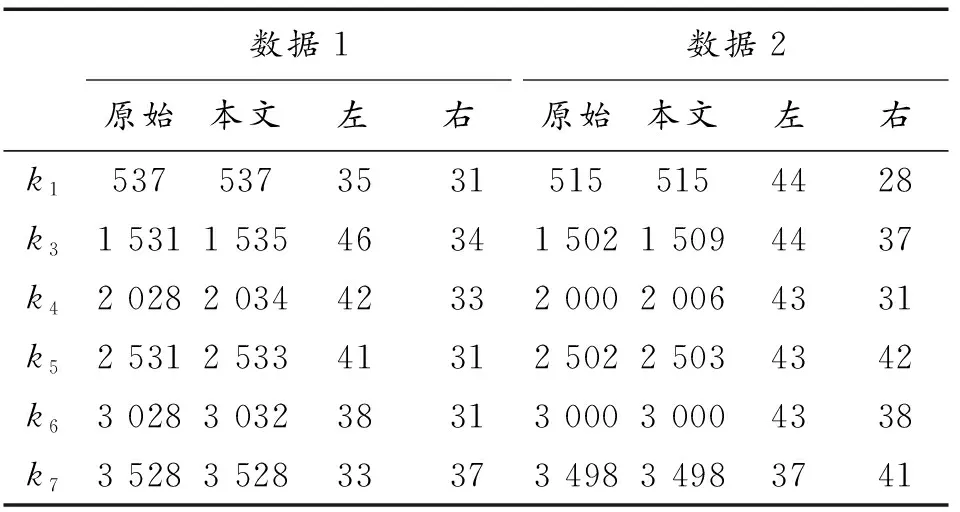
表2 条带光谱混叠范围Table 2 Spectral mixing range of strips

表2中,数据1、2的第一列代表直接计算得到的条带灰度极值点,第二列代表本文方法所计算的灰度极值点,第三、四列分别代表灰度极值点左右两侧的光谱混叠范围。从表2中可知,两组数据灰度极值点存在将近20个像素的偏差,直接计算得到的条带灰度极值并不是等间隔分布,无法保证裁剪后条带图像等宽。

另外,数据1和数据2左右两侧光谱混叠范围的最大值分别为46、37和44、42,求取平均值后条带图像左右混叠宽度为45、40,作为8谱段滤光片阵列多光谱图像光谱混叠范围。然后,依次计算图像中各条带有效区域顶点坐标,通过构建条带图像模板得到条带有效区域图像,其灰度变化曲线如图12所示。

图12 条带有效区域灰度Fig.12 Grayscale of the effective area of the strip

其中,图12(a)、图12(b)分别对应数据1、数据2。从图12可知,利用本文方法得到的条带宽度一致,且条带有效区域不存在光谱混叠区域,而且最大程度保留了条带图像边缘重叠区域像素。

为了说明本文算法的可行性,对数据1、数据2分别采用表2中对应的条带灰度极值点确定条带有效区域,并与本文结果进行对比,条带有效区域范围如表3所示。其中,对比1、对比2利用直接计算得到的条带灰度极值点,光谱混叠宽度分别为45、40和50、50。

表3 各条带有效区域宽度Table 3 Width of the effective area of each strip

由表3可知,数据1和数据2中对比2方法采用固定的光谱混叠宽度得到的各条带有效区域宽度最窄,较本文算法条带有效区域宽度约窄15像素左右;而对比1方法中采用的光谱宽度与本文算法一致,虽然计算的各条带有效区域宽度与本文算法较为相近,但得到的波段2至波段7条带有效区域宽度并不相同。

为了进一步说明本文算法的有效性,以数据2中第4波段条带图像为例,利用上述方法计算的条带有效区域范围分别计算条带图像行像素灰度变化曲线,如图13所示。

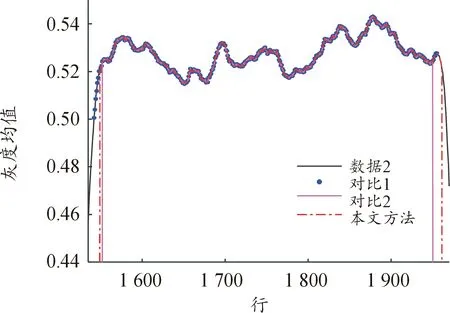
图13 条带有效区域对比Fig.13 Comparison of effective areas of strips

由图13和表3可知,虽然对比1计算得到的条带有效区域宽度与本文算法相近,但条带边缘处仍存在部分光谱混叠,如图13中箭头所指的区域;对比2在去除光谱混叠区域同时将部分有效区域也裁剪掉,如图13中虚线圆圈处,故条带有效区域范围最少。而本文算法得到的条带有效区域在条带中间区域,行像素灰度均在主要集中在0.52附近,且行方向的重叠区域像素较2种对比方法多。

由此可知,本文中基于图像行像素灰度均值确定条带图像有效区域,不仅去除了条带中光谱混叠区域,且最大程度上保留了条带图像边缘像素,有效解决了滤光片阵列多光谱图像条带有效区域无法精准确定问题

4 结论

针对航空滤光片阵列多光谱图像条带裁剪范围确定问题,提出基于行像素灰度的多光谱图像条带预处理算法,通过图像行像素灰度均值计算条带灰度极值点与最大光谱混叠范围,用于确定条带图像有效区域的四个顶点坐标。通过实验对比,表明条带预处理算法能够最大限度保留边缘区域像素、提高条带重叠率,且有效区域像素灰度不存在光谱混叠,可以满足条带图像的后期处理及应用需求。