基于凸包计算和小波变换的显著目标检测算法

谭永前,曾凡菊,2

(1.凯里学院 大数据工程学院, 贵州 凯里 556011;2.重庆大学 光电工程学院, 重庆 400044)

0 引言

Itti等[1]在1998年首次提出视觉注意力机制的概念,这种视觉注意力机制受人类认知生理和心理的控制,是人类处理各种视觉信息的一种重要机制。受人类这种处理视觉信息注意力机制的启发,众多学者开始把计算机模型与视觉注意力机制相结合,开启了计算机视觉领域对于图像显著性检测的研究[2-4]。一幅图像的显著性可定义为图像中的主要组成元素吸引人类视觉注意的能力,其显著性检测可定义为采用计算模型检测图像中最吸引人类视觉注意力、最令人感兴趣、视觉表现力最强的区域[5-6]。由于图像的显著性检测是模仿人类视觉注意力机制过程,因此可通过一系列的算法处理来获取图像中最能吸引人类注意力的区域或目标,能够大大降低图像后续处理的复杂度和节省存储空间。因此,图像的显著性检测被广泛应用于计算机视觉领域,如目标检测[7]、目标跟踪[8]、视觉跟踪[9]、语义分割[10]等。

目标检测是为了突出显著区域,显著目标检测经过多年的不断发展,可分为两大类:一类算法是基于低层特征不需要经过学习的自下而上的方法;另一类算法是基于高层特征信息需要通过不断学习的自上而下的方法。

基于低层特征不需要经过学习的自下而上的方法[11-14],该类方法直接利用相关先验信息,通过底层的像素等信息进行计算,需要人工提取特征,达到将显著目标区域与其背景进行区分的目的。Yan等[12]采用图像的全局颜色对比度与中心先验相乘作为单尺度下的显著性度量值,该方法得到的显著图存在背景干扰的问题,在对背景复杂的图像进行显著性检测时效果欠佳;Tong等[13]使用图像的中心先验与局部颜色对比度相乘的方法来计算显著性值,最后采用多尺度加权融合的方式得到像素级别的显著图,对边界模糊不清的情况起到一定的改善作用,但显著目标亮度不够的问题仍待解决;Zhu等[14]采用Harris角点凸包的方法实现了前景物体的近似定位,利用凸包先验图和中心偏置值相结合得到初始显著图,最后对其优化得到最终结果。Zeng等[15]提出一种线性融合的目标建议方法,并将其应用于弱监督目标检测中。崔等[16]把图像的对比度特征、颜色特征等显著性线索通过元胞自动机融合得到显著图,这种采用多线索融合方式有助于检测出图像边缘完整的显著性目标,在复杂场景图像上的检测性能得到一定提高。唐立婷等[17]提出凸包改进流行排序的显著性区域检测方法,该方法解决了传统流行排序相关显著性检测算法在处理图像时把目标影子误检,以及检测结果中显著区域被识别成背景等问题,该改进算法提高了显著目标检测的准确性。

基于高层特征信息需要通过不断学习的自上而下的方法[18-20],该类方法利用深度学习自动学习得到多尺度特征(颜色、形状、纹理等)对输入图像进行检测,达到定位图像显著性区域的目的。Hou等[18]提出跳跃结构的短链接检测算法,使得每一层具有更加丰富的多尺度特征映射,让显著性目标的边界更加清晰;Feng等[19]提出一种注意力反馈网络边界感知显著目标检测算法,该算法利用边界增强损失来获得更精确的边界,从而实现显著性目标的分割;Zhang等[20]提出利用字幕网络作为辅助网络来提高显著性目标的检测性能。自上而下显著目标检测算法[18-20]相对于传统算法在目标检测的准确性、时效性、分辨率以及利用单一网络同时完成显著性目标的检测和边界定位等方面要优于传统算法。但是,基于深度学习的显著性目标检测方法也还存在一些不足,如需要依赖于已有的大量数据进行训练,且学习训练需要多个阶段,训练步骤较为繁琐、耗时,需占用大量的存储空间,算法复杂度较高等。

自下而上的显著目标检测方算法只需提取相应的底层特征来实现显著性目标的检测,不需要经过繁琐的学习训练,速度快,耗时短。本文致力于研究和改进传统自下而上的方法,在对现有该类算法进行分析总结时,发现当前相关算法存在如下不足:① 算法在消除背景干扰时不理想,导致从复杂的背景图像中检测显著区域时效果不佳,检测准确性有待提高;② 生成的显著性目标全分辨率较低,模糊不清,且不能完整均匀高亮显著目标;③ 检测显著目标不够准确,显著目标的边界不够清晰。本文提出一种基于凸包计算和小波变换的显著目标检测算法(CHWT),首先在不同颜色空间进行凸包计算并计算凸包交集,提高了显著性检测的准确性;然后利用MR算法计算多尺度超像素分割下的显著图,融合多个尺度显著图并与凸包交集二值化掩膜进行贝叶斯融合,高亮了显著目标;最后利用小波变换对幅度谱进行多尺度小波分解,逐层消除背景干扰信息,选取较优的显著图生成多尺度小波变换显著图,并与高亮的多尺度超像素凸包显著图进行融合获得最终显著图。

1 本文算法

显著性检测的最终目的是快速、准确地把显著目标检测并突显出来,本文提出了CHWT算法模型,该模型由凸包交集模块、多尺度超像素分割融合模块以及多尺度小波变换模块组成。首先通过凸包交集模块在多个颜色空间进行凸包计算后求取凸包交集,并对凸包交集进行二值化掩膜;然后在多尺度超像素分割融合模块对图像进行多尺度超像素分割,结合MR(manifold ranking)算法[21]计算得到多尺度超像素分割显著图,利用贝叶斯模型融合凸包交集二值化掩膜,得到多尺度超像素融合凸包显著图;最后在多尺度小波变换模块对图像进行离散余弦变换(discrete cosine transform,DCT)提取幅度矩阵和符号矩阵,利用小波变换对幅度谱进行多尺度分解,逐层消除图像背景干扰,通过离散余弦逆变换(inverse discrete cosine transform,IDCT)得到多尺度小波变换显著图,对多尺度小波变换显著图和多尺度超像素凸包显著图进行优化融合得到最终显著图,本文方法流程如图1所示。

图1 本文算法流程图Fig.1 Flowchart of the algorithm in this paper

1.1 凸包计算

为了更准确地检测目标区域,减少凸包内的背景噪声,提高显著目标检测的准确性,本文采取在RGB空间、Lab空间、HSV空间分别进行特征点检测、计算凸包,然后求取3个颜色空间凸包交集作为优选凸包,并对凸包交集进行二值化掩膜的方式来凸出显著目标。本文中计算凸包方法与文献[22]中计算凸包方法存在以下不同:文献[22]中利用颜色增强Harris算子对原图像增强后仅在单颜色空间进行特征点检测并计算凸包。文献[22]方法忽略了图像在不同颜色空间中颜色取值范围会有所不同的情况,仅在单一颜色空间计算凸包,无法消除背景噪声,这会导致图像的背景噪声被包含进入凸包,影响目标检测的准确性。

本文中使用增强Harris算子[23]对原图像进行颜色增强并进行特征角点的确定,角点多边形的面积越小,表明确定的目标区域越精确。同时,为了提高算法的计算效率,采用SLIC(simple linear iteration clustering)[24]算法对图像进行超像素预分割,超像素数目N设置为200,凸包计算过程如下:

1) 对原图像进行去噪处理,消除噪声对后续确定特征角点的影响。

2) 使用Harris算子先对原图像进行颜色增强并确定特征角点。

3) 将图像边界附近区域的特征角点去除,连接剩余特征角点的最外围角点形成凸包。

将凸包的质心作为凸包中心,使用超像素分割后,中心先验显著值Sc(i)可定义为:

(1)

式中:x0、y0表示图像中心值的坐标;xi、yi表示凸包内超像素i的中心值坐标;∂w=w/3、∂h=h/3,w、h分别表示宽和高。最后将显著值Sc(i)归一化到[0,1],超像素分割结果、凸包及中心先验结果如图2所示。

图2 超像素分割、凸包、中心先验结果Fig.2 Superpixel segmentation,convex hull and center prior results

1.2 频域多尺度小波变换

本文采用小波变换对各个特征通道的幅度矩阵分别进行分解[25-26],对幅度矩阵中低频部分幅值在一定程度上进行压缩。在j尺度空间下低频子带的Mallat分解公式为:

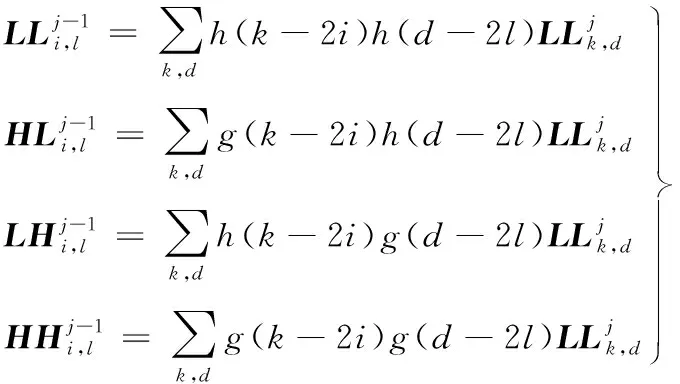
(2)

则式(2)对应的重构公式为:

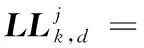
(3)

式(2)、式(3)中:h、g分别表示低通、高通;j、j-1表示进行小波分解的尺度空间;LL表示低通分量子带;HL表示水平子带;LH表示垂直子带;HH表示对角子带。

定义1图像f(x,y)的特征通道I、R、G、B的计算公式[1]为:

(4)

式(4)中,r、g、b分别表示图像f(x,y)的3个颜色通道。

定义2假设图像f(x,y)的像素为256×256,则图像的I特征通道权重因子可用式(5)计算。

(5)

其他R、G、B特征通道权重因子可用式(5)依次求得。

定义3输入原图像为f(x,y),图像分辨率为m×n,则图像f(x,y)的二维DCT频域变换F(X,Y)可定义为:

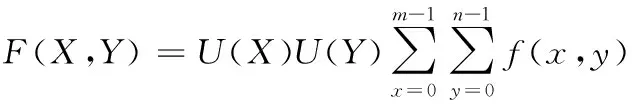
(6)

式(6)中:

定义4图像f(x,y)二维离散余弦逆变换(IDCT)可定义为:

(7)

定义5频域F(X,Y)的I通道幅度矩阵AI和符号矩阵SI提取公式定义为:

(8)

其他R、G、B特征通道的幅度矩阵和符号矩阵可用式(8)对应求得。

小波变换能够更好地分离图像的细节,在图像分解和重构中得到广泛应用,本文采用小波变换对各个特征通道的幅度矩阵进行多尺度分解和重构,达到逐层消除图像背景干扰信息的效果。本文采用式(2)、式(3)分别对特征通道的幅度矩阵进行分解和重构,重构的多尺度幅度矩阵为A′。

定义6特征通道I的多尺度特征通道MFCI可定义为:

(9)

其他R、G、B特征通道对应的多尺度特征通道可按照式(9)依次得到,则多尺度下的显著图可定义为:

Sj=G*(ωIMFCI+ωRMFCR+

ωGMFCG+ωBMFCB)

(10)

式(10)中,G为二维高斯低通滤波器。

为了从式(10)得到的多尺度显著图中选取出最优的多尺度小波变换显著图,本文采用了文献[25-27]的方法,先构建一个评价函数H对所有多尺度显著图Sj进行评测,并在评价函数中加入信息熵。信息熵在图像处理中常被用作评价图像质量的一个量化标准,本文在对多尺度的显著图进行评价时,利用图像的信息熵可以判断显著图是否优越。如果多尺度显著图的信息熵越大,表示该显著图越混乱,背景干扰越多;熵值越小,显著图的背景干扰就越小。可见评价函数H值越小,对应的多尺度显著图就越优越。评价函数H和背景干扰矩阵K定义为:

(11)

(12)

式(11)、式(12)中:E为多尺度显著图的信息熵;Sj(x,y)为多尺度显著图;K(x,y)为多尺度显著图的背景干扰矩阵;m,n分别行、列数。

为了尽可能地评测出多尺度显著图集合Sj中的优越显著图,本文借鉴了文献[28]中的思想,选取评价函数H值最小的4幅多尺度显著图按照式(13)进行最终融合,并对融合的显著图进行中央偏见优化得到最终多尺度小波变换显著图Sfinal,其计算表达式为:

(13)

式(13)中:ψ表示中央偏见矩阵;S1、S2、S3、S4表示评价函数H值从小到大的多尺度显著图集合Sj中对应的显著图;H1、H2、H3、H4分别表示其对应的评价函数值。多尺度小波变换显著图如图3所示。

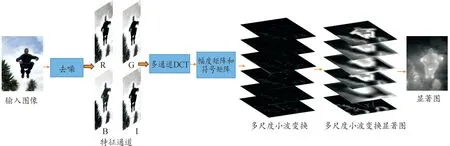
图3 多尺度小波变换显著图Fig.3 Multi-scale wavelet transform saliency map

1.3 多尺度超像素分割融合显著图

为提高算法运行效率,本文采用SLIC(simple linear iterative clustering)算法对图像进行分割预处理[24],以超像素代替像素作为处理单位。SLIC通过利用像素的颜色相似度和空间距离关系进行简单迭代聚类来实现超像素分割[24,28],该算法有存储空间效率高,呈现的边缘贴合度分割效果好,生成的超像素块紧凑均匀等特点。本文采取对原图像进行4种不同尺度的超像素分割策略,与采取单一尺度进行超像素分割不同[21-22,30-33],本文中采取的多尺度超像素分割,避免了单一尺度超像素分割时超像素数目设置不当,导致显著目标图像边缘信息丢失,破坏显著目标完整性的情况。本文中采取多尺度分割能更有效保留显著目标图像的边界信息和显著目标的完整性,更有利于获得准确的显著目标。

利用MR算法[21]求得4种超像素分割尺度对应的显著图;最后通过融合4种尺度下的显著图获得多尺度超像素分割融合显著图,如图4所示。

图4 多尺度超像素分割显著图Fig.4 Multi-scale superpixel segmentation saliency map

1.4 本文方法流程

本文方法实现步骤如下:

步骤1输入原图像,并进行去噪处理,减少噪声对后续各步骤的影响。

步骤2在RGB、Lab、HSV空间分别进行凸包计算并求取凸包交集,得到凸包交集的二值化掩膜。

步骤3对图像进行多尺度超像素分割。

步骤4利用MR算法分别求取步骤3中多种尺度下的超像素分割显著图,并对多尺度显著图进行融合。

步骤5分别对步骤2和步骤4求取似然概率和先验概率,利用贝叶斯模型进行融合得到多尺度超像素凸包显著图。

步骤6利用式(4)、式(5)计算各个特征通道以及各特征通道权重因子。

步骤7对各特征通道分别进行DCT,并利用式(6)、式(8)提取各通道的幅度矩阵和符号矩阵。

步骤8利用式(2)、式(3)对各特征通道的幅度矩阵进行多尺度小波变换,并获得各多尺度重构幅度矩阵A′。

步骤9将多尺度重构幅度矩阵A′分别与式(8)中的符号矩阵S结合,利用式(7)、式(9)进行IDCT。

步骤10利用式(10)将同种尺度的各特征通道以权重因子为系数构建该尺度下的显著图。

步骤11利用评价函数式(11)计算步骤10中的显著图评价函数数值。

步骤12选取评价函数H值最小的4幅多尺度显著图按照式(13)进行最终融合,并对融合的显著图进行中央偏见优化得到最终多尺度小波变换显著图Sfinal。

步骤13对步骤5和步骤12进行线性融合并进行优化得到最终优化显著图。

2 实验结果及分析

2.1 实验环境和数据集

为了验证和评测本文所提方法模型的有效性,所有实验均在处理器为Intel(R) Core(TM) i5-8500,主频为3.00 GHz,Windows10系统环境下的Matlab2018b编程工具上进行。本文所提算法与6种传统主流算法MR[21],HC[29],WTHD[30],SF[31],RCRR[32],BFS[33]在公开数据MSRA-10k、ECSSD、HKU-IS上进行了实验对比。MSRA-10k数据集包含有10 000张自然景物、人物、动物图片,且很多图片的背景较复杂,该数据集还对图像进行了像素级别的真值标注以供测试。ECSSD数据集包含1 000幅多目标且背景复杂的图像,是目前主流对比数据集之一。HKU-IS数据集包含4 447张原图及对应的人工标注真值图,该数据集里的图片有多个分散的显著物体、显著物体与背景表观相似。每张图都按像素级别注释,常用于显著性物体检测研究。本文从定性分析、定量分析以及运行速度方面与当前6种主流算法进行了比较,对比实验中相关数据和图片来自于相关算法的开源代码运行后的实验结果,代码没有开源的,来自于相关论文。

2.2 定性分析对比

图5是本文所提算法与6种主流算法检测的显著图对比,从图5中可看出,HC算法能检测到显著区域,且显著目标有一定的亮度,但存在较多的背景干扰,该算法没能有效消除背景信息,显著目标亮度不高;BFS、WTHD算法没能有效消除背景干扰,BFS算法背景噪声不能够被充分消除,导致检测结果中出现边界模糊现象,虽然WTHD算法采用低分辨率处理频域方法模糊了背景干扰,但显著目标仍然不够清晰,不够高亮;MR算法将前景目标作为背景区域进行计算,造成显著目标检测区域不完整,在背景复杂图片中,没能更好地抑制背景干扰,导致显著目标边界不够清晰;RCRR算法显著目标不够高亮,边界不清晰;SF算法能够提取显著目标,能高亮部分显著目标的边缘,但不能较完整地均匀显示整个显著目标,显著图也不够平滑。本文所提CHWT算法采取在不同颜色空间进行凸包计算,求取凸包交集的方法准确提取显著目标区域;利用贝叶斯模型对多个尺度显著图和凸包交集二值化掩膜进行融合,高亮了显著目标区域;利用小波变换对幅度谱进行多尺度小波分解,逐层消除背景干扰信息;本文所提算法能够有效凸显显著目标区域,消除背景干扰,能够高亮显著目标区域,显著目标区域相对其他算法更加平滑,边界更加清晰,分辨率也更高,更接近达到人工标注图的效果,如图5(i)为人工标注的真值图。

图5 本文算法与其他6种显著性检测算法的显著图对比Fig.5 Comparison of the saliency maps between the proposed algorithm and 6 other saliency detection algorithms

2.3 定量分析对比

本文采用准确率-召回率(precision recall,PR)曲线[34]、算法综合指标(F-M)、平均绝对误差(mean absolute error,MAE)、结构测量(structure measure)4个定量指标在MSRA-10k、ECSSD、HKU-IS公开数据集上对本文算法模型进行测评,并与上述6种典型算法进行对比。

2.3.1准确率-召回率曲线

以准确率为纵坐标,召回率为横坐标,构成P-R曲线,计算公式为:

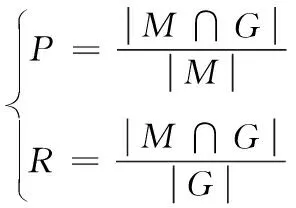
(14)

式(14)中:M是二值化的显著图像;G是与M与之对应的人工标注真值图像;|·|表示M与G的映射中像素的数目。本文算法与6种显著性检测算法在上述3个数据集上的P-R曲线对比如图6所示。

图6 显著性检测算法在3个数据集上的准确率-召回率曲线比较Fig.6 Comparison of precision-recall curves of saliency detection algorithms on three datasets

图6(a)是本文算法与6种现有算法在MSRA-10k上的PR曲线对比结果,通过对比分析可以看出,本文所提方法在召回率相同的情况下准确率略高于WTHD、RCRR、BFS算法;与MR、SF、HC算法相比,本文所提算法优势较明显,说明本文所提算法准确性能更好,较高的准确率说明检测出的目标区域更接近于人工标注的真值图。随着召回率的增加(0.85-1),分割阈值逐渐减小,数据集上图片中更多区域被判断为显著区域,所以各个算法对应的准确率逐渐下降。

图6(b)是本文算法与6种现有算法在ECSSD的PR曲线对比结果,与在MSRA-10k上的结果相比,各个算法在ECSSD上的准确率都有所下降,这是因为ECSSD数据集中的图片前景和背景相对MSRA-10k数据集更复杂,各算法检测精度有所下降。从图6(b)对比结果可以看出,本文所提算法在对更为复杂的图片进行显著性检测时,准确率与WTHD算法较接近,性能优于其他算法。本文所提算法在面对背景和前景更为复杂的图片时,与其他算法相比,仍能保持一定的检测准确率优势,说明本文所提算法有较好的鲁棒性。

图6(c)是本文算法与6种算法在HKU-IS数据集上的对比结果,从PR曲线对比结果可以看出,MR、SF、HC算法的准确率、召回率比较接近;本文算法优于其他算法。

2.3.2算法综合指标

算法综合指标常用来对算法模型进行整体性能的评价,计算公式为:

(15)

式(15)中:β2设置为0.3[31],用于调节P和R权重;Fβ值越大表明算法模型整体性能越好。

2.3.3平均绝对误差

平均绝对误差的差值越小,表明显著图与真值图就越相似,计算公式为:

(16)

式(16)中:W、H分别表示图像的宽和高;S(x,y)表示(x,y)在显著图上的像素值;G(x,y)表示(x,y)在人工标注真值图上的像素值。

2.3.4结构测量

SM[35]用于度量评估显著图和真实显著图之间面向区域和物体的结构相似性,计算公式为:

SM=α×SW+(1-α)×SQ

(17)

式(17)中:α取值0.5;SW为面向物体的结构性相似度量;SQ为面向区域的结构性相似度量。SM值越大表明显著图与人工标注真值图越相似。

本文所提CHWT算法与上述6种算法在3个数据集上的Fβ、MAE、SM指标对比,如表1所示。

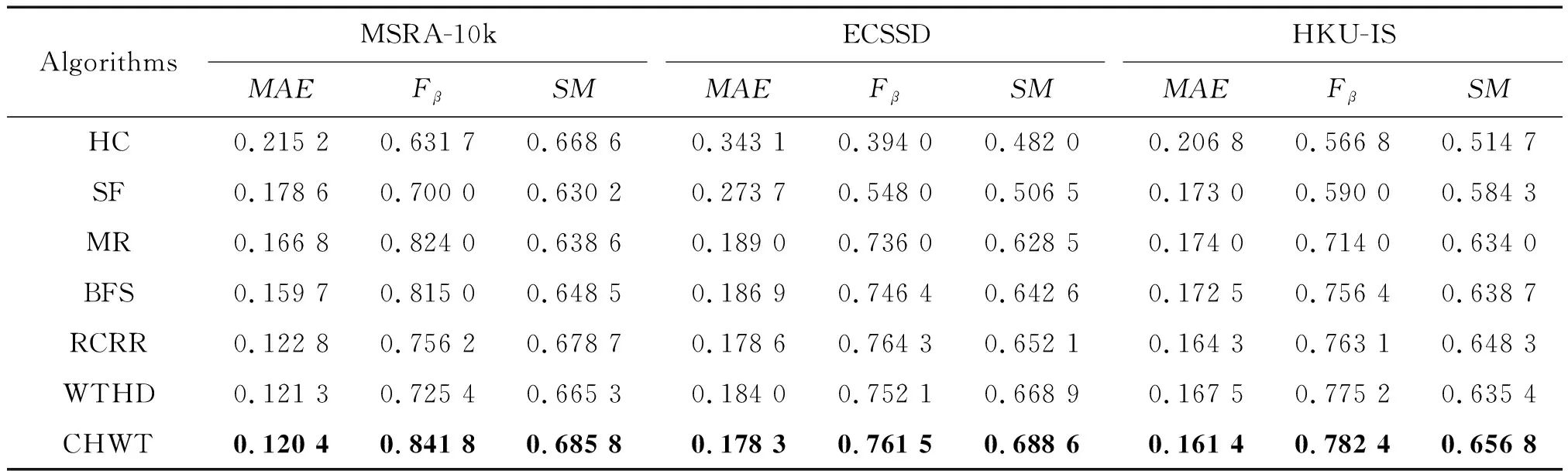
表1 MAE、Fβ、SM在3个数据集上的定量结果对比

表1统计了本文所提算法与6种算法在MSRA-10k、ECSSD、HKU-IS上的定量指标,表中的数据数值代表了该数据集上相应评估指标参数的平均值。根据表1中的数据对比结果,CHWT算法在MSRA-10k数据集上3种定量指标表现均优于其他算法;在ECSSD数据集上,本文所提算法在MAE、SM指标上优于其他算法,在Fβ指标上略低于RCRR算法,优于其他算法;在HKU-IS数据集上,本文所提算法在MAE、Fβ、SM指标上均优于其他算法。

通过对数据集中的图像进行分析,结合表1中的定量对比结果,发现MSRA-10k、ECSSD数据集中的显著性目标的区域面积较大,MSRA-10k数据集上的图片背景较其他2个数据集要单一;HKU-IS数据集上有多个分散的显著区域,背景较复杂。结合本文所提算法在以上数据集上的表现,可以推断本文所提算法在检测背景较单一,显著目标区域面积较大时表现良好;在检测有分散目标区域,背景较复杂时表现还不够稳定。

2.4 计算速度对比

算法计算速度是评测算法模型的一项重要指标,在保障一定准确率的前提下,更快的计算速度表明该算法拥有更优秀的整体性能,更低的算法复杂度,更容易被用于实时系统。表2对本文算法和6种算法在3个数据集上的算法运行平均时间进行了统计,本文算法与SF、MR、BFS、RCRR、WTHD算法都使用了超像素分割算法。HC算法是基于直方图对照度的方法,每个像素的显著性值是由它与图像中全部其他像素的颜色差异来确定的,该方法虽然速度较快,但在复杂场景中难以有效去除背景信息的干扰,不能有效整体突出显著目标;WTHD算法是在频率域中计算显著性,在频率域进行显著性计算,算法复杂度低、运行时间快,所以该算法效率最高,但显著目标的准确率和分辨率较低,仅能突出目标的边界区域,不能高亮显著目标;RCRR算法虽然也采用了分割算法,但由于算法在计算显著性回归校正过程和正则化随机游走排名模型时消耗了一定时间,在一定程度上影响了算法运行的效率。可以看出,本文算法与同样使用分割算法的SF、MR、BFS算法基本处于同一数量内,但本文算法对显著目标区域的检测精度更高,不仅能完整地高亮显著目标,还有效抑制了背景噪声的干扰,获得了更高质量的显著目标检测图。本文所提算法以较小的时间代价取得了比其他算法更高的显著目标检测精度,并完整高亮了显著目标,获得更高质量的显著图,表现出了更好的鲁棒性。

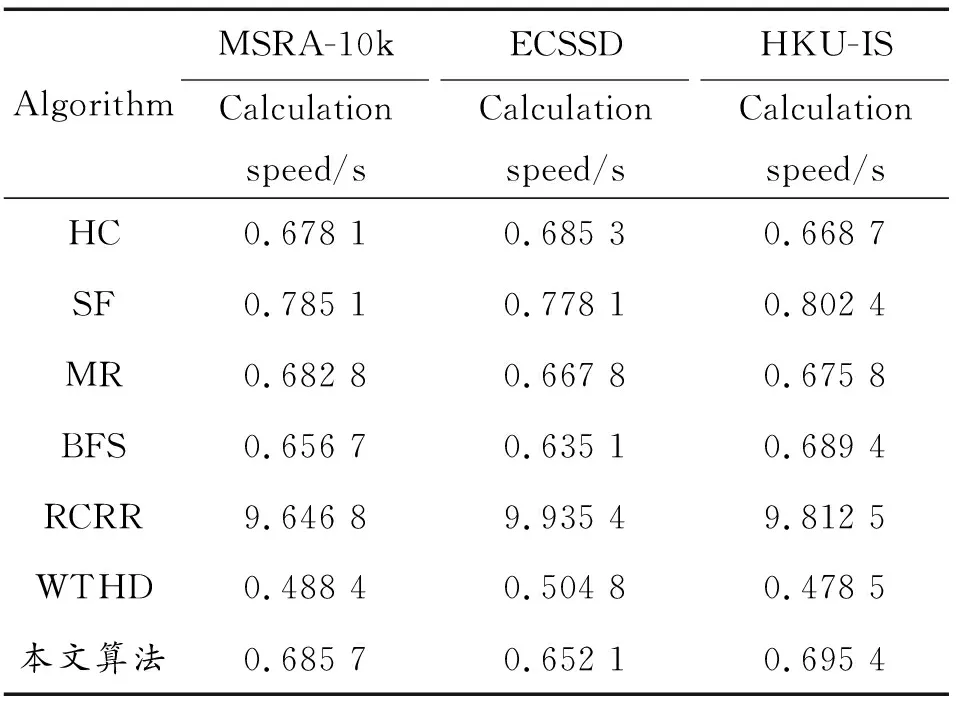
表2 算法计算速度对比

3 结论

本文所提基于凸包计算和小波变换的显著性检测算法(CHWT),通过选取不同颜色空间下的凸包交集作为合理凸包,有效提高了显著性检测的准确性。利用贝叶斯模型融合多尺度超像素凸包显著图,达到高亮显著区域的目的。利用小波变换对幅度谱进行多尺度分解,逐层消除背景干扰,最终达到消除背景噪声的效果。在公开数据集MSRA-10k、ECSSD和HKU-IS进行了测评,实验结果显示,本文所提算法在准确率-召回率曲线(PR曲线)、算法综合指标(F-Measure)、平均绝对误差(MAE)和结构测量(SM)指标上优于其他算法,本文所提算法表现出更好的准确性和鲁棒性。对于图像中有多个显著性目标或者当显著性目标的边界连通性不够连续时,本文算法检测效果仍不够理想,未来将继续探索多目标检测方面的研究,以提高显著性检测的准确性。