基于改进 A*算法的大型织机车间运载机器人路径规划

龚闯　戴程浩　江维　于俊康　陈振

摘要：大型织机车间运载机器人是一种实现在织机车间内向指定位置进行物料转运工作的一种智能化装备。由于在织机车间内智能运载机器人需要结合运载需求并通过避障选择不同路径到达目标位置，因此如何对机器人的路径进行规划和优化是提升机器人运输效率的关键。针对A*算法规划路径不够平滑的问题，对规划路径进行贝塞尔曲线优化，使得路径平滑连续，提高运载机器人的运输效率。针对规划路径距离障碍物较近，存在安全风险的问题，采用障碍物膨胀优化，为运载机器人在运输过程中设置了安全区域，提高机器人在运输过程中的安全性。针对传统A*算法搜索速度慢的问题，采用多段动态加权方法改进传统A*算法的启发函数，提高算法路径规划搜索速度。最后，结合大型织机车间工作环境，搭建了仿真平台，仿真结果表明，相比传统 A*算法，采用多段动态加权改进的 A*算法在路径规划速度方面提升了39.8%，经过贝塞尔曲线与障碍物膨胀优化的多段动态加权改进A*算法其路径规划速度提升了45.2%，验证了所提出的大型织机车间运载机器人改进A*路径规划算法的可行性和有效性。

关键词：织机车间机器人；路径规划；改进A*算法；贝塞尔曲线；启发函数

中图分类号：TP391     文献标志码：A   文章编号：2097-2911-（2023）02-0057-11

Path Planning of Transport Robot in Large Loom WorkshopBased on Improved A* Algorithm

GONG Chuang1， DAI Chenghao1， JIANG Wei1， 2*， YU Junkang1 ， CHEN Zhen1， 2

（1. School of Mechanical Engineering and Automation， Wuhan Textile University Wuhan， 430200， China;

2. Hubei Provincial Key Laboratory of Digital Textile Equipment， Wuhan Textile University， Wuhan， 430200， China）

Abstract：The large- scale loom workshop transport robot is an intelligent equipment designed for material transportation within weaving workshops to specified locations. As intelligent transport robots within the weaving workshop need to combine transportation requirements and navigate through different paths to reach the target location while avoiding obstacles， how to plan and optimize the robot's path is crucial for enhancing transport efficiency. In response to the issue of the lack of smoothness in the path planned by the A* algorithm， the planned path is optimized using Bezier curves， resulting in smoother and continuous paths， thus improving the efficiency of the transport robot during transportation. In response to the issue of safety risks associated with the proximity of the transport vehicle to obstacles， obstacle expansion optimization is adopted to set up a safe area for the robot in path planning， improving its safety during transportation. In response to overcome the slowsearch speed of the traditional A* algorithm， a multi-segment dynamic weighting method is applied to improve the heuristic function of the A* algorithm， thereby enhancing its search speed. Lastly， considering the working environment of the large- scale weaving workshop， a simulation platform is constructed. Simulation results indicate that compared to the traditional A* algorithm， the multi- segment dynamic weighting improved A* algorithm enhances path planning speed by 39.8%. Furthermore， the path planning speed is improved by 45.2% through the adoption of the multi- segment dynamic weighting improved A* algorithm with Bezier curve optimization and obstacle inflation optimization. These findings validate the feasibility and effectiveness of the proposed improved A* path planning algorithm for the large- scale weaving workshop transport robot， as presented in this paper.

Key words： loom workshop robot；path planning；improved A * algorithm；Bezier curve；heuristic function

引言

纺织行业是全球制造业中的重要组成部分，随着市场需求的不断增加和技术进步的推动，纺织生产车间面临着生产更高效、更灵活、更智能的要求。纺织车间智能运输机器人是一种自主导航智能机器人，专门用于在纺织车间内执行物料运输任务，优化物料搬运过程，提高生产效率和安全性，实现纺织生产过程的智能化、自动化和绿色化生产。大型纺织车间环境复杂，机器人如何在多变车间环境中实现高效的自主导航和避障，如何规划机器人路径来提高搬运效率，这些关键技术需要结合纺织车间的特点和需求进行深入分析和研究，是推进纺织车间运载机器人实用化的重要方面。

路径规划分为全局规划和局部规划[1]，全局规划为已知环境信息基本不变化，即为相对静态的环境下的路径规划。局部规划是在未知环境中进行规划，环境信息多变，环境信息掌握不全面，大多为动态环境下的路径规划。目前已有多种算法被用作路径规划中，如遗传算法[2-4]、粒子群算法[5-7]、蚁群算法[8-9]等群体智能算法，也有进行局部规划的DWA算法[10-11]， 同时也有D*lite[12-13]， A*算法[14-17]等启发式算法[18]，这些算法在机器人路径规划中应用并取得了一些实际应用成果。当采用A*算法进行路径规划时，存在搜索速度慢，规划路径距离障碍物过近，规划路径不平滑等问题。针对A*算法中搜索范围广，节点拓展慢的问题，文献[19]提出了一种时间优先的A*算法，该算法仅在节点领域存在障碍物有障碍物碰撞风险时计算启发值，以牺牲一定的路径长度和光滑性为代价， 提升了计算效率。文献[20]提出通过构建栅格间夹角关系的交叉积公式对启发函数进行改进， 合理的缩小了算法搜索范围，提高了搜索速度。文献[21]通过改进评价函数的方式，减少了算法搜索范围，但路径的安全性有待提高。针对 A*算法规划路径不平滑，转折角过大，转折点较多的问题，文献[22]提出通过B样条曲线的方式对该问题进行优化，对于路径平滑度有了提升但是路径安全度仍然有待提高，针对A*算法规划路径距离障碍物较近的问题，文献[23]提出对障碍物矩阵进行节点拓展的方法，成功达到了避开障碍物的目的，但其搜索出的路径面临转折角过多的问题。

综上所述，针对上述问题，本文提出了一种基于改进 A*算法的大型织机车间运载机器人路径规划方法，并从三方面对传统 A*算法进行优化，首先，采用贝塞尔曲线对 A*算法规划路径进行优化，使路径平滑，优化纺织车间运载机器人运输过程。然后，采用障碍物膨胀优化，设置安全区域，使得机器人避开障碍物，提升纺织车间机器人运输安全性。最后，采用多段动态加权方法改进启发函数，提升了算法搜索速度，通过三方面的优化，从总体上提高纺织车间运载机器人运输效率和实用化水平。

1 A*算法原理与改进

1.1路径规划算法比较与选择

为了更好分析A*算法优势，从搜索方向、启发式、增量式、应用限制以及算法的适用范围四个方面进行不同路径规划算法的性能比较，结果如表1所示。

纺织车间是一个相对静态环境，并且纺织车间内的固定障碍物信息已知，由此可采用地图信息已知的静态规划算法，通过表1对比静态规划算法可知，A*算法具有明显优势，首先A*算法是通过对Dijkstra的借鉴和改进，建立了基于启发函数的搜索模型，从而对Dijkstra这种遍历搜索方法造成的搜索点过多的缺点进行了优化，另外在算法构建方面，A*算法结合了 BFS 算法优点和Dijkstra的优势，同时结合了速度优势与精度优势，能够很好完成环境信息已知的路径规划任务。

1.2传统A*算法原理

A*算法搜索原理是起点与终点之间的代价最小，建立起点与终点之间的代价函数就是A*算法的启发函数，其表达式为（1）式。

FN= GN+HN（1）其中G表示节点间的实际代价值，H表示到目标节点的代价估计值，F是节点总代价值。有两种常用距离计算启发函数，曼哈顿距离和欧氏距离，式（2）为欧氏距离的H值估计，其中p.x、p.y为当前节点的X，Y轴坐标，g.x、g.y为目标节点的 X，Y轴坐标，D为搜索域的最小单位距离。

曼哈顿距离则表现为横向和纵向的距离，式（3）为曼哈顿距离的H值估计。

HN=D*absp.x -g.x+absp.y -g.y（3）

曼哈顿距离与欧氏距离都可以满足路径规划中代价值的计算，本文选用欧氏距离作为H值的估计。图1为起点到终点的一条路径图，其路径为起点经过三个父节点到达终点，父节点2避免对子节点1进行重复搜索，因此加快了算法的搜索速度，同时在搜索过程中A*算法避免搜索重复节点。

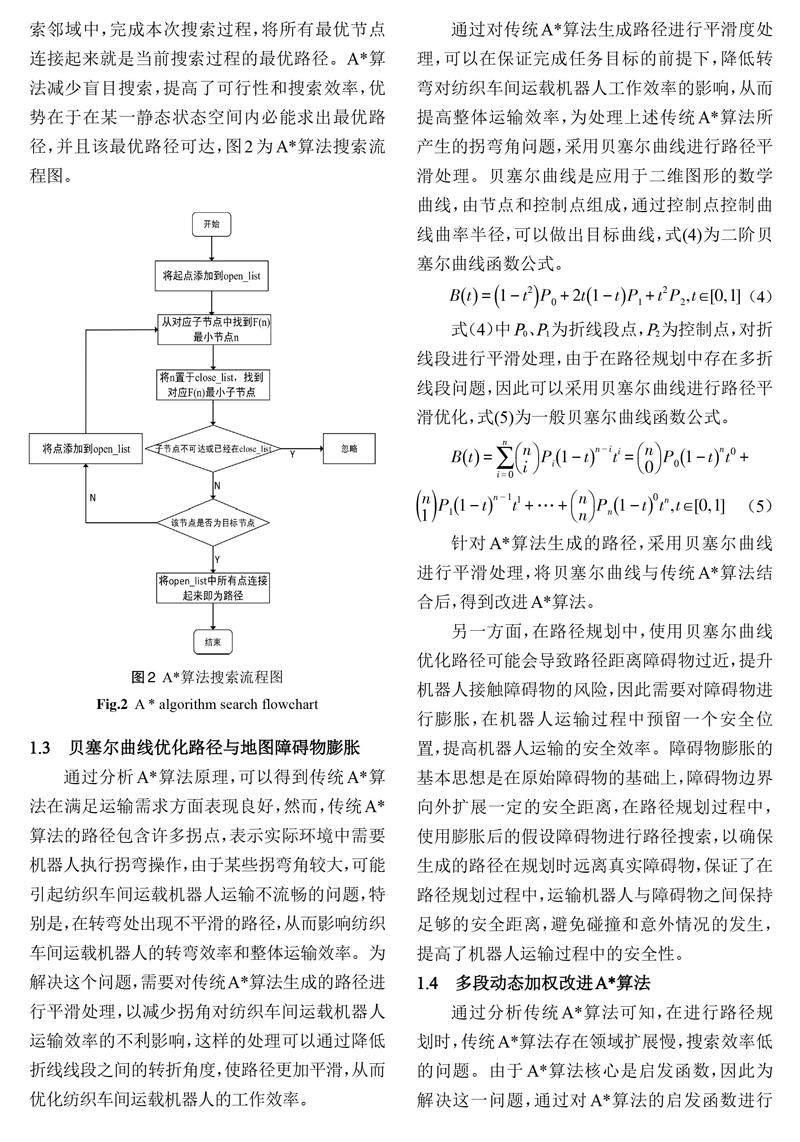
A*算法从起点开始搜索，设起点代价为0，搜索起点相邻的8个节点，根据启发函数确定最优节点，基于最优节点往外向其相邻的节点进行相同的扩展搜索，按照这种搜索过程，找到每一次搜索中的最优节点，当终点位于上一节点的搜索邻域中，完成本次搜索过程，将所有最优节点连接起来就是当前搜索过程的最优路径。A*算法减少盲目搜索，提高了可行性和搜索效率，优势在于在某一静态状态空间内必能求出最优路径，并且该最优路径可达，图2为A*算法搜索流程图。

1.3贝塞尔曲线优化路径与地图障碍物膨胀

通过分析A*算法原理，可以得到传统A*算法在满足运输需求方面表现良好，然而，传统A*算法的路径包含许多拐点，表示实际环境中需要机器人执行拐弯操作，由于某些拐弯角较大，可能引起纺织车间运载机器人运输不流畅的问题，特别是，在转弯处出现不平滑的路径，从而影响纺织车间运载机器人的转弯效率和整体运输效率。为解决这个问题，需要对传统A*算法生成的路径进行平滑处理，以减少拐角对纺织车间运载机器人运输效率的不利影响，这样的处理可以通过降低折线线段之间的转折角度，使路径更加平滑，从而优化纺织车间运载机器人的工作效率。

通过对传统A*算法生成路径进行平滑度处理，可以在保证完成任务目标的前提下，降低转弯对纺织车间运载机器人工作效率的影响，从而提高整体运输效率，为处理上述传统A*算法所产生的拐弯角问题，采用贝塞尔曲线进行路径平滑处理。贝塞尔曲线是应用于二维图形的数学曲线，由节点和控制点组成，通过控制点控制曲线曲率半径，可以做出目标曲线，式（4）为二阶贝塞尔曲线函数公式。

式（4）中P0、P1为折线段点，P2为控制点，对折线段进行平滑处理，由于在路径规划中存在多折线段问题，因此可以采用贝塞尔曲线进行路径平滑优化，式（5）为一般贝塞尔曲线函数公式。

针对A*算法生成的路径，采用贝塞尔曲线进行平滑处理，将贝塞尔曲线与传统A*算法结合后，得到改进A*算法。

另一方面，在路径规划中，使用贝塞尔曲线优化路径可能会导致路径距离障碍物过近，提升机器人接触障碍物的风险，因此需要对障碍物进行膨胀，在机器人运输过程中预留一个安全位置，提高机器人运输的安全效率。障碍物膨胀的基本思想是在原始障碍物的基础上，障碍物边界向外扩展一定的安全距离，在路径规划过程中，使用膨胀后的假设障碍物进行路径搜索，以确保生成的路径在规划时远离真实障碍物，保证了在路径规划过程中，运输机器人与障碍物之间保持足够的安全距离，避免碰撞和意外情况的发生，提高了机器人运输过程中的安全性。

1.4多段动态加权改进A*算法

通过分析传统A*算法可知，在进行路径规划时，传统A*算法存在领域扩展慢，搜索效率低的问题。由于A*算法核心是启发函数，因此为解决这一问题，通过对A*算法的启发函数进行改进来提高算法搜索速度，提升纺织车间运载机器人的运输效率。由式（2）可知，G（N）是固定值，由此改进启发函数是通过 H（N）进行的，采用设置权重方法改进启发函数，调整G（N）和 H（N）对启发函数的影响，权重分配有固定权重与动态权重两种，在搜索过程中，采用全局固定权重的方法，表示在路径搜索中只倾向考虑路径预估代价或者路径实际代价，这样设置权重会导致算法适应性差，因此为了综合改进算法，采用动态加权方法动态地调整G（N）和 H（N）的影响，通过设置不同的权重平衡预估代价与实际代价之间的关系，最后通过综合分析纺织车间的环境，以及平衡搜索速度与规划路径之间的关系，采用三段动态加权方式改进启发函数，改进后启发函数为式（6）。

式（6）中 H（N）为代价估计值，h 为不同阶段的权重判断估计值，w 为不同阶段权重值。通过对不同的搜索阶段赋予不同的权重值，采用多段动态权重赋值能够同时满足算法搜索速度和搜索路径准确性的需求。通过设置三个权重值，将搜索过程分为三个阶段，在第一阶段，倾向于搜索以预估代价为主的路径，此时算法搜索更倾向于搜索速度的提升；在第二阶段，降低预估代价对搜索路径的影响，降低搜索速度，提升搜索路径的准确度；第三阶段，再次降低预估代价对搜索路径的影响，更多地考虑实际代价。通过对传统A*算法的启发函数采用多段动态加权的方法改进，再通过贝塞尔曲线与障碍物膨胀进行优化，最终得到综合改进的A*算法，最后得到兼顾算法搜索速度与算法准确性的规划路径算法。

2纺织车间运载机器人路径规划仿真

2.1纺织车间环境与地图建模

纺织车间是专门用于纺织原材料加工和制造的场所，其结构和布局旨在支持高效的生产流程和可靠的生产质量，车间中涉及多个作业工序和设备，以及多条传送带以及物料运输用于将纤维原料转化为各种纺织产品。纺织车间作为运载机器人的工作环境，其主要特点为环境内各种传送装置与物料装置长期固定，车间内部布局稳定，在长时间内不会进行改变，因此能够表明其障碍物布局为相对静态的环境，在客观上降低了不确定性的风险。通过二维简化方法将纺织车间平面化，减少路径规划在空间上影响，图3为纺织车间二维环境示意图。

为了更好分析纺织车间运载机器人的路径规划问题，将二维纺织车间示意图进一步处理。采用栅格地图法对二维纺织车间环境示意图进行建模，得到仿真地图，其建图方法是将场景内的所有事物进行二值化处理，障碍物为1，非障碍物为0，本质上是将工作环境进行单元分割，将其用大小相等的方块表示，这样栅格大小的选取是影响规划算法性能的一个很重要因素，栅格较小时，栅格地图中的环境信息会非常清晰，但会增大信息存储量，干扰信号也会随之增加，规划速度会相应降低，实时性得不到保证；反之，栅格较大时，由于信息量少，抗干扰能力有所增强，规划速度随之增快，但环境信息会变得模糊，不利于有效路径规划，图4为模拟纺织车间环境示意图。

2.2仿真实验

为了验证本文对传统 A*算法改进的有效性，采用Pycharm作为仿真环境，在该环境内利用Python进行可视化的路径规划仿真。首先验证贝塞尔曲线对传统A*算法生成路径的优化，是否能够对路径进行平滑处理，以及通过障碍物膨胀优化后，优化路径是否远离障碍物，达到设置安全区域的效果。然后对多段动态加权改进后的A*算法进行仿真，并且与传统A*算法进行结果比较。最后将贝塞尔曲线与障碍物膨胀分别对多段动态加权改进A*算法和传统A*算法进行优化，并对仿真结果比较。

2.2.1贝塞尔曲线与障碍物膨胀优化仿真

为验证贝塞尔曲线和障碍物膨胀对于传统 A*算法规划路径的改进效果，以及优化对于传统A*算法的搜索速度的影响，同时为了验证不同任务均可进行路径优化，设置两个任务进行验证，将起点和终点坐标化，设任务一起点为（-15，0），任务一终点为（40，20），设置任务二起点为（40，20），终点为（88，95），图5为任务一贝塞尔曲线和障碍物膨胀优化结果图。

对图5（a）和图5（c）的仿真结果分析可知，经过贝塞尔曲线平滑处理后，路径平滑度提高。通过观察图5（b）和图5（d）的局部放大图，贝塞尔曲线能够平滑处理多折线段路径。分析图5（d）和图5（f）可知，经过障碍物膨胀优化后，路径远离障碍物，在规划路径中设置安全区域。为验证这一结果，对任务二进行仿真，图6为任务二仿真结果对比图。

对任务二的仿真结果进行分析，任务二仿真结果与任务一整体相同，可以得到，贝塞尔曲线优化能够对规划路径进行平滑处理，降低了折线角对于纺织车间运载机器人的影响，使得运载机器人在转弯处更加稳定和高效，同时经过障碍物膨胀优化，规划路径远离障碍物，成功设置安全区域，提高机器人执行运输任务途中的安全性，因此这两个改进为纺织车间运输系统带来了改善。

另一方面，为验证贝塞尔曲线和障碍物膨胀对于A*算法的搜索速度的影响，进行了路径搜索时间的对比验证，为降低误差，路径搜索时间取5次仿真时间平均值作为结果。验证结果见表2。

分析表2可知，贝塞尔曲线优化对于算法搜索速度并无明显影响，但经过障碍物膨胀以后，算法速度有所加快，其原因是障碍物膨胀后，算法搜索过程中有些区域被视作安全区域，避开搜索，因此提高了算法搜素速度。分析图5与图6可得，采用障碍物膨胀以及贝塞尔曲线优化路径，可以优化运载机器人运输过程，设置安全区域，可以使得运载机器人避开障碍物，提高了运载机器人的安全性和运输过程的连续性。

2.2.2多段动态加权启发函数改进仿真

为验证多段动态加权方法对于路径规划效率的影响，通过与传统A*算法进行仿真结果对比，分析搜索速度的提升，验证多段动态加权方法的可行性，设置任务三，起点为（-16，0），终点为（60，80），采用多段动态加权改进A*算法和传统 A*算法同时对任务三进行仿真，并且采用贝塞尔曲线和障碍物膨胀对改进A*算法规划路径进行优化，图7为仿真结果对比图。

分析图7（a）和图7（b）可知，动态加权改进A*算法搜索区域小于传统A*算法，分析图7（c）和图7（d）可知，贝塞尔曲线能够对改进A*算法规划路径优化，提升了改进A*算法规划路径的平滑度，分析图7（e）和图7（f）可知，障碍物膨胀优化能够与改进A*算法结合，成功设置安全区域。为了具体验证改进A*算法路径搜索速度的提升，以及贝塞尔曲线和障碍物膨胀优化后的改进A*算法搜索速度的提升。对改进A*算法与传统A*算法的搜索时间进行仿真记录，仿真结果对比如表3所示。

分析表3可知，在无优化情况下，多段动态加权改进A*算法相比较于传统A*算法，其路径规划速度提升了39.8%，多段动态加权改进A*算法路径规划速度显著提升，同时经过贝塞尔曲线与障碍物膨胀优化，多段动态加权改进A*算法相比较于传统A*算法，其路径规划速度提升了35.7%，经过贝塞尔曲线与障碍物膨胀优化的多段动态加权改进A*算法与无优化的传统A*算法相比，其路径规划速度提升了45.2%，综上所述，本文所提出的改进A*路径规划可行、有效。

3结论

（1）针对传统A*算法存在的相关缺陷，本文采用贝塞尔曲线对规划路径进行平滑处理，采用障碍物膨胀优化设置安全区域，采用多段动态加权改进启发函数，较好的提高了传统A*算法的搜索速度和搜索路径的安全可靠性。

（2）相比于无任何优化的传统A*算法，多段动态加权改进A*算法在路径规划速度方面取得了39.8%提升。经过贝塞尔曲线与障碍物膨胀优化，多段动态加权改进A*算法与传统A*算法相比，多段动态加权改进A*算法路径规划速度提升了35.7%，改进效果良好。

（3）经过贝塞尔曲线与障碍物膨胀优化的多段动态加权改进A*算法与未经过任何优化的传统A*算法相比，其路径规划速度提升了45.2%，改进效果良好。

参考文献：

[1]张旭，程传奇，郝向阳，等.一种兼顾全局与局部特性的机器人动态路径规划算法[J].测绘科学技术学报，2018，35（3）：315-320.

ZHANG Xu， CHENG Chuanqi， HAO Xiangyang， etal. A dynamic path planning algorithm for robots considering  global  and  local  characteristics[J]. Journal of Surveying and Mapping Science and Technology，2018，35（3）：315-320.

[3]李庆中，顾伟康，叶秀清.基于遗传算法的移动机器人动态避障路径规划方法[J].模式识别与人工智能， 2002， 15（2）：161-166.

LI Qingzhong， GU Weikang， YE Xiuqing. A dy- namic obstacle avoidance path planning method for mobile robots based on genetic algorithm[J]. Pattern  Recognition  and Artificial  Intelligence， 2002， 15（2）：161-166.

[4]CHEN X N， GAO P J. Path planning and control of soccer robot based on genetic algorithm[J]. Journal of Ambient Intelligence and Humanized Computing， 2020， 11（12）：6177-6186.

[5]KARAMI A H， HASANZADEH M. An adaptive genetic algorithm for robot motion planning in 2D complex environments[J]. Computational Intelli- gence and Neuroscience， 2015， 43（4）：317-329.

[6]王翼虎，王思明.基于改进粒子群算法的无人机路径规划[J].计算机工程与科学， 2020， 42（9）：

1690-1696.

WANG Yihu， WANG Siming. UAV path planning based on improved particle swarm optimization al- gorithm[J].Computer Science Engineering， 2020， 42（9）：1690-1696.

[7]WANG B F， LI S， GUO J， et al. Car-like mobile robot path planning in rough terrain using multi- objective particle swarm optimization algorithm [J]. Neurocomputing， 2018， 282（12）：42-51.

[8]ZHANG L， ZHANG Y J， LI Y F. Mobile robot path planning based on improved localized parti-cle swarm optimization[J]. IEEE Sensors Journal，2021， 21（5）：6962-6972.

[9]张松灿，普杰信，司彦娜，等.蚁群算法在移动机器人路径规划中的应用综述[J].计算机工程与应用， 2020， 56（8）：10-19.

ZHANG Songcan， PU Jiexin， SI Yanna， etal. Over- view of ant colony algorithm application in mo- bile robot path planning[J].Computer Engineering and Applications， 2020， 56（8）：10-19.

[10]何少佳，史剑清，王海坤.基于改进蚁群粒子群算法的移动机器人路径规划[J].桂林理工大学学报， 2014， 34（4）：765-770.

HE Shaojia， SHI Jianqing， WANG Haikun. Mo- bile robot path planning based on improved ant colony particle swarm optimization algorithm [J]. Journal of Guilin University of Technology，2014， 34（4）：765-770.

[11]杨恒，李越，孙寒挺，等.路径最优的移动机器人路径规划研究[J].机械设计，2022，39（08）：58-67. YANG Heng， LI Yue， SUN Hanting， etal. Re- search on path planning for mobile robots with optimal path[J]. Mechanical Design，2022，39（08）：58-67.

[12]杨桂华，卫嘉乐.基于改进A*与DWA算法的物流机器人路径规划[J].科学技术与工程，2022， 22（34）：15213-15220.

YANG Guihua， WEI Jiale. Logistics robot path planning based on improved A * and DWA algo- rithms [J]. Science Technology and Engineering， 2022，22（34）：15213-15220.

[13]戴年慧，赵江铭，王傲杰，等.基于D～* Lite算法路径规划的改进方法[J].机床与液压，2022，50（2）：167-171.

DAI Nianhui， ZHAO Jiangming， WANG Aojie， etal. An  improved method  for path planning based on D～* Lite algorithm[J]. Machine Tool and Hydraulics，2022，50（2）：167-171.

[14]YU J， LIU G， ZHAO Z，etal. Improved D*Lite al- gorithm path planning in complex environment[A].2020 Chinese Automation Congress （CAC）[C].2020.

[15]邓云峥，黄翼虎.复杂动态环境下基于A*的改进DWA算法研究[J].电子测量技术，2023，46（9）：69-76.

DENG Yunzheng， HUANG Yihu. Research on Improved DWA algorithm based on A * in com- plex dynamic environment[J]. Electronic Mea- surement， 2023， 46（9）：69-76.

[16]ZHANG H， LI M， YANG L. Safe path planning of mobile robot based on improved A* algorithm in complex terrains[J].Algorithms， 2018， 11（4）：44-49.

[17]赵春宇，姜皓，徐茂竹，等.改进A*算法在无人船路径规划中的应用[J].浙江工业大学学报， 2022，50（6）：615-620.

ZHAO Chunyu， JIANG Hao， XU Maozhu， et al. Application of improved A * algorith-m in un- manned ship path planning[J]. Journal of Zheji- ang University of Technology， 2022， 50（6）：615-620.

[18]XIONG Xiaoyong， MIN Haitao， YU Yuanbin， etal. Application improvement of A* algorithm in intelligent vehicle trajectory planning[J]. Math- ematical Bio Sciences and Engineering， 2021， 18（1）：1-21.

[19]YAN Xu， GUAN Guofei， SONG Qingwu， et al. Heuristic and random search algorithm in optimi- zation of route planning for Robot s geomagnet- ic  navigation[J]. Computer  Communications，2020， 154：12-17.

[20]AKSHAY  KUMAR  GURUJI，  HIMANSH AGARWAL， D.K. PARSEDIYA. Time- efficientA* algorithm for robot path planning[J]. Proce-dia Technology，2016，23：144-149.

[21]CHEN J， LI M， YUAN Z， et al. An improved A* algorithm for UAV path planning problems[C]//2020 IEEE 4th Information Technology， Net- working，  Electronic  and  Automation  Control Conference （ITNEC）， Chongqing， China， 2020，958-962.

[22]王中玉，曾国辉，黄勃，等.改进A*算法的机器人全局最优路径规划[J].计算机应用，2019，39（9）：2517-2522.

WANG Zhongyu， ZENG Guohui， HUANG Bo， et al. Improved A * algorithm for global optimal path planning of robots [J]. Computer Applica- tion，2019，39（9）：2517-2522.

[23]陈家宝，文家燕，谢广明.基于改进A*算法的移动机器人路径规划[J].广西科技大学学报，2022， 33（1）：78-84.

CHEN Jiabao， WEN Jiayan， XIE Guangming. Mobile robot path planning based on improved A* algorithm[J].Journal of Guangxi University of Science and Technology，2022，33（1）：78-84.

[24]周超，谷玉海，任斌.基于一种改进 A*算法的移动机器人路径规划研究[J].重庆理工大学学报（自然科学版），2021，35（5）：127-134.

ZHOU Chao， GU Yuhai， REN Bin. Research on path planning for mobile robots based on an- im- proved  A*algorithm[J].Journal  of  Chongqing University of Technology （Natural Science Edi- tion），2021，35（5）：127-134.

（责任编辑：李强）