一种概率整形接收系统的研究

赵宝?周慧影?张亮?丁洋

摘要：随着数据量的快速增长，光纤通信中的数字处理能力从100G发展到400G、800G，在引入高阶调制以及高波特率的同时，各种光纤损伤使得对光发送与接收系统的要求更高，概率整形作为一种改善性能的有效方法得到了广泛的研究。从原理层面介绍了概率整形对星座点分布概率的影响，然后介绍了光通信接收系统中概率整形对均衡、频偏估计、软信息计算模块的影响。通过仿真与实验，验证了概率整形技术在高斯信道以及光通信系统中对性能均有积极的改善效果。

关键词：概率整形； 均衡； 频偏估计； 软信息

一、前言

随着大数据的快速发展，对数据容量的需求呈爆发式增长，光纤通信中的数字处理能力从100G发展到400G以及800G，在引入高阶调制以及高波特率的同时，各种光纤损伤使得对光发送与接收系统的要求更高[1-2]。概率整形技术作为一种针对星座图的编码技术，通过改变星座点的分布获得整形增益，得到了广泛的关注。同时，概率整形技术对光通信数字处理系统接收算法也提出了新的要求与挑战。

二、概率整形原理

在AWGN信道下，最佳的数据输入分布不是平均分布，而是高斯分布。概率整形的基本原理就是改变星座点的概率分布，使得输入数据趋向于高斯分布，从而获得性能增益更接近香农极限。

概率整形普遍使用的概率分布为Maxwell-Boltzmann分布，如式（1）所示。

其中，M为不同幅度值的个数；v为整形因子，取值区间为0～1。该式针对一维符号的概率分布公式，对于QAM信号，如式（2）所示。

从信息论的角度，广义互信息（GMI）可以更直观地理解概率整形的意义。互信息是信息论中表征一个随机变量中包含关于另一个随机变量的信息量，计算公式为（3）所示。

广义互信息为互信息的推广，其中H（X）表示离散随机变量X的熵，p（x）为概率函数。v=0.1的概率分布如左矩阵，熵值H=3.7864；v=0.7的概率分布如右矩阵，熵值H=2.0702。结果显示如（4）。

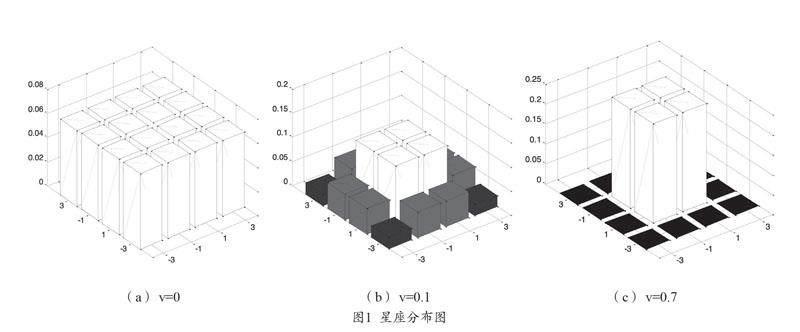
图1中（a）为平均概率分布的未整形的星座图，（b）（c）通过概率整形使得在X和Y轴上数据更趋向高斯分布。通过图1可以明显看到，随着整形因子的增加，星座的最外圈符号出现的概率不断变小，最内圈符号出现的概率不断增加，同时信息熵在减小，从4减小到2.0702。最外圈符号出现概率减小使得信号平均功率降低，换句话，在相同发射功率下星座点之间的距离变大，从而使得误码率降低，系统性能得到改善。

综上，概率整形通过增加额外的冗余，将均匀分布的输入信号改变为高斯分布或者类高斯分布，从而增大信道容量使其等于或者接近最大信道容量。

三、概率整形对接收模块的影响

二进制比特流经过或不经过概率整形，然后进行I/Q调制得到符号序列。调试符号经光纤传播到收端进行相干接收。接收端包括频偏估计和补偿、均衡、相噪估计和补偿、llr（log-likehood ratio）计算以及硬判决模块。其中，在发送数据进行概率整形情况下，频偏估计、均衡以及llr计算模块算法都需要进行一定的修正，来匹配发送调试符号概率的不均衡。本文主要分析概率整形对均衡、频偏估计、软信息计算模块算法的影响。

（一）概率整形对均衡的影响

均衡算法也可以分为基于导频的辅助方法和盲估计算法，其中盲估计算法依赖于接收信号的调制格式。当前接收器中的时域均衡采用简单恒模算法 （CMA） 以及在此基础上的修正多模算法 （MMA） ，其中恒模算法针对QPSK调制格式，多模算法针对QAM调制格式。MMA算法必须首先决定每个符号应该具有什么幅度，然后通过实际接收符号与该幅度也就是半径的误差来不断更新迭代均衡器使其达到最优。为了接近最佳运行，MMA 要求大多数决策都是正确的，这是一个很高的要求，尤其是在较低的 OSNR/高FEC开销的系统中。此外，MMA 还对高级调制格式提出了挑战，例如星座概率整形的条件下，最外圈半径的符号分布稀疏出现概率较小时会大大降低 MMA 性能。为了研究此类格式的性能，需要考虑一种不依赖于调制格式和SNR 的均衡方法。

光通信相关协议等数据帧格式中均提供了一定的pilot序列（PS），该pilot序列以一定的间隔发送。除此之外，在每个超帧头（FAW）之后还有训练序列（TS）专门用于系统链路的训练。TS和PS序列均为QPSK信号，因此可以使用CMA算法。虽然PS和TS为已知序列，但是依然采用盲均衡算法的原因是频偏依然残留在信号中，此时信号相位不可靠，CMA作为恒模算法，对信号的相位不敏感。Millar等[3]提到了一种盲均衡和非盲均衡结合的算法，也就是CMA和LMS结合的算法。该算法要求首先使用CMA算法进行粗均衡，然后使用LMS算法进行更精细的迭代更新。

概率整形时，采用PS和TS数据，使用CMA（或者结合LMS算法）可以有效改善性能，尤其是在整形因子较大外圈符号概率较小时的性能。在非PS和TS位置处的均衡系数可以使用PS和TS处的估计结果进行插值得到。

（二）概率整形对频偏估计的影响

在相干光接收系统中，频偏估计模块用来校正系统的频率偏移。频偏估计主要分为基于导频的辅助方法和盲估计算法。盲估计算法又分为BPS、4次方算法等。盲估计算法对导频没有要求，可以减少信息冗余；陈雨露[4]提出的4次方算法不需要进行大量的搜索，可以节省计算量，在没有特殊要求的系统中大多采用该算法，因此这里主要讨论4次方算法在概率整形下的性能。

Sergienko A B等[5]提到了一种加权4次方算法，应用在短序列的频偏估计中。其主要思想是放大频偏估计中的有用信号，减小无用信号也就是噪声的影响。基于Sergienko A B等[5]，Yan Q等[6]将发送符号的概率进行了引入，提出两种频偏估计算法。

方法一：

其中，yk为接收数据。R为判决门限。

方法二：

其中，rk为接收数据的幅度，φk为接收数据的相位，A4为傅里叶级数的四次谐波。

在发射数据进行概率整形的通信系统中，传统的4次方算法已经不能工作，即使增加fft的长度依然没有办法正常工作。上述两种方法可以显著地解决这个问题，得到有效的频偏估计值。但是，方法一依赖于幅值门限R的选择，随着发送数据熵值变化性能变化较大，概率整形因子很小时性能恶化严重。方法二依赖于噪声方差。噪声方差是一个统计量不是瞬态量，估计结果的准确性也会影响性能。

（三）概率整形对软信息计算的影响

对QAM采用软译码，因此需要计算log-likehood ratio，也就是似然比软值信息（LLR），Spatharakis C等[7]所示公式为：

其中， xi1、 xi0别表示第i比特为1和0的所有星座点的集合。对高斯对称信道，式（5）第二项为0。式（5）可以简化为：

对于等概率发送的数据，星座图均匀分布，式（6）中先验概率Px（x）=1/2M，可以使用Max-Log将LLR计算公式进一步简化，使用欧氏距离的计算替代式（6）中指数以及对数计算。对于经过概率整形的发送数据，显然每个发送符号的概率不同，但是幅值相同的符号发送概率相同。对16QAM存在三种发送概率，并且随着整形因子变大外圈概率变小内圈概率变大。虽然在不同的整形因子下概率在变化，但是对16QAM来说，设内圈符号发送概率为p0，外圈符号发送概率为p2，中间圈符号的发送概率为p1，则log p0/p1=log p1/p2。也就是说，相邻圈上符号发送概率的对数差是定值，基于此可以对式（6）结合Max-log算法进行简化。

四、实验和仿真

（一）AWGN信道仿真

对16QAM信号进行概率整形，在AWGN信道中传输，性能仿真如图2所示。

在图2中v表示整形因子，H表示熵值。从图2可以看到在高斯信道中，随着熵值从大变小，误码率得到改善。以ber=10-2为标准，此时，熵值从4到减小为3.25（对应整形因子从0增大到0.21），信噪比相差约3～4dB，由此可见，概率整形可以大大改善性能。

（二）光通信系统仿真

数据采用16QAM调制，分别在光背靠背场景以及经过光纤的全损伤场景下进行仿真，性能仿真如图3所示。

从图3可以看到，在不同的仿真场景下，概率整形对性能有较大的改善。当然，这个性能的改善是以更复杂的算法为代价的。除了第三小节提到的接收机符号级相关算法的修正，例如频偏估计、均衡、软信息计算等，在比特级还需要添加概率整形以及解概率整形的模块。显然，更复杂的传输系统换来了接收性能的提升。

五、结语

概率整形作为一种新的技术，它的使用不仅可以使信道容量在理论上接近香农极限，实际的光通信系统中也被证明可以大大改善接收机性能。通过搭建仿真平台，根据仿真结果可知，在成熟的接收算法基础上进行修正，可以很好地应对概率整形技术下星座概率不均衡的问题，使得概率整形技术在实际中的应用成为可能，并为高性能接收机提供一种优选方案。

参考文献

[1]余建军，迟楠，陈林.基于数字信号处理的相干光通信技术[M].人民邮电出版社，2013.

[2]王大伟.数字信号处理算法在相干光通信系统中的应用研究[D].杭州：浙江大学，2013.

[3]Millar D S ， Maher R ， Lavery D ， et al. Design of a 1 Tb/s Superchannel Coherent Receiver[J]. Journal of Lightwave Technology， 2016， 34（6）：1453-1463.

[4]陈雨露.相干光通信系统DSP补偿算法研究[D].北京：北京邮电大学，2013.

[5]Sergienko A B ， Petrov A V . Blind carrier frequency offset estimation for QAM signals based on weighted 4th power of signal samples[C]// Design & Test Symposium （EWDTS）， 2010 East-West. IEEE Computer Society， 2010.

[6]Yan Q ， Liu L ， Hong X . Blind Carrier Frequency Offset Estimation in Coherent Optical Communication Systems With Probabilistically Shaped M-QAM[J]. Journal of Lightwave Technology， 2019， 37（23）：5856-5866.

[7]Spatharakis C ， Argyris N ， Dris S ， et al. Frequency Offset Estimation and Carrier Phase Recovery for High-order QAM Constellations Using the Viterbi-Viterbi Monomial Estimator[C]// CSNDSP 2014， 9th IEEE/IET International Symposium on Communication Systems， Networks & Digital Signal Processing. IEEE， 2014.