多元线性回归模型在河流水质预测中的应用

李秋瑶

摘要：为实现基于水质自动监测数据对未来水质数据的快速预测预报，以水质自动监测数据为基础，结合统计学基本原理，基于多元线性回归模型建模，将前一日自动监测数据作为自变量，后一日各污染源因子浓度作为因变量，研究建立河流水质预测模型的变化响应关系。通过对模型的检验和校正，在试验断面上，基本达到了快速预测预警的效果，模型在实际预测中效果较好。该方法所需数据较少，预测快速，准确及时，因此，该方法可作为辅助手段应用于实际水质监测预警工作。

关键词：多元线性回归预测；河流水质预测；水质预测方法

一、前言

水质自动监测是一项与国民经济密切相关的基础工作，也是开展水质预测预警的重要前提[1]。科学准确的水质预测预警有助于认识水质变化的规律和发展态势，增加其在保障水质安全、水污染防治上的决策主动性和工作效率[2-3]。

近年来，《国务院关于印发水污染防治行动计划的通知》[4]等一系列通知，明确提出改善水环境质量的目标和要求，旨在推进重点流域污染治理，切实改善水环境质量。对于重点河流断面，持续开展水质预测，以预测数据作为后续污染防治工作决策的依据，具有重要的现实意义。

随着地表水自动监测技术的成熟和推广应用，环境监测监管部门能够实时获取监测点位的水质情况。自动监测数据监测频率高，监测时间连续，具备开展大数据统计预测的条件。各地也陆续开展了相关的研究和试点工作，利用自动监测数据开展统计预测有以下研究意义：①由于自动数据实时性高，可基于自动监测数据实现快速预测预报；②自动监测数据量大，时序性高，因此可有效提高水质预测精度；③通过基于自动监测数据的水质预测能及时感知污染风险；④通过预测值和实测值比较，当相差较大时，说明条件发生了较大变化，尤其当实测偏大时应排查异常，及时把控风险。

通常，河流水质预测采用综合指标法、平均增长率法等经验类推可以取得较好的研究结果[5]，但需要满足河流断面受周边影响小、水质变化小的前提，如河流断面水质受周边环境影响较大，其实际数据变化不规则，采用类推的方法则达不到理想的效果，因此需要采用建立模型的方法进行水质预测。目前常用定额预测法、回归分析法、灰色预测法等水质预测方法。本研究采用多元线性回归分析法进行模型建模。多元线性回归模型不仅要对回归系数进行检验，还需要对假设性和共线性作用方面进行研究与验证，从而优化变量，筛选适合的模型，增加水质预测的精确度。

二、多元线性回归方法基本原理

（一）多元线性回归模型

对于河流的水质预测，水质变化结果通常是多个因素共同影响的结果，因此，由多个自变量筛选优化后建立的多元线性回归模型，比单一自变量建立的一元线性回归模型更符合实际，更加准确与客观。目前，常规的水质自动监测因子包括：水温、pH值、溶解氧、电导率、浊度、高锰酸盐指数、氨氮、总磷、总氮等。以溶解氧为例，假定河流水质浓度与前一日各因子浓度间存在线性关系如下：

y=a₀+a₁x₁+a₂x₂+a₃x₃+…a_nx_m+ε

式中，y为因变量，x₁，x₂，x₃，……，x_m为自变量，a₁，a₂，……，a_n为回归系数；ε为随机误差，假定ε～N（μ，σ²）。

（二）数据来源

本研究根据前一日各监测因子的浓度水平来判定对当日监测因子的影响，以溶解氧因子为例，选择溶解氧作为预测因子是因为溶解氧是研究地表水自净能力的一种重要依据，相对其他因子来说，溶解氧与水温、pH及其他因子有着密切的关系，因此可以假定溶解氧浓度可通过前一日各项因子浓度进行预测。

本研究建模数据来源于2022年1月至6月广西某湖库水质自动站的监测数据日均值。该水站小时数据有效率为97.32%，日数据有效率大于99%。其有效自动监测数据的完整度和连续性为研究数据演变关系提供了很大便利，水站监测数据包括水温、pH值、溶解氧、电导率、浊度、高锰酸盐指数、氨氮、总磷、总氮。设自变量前一日水温为x₁，pH为x₂，溶解氧为x₃，电导率为x₄，浊度为x₅，高锰酸盐指数为x₆，氨氮为x₇，总磷为x₈，总氮为x₉，因变量溶解氧预测浓度为y。

三、建立方程模型

本文采用的模型基于R语言编写。首先，将训练数据输入R语言，通过线性回归模型进行建模，第一次建模得到模型拟合数据与实际数据的R²为0.9596，R²度量了多元线性回归模型的拟合优度，说明拟合优度较好，但模型反应水温、高锰酸盐指数、总磷、总氮P值较大，P值代表犯第一类错误（Ⅰ型错误）的概率，在回归方程中，体现了自变量的显著性。P值越大，说明自变量显著性越低。从第一次模型参数中得出，水温、高锰酸盐指数、总磷、总氮的显著性较低，因此将4个指标剔除后重新建模，R²为0.9594，且整体显著性与第一次建模相当，且剔除指标后由于减少了干扰，剩余指标的显著性得到了提升。可推断出因变量yi可以被前一日pH、溶解氧、电导率、浊度、氨氮浓度的线性方程进行描述，即：自变量为{x₂，x₃，x₄，x₅，x₇}。

通过重新建模，用上一日水质因子数据与当日水质因子数据，建立多元线性回归方程为：

y=4.943388-0.284600x₂+0.913373x₃-0.009313x₄+0.020536x_₅-0.602887x₇

四、模型检验

（一）模型优化

回归模型的优化主要从模型假设诊断，多重共线性进行模型的优化，首先需要诊断多元回归模型和假设相符，即模型的残差呈正态分布。其次，模型的自变量不存在多余重复信息，为简化模型提供依据。

1.模型诊断

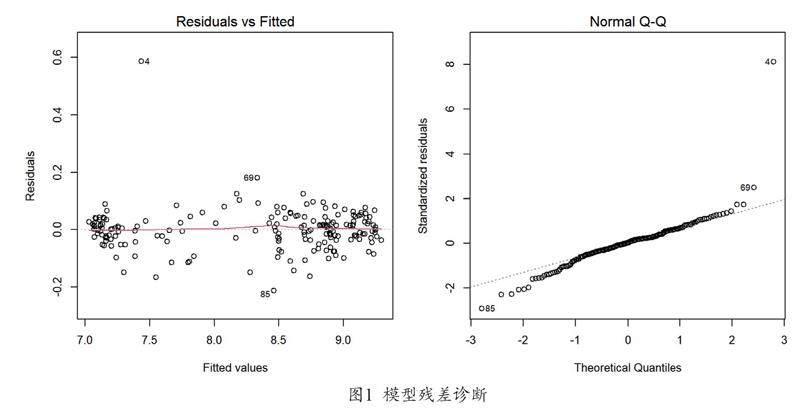
通过绘制残差图诊断模型的假定，从图1残差图中可以看出，第4点、第69点、第85点有较大残差，其中第4点的残差较大。据调查是该日藻类增加导致pH、溶解氧同时增加，pH前三日数据分别为7.16、7.14、7.23，第4日突增到8.02，溶解氧前三日数据分别为6.89、6.39、6.82，第4日突增到7.45，但都在3类标准范围内，因此验证了该模型方法对突发事件预警的能力。排除4号点影响后，模型整体残差在两侧分布均匀，在-0.2与0.2之间，残差期望值接近于0。通过图1模型的正态Q-Q图检验，对应点分布在y=x附近，可以得出模型的残差值基本呈正态分布。进一步验证模型的构建是有效的。

2.共线性优化

首先可以对指标开展相关性检验，相关性检验可以检验指标之间是否存在明显的相关关系。根据相关性检验结果，相关性统计如表1。

所选指标中pH和浊度呈正相关，pH和氨氮呈正相关，溶解氧和氨氮呈负相关，浊度和氨氮呈负相关，因此所选指标存在共线性。且氨氮与其他3个指标存在明显的相关性，考虑先将氨氮作为待剔除指标，需进一步借助VIF与容忍度验证共线强度检验。根据R输出的结果如表2，在考虑剔除指标时，由于pH和氨氮存在较大的共线性关系，这也与实际相符，氨氮与水形成弱碱，氨氮的浓度越高，水中的pH值越大，因此优先考虑剔除其中一个指标，剔除指标方法结合显著性、容忍度、VIF（方差膨胀因子）进行判断。一般认为VIF大于10，容忍度小于0.1，说明自变量之间存在显著的共线性，这里将VIF较大的氨氮进行剔除。

VIF越大，容忍度越小，共线性越严重。将指标氨氮剔除后，重新建立模型，再次对模型进行容忍度和VIF检验，输出结果如表3，自变量容忍度均大于0.1，VIF小于10。新的模型R²变为0.9581，较之前无明显变化。

3.逐步回归验证

本文采用赤池信息量准则（AIC）进行逐步回归分析，得到最小AIC组合为：pH、溶解氧、浊度、电导率。最终表明无需再剔除指标，模型方程得到确认。

最终模型方程为：

y=1.576793-0.103860x₂+0.967248x₃-0.003806x₄+0.018848x₅

（二）拟合检验

通过对溶解氧的实测值与预测值的相对误差进行比较，以及y和yi之间的相对误差分析，根据图2曲线图可以看出，溶解氧实际值和预测值拟合度良好，拟合值和实测值呈显著的正相关性，说明多元线性回归模型具有较高的精准度，对历史值的预测较好。

五、结果验证

通过多元线性回归模型对水站2022年8月—12月每日溶解氧数据进行预测，得到预测值与实测值的拟合结果如图3所示，预测结果误差核密度如图4所示。

从相对误差核密度图可看出，多元线性回归预测平均相对误差近似为0.328%（接近于期望0），最大相对误差为14.5%，75%误差分位数为3.2%，90%分位数为5.4%，95%分位数为7.8%，即95%的情况下，误差精度在8%以内，说明多元线性回归模型满足水质预测预报的精度要求，模型预测效果较好，为水质预测预警提供了数据支撑。

六、结语

1.本研究利用水站历史自动监测数据，基于多元线性回归分析法，建立多元线性回归模型对溶解氧进行预测，结果表明，在此站点，多元线性回归模型对预测溶解氧浓度具有较高的精确度。

2.利用本研究建立的模型对水站2022年8月—12月每日溶解氧数据进行预测，验证数据显示模型满足水质预测的精度要求，预测效果较好，为水质预警预测提供了数据支撑。

3.该方法建模过程简单，结果直观，精确度高，大幅度减少了计算时间，可在其他断面推广和应用。

参考文献

[1]王婷婷，李慧.水质监测实验室的安全管理[J].资源与环境，2022，48（2）：190-192.

[2]张颖，高倩倩.基于灰色模型和模糊神经网络的综合水质预测模型研究[J].环境工程学报，2015，9（2）：537-545.

[3]石月.基于时间序列分析的松花江流域水质预测[D].哈尔滨：哈尔滨师范大学，2015.

[4]国务院.国务院关于印发水污染防治行动计划的通知[EB/OL].（2015-04-16）[2023-01-17] .http：//www.gov.cn/zhengce/content/2015-04/16/content_9613.htm.

[5]申杰，潘杨，黄勇.城市地表水环境评价方法综述[J].环保科技，2011，17（4）：41-45.

作者单位：中国人民大学