基于分数微分的时间序列相似性度量及其应用

闫汶朋 汪志涛 袁晓

摘 要    ：时间序列的相似性度量是时间序列聚类、分类以及其他相关时间序列分析的基础.传统基于距离的相似性度量方法，忽视了时间序列可能存在的时间上的联系，而将时间序列看作一系列孤立点的集合.对于序列间可能存在的前后联系，基于分数阶微分的遗传特性和记忆特性，提出一种新的时间序列聚类的相似性度量.根据时间序列的分数阶微分计算新序列间的点距离，将其作为聚类算法的输入对时间序列进行聚类.仿真实验结果表明，与基于原始序列矢量距离的聚类结果相比，新的分数阶相似性度量方法表现更好.

关键词 ：时间序列； 聚类； 相似性度量； 分数阶微分

中图分类号 ：TP391 文献标识码 ：A DOI ：  10.19907/j.0490-6756.2023.043004

Time series similarity measurement based on  fractional differential and its application

YAN Wen-Peng， WANG Zhi-Tao， YUAN Xiao

（College of Electronics and Information Engineering， Sichuan University， Chengdu 610065， China）

Similarity measures of time series are the basis for time series clustering， classification and other related time series analysis. The traditional distance-based similarity measure ignores the possible temporal connections of time series and treats time series as a series of isolated point sets. For the possible backward and forward connections between sequences， a new similarity measure for time series clustering is proposed based on the genetic and memory properties of fractional order differentiation. The point distances between the new sequences are calculated based on the fractional order differentiation of the time series， and then are used as the input of the clustering algorithm to cluster the time series. The simulation experimental results show that the new fractional-order similarity measure performs better compared with the clustering results based on the original distances.

Time series； Cluster； Similarity measure； Fractional differential

1 引 言

时间序列作为一种随时间顺序变化的数据序列，通常具有数据量大、维度高、无限递增、结构复杂等特点.近年来，面对日益庞大的时间序列数据集，人工标记的成本日益增加，属于无监督、半监督学习的时间序列聚类引起了越来越多研究者的兴趣，并被广泛应用于金融学  ［1］、医疗诊断  ［2，3］、工业生产控制  ［4］和生物学  ［5］等.聚类通过将相似的数据放入相关或同质的组中，将具有最小相似性的对象放入其他组中，已成为一种有用的数据分析方法.

对于时间序列的相似性研究，很多采用了欧几里德距离或其演变，但基于矢量的欧式距离及其演变单纯的将时间序列看做孤立点的集合，忽视了时间序列可能存在的时间上的联系和关键点信息，对于序列在时间轴上的偏移也非常敏感，不具备形态识别能力.针对这些问题，国内外学者们相继提出了众多的解决方法：广泛应用于语音识别领域的DTW  ［6］距离，通过把两个时间序列进行延伸和缩短，找到距离最短的扭曲距离；隐马尔可夫模型，利用时间序列隐含的属性（马尔可夫性）提高聚类精度.近年来，王瑞等  ［7］根据分段序列的斜率变化，划分形态模式，把时间序列转换成字符串序列.李海林等  ［8］提出动态时间弯曲与符号距离结合的时间序列距离度量方法，反映了时间序列数值分布和形态特征.Soleimani等  ［9］定义了两个相似性阈值并确定它们的值，提出了发展的最长公共子序列（Developed Longest Common Subsequence，DLCSS），解决了LCSS很难确定正确的相似度阈值，导致结果较差的问题.甄远婷等  ［10］基于中心Couple函数捕获时间序列的动态相依结构，采用Cramer-von Mises统计量构造了一种新的相似性度量.

本文提出一种基于分数阶微分的时间序列相似性度量，利用分数阶微分的遗传效应和记忆特性  ［11］，对原始时间序列数据进行分数阶微分计算，再根据传统的点与点距离公式计算得到相似度，最后将其作为聚类算法的输入完成时间序列的聚类.

2 分数阶微分理论基础

分数阶微积分作为一个重要的数学分支，近年来，已不断在科学、工程等领域得到了广泛的应用，并被引入控制论、流体力学、信号处理及图像处理等领域  ［12-18］.对于某些特定的应用，整数阶微分并不能进行很好的描述，需要借助分数阶微分以达到更精确的描述，如：流变本构方程、分数阶控制系统等.相对于整数阶微分，分数阶微分可以提供比整数阶微分更丰富的信息  ［19］.

2.1 G-L分数阶导数的定义

分数阶微分有多种不同的定义形式，适合于数值计算  ［20］的Grünwald-Letnikov（G-L）分数阶导数定义为

GL   a D  α tf（t）=  lim   η→0  A   （α） ηf（t），t∈ a，b   （1）

A    （α） ηf（t）=η   -α∑ ∞  j=0 g   （α） jf（t-jη）  （2）

g α 0=1，g α j= 1- α+1 j  g α  j-1，j=1，2，…  （3）

式（1）和式（2）中，D为分数阶微分算子； α （可取分数）为运算阶数； t 表示时间序列当前时刻； η 是采样步长；  g  （α）  j 为二项式系数，可通过式（3）递推求出.

可以看出，在计算分数微分时，要用到时刻 t 之前所有的历史数据，被加项数目变得非常大.对于时间序列，随着数据量的增大，考虑所有历史数据，分数阶微分的计算速度会随之受到影响，因此，在实际计算中，根据分数微分加权系数具有的较快衰减特性，使用短时记忆法则，只考虑时间序列当前时刻近来的过去，即在区间  t-L，  t  的行为.

GL   a D   α tf（t）≈  t-L D   α tf（t），t>a+L  （4）

式（4）中， L 是记忆长度.根据公式，具有下限 a 的分数导数可用具有移动下限 t-L 的分数导数来逼近.但是，这样的简化，在计算精度上会受到某些惩罚，对于 a≤t≤b ，若存在函数 f（t）≤M ，则可利用式（4），由短时记忆原理所引起的误差，建立估计.

Δ  =    GL   a D   α tf（t）-  t-L D   α tf（t） ≤ ML  -α   Γ  1-α   ，

a+L≤t≤b   （5）

该不等式可以用来确定给定精度 ε 情况下的记忆长度 L ，有

L≥   M ε  Γ  1-α       1 α    （6）

A -     （α） ηf（t）≈η   -α∑ J  j=0 g   （α） jf t-jη    （7）

式（7）中， J t-Jη≥0  表示计算 t 时刻序列点分数阶导数使用的非局域记忆点数，使用短时记忆原理，不考虑全部历史数据.

G-L定义适用于 α>0 和 α<0 的微分与积分，且当 α=0 时，有 D   0  if i =f i  ，在时间序列处理中，可将初始时刻 a 看为0.

2.2 G-L分数阶微分的数值计算

式（1）也可写为：    GL   a D   α tf（t）=A  （α） ηf（t）+ o  η  ，当选择的采样步长 η 足够小时，式（1）中的求极限操作可以忽略，G-L定义的分数阶导数便可以由     GL   a D   α tf（t）≈ A   （α） ηf（t） 直接计算，再结合短时记忆原理，减少计算过程.

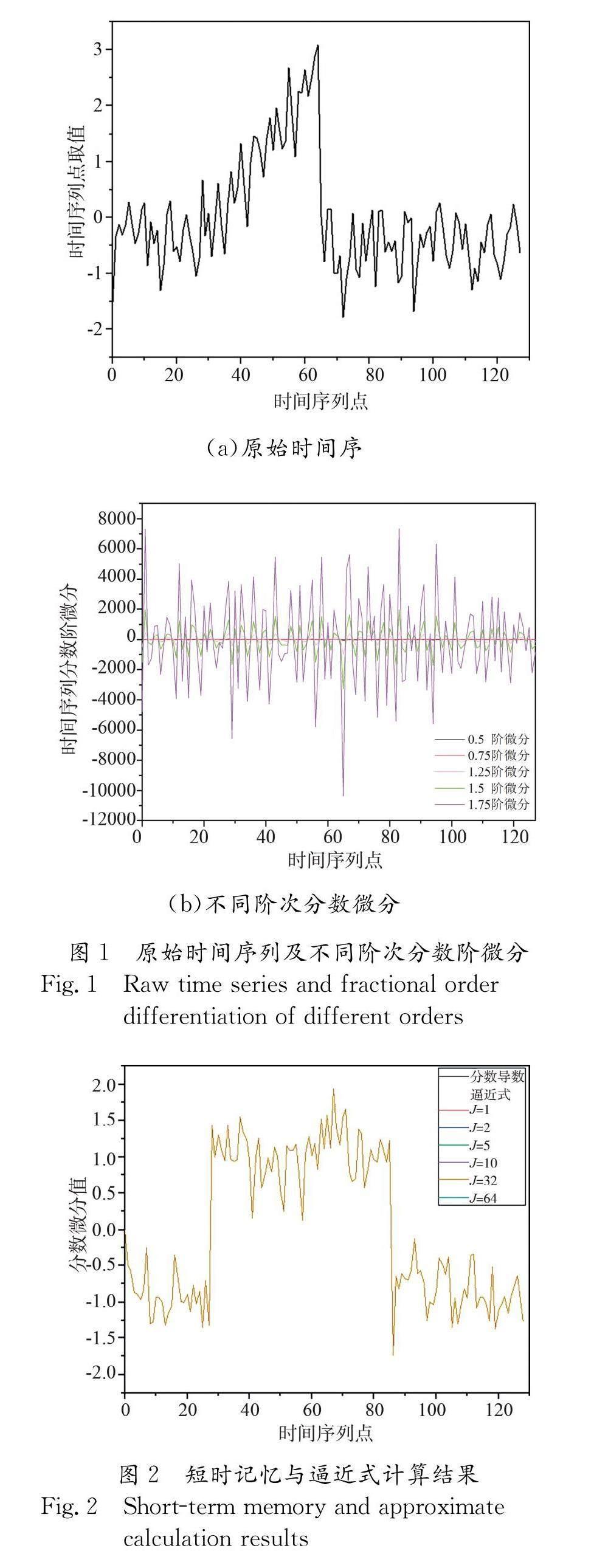
与传统的整数阶微分只使用当前和前几个有限步长内的函数值相比，分数阶微分具有遗传特性和记忆特性，涉及到 t 时刻序列点的前 J 个非局域记忆点序列值，可以捕捉时间序列的前后关系，与其他未将时间序列做相应计算，把各序列点看作孤立存在的方法相比，分数阶微分（如图1）考虑了时间序列的时间顺序，使时间序列相似性的刻画具有非局域的记忆特性.

对于精度损失的问题，对比了通过分数导数逼近式（1）与运用短时记忆原理计算式（7）计算结果的区别（CBF训练集， α  设置为0.01），如图2所示.可以看出，利用短时记忆原理，在不同记忆点数 J 的情况下，分数阶导数计算结果与逼近式计算结果接近完全重合，误差可忽略不计.

3  基于分数阶微分的时间序列相似性度量

给定两个长度为 n 的时间序列 x、y ，传统的欧式距离 d  E（ x，y ）=  ∑  n  i=1（x  i-y  i）   1/2 是时间序列聚类中最常用的相似度量.有研究表明，在时间序列分类精度上，欧式距离具有惊人的竞争力  ［21］，在诸多算法中都有广泛的应用.

时间序列由于具有先后顺序，把时间序列各点看做孤立的存在并不合理，因此，需要考虑时间序列中可能存在的时间上的联系，以达到更好的聚类效果.基于分数阶微分的时间序列相似度，对原始时间序列的每一点求其分数阶微分，可以看做计算一段序列的加权累计值.由于分数阶微分计算结果中某些数值较大，对其进行标准化处理，通过将所有数据与数据最小值的绝对值相加来转换数据，使数据的最小值变为0，其他所有数据变为正数，再使用Z-Score标准化处理数据.

D  ～  αx i=  D  αx i-μ σ   （8）

式（8），  x  i 表示时间序列的第 i 点数据；D  ～  αx i 表示时间序列各时间点的  α  阶分数微分； μ 表示分数阶微分时间序列的均值； σ 表示标准差；D  ～  αx i 表示分数阶微分时间序列各点标准化后的值.

算法1描述了具体过程.输入为时间序列各个时刻的函数值构造的向量，第（1）行设定初始化步长，（2）（3）行递推计算二项式系数，（4）～（8）根据相应的非局域记忆点数 J 计算给定时间序列的分数阶微分值，最后，标准化返回结果.

算法1   伪代码：分数阶微分

输入：  原始时间序列  T  i= t  1， t  2，…， t  n

输出：   标准化的分数微分时间序列

（1） 初始化 η

（2） for   j =2;  j   ≤ len （t）; j ++ do

（3）    ω← CalculateWeights（ ω ， α ）

end

（4） for  i  = 1;  i  ≤  len（ t ）;  i ++ do

（5）  if  i   ≥J  then

（6）    y ←CalFraDiff（ ω 1 ， f   1， h ， α ）

（7） else

（8）    y ←CalFraDiff（ ω 2 ， f   2， h ， α ）

end

（9） return Standardization（ y ）

再通过处理后的序列计算欧式距离得到相似度，定义如下.

d  α F（ x，y ）=（∑ n i=0 （ D  ～   ax  i- D  ～   ay  i） 2）  1/2=

（∑ n i=0 （A ～   α ηx  i-A ～   α ηy  i） 2）  1/2  （9）

式（9）， A α ηx i 和 A α ηy i 为时间序列各时间点的 α 阶分数微分计算表 达式（式2）； A ～  α ηx i 和 A ～  α ηx i 表示对其进行标准化； d α F（ x，y ）为最终计算得到的相似度.

4 实 验

编译工具Python3.9.8，操作系统Window11，CPU/AMD Ryzen 7 5800H with Radeon Graphics，主频3.20 GHz，内存16 GB，固态硬盘容量512 G.

4.1 实验数据与实验方法

本文实验中用到的时间序列数据集为UCR时间序列数据库  ［22］中收集的标准时间序列数据集，每个数据集包含一个训练集和一个测试集，具体信息如表1.

表1中， K 为聚类的数目; L 为时间序列的长度; N 为数据集的训练集数目; M 为数据集的测试集数目.

对于分数微分计算后的序列，在训练集上比较计算序列间欧式距离与改进的DTW距离LB_Keogh作为聚类输入的聚类准确度与时间消耗，如图3所示.

可以看出，计算两个序列间的欧式距离作为K-Means聚类的输入到完成聚类过程所需的时间远远小于LB_Keogh距离作为聚类输入所需的时间，且随着时间序列数据量的增大，时间差异更加明显.在聚类准确度方面，两种距离互有优劣，因此，综合考量时间与准确度因素，选择欧氏距离作为计算处理后序列间相似度的距离公式.

实验总体采用不同的距离度量，并通过K-Means聚类算法实现对时间序列的聚类，同时也采用了层次聚类与基于u-shapelets的时间序列聚类算法  ［23］进行相关实验，最后对所得结果进行对比分析.分数微分欧式（Fractional Differentiation Euclidean， FDE）距离首先对数据集中的时间序列进行 α 阶分数微分运算，将其标准化后，再根据运算后序列的欧式距离计算得到两个时间序列的相似度，以此作为聚类算法的输入完成聚类，并使用 R （Rand Index）评价聚类质量.

R= a+d a+b+c+d   （12）

式（12）中， a 为在实际类别中为同一类且在聚类结果中也为同一类的数据点对数; d 为在实际类别中不为同一类且在聚类结果中也不属于同一类的数据点对数; b 为在实际类别中为同一类但在聚类结果中不属于同一类的数据点对数; c 为在实际类别中不为同一类但在聚类结果中属于同一类的数据点对数.

计算相似度时，记忆点数 J 和阶数 α 的不同将会影响距离度量，并最终影响聚类质量.图4给出了单独的不同 J 、  α 分别对于聚类质量评价的影响.通过将式（6）计算得到的距离作为聚类算法  ［24］的输入，获得了两个变量 J、  α 对聚类质量的影响（如图5）.

为了确定最佳 J 、 α 值，本文通过在训练集中，观察不同 J 和 α 对于聚类质量评价 R 的影响，再在测试集中，利用训练集得到的最佳 J  、α 进行多次实验取均值得到最终结果.

4.2 实验结果分析

4.2.1 准确度对比  对基于LB_Keogh距离、欧式距离、余弦距离、Pearson相关系数的K均值聚类、层次聚类  ［25］、基于u-shapelets的时间序列聚类结果比较如表2所示，其中， J 、 α 分别为获得的最佳记忆点数与分数阶导数的阶数，Win一行标明了采用5种不同的距离度量和聚类算法在21个数据集上取得最佳效果的数量.

从表2可知，在21个时间序列数据集中，本文提出的FDE距离分别在14个数据集、14个数据集、15个数据集、16个数据集上优于基于余弦距离、LB_Keogh距离、欧氏距离、Pearson相关系数的K-Means聚类，在16个数据集上优于层次聚类的结果，14个数据集上优于基于u-shapelets的时间序列聚类.实验表明，虽然在不同的数据集上，基于各种距离的K-Means聚类、层次聚类和基于u-shapelets的时间序列聚类算法都能或多或少取得最佳的聚类效果，但是本文所提出的方法整体效果最佳.

4.2.2 运行时间对比  欧式距离、DTW距离是常用的基于距离来衡量相似性的指标.FDE在欧氏距离的基础上，增加了分数微分的计算过程，对比FDE与此两种距离作为K-Means聚类算法的输入，并比较了层次聚类与基于u-shapelets的时间序列聚类算法在10个时间序列数据集上完成聚类操作所需的时间.结果如表3所示，可以看出，FDE在运行时间上逊于基于欧几里得距离的K-means聚类与层次聚类，大幅优于基于LB_Keogh距离的k-means聚类和基于u-shapelets的时间序列聚类，具有更高的时间效率.

5 结 论

为了解决传统的基于距离的相似性度量方法将时间序列矢量看作孤立点存在的问题，本文提出利用时间序列的分数阶微分构造新的时间序列，用构造的新序列间的欧式距离计算相似度作为K-Means聚类算法的输入完成聚类过程.

通过与基于传统距离度量的K-Means聚类、层次聚类以及基于u-shapelets的聚类结果进行比较，可以得出，本文方法相对于欧式距离简单快速的实现方式，牺牲了一些计算速度，在一定程度上提高了聚类准确度.

后续研究中，我们可考虑以下两个方面：（1） 对于时间序列先计算分数阶微分，再计算点距离计算时间较长的问题，可考虑第二次计算过程使用符号聚合近似、主成分分析等数据降维和特征表示方式来计算相似度，减少计算过程，以加快计算速度；（2） 利用深度学习，对获得的新序列进行特征提取、距离矩阵计算的自适应权重等方式，以得到的更好的聚类结果.

参考文献：

［1］   Ruiz E J， Hristidis V， Castillo C，  et al . Correlating financial time series with micro-blogging activity  ［C］∥Proceeding of the fifth ACM International Conference on Web Search and Data Mining. New York： ACM， 2012： 513．

［2］  Li G， Braeysy O， Jiang L，  et al . Finding time series discord based on bit representation clustering［J］. Knowl-Based Syst， 2013， 54： 243.

［3］  Tavenard R， Malinowski S. Cost-aware early classification of time series ［C］//Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Cham： Springer， 2016.

［4］  Zalewski W， Silva F， Maletzke A G，  et al . Exploring shapelet transformation for time series classification in decision trees ［J］. Knowl-Based Syst， 2016， 112： 80.

［5］  Jiang D， Pei J， Ramanathan M，  et al.  Mining gene-sample-time microarray data： a coherent gene cluster discovery approach ［J］. Knowl Inf Syst， 2007， 13： 305.

［6］  Salvador S， Chan P. Toward accurate dynamic time warping in linear time and space ［J］. Intell Data Anal， 2007， 11： 561.

［7］  王瑞， 贾瑞玉. 基于形态模式的时间序列相似性度量算法［J］.计算机应用与软件， 2017， 34： 253.

［8］  李海林， 梁叶.基于数值符号和形态特征的时间序列相似性度量方法［J］.控制与决策， 2017， 32： 451.

［9］  Soleimani G， Abessi M. DLCSS： a new similarity measure for time series data mining［J］.Eng Appl Artif Intel， 2020， 92： 103664.

［10］  甄远婷， 冶继民， 李国荣.基于中心Copula函数相似性度量的时间序列聚类方法［J］.陕西师范大学学报： 自然科学版， 2021， 49： 29.

［11］ 袁晓.分数微积分—理论基础与应用导论［M］.北京： 电子工业出版社， 2021.

［12］ Huang J， Li H， Chen Y Q，  et al . Robust position control of PMSM using fractional-order sliding mode controller ［C］//Abstract and Applied Analysis. Hindawi： ［s.n.］， 2012.

［13］ 伍小二.一类无界变差函数的分数阶微积分及其分形维数［D］.南京： 南京理工大学， 2018.

［14］ 徐明瑜， 谭文长．中间过程、临界现象—分数阶算子理论、方法、进展及其在现代力学中的应用［J］．中国科学Ｇ辑： 物理学 力学 天文学， 2006，  36： 225.

［15］ 蒲亦非， 袁晓， 廖科， 等．现代信号分析与处理中分数阶微积分的五种数值实现算法［J］．四川大学学报： 工程科学版， 2005， 37： 118.

［16］ 杨柱中， 周激流， 晏祥玉， 等.基于分数阶微分的图像增强［J］.计算机辅助设计与图形学学报， 2008， 20： 343.

［17］ 陈卫卫， 王卫星， 闫迪. 基于分数阶微分Frangi的夜间车道线检测［J］.四川大学学报：自然科学版，2021， 58： 022001.

［18］ 彭朝霞， 蒲亦非. 基于分数阶微分的卷积神经网络的人脸识别［J］.四川大学学报：自然科学版， 2022， 59： 012001.

［19］ 薛定宇.分数阶微积分学与分数阶控制［M］.北京：科学出版社， 2018.

［20］ 周宇， 袁晓， 张月荣. 基于IFFT的Lubich数字分数微分器系数的快速算法［J］.太赫兹科学与电子信息学报， 2022， 20： 608.

［21］ Lkhagva B， Yu S， Kawagoe K. New time series data representation ESAX for financial applications［C］// International Conference on Data Engineering Workshops. Atlanta： IEEE Computer Society，  2006.

［22］ Dau H A， Keogh E， Kamgar K，  et al . The ucr time series classification archive ［EB/OL］. ［2022-05-22］. https：//www.cs.ucr.edu/eamonn/time series data 2018.

［23］ 余思琴， 闫秋艳， 闫欣鸣. 基于最佳u-shapelets的时间序列聚类算法［J］.计算机应用， 2017， 37： 2349.

［24］ 李海林， 张丽萍.时间序列数据挖掘中的聚类研究综述［J］.电子科技大学学报， 2022， 51： 416.

［25］ 陈美云.时间序列聚类分析中几种算法的研究及应用［D］. 徐州： 中国矿业大学， 2019.