复虹现象的实验研究
彭子云 漆元臻 李泽宇 梁颖 向红 韩德专


摘 要 彩虹是一种常见的大气光学现象,在一定天气条件下,在彩虹的附近还会出现附加的弧形彩色条纹,这就是复虹。目前关于复虹的实验研究还十分有限。本文从集体散射与单体散射两方面对复虹现象进行了实验研究。通过水雾光散射再现了复虹现象,并测量统计了水滴尺寸及其分布对复虹的影响。然后通过单水滴光散射实验,研究了不同照明波长、不同水滴尺寸下的复虹现象,从微观上解释了复虹的形成机理。我们还利用散射理论计算研究了水滴尺寸及其统计分布对复虹效果的影响,计算结果进一步证实了实验结论的正确性。
关键词 复虹;水滴尺寸分布;色散;米氏散射
彩虹是一种常见的自然现象,在古代人们就对其做出了各种解释,而对于彩虹的科学研究则开始于近代。17世纪,笛卡尔提出彩虹是光在水滴内的反射与折射的结果,并运用几何光学成功计算了虹与霓的角度,但未能解释色彩的成因。
后来牛顿提出了色散理论,彩虹这一光学现象得到了较好的解释[1,2]。人们还注意到在一定天气条件下,在彩虹的附近还会出现附加的弧形彩色条纹,即复虹[1,3](Supernumerary rainbows)。几何光学理论无法解释这一现象。1803 年,托马斯·杨将复虹解释为两角度相同的光束干涉的结果,但该理论与实际现象存在差异[1,3]。1838年,艾里(Airy)提出了“彩虹积分”,更加完备的解释了复虹现象[1,4,5]。1908年,Gustav Mie提出米氏散射理论,即通过求解麦克斯韦方程组来得到包括均匀球体在内的物体对光的散射的严格解。这样,彩虹以及复虹现象,可以被准确地计算出来[1,6,7]。迄今为止,关于复虹的研究主要集中在理论分析与模拟计算上,例如利用散射理论分析复虹现象及影响因素[8-10],而实验方面的研究则非常有限。本论文将从集体散射与单体散射两方面对复虹现象进行实验研究,结合理论计算对复虹现象及影响因素给出清晰直观的解释。
1 复虹现象简介
彩虹是光线被水滴散射时发生的一种色散现象[10]。从几何光学的角度来看,光线进入水滴后会发生多次反射与折射。此过程中,不同位置的入射光线对应不同的入射角,因此出射角度也不同。再由于色散,同一位置入射但波长不同的光线出射角度也不同,从而形成色彩分布。当光线在水滴内反射一次就折射出来时,以40~42度的视角内光最为强烈,形成我们常见的一级虹。如果在光水滴内发生两次反射再折射出来,则以50~53度的视角内光最为强烈,形成二阶彩虹,即通常所说的霓。
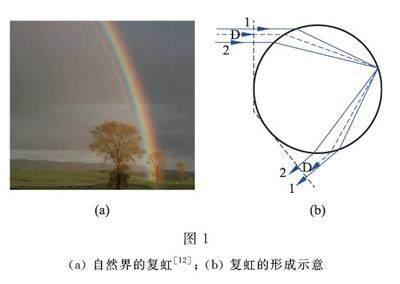
光作为一种电磁波,其波动性会在一定条件下表现出来,例如干涉与衍射现象。相应的,在一定条件下,彩虹中也会出现干涉现象,例如复虹现象。图1(a)展示了具有复虹结构的彩虹。如图所示,在彩虹的内侧存在多层弧形的彩带,这些彩带被称为复虹。严格解释复虹现象需要用米氏散射理论,但是不够直观。用托马斯·杨的观点来看,复虹的形成可以解释为水滴中传播路径相近的光线之间的干涉现象。图1(b)中,光线D代表笛卡尔光线,即偏向角最小的光线,对应观察到的主虹。光线1与2为邻近的两条光线,他们在出射时也保持平行。这两条光线在远端(观察者位置)发生干涉,形成了条纹,白光照射时则形成彩色条纹,即复虹。由于光程差依赖于水滴的尺寸,因此复虹现象与水滴的尺寸及分布都有关系。当水雾中的水滴尺寸差异很大时,各个水滴形成的条纹的角分布不同,在非相干的叠后,条纹对比度会下降。因此只有在合适的条件下才能观察到复虹现象。一般来说,水滴尺寸越小,形成的干涉条纹越宽,由条纹错位叠加产生的填补效应就越不明显。
同时,水滴尺度的分布越集中,条纹填补效应则越弱,也就更容易观察到复虹。
2 复虹再现与水滴分布测量
为了研究复虹现象,我们采用了投影仪作为白光光源,菲涅尔透镜作为准直元件来产生平行光,如图2(a) 所示,此方案可以获得横截面积较大而且平行度较好的光束。在观察彩虹现象时,利用压力喷壶在菲涅尔透镜后喷水雾,在光源一侧即可看见虹与霓。通过改变喷壶内压强以及喷嘴的松紧,可以改变水滴的尺寸及分布。当压力较大且喷嘴较紧时,在主虹的内侧或霓的外侧,还能看到一系列明显的弧形彩带,即复虹,如图2(b)所示。当减小喷壶压力或拧松喷嘴时复虹逐渐消失。图2(c)以透视画法示意了复虹的拍摄方位及效果。投影仪发出的光经菲涅尔透镜准直后形成矩形横截面的平行光束。照相机位于菲涅尔透镜的左上方,在此位置上,看到矩形的光束向远处传播汇聚到无穷远处一点。光在喷雾区发生散射,形成以观察者(照相机)为中心的彩色圆弧。由于立体透视效应,拍摄的虹与霓具有锥状轮廓。照片中左下和右上的三角区域因没有光照而呈现出黑色。我们利用分光计测量了虹与霓的角度。实验中,分光计距离喷雾约1m。测量结果表明,虹处于40~42 度,霓处于50~53 度,与公认值一致。
为 了测量统计水滴的尺度分布,我们利用浸入法测量了复虹现象显著与复虹刚好消失这两种情况下对应的水滴尺度。实验过程如下:首先将盛有植物油的培养皿置于水雾处,开始用挡板遮盖;然后喷雾,当观察到彩虹时快速移走挡板,让培养皿接收水滴,再快速遮盖住培养皿。最后将培养皿缓慢移至读数显微镜下进行测量。
我们对复虹最显著和复虹刚好消失這两种情况下的水滴进行了随机测量,每组样本数量为160,并以0.02mm 的间隔进行统计,结果如图3所示。图中横轴表示直径,纵轴代表水滴数量。
我们尝试了正态分布和对数正态分布来拟合水滴尺寸的分布。对于复虹显著的情况,对数正态分布更合适。对于复虹刚好消失的情况,水滴直径分布更符合正态分布。由于统计方法不同,我们以半高全宽作为弥散程度的统计指标。由图可知,当复虹现象明显时,水滴尺寸较小且分布相对集中;而当复虹刚好消失时,对应水滴尺寸较大且分布相对弥散。
3 单水滴光散射实验
为了研究复虹产生的微观机理,我们测量了单个水滴对光的散射,考查同一水滴对不同波长的光的散射以及在单色光照明下不同尺寸的水滴的响应。实验系统如图3所示。该装置的核心是分光计,其中平行光管的缝光阑被改装为小孔光阑。激光(本实验采用红、绿、蓝激光笔)经过衰减片后照射到透镜上,再聚焦到平行光管的光阑处,然后经平行光管的准直透镜后准直为宽截面的平行光出射。单个水滴由注射器产生,水滴的直径由读数显微镜来测量。激光束照射到水滴后反生散射,用白屏接收,可以看到环形的条纹,这即是单个水滴的光散射现象。图4展示了局部的散射条纹。转动望远镜对准这些条纹,可以准确测量对应的角度。然后将望远镜转开,将线阵CCD置于刚才望远镜的位置,则将这些条纹的光强分布记录下来。
图4展示了同一水滴(直径为2.012mm)在蓝光(450nm)、绿光(533nm)与红光(654nm)照明下的散射光强随观察角度的变化。图中的曲线是CCD探测到的光强信号,其角度信息由分光计测得。这里散射光强做了归一化处理。曲线的上方是对应的散射条纹的局部照片。这些曲线的左侧主峰对应常规观测到的虹,右侧的主峰则对应霓,即二级虹。这里是单色光的散射,不是通常意义上的虹与霓,但是为了方便描述,下面仍以“虹”和“霓”来称呼。“虹”与“霓”之间有一个暗区,这就是所谓的亚历山大暗带。显然,随着波长的增大,“虹”与“霓”都向中间移动,亚历山大暗带变窄。
而在“虹”的左侧与“霓”的右侧,还有一系列条纹,这就是单色光的“复虹”。可以看出,波长越小,条纹越密集。
图5 展示了不同尺寸的水滴在红光(波长654nm)照明下的散射光强随观察角度的變化。
由于散射光强会随着水滴尺寸的减小而迅速减弱,再加上“霓”的散射光强比“虹”的散射光强更弱,因此对小尺寸单水滴“霓”部分的探测变得困难,我们这里只给出“虹”对应的散射光强。由图可知,随着水滴尺寸减小,“虹”的主峰会向角度减小的方向偏移,同时干涉条纹也展宽,这与其他文献报道的研究结果一致[13]。散射效果对水滴尺寸的依赖进一步体现了光的波动性对彩虹现象的影响。因为按照几何光学理论,虹的主峰的角位置与水滴尺寸无关。当然,要进一步搞清楚干涉条纹如此分布的原因,需要定量研究入射光经过水滴之后的波前变化。这可以通过干涉实验来实现,例如让经水滴出射的光与一束平面波进行干涉,根据干涉图样来获取相关波前的变化。
从上面的实验可以看出,单个水滴的光散射既依赖于照明波长,也依赖于水滴的尺寸。对波长的依赖,即色散效应,使得水雾的光散射形成彩色的虹与霓。而对水滴尺寸的依赖,则对复虹的观察效果产生很大影响。不同尺寸的水滴形成的散射条纹的角位置与角宽度都不同,这些条纹的非相干叠加会使得条纹对比度下降。在前面的图2 所示的实验中,水滴尺寸小且分布集中时,复虹现象明显,而水滴尺寸增大且分布弥散时,复虹减弱至消失。这是因为,水滴尺寸越小,条纹宽度越大,越有利与观察。另一方面,尺度分布越集中,条纹间的错位越小,对比度越高。同时,由于小水滴的干涉条纹宽,对于尺度弥散导致的条纹错位容忍度更高。因此,水滴尺度小且分布集中的水雾容易观察到复虹。
4 米氏散射计算
对于自然界中形成的虹与霓以及复虹现象,波长和水滴尺寸都是连续分布的。我们目前的实验条件还无法进行相关研究。这里,我们利用米氏散射理论来计算分析波长分布和水滴尺寸分布对复虹现象的影响。米氏散射理论利用多极辐射理论来求解散射问题,是严格可靠的计算方法并广泛应用于散射问题。这里我们采用一个基于米氏散射理论的开源程序[6]来进行相关计算。下面我们考虑尺寸满足正态分布的水滴的集体散射行为,我们只给出“虹”一侧的结果。
首先我们考虑在单色光照明(波长为650nm)下,分布参数对散射结果的影响。在图6(a)中,水滴尺寸分布的标准差SD 都为10%,但平均尺度不同。可以看出,随着尺寸的增大,这些散射峰的角度分布更加集中。例如,当水滴平均直径由0.12mm 增大到0.24mm及0.96mm时,40度附近的主峰与最邻近次峰的角距离则由3.1度减小到1.9度及0.76度。图6(b)是平均直径相同(d =0.12mm)但分布不同的水滴散射情况。由图可以看出,当水滴分布较集中时,可以看到明显的复虹;而水滴分布弥散时,复虹的对比度减弱以至于消失。
我们然后计算了复色光照明时的波长叠加效果。图7(a)展示了尺度正态分布的水雾(平均直径为0.6 mm、标准差SD=10%)在不同数量的波长照射下的散射强度以及彩虹效果。我们在380~700nm 范围内等间隔取N 个波长,并基于CIE1931XYZ色彩空间标准[14]合成了颜色。图中曲线代表散射光强及合成颜色,上方的条形彩图给出了视觉效果。可以看出当波长数目N =3时,叠加出来的虹的内侧有彩色条纹。波长数目增加至10时,虹内侧的条纹光强对比度明显下降,从视觉效果上看,“复虹”就不太明显了。当波长数量增加到100后,其效果与N=10的情况差异不大。
作为对比,图7(b)展示了在白光 (380~700nm,100个波长) 照射下,散射效果随平均直径的变化。这里水滴尺寸的标准差SD 都为10%。可以看出,水滴尺寸越小,条纹对比度越高,复虹效果越明显。
这里的计算结果表明:(1)单色光照明时,无论大小水滴都会产生对应于复虹的散射条纹,但尺寸越大,条纹越密集;(2)水滴尺寸分布越弥散,对应于复虹的散射条纹越不明显;(3)白光照明时,多波长的叠加效果是:尺度越小条纹越明显,分布越集中条纹越明显。这与之前的实验是一致的。
5 结语
本文对复虹现象的形成原因以及影响因素展开了系统的研究。我们在宏观上实验观测了复虹现象并统计了对应的水滴尺寸分布,发现水滴尺寸小且分布集中时复虹现象更明显,而尺寸较大且分布弥散时复虹现象减弱以至于消失。为了研究复虹现象的形成机理及影响因素,我们实验测量了单个水滴在单色光照射下的散射行为,获得了散射光的角度分布及强度信息,得到照明波长、水滴尺寸等对虹与霓及其复虹的影响。同时我们还利用米氏散射理论进行了定量计算,进一步说明了水滴大小,尺寸分布以及多波长叠加对复虹的视觉效果的影响,理论分析与实验结果一致,合理解释了复虹的形成机理及影响因素。
参 考 文 献
[1] HULST H C. Light scattering by small particles[M]. New York: Dover Publications, 1981.
[2] ALEXANDER H. Rainbows in nature: Recent advances in observation and theory[J]. European Journal of Physics,2016,37(6):1-1.
[3] LAVEN P. Supernumerary arcs of rainbows: Youngs theory of interference[J]. Applied optics, 2017, 56(19): 104-112.
[4] OUELLETT P E. Supernumerary bows: interference theory with the zero wavefront as a basic element[J]. Journal of the Optical Society of America A-Optics Image Science and Vision, 2019, 36(7): 1162-1172.
[5] OUELLETTE P E. Supernumerary bows: caustics of a refractive sphere and analysis of the relative overall Gouy phase shift of supernumerary rays[J]. Applied optics,2019,58(3):712-722.
[6] LAVEN P. Simulation of rainbows, coronas and glories using Mie theory and the Debye series[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2004, 89(1-4):257-269.
[7] 韓凯,许晓军.基于散射模型的霓虹现象研究[J]. 激光与红外, 2016,46(3):334-339.
[8] FRASER A B. Why can the supernumerary bows be seen in a rain shower[J]. Journal of the Optical Society of America,1983, 73(12): 1626.
[9] SHAN X, XIAHOU C K, CONNOR J N L. Rainbows, supernumerary rainbows and interference effects in the angular scattering of chemical reactions: an investigation using Heisenbergs S matrix programme[J]. Physical Chemistry Chemical Physics, 2018, 20(2): 819-836.
[10] XIAHOU C K, SHAN X, CONNOR J N L. Rainbows,supernumerary rainbows and interference effects in the angular scattering of chemical reactions: Effect of varying the modulus of the S matrix in the context of Heisenbergs S matrix programme[J]. Physica Scripta,2019,94(6).
[11] 余虹.彩虹与色散[J].物理与工程, 2017,27(2):22-25.
[12] Kim. A Perfect Rainbow[DB/OL]. 2018.9.12. https://writinginnorthnorfolk.com/2018/09/12/a-perfect-rainbow/.
[13] WALKER J D. Multiple rainbows from single drops of water and other liquids[J]. American Journal of Physics,1976, 44(5): 421-433.
[14] CIE (1932). Commission internationale de lEclairage proceedings[C]. Cambridge: Cambridge University Press,1931.

