摇臂轴助力式循环球EPS系统的控制策略

胡鹏 龚伟 谢刚 钟良 廖俊富 李刚

摘要：设计了一种摇臂轴助力式循环球EPS系统，采用滑模控制方法设计系统控制器。在考虑了二级减速机械结构磨损的基础上，建立EPS系统的状态方程，并根据滑模控制理论求出EPS系统的切换函数，然后采用一种优化后的指数趋近律来限制切换函数的1阶导数。通过MATLAB/Simulink建立EPS系统动态模型并仿真，结果表明滑模控制下的EPS系统跟随性好、超调量小，且有效削弱了滑动模态切换引起的抖振。研究结果可供新能源汽车转向系统的设计与开发参考。

关键词：EPS系统滑模控制趋近律抖振

中图分类号：U463.4文献标志码：A文章编号：1671-8755（2023）01-0075-09

Abstract：EPSsystemwithrockershaftassistedcirculatingballwasdesigned，andtheslidingmodecontrolmethodwasusedtodesignthesystemcontroller.Onthebasisofconsideringthewearofthemechanicalstructureofsecondaryreducer，thestateequationoftheEPSsystemwasestablished，theswitchingfunctionoftheEPSsystemwasobtainedaccordingtotheslidingmodecontroltheory，andthenanoptimizedexponentialapproachlawwasusedtolimitthefirstderivativeoftheswitchingfunction.ThedynamicmodelofEPSsystemwasestablishedandsimulatedbyMATLAB/Simulink.TheresultsshowthattheEPSsystemunderslidingmodecontrolhasgoodfollowingperformanceandsmallovershoot，andeffectivelyweakensthechatteringcausedbyslidingmodeswitching，whichcanprovideareferenceforthedesignanddevelopmentofthesteeringsystemofnewenergyvehicles.

Keywords：EPSsystem;Slidingmodecontrol;Approachlaw;Chattering

循環球EPS系统由转向器机械结构、助力电机、减速器、离合器和电子控制单元等组成。在系统的控制过程中，电子控制单元接收来自各传感器的信号并进行分析，再根据控制策略给出控制信号，实现预期助力目标，控制车辆稳定转向［1］。21世纪清洁能源的快速发展为汽车EPS系统的设计研发提供了无限可能［2］。在对汽车EPS研发的过程中，出现了许多可参考的控制方法。李耀华等［3］考虑路面附着系数的影响，将基于模糊控制的电流补偿控制策略与基于转向阻力矩的控制策略对比发现，前者具有更好的转向轻便性。商显赫等［4］基于DSpace的试验台架进行EPS系统试验验证，得出滑模控制策略远比PID控制策略的超调量小，能够实现对目标电流的实时跟随，并提高系统的鲁棒性。李洪强等［5］对常规PID控制和基于粒子群算法的PID控制进行了仿真对比，发现基于粒子群算法的PID控制策略系统响应时间更快，趋于稳定所用时间更短。商显赫等［6］采用基于BP神经网络的PID自适应控制，实现了PID算法参数的自整定、EPS系统在助力模式下的转向轻便性和对目标电流较好的跟随性。王燮辉等［7］基于MATLAB/Simulink和DSpace搭建C-EPS硬件在环仿真平台，实现了主动回正功能和C-EPS的主观评价，并能及时发现C-EPS在软硬件上的不足之处。孟令广等［8］针对实验改装的城市电动物流车的EPS系统，采用模糊PID控制在不同车速下进行系统仿真，验证了模糊PID控制比传统PID控制具有更好的转向控制性能。汪洪波等［9］将可拓模糊切换控制与模糊切换控制、直接切换控制进行系统仿真对比，发现可拓模糊切换控制具有更小的切换冲击和更高的切换平稳性，实现了EPS多模式的平滑切换。翁敬良等［10］采用H∞鲁棒控制对路感仿真结果、EPS系统的助力特性和操纵稳定性进行分析，发现基于H∞混合灵敏度控制的EPS系统有助于提高车辆转向时的轻便性以及操纵稳定性。赵万忠等［11］提出了“上层混合H2/H∞电流决策控制+下层模糊PID电流跟踪控制”的控制策略，实现了EPS系统对路面低频信息的有效获得和对高频干扰的抑制。晋兵营等［12］用遗传算法离线优化法对TSK型模糊控制器进行优化，实现了对电动机目标电流在负载变化和噪声干扰下的准确、快速跟踪。

本文设计了一种摇臂轴助力式循环球EPS系统，采用滑模控制来设计系统控制器。通过MATLAB/Simulink建立EPS系统动态模型并进行仿真，验证方法的有效性和可行性。

1EPS系统动力学模型

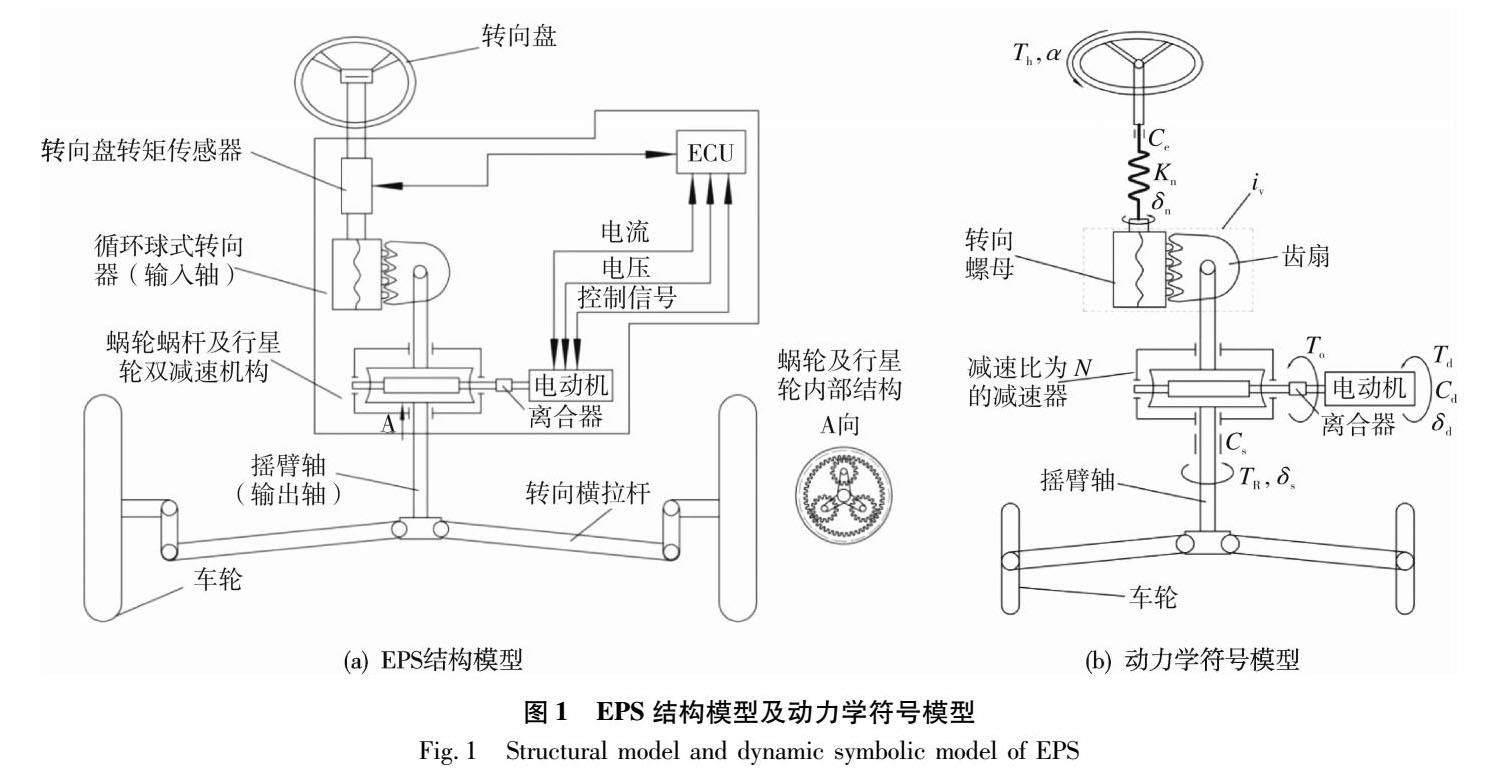
为满足公共服务领域的商用新能源客车和大吨位新能源载重汽车的使用要求，设计了一种创新的摇臂轴助力式循环球转向器。此转向器的助力机械结构安置在摇臂轴处，助力电机经此结构二级减速后对摇臂轴输出扭矩，完成助力。在转向系统进行助力时，因为是对输出端（摇臂轴）直接助力，所以经过的传动链少，减少了能量的消耗并能提供更大的助力。这种新型摇臂轴助力式EPS系统的结构模型如图1（a）所示，其动力学符号模型图如图1（b）所示。

3.1无控制下的仿真

在系统处于无控制状态时，观察式（3）中输入量Th，TR分别为单位阶跃信号时的输出响应。在MATLAB/Simulink中建立其动力学模型并仿真，得到扭矩响应结果如图3所示。

由图3可以看出，对阶跃输入，系统在0.2s内就能到达平衡状态，但到达平衡状态前的振荡衰减过程会对车辆转向控制造成一定影响。如扭杆扭矩Tn响应曲线表现为高频低幅振荡，衰减时间约为0.16s，这将使EPS系统产生异响，转向不平稳，驾驶员会感到非常不舒服。对于高速运动的车辆转向控制而言，0.2s太久，在各种因素的作用下，系统极有可能会产生滞后和过冲现象，导致车辆在遭遇突发状况时的响应完全可能耗时更长。因此，这样的性能表现完全不能满足EPS系统的快速跟随性和稳定性要求。因此，需要对EPS系统人为施加控制以提升系统品质。

3.23种控制律下的仿真

取初始值X=［0.1，0，π，0］T，物理含义为取方向盘转角及角速度分别为0.1rad，πrad/s，取摇臂轴转角及角速度分别为0rad，0rad/s。对式（17）、式（18）两种指数趋近律均取ε=diag［10，10］，式（17）、式（18）、式（19）3种指数趋近律均取k=diag［1000，1000］，当k取此值时，经计算得式（19）的ε=diag［0.001，0.001］。再运用MATLAB/Simulink对系统建模并仿真，得到上述3种控制律作用下方向盘转角运动情况和摇臂轴转角、扭杆扭矩对滑模控制下的响应仿真结果如图4所示。

本文EPS系统中，方向盘转角α对应图4中纵坐标x1，摇臂轴转角δs对应图4中纵坐标x2，扭杆扭矩对应图4中纵坐标Tn。由图4可以看出，方向盘转角、摇臂轴转角和扭杆扭矩在0.01s内均到达平衡状态。相比之下，系统平衡后，图中除代表常用趋近律的黑实线有抖振外，文献［16］趋近律和优化趋近律的蓝虚线和黄点线经放大后仍观测不到抖振。

由图4可知，方向盘转角、摇臂轴转角和扭杆扭矩到达平衡位置后均为零，这说明系统平衡后，方向盘和扭杆回到了同一轴线上，故而扭杆从扭转状态回到了非扭转狀态。因此，转角传感器和扭矩传感器的测量均为零，但对于整车车体而言，方向盘实际上转过了相应角度。本文EPS系统在3种趋近律作用下，超调量均很小，几乎实现了无超调。其中，使EPS系统接近平衡状态最快的是优化趋近律。相比之下，优化趋近律不仅能够缩短系统非滑动模态段的时间，而且能够比常用趋近律和文献［16］趋近律获得更好的动态品质，综合性能最好。

3.3不同ε值下的仿真

同样取初始值X=［0.1，0，π，0］T，对优化趋近律中ε分别取ε=diag［10，10］，ε=diag［100，100］，ε=diag［1000，1000］，k均取k=diag［500，500］，运用MATLAB/Simulink对系统建模并仿真。根据上述3个不同的ε值，得到本文所用指数趋近律作用下的方向盘转角运动情况和摇臂轴转角、扭杆扭矩对滑模控制下的响应仿真结果如图5所示。

由图5可以看出，方向盘转角、摇臂轴转角和扭杆扭矩均能在0.01s内到达平衡状态，且平衡后将图形放大，观测到本文EPS系统在3个不同的ε作用下均有抖振，且ε越大抖振越大，观测到摇臂轴转角和扭杆扭矩出现了明显超调。

3.4不同k值下的仿真

同样取初始值X=［0.1，0，π，0］T，对优化趋近律中ε均取ε=diag［10，10］，k分别取4个值：k=diag［100，100］，k=diag［300，300］，k=diag［500，500］，k=diag［1000，1000］，运用MATLAB/Simulink对系统建模并仿真。根据上述4个不同的k值，得到优化趋近律作用下的方向盘转角运动情况和摇臂轴转角、扭杆扭矩对滑模控制下的响应仿真结果如图6所示。

由图6可以看出，当取k=diag［500，500］和k=diag［1000，1000］时，方向盘转角、摇臂轴转角和扭杆扭矩均能在0.01s内达到平衡状态；当取k=diag［300，300］时，方向盘转角、摇臂轴转角和扭杆扭矩大约在0.04s达到平衡状态；当取k=diag［100，100］时，方向盘转角、摇臂轴转角和扭杆扭矩大约在0.10s达到平衡状态。平衡后将图形放大，观测到本文EPS系统在4个不同的k作用下均有抖振，且k过大也会导致抖振增大；k越大超调量越小，到达平衡状态时间越短。

3.5系统抖振分析

滑模控制本质上是一种不连续的开关控制，这种开关控制的特性使得系统在滑模面（也即平衡状态）上一定会有抖振发生。而图4中优化趋近律对应的红虚线曲线明显没有抖振产生。因此，将图4中优化趋近律对应的红虚线曲线与图6中优化趋近律对应的红虚线曲线比较，发现它们仅是系统仿真取样时间不同，其他并无区别，故而推断仿真时间的选取会影响到软件仿真步长，造成仿真一定程度上失真，从而导致系统无抖振的假象发生。故在进行系统仿真时，要选取合适的时间和步长。

综上可知，3种趋近律中，优化趋近律控制效果最好，参数ε和k的值对系统抖振均有影响。按照将系统抖振尽量削弱的原则，可以在取小值ε的同时，尽量取大k值，以减小系统到达平衡状态的时间，提高汽车EPS系统跟随性。优化趋近律在给出ε=diag［10，10］，k=diag［1000，1000］的情况下，比文献［4-6］、文献［8］、文献［10-11］的控制策略调整至平衡状态的时间分别快0.01，1.99，0.02，0.09，2.99，0.19s，且到达平衡状态过程中的动态品质更好。

4结论

文中给出了一种新型摇臂轴助力式EPS系统的状态方程，并将系统二级减速器累积磨损造成的角度间隙作为外界干扰，对此干扰进行正弦化处理。在采用特征向量任置法求出G矩阵后，通过对优化趋近律中ε和k的合理取值，可以保证系统快速到达平衡状态（跟随性好），同时又能减小超调量并有效削弱滑动模态切换引起的抖振。优化趋近律有效、可行，实现了对汽车转向快速跟随性的控制设计，验证了系统对外部扰动的不变性，为EPS转向系统提供了一种新的控制策略。此外，指数趋近律的形式仍可进一步优化，从而使系统获得更为优良的控制效果。

参考文献

［1］陈强，高天智，何宛芯，等.基于汽车电动助力转向系统的原理研究［J］.汽车实用技术，2021，46（16）：186-188.

［2］刘荣芬.新能源汽车锂电池及其技术发展探讨［J］.化工管理，2020，33（14）：94-95.

［3］李耀华，范吉康，何杰，等.考虑附着系数的商用车EPS控制策略［J］.重庆理工大学学报（自然科学），2021，35（12）：1-9.

［4］商显赫，林幕义，童亮，等.基于Dspace轻型货车EPS系统控制策略研究［J］.机械设计与制造，2022，60（2）：139-142.

［5］李洪强，孟建兵，曲宝军，等.基于粒子群算法的EPS系统控制策略（英文）［J］.机床与液压，2019，47（18）：39-44.

［6］商显赫，林幕义，陈勇，等.基于BP神经网络EPS系统控制策略研究［J］.机械设计与制造，2022，60（3）：36-40.

［7］王燮辉，李強，赵璐，等.C-EPS硬件在环仿真平台设计与控制策略验证［J］.浙江科技学院学报，2021，33（3）：239-247.

［8］孟令广，牛志刚.城市电动物流车EPS系统模糊PID控制策略研究［J］.机械设计与制造，2018，56（7）：33-36.

［9］汪洪波，夏志，胡振国.EPS多模式可拓模糊切换控制研究［J］.合肥工业大学学报（自然科学版），2018，41（8）：1084-1092.

［10］翁敬良，严运兵.基于操纵稳定性的EPS转向系统鲁棒控制策略研究［J］.武汉科技大学学报，2014，37（3）：204-209.

［11］赵万忠，施国标，林逸，等.循环球式EPS系统助力特性控制策略研究［J］.北京理工大学学报，2008，46（8）：702-705.

［12］晋兵营，聂建军，施国标.遗传算法优化的EPS系统模糊控制策略研究［J］.机械设计与制造，2010，48（5）：91-93.

［13］盛严，王超，陈建斌，等.结构滑模控制的一种指数趋近律方法［J］.噪声与振动控制，2002，22（4）：31-34.

［14］姚琼荟.变结构控制系统［M］.重庆：重庆大学出版社，1997.

［15］BRAHMIB，MOHAMEDHL，ABDELKRIMB，etal.Improvementofslidingmodecontrollerbyusinganewadaptivereachinglaw：Theoryandexperiment［J］.ISATransactions，2020，97：261-268.

［16］秦超，高锋阳，庄圣贤，等.基于一种指数趋近律的PMSM滑模变结构控制［J］.计算机仿真，2013，30（12）：306-310.

［17］张嗣瀛，高立群.现代控制理论，第2版［M］.北京：清华大学出版社，2017.

［18］ARNOLDL，SCHMALFUSSB.Lyapunovssecondmethodforrandomdynamicalsystems［J］.JournalofDifferentialEquations，2001，177（1）：235-265.