雷达桅杆振动有限元分析及减振设计
郭永亮 黄金林 丁 宁
(中远海运重工设计研究院 扬州 225200)
0 引 言
船舶上的雷达桅杆作为雷达等高精密电气设备的承载结构,良好的振动性能是船上电气设备正常运行的前提和保障。然而,由于雷达和信号灯等电气设备的功能要求,雷达桅杆需要布置在驾驶室正上方的罗经甲板上,桅杆主体与上层建筑直接相连,因此振动激励源的激振力可通过钢结构直接传导至雷达桅杆。此外,由于雷达桅杆特殊的结构形式(类似悬臂梁),其低阶模态频率往往较低,极易与上层建筑的低阶模态耦合,在船舶常用转速区间常与主机和螺旋桨等主要激励源产生共振问题。
考虑到雷达桅杆特殊的结构形式和复杂的舾装电气设备布置情况,若仅采用经验公式分析雷达桅杆的振动性能,其计算精度无法满足工程需要。目前,对于分析预报各种复杂的船舶振动问题,国内外很多学者和设计单位均采用三维空间有限元法,事实证明三维有限元模型是接近船舶真实结构的计算模型,能够较准确地计算船舶及其上结构的振动特性。[1-3]
本文采用有限元法对某散货船的雷达桅杆进行振动预报分析。在模态分析计算得到雷达桅杆低阶频率的基础上,计算雷达桅杆典型位置在主机、螺旋桨主要激励作用下的振动响应。在发现雷达桅杆存在振动风险后,提出结构修改方案以降低雷达桅杆的振动响应幅值,在详细设计阶段规避了雷达桅杆的振动风险。
1 概 述
1.1 船舶主要参数
该散货船主要参数见表1。

表1 某散货船主要参数
1.2 雷达桅杆布置情况及位置信息
本船雷达桅杆的布置情况及位置信息如图1 所示。

图1 某散货箱雷达桅杆的布置情况及位置信息
1.3 振动水平规范要求
本船规格书规定的船舶振动水平应该满足 ISO 6954: 2000(E)规范要求[4]。
2 确定振动激励源
对于普通商用船舶,主机和螺旋桨是引起船舶振动的主要激励源。主机产生的周期激振力主要可以分为2 种:一是运动部件惯性力产生的不平衡力和力矩;二是气缸内气体爆炸产生的对气缸侧壁的侧向压力和倾覆力矩,其对船体施加的激振力具体表现为各阶不平衡力和力矩、X 型振动激振力矩及H 型振动激振力矩[4]。螺旋桨作用于船舶的激振力频率等于桨轴转速乘以桨叶片数倍数的高阶激振力(又称为叶频激振力或倍叶频激振力),它是由螺旋桨在不均匀流场中工作引起的[5]。
本散货船基于主机设备资料及螺旋桨空泡实验,确定主机二阶不平衡力矩、三阶X 型激振力矩、六阶H 型激振力矩和螺旋桨脉动压力为主要振动激励源,在主机常用转速(normal continuous rating, NCR)下,振动主要激励源的激振力大小与频率如表2 所示。
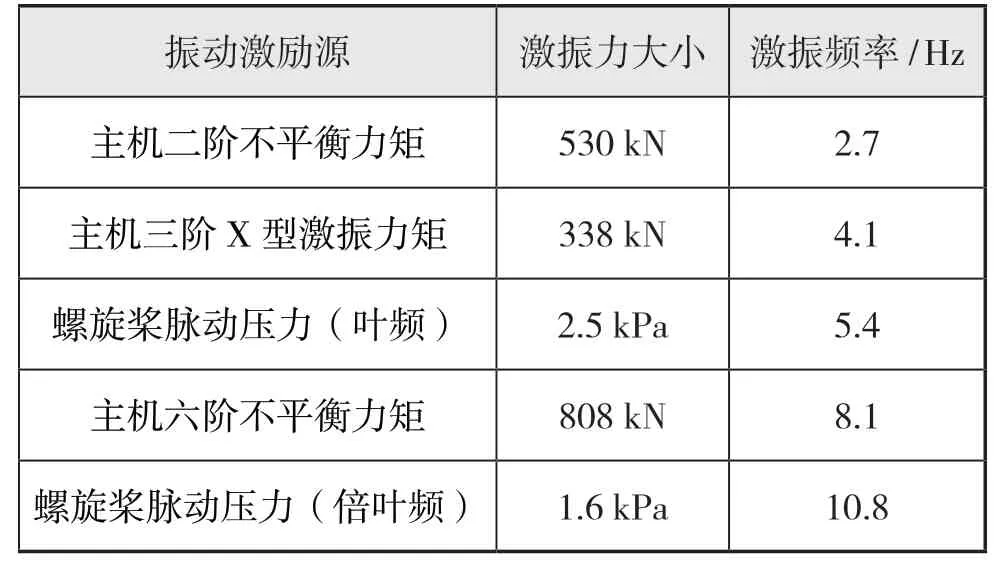
表2 NCR 下的主要激励源激振力大小与频率
3 建立有限元模型
本文运用MSC-Patran 有限元计算软件,基于总布置图、上层建筑结构图以及雷达桅杆布置图等图纸,在全船振动有限元模型的基础上,建立雷达桅杆有限元模型,对雷达桅杆进行独立的振动预报分析。
模型材料属性为钢制, 其密度为7 850 kg/m3, 杨氏模量为2.06×1011Pa,泊松比为0.3。坐标系定义:X轴,沿船舶纵向,自艉向艏为正;Y轴,沿船舶横向,左舷为正;Z轴,沿船舶垂向,向上为正。
雷达桅杆主体结构、2 层雷达平台及雷达平台对位加强等结构采用板单元(shell)建立;雷达支架及灯桅桁架结构采用梁单元(beam)建立;2 个波段雷达采用质量单元(mass)模拟;栏杆、扶手 、信号灯、喇叭和电缆等舾装电气件,采用定义板单元“Non-Structure”属性的形式,将其质量均匀分布到相应位置的板单元上。包含雷达桅杆的全船振动有限元模型如图2 所示。

图2 包含雷达桅杆的全船振动有限元模型
4 雷达桅杆模态分析
模态是结构的固有振动特性,包括固有频率、振型和阻尼比等。模态分析就是研究结构的这些模态参数,同时也是应用模态叠加法进行振动响应分析的基础。
本文以雷达桅杆为研究对象,对其进行模态分析。为减少全船其他位置的局部模态对雷达桅杆模态分析的干扰,选取上层建筑A 甲板以上包含雷达桅杆的有限元模型为研究对象,以A 甲板为边界条件设置固支约束,对雷达桅杆进行模态分析。
根据模态分析,得到2 个主要的雷达桅杆低阶模态,即:一阶纵向模态,模态频率5.1 Hz,如 图3 所示;一阶横向模态,模态频率5.3 Hz,如图4所示。

图3 雷达桅杆一阶纵向模态,频率5.1 Hz

图4 雷达桅杆一阶横向模态,频率5.3 Hz
通过模态分析可以发现,雷达桅杆的一阶横向模态和一阶纵向模态频率与螺旋桨叶频脉动压力频率接近,存在共振风险,因此有必要对其作进一步振动响应分析。
5 雷达桅杆振动响应分析
根据结构图纸准确建立的全船振动响应有限元模型,网格尺寸采用纵骨间距,以保证船体梁整体刚度和甲板板架、舱壁和雷达桅杆等局部结构刚度的准确模拟。全船质量、重心已根据空船质量统计表和装载手册进行调整。外板附连水通过定义 MFLUID 卡片的方式进行加载。模态阻尼的设定基于英国劳氏船级社的船舶振动指南[6],具体数值如表3 所示。

表3 频率响应分析中的模态阻尼
选取灯桅顶部及雷达桅杆上平台中心位置为振动响应分析的典型位置,如图5 所示。
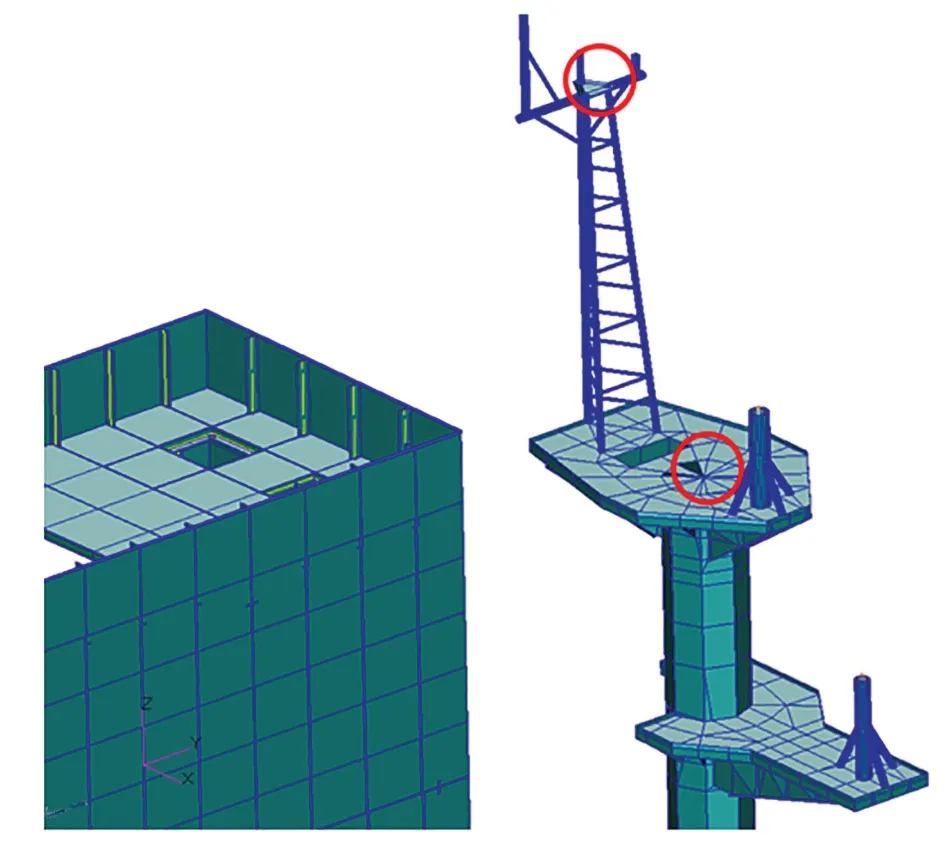
图5 雷达桅杆振动响应分析典型位置
以本文表1 中选定的主要激励源为外部载荷,进行全船振动响应分析。经全船振动响应分析发现,当主机转速达到77 r/min 附近,螺旋桨叶频脉动压力频率为5.1 Hz 时,此时雷达桅杆与螺旋桨叶频脉动压力发生共振,振动响应急剧放大,这与雷达桅杆模态分析的结果相吻合。
雷达桅杆选取的2 处典型位置在螺旋桨叶频脉动压力作用下的纵向振动响应曲线如下页图6 所示。雷达桅杆上平台振动响应峰值为48 mm/s,灯桅顶部振动响应峰值更是达到了266 mm/s,该振动响应结果是不可接受的,必须寻求方案进行减振设计,以降低雷达桅杆的振动响应。
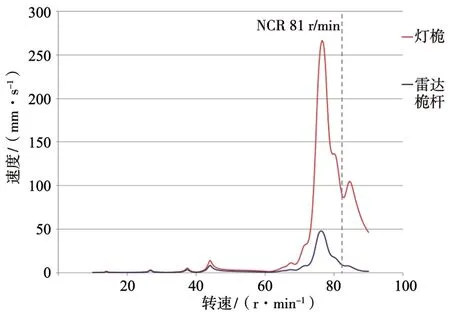
图6 典型位置雷达桅杆纵向振动响应曲线
6 减振设计
6.1 降低雷达平台高度
由于雷达桅杆类似于悬臂梁的特殊结构形式,降低雷达平台高度可以显著降低其振动响应。经与舾装、电气专业沟通,在保证不影响雷达功能的前提下,雷达平台高度最多可降低500 mm。
降低雷达平台减振方案示意及选取的2 处典型位置在螺旋桨叶频脉动压力作用下的纵向振动响应曲线如图7 所示。
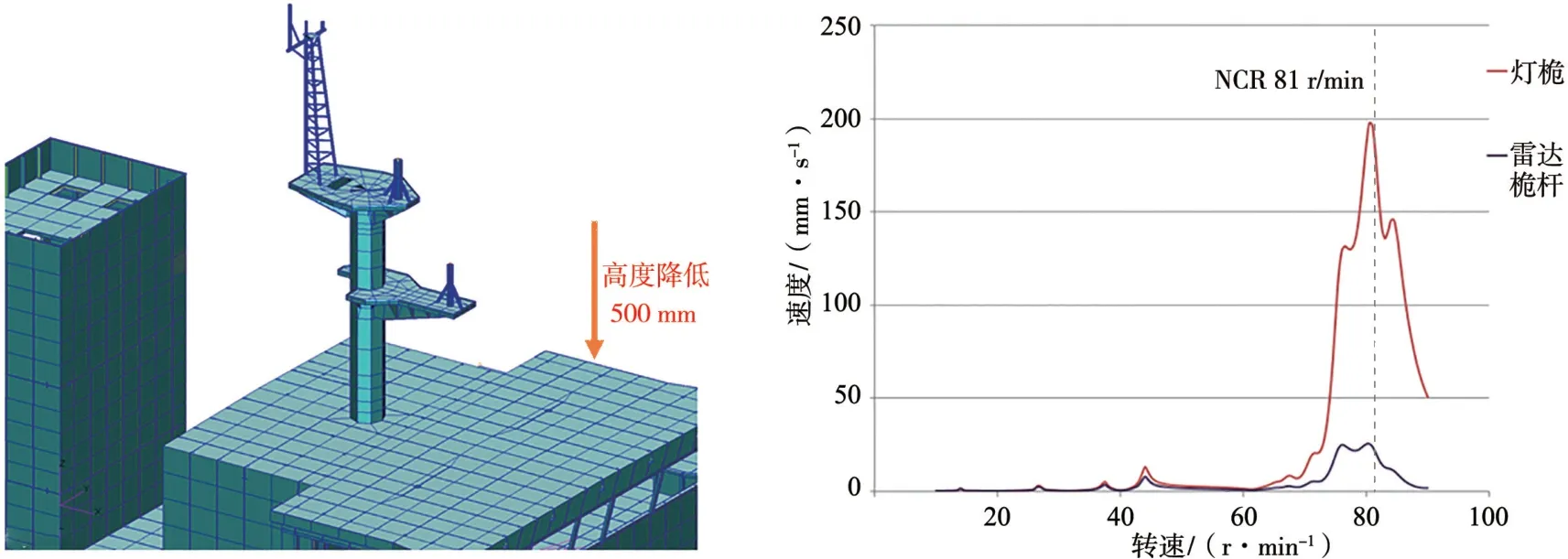
图7 降低平台高度方案及典型位置雷达桅杆纵向振动响应曲线
由计算结果可知:降低平台高度后,典型位置的振动响应峰值有所降低,其中雷达桅杆上平台振动响应峰值为25 mm/s,可以接受;灯桅顶部振动响应峰值为197 mm/s,仍然处于较高振动水平。同时,由于雷达桅杆长度变短,整体刚度略有提升,一阶纵向固有频率由5.1 Hz 提升至5.3 Hz,振动响应峰值前移到主机转速80.5 r/min 附近,与主机常用转速81 r/min 十分接近,不可接受。
6.2 灯桅斜撑结构加强
在降低雷达桅杆平台高度方案的基础上,在灯桅上增加斜撑加强以增加灯桅的刚度,提升灯桅的固有频率。灯桅斜撑加强减振方案示意及选取的2处典型位置在螺旋桨叶频脉动压力作用下的纵向振动响应曲线如图8 所示。
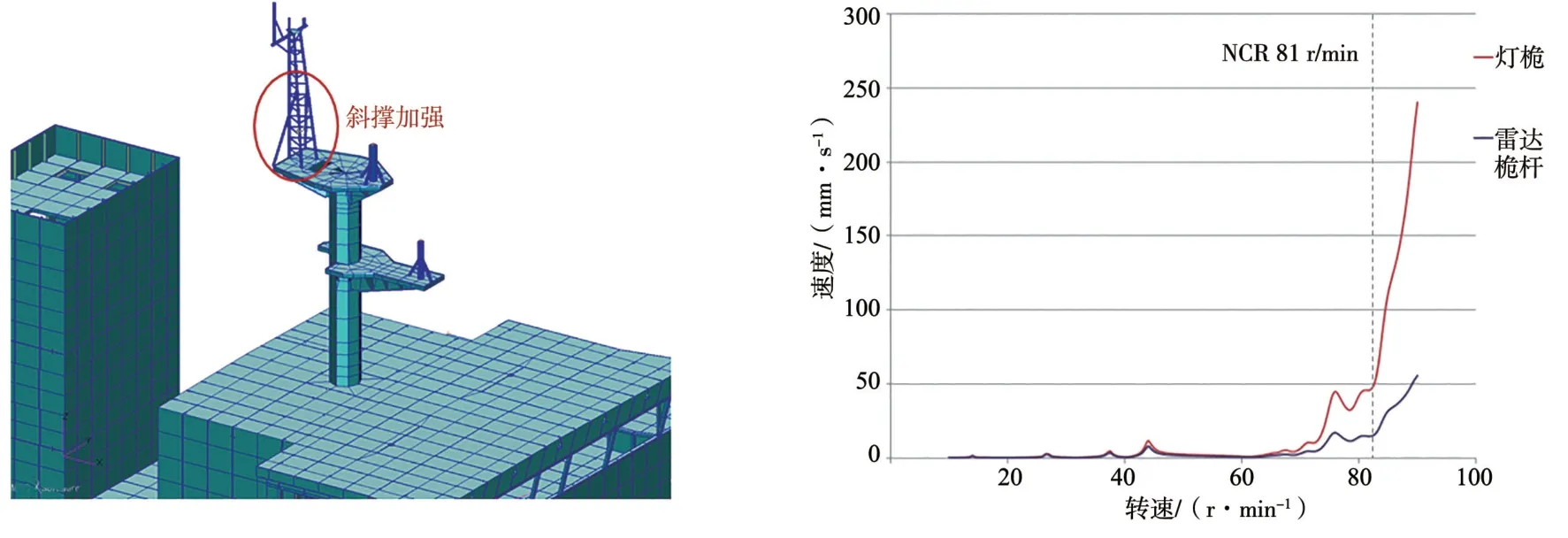
图8 灯桅斜撑结构加强方案及典型位置雷达桅杆纵向振动响应曲线
增加斜撑加强后,灯桅的刚度提升,但与螺旋桨脉动压力的共振峰被推移至90 r/min 以后,灯桅在83 r/min 后的振动响应幅值仍会急剧增加,在主机最大持续转速(specified maximum continuous rating, SMCR)88 r/min 下,灯桅典型位置处的纵向振动响应为168 mm/s,仍存在振动风险。
6.3 增加配重块
在降低雷达桅杆平台高度方案的基础上,在灯桅顶部增加100 kg 配重块以增加灯桅的质量,降低灯桅的固有频率。灯桅顶部增加配重块减振方案示意及选取的2 处典型位置在螺旋桨叶频脉动压力作用下的纵向振动响应曲线如图9 所示。
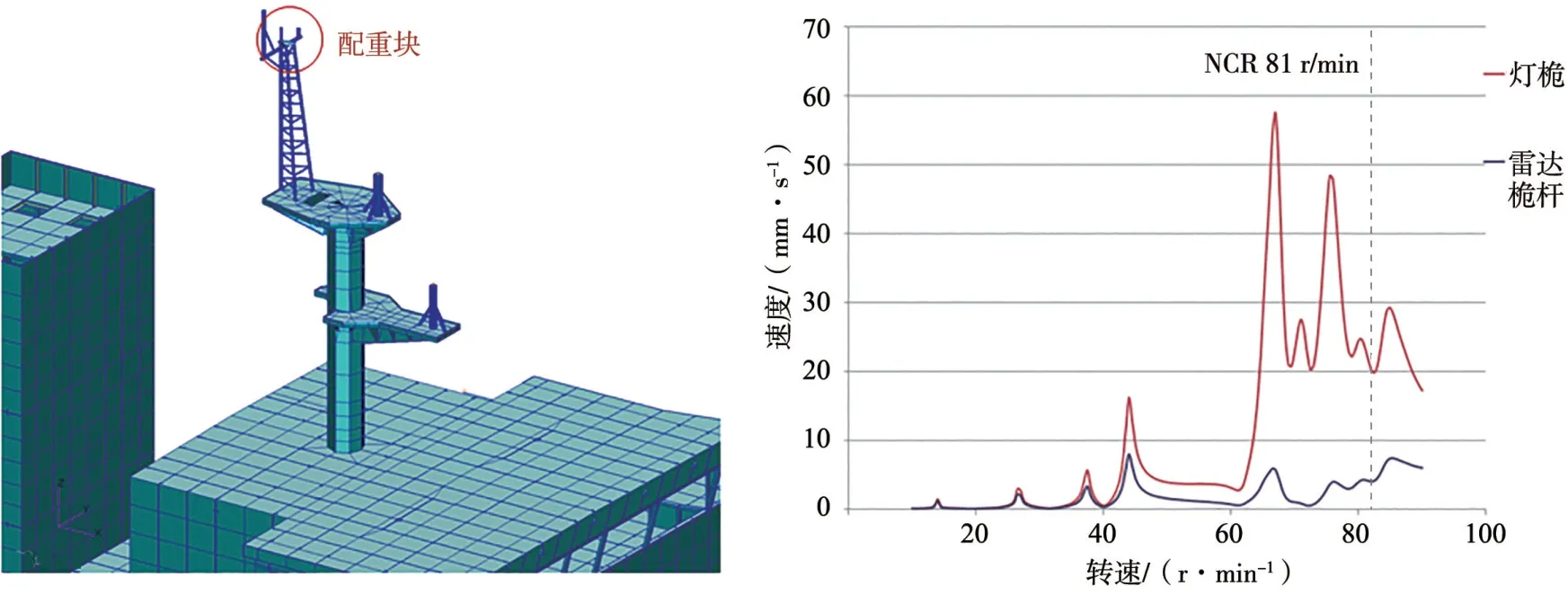
图9 灯桅增加配重块方案及典型位置雷达桅杆纵向振动响应曲线
增加配重块后,灯桅的固有频率降低,最大峰值位置被推移至主机转速67 r/min,振动响应降低至57 mm/s。峰值降低至可接受水平且出现的主机转速远离NCR,减振效果理想,故该方案被选定为最终的减振方案。
7 结 语
本文通过对某散货船的雷达桅杆进行有限元建模、模态分析和振动响应分析,发现其与螺旋桨脉动压力存在共振风险。在与舾装、电气等相关专业沟通后,分别提出了降低雷达桅杆平台高度、斜撑结构加强及增加配重块等减振方案。通过对比分析不同减振方案的振动响应计算结果,最终确定了降低雷达平台500 mm 并同时增加灯桅100 kg 配重块的雷达桅杆减振设计组合方案,在详细设计阶段规避了本船雷达桅杆的振动风险。

