从常识走向数学,突出数学化过程
范林伟


弗赖登塔尔认为,数学化可以分为横向数学化和纵向数学化。前者强调把生活世界引向符号世界,后者强调将数学知识进行关联乃至引向深入。学生学习数学的过程就是他们在生活中发现数学,再到认识数学知识之间联系与区别的过程。《义务教育数学课程标准(2022年版)》在第三学段“图形的认识与测量”的教学提示中指出,要使学生经历根据“两点间线段最短”的基本事实说明三角形三边关系的过程,形成推理意识。那么,这节课又将如何数学化地实施呢?下面笔者以朱国荣老师的课堂实例为例,与大家共同感受名师智慧。
一、源于生活常识,认识基本事实
师:同学们,看看黑板,猜猜这是什么?如图1,这里有一条直线,它代表一条小河,用字母l表示。A、B这两个点代表的是两个村庄。
师:今天,朱老师要请大家做一个设计师。这两个村庄,从A村到B村,或者,从B村到A村都要经过这条小河。但是,现在这条小河上面还没有桥。我们要在这条河的上面架一座桥。请同学们思考一下,在哪里架桥从A村到B村的距离最短呢?
(学生上台演示,连接A、B两点,标出与直线l的交点)
师:只要把A点和B点连起来,在这个交点上架桥,两个村庄之间的距离就是最短的了。你们同意吗?
生(齐):同意!
师:老师有个疑问,难道我在这儿(直线上的其他点)架桥路程就不是最短吗,为什么呀?
生:因为如果在这里架桥,就跟跑步比赛一样。你走弯路肯定跑得要更远,所以距离就更长。
师(补画出三角形):如果你拐个弯儿,那么这两条线段加起来就会比这条线段要长。这就是我们发现的一个结论:两点之间怎么样最短?
生:两点之间直线段最短。
师:看来我们都是合格的小设计师!当然,这个道理其实一年级的学生也知道。如图2,小明要去上学,他家到学校有三条路可走,如果他没有特殊情况,他会走哪一条?
生:他肯定走第②条,因为第②条是直线。
师:这个道理不仅一年级学生知道,小狗也知道,你相信吗?
生(观察图3):小狗肯定也会直着跑过去,弯过去太麻烦了。
师:是的,这样的道理不仅设计师知道,一年级学生知道,小狗也知道。这样的道理我们给它一个名称——基本事实。
【赏析】基本事实是人们在长期大量的生活常识中总结出来的一般化的经验,是一种普遍的共识,具有可感知性、真实性、基础性等特点。教学中,朱老师以架桥为话题,以小设计师为引子调动学生的学习积极性,从现实问题中抽象出三角形,然后引导学生根据生活常识来判断与思考,接着以“小明上学不走弯路”和“小狗也知道要走直线”两个例子生动形象地揭示出这些现象中蕴含的基本事实,使学生从常识中发现数学,自然地实现了横向数学化。
二、根据基本事实发现数学规律
师:我们知道了这个基本事实有什么用吗?今天,我们要借助这个基本事实来研究三角形的特点,我们要研究三角形三条边长之间的关系。
师(出示一张白纸):请大家先在这张白纸上任意画一个三角形,然后把这三条边的长度分别用三个字母a、b、c来表示。
(学生画三角形,标记边的名称)
师:下面,我们要开始像数学家一样研究了。请你们联系“两点之间直线段最短”这一基本事实,研究三条边长度之间的关系。静静地想一想:你们能找到什么规律呢?
(学生四人小组讨论,交流想法)
生:我的三角形中,a、b、c中有一条边是最长的,有一条边是最短的。
生:我的三角形有两条边是一样长的。
师:并不是所有的三角形都是这样的,能不能说是一个规律?
生:三角形中有一条边是最长的,有一条边是最短的,还有一条边就是中间长的。中间长的和最短的加起来肯定比最长的要长。
师:你们同意吗?
生:同意。
生:不同意,我没有最长和最短的。我的三角形三条边都是一样长的。
师:a加b和c比会怎么样?
生:a+b>c。
师:你怎么知道一定是大于呢?
生:那个基本事实就说两点之间直线段最短。那么,c就是直线段,a加b就不是直线段的,所以会更长,也就是a加b比c要长。
师:老师也任意画一个三角形,然后任意把这三边条标为a、b、c。请问a+b长,还是c长?
生:a+b。
师:你不量,怎么就知道了呢?
生:因为两点之间直线段是最短的,a加b已经拐弯了,所以a+b>c。
师:看一眼你们的纸上,a+b大于c吗?
生(齐):大于。
(同桌交流,再说理由)
师:同学们,刚才我们已经研究出来 a加b大于c,谁还能再说一个这样的式子?
生:a+c>b。
生:b+c>a。
师:你们研究得非常好!同学们,通过刚才的研究,大家发现了不管什么样的三角形,三条边的长度之间有什么关系?
生:三角形的一条边加另一条边一定比剩下的一条边长。
(板书:任意两边之和大于第三边)
【赏析】教学中,朱国荣老师组织学生从自己创造的任意三角形中发现三角形三条边的关系。期间,朱老师充分暴露学生的思考与发现,使他们感悟到“并不是所有的三角形都有这样的特点”,进而运用数学事实来进行推理与分析,巧妙引导学生从不同的特征中寻找共同的规律。也正是这些不同声音使学生不断地去思考、去联系基本事实来进行推理,进而更好地促进他们聚焦数学规律的本质。于是,学生在辨析与判断中深刻地体验了数学规律的普適性,感受到基于数学事实进行数学推理的简洁性与准确性,逐步从横向数学化走向纵向数学化,经历了基本的数学推理过程。
三、应用规律解决具体问题
师:刚才,我们根据这个基本事实得到了一个规律。现在,我们对三角形的研究有了初步的结论和发现。同学们,你们发现这个规律有什么用吗?
生:以后走路就走直线最近,可以最快到达目的地。
生:如果走三角形的路,就不要走转弯的路,要走笔直的那条路。
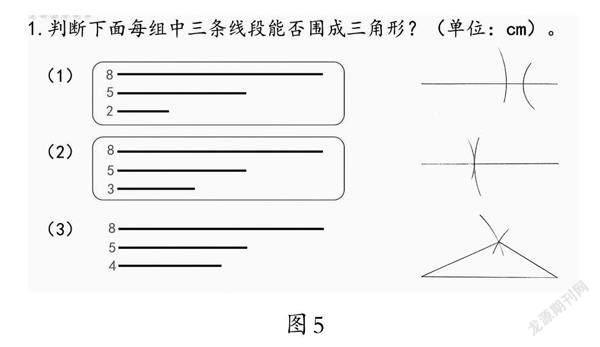
师:在数学中,它还有什么用呢?我们来判断图4每组中三条线段能否围成三角形?
(教师逐一呈现,学生独立思考)
师:想一想,哪一组能围成三角形?哪一组不能,为什么?
(四人小组讨论,教师倾听)
生:因为8厘米那么长,如果2厘米在上面,5厘米在旁边,8厘米在下面的话,肯定要超过了好多。
师:他想表达的意思是,8厘米、5厘米、2厘米,他认为能还是不能?
生:不能。
师:有没有认为能的?
生:我觉得可以,因为如果我把这个8厘米和5厘米加在一起就是13厘米,那么13>2。(板书:8+5>2)
师:是的,我们还可以找到8+2>5。我们能找到两组了,为什么还是不能呢?(板书:8+2>5)
生:因为8厘米是最长的那条边,剩下的两条边之和等于7厘米,怎么也不会拼在一起啊!(板书:5+2<8)
师:现在是一个小于,两个大于,你们觉得能不能围成三角形,为什么?
生:任意两条边的意思就是这三个都要符合。
师:看来第一组的确不能围成三角形。我们接着再看第二组,它们可不可以呢?
生:5加3等于8,所以也不可以。
师:他说有一种相等了,他认为就不可以。你们同意吗?你们觉得其他两个算式还要不要写?
生:不要,因为已经不符合要求了。
师:最后一个呢?
生:可以。因为8+5>4,4+5>8, 4+8>5。
师:他报了三个算式,你们都同意他这样的方法吗?那如果要说它能,朱老师该写三个算式还是写一个算式呢?
生:三个。
师:你们觉得判断的时候我该写三个算式还是可以少写一点?
生:我觉得可以写一个算式,只要把最小的两个加起来和最长的比一比就行了。
师:4+5>8,后面两个为什么就不要写了呢?
生:最大的加任意一个小的肯定比另外一个大了,所以不用写。
师:也就是说,我们在判断的时候,只要把较短的两条边加起来就可以了,对吗?
生:对!
师:经过刚才的研究,我们发现:在判断的时候,不用把另外两条边之和加起来,只要加最短的两条边便可。如果最短的两条边之和都能大于另外一条边,那么就可以了。因此,在判断的时候,我们只要根据“较短两边之和大于第三边”就可以了。
【赏析】数学学习不仅要学习概念、性质、法则和定理等,更要学习数学知识之间的关联,以及如何运用数学知识去解决现实中的数学问题。于是,朱老师以问题链的形式将学生的思维引向深入。通过“这个规律有什么用吗?”“每组中三条线段能否围成三角形?”两个问题组织学生交流、辨析,让学生在利用规律解决数学问题的过程中进一步理解三角形三边关系的具体含义,体会其数学价值。并且,朱老师还巧妙地利用课堂生成及时沟通了规律运用与数学判断之间的联系与区别,使学生充分体会“较短两边之和大于第三边”的优势。整个过程,学生学得灵活机动、有的放矢,教师顺学而导、精益求精。
四、適度拓展发展几何直观
师:有三条线段分别为8厘米、5厘米和4厘米,如果把这三条线段围成三角形的话,这个三角形会是什么样?你们能不能把这样的一个三角形准确地画出来?请大家在纸上找个空白的地方试试看。
(学生尝试用直尺画三角形)
师:你们觉得,我拿把尺子就能把这个三角形画出来,容易吗?你们碰到什么困难了?
生:我们把第二条边画好之后,最后的一条边不一定是我们原来要得到的那条边。
师:你们听懂了吗?我们来假设一下:我先画了一条8厘米的线段,这条很容易。我再画一条5厘米的线段,也很容易。但是,此时我们遇到什么困难了?
生:最后一条画出来可能会大于也可能小于4厘米,一下子凑不准了。
师:有这个困惑的同学请举手?(大多数学生举手)你们觉得怎样解决这个问题呢?有没有办法能够比较准确、方便地画出这个三角形呢?
生:如果第三条边不行,就把第二条边的那个角度换一下再画一次。
师:是的,只要坚持下去总会被你们试到的。还有什么办法吗?(学生沉默)同学们,你们知道吗?现在只有这把尺子可不行,还要有一个新工具来帮助我们!今天我们还带了什么工具?(圆规)对呀!同学们如果借助这个圆规,只要掌握了方法,你们就能把这个三角形画出来!
(教师引入微课,学生观看学习,再尝试画三角形)
师:画出来了吗?祝贺同学们都画成功了!把圆规先放一放,我们继续看屏幕。刚才我们用圆规就找到了这个三角形的顶点,这个点到这个顶点的距离是5厘米,到另一个顶点的距离正好是4厘米,这就是圆规的作用!
师:刚才你们还说前两组也是不行的,如果我们也用圆规来试一试的话,会碰上什么问题呢?请大家选一个,然后在白纸的背面试试看。
(学生尝试画三角形)
师:我们交流一下,为什么8厘米、5厘米和2厘米的线段不行?
生:画下来,这个上面交叉点没有了。
师:是的,两条弧画好之后,不能找到交叉点。那8厘米、5厘米和3厘米的线段,为什么不行?
生:8厘米、5厘米和3厘米的线段有交叉点,就是交叉点直接在横线上了。
师:对,交叉点是有的,但是直接交叉在那条8厘米的线段上了。
(教师呈现结果,学生见证结果,如图5)
师:同学们,回想一下,在今天这节课上学了哪些知识?
生:我学到了基本事实:两点之间直线最短 。
生:我们还发现了一个规律:三角形任意两边之和大于第三边。
师:这个规律我们是通过什么办法得到的?
生:我们先随便画一个三角形,然后结合这个基本事实得出那两条边大于第三边。
生:我还学到了较短两边之和大于第三边。
师:我们在做判断的时候要不要把这三个算式都写出来?(不要)是的,只要用较短两边之和与第三边比较就可以了。
生:我还学会了用圆规画三角形。
师:是啊,当三角形的三条边指定的时候,我们用直尺很难画三角形。这个时候我们可以借助圆规来画。
【赏析】最后,朱老师巧妙地借助习题过渡到画三角形,然后运用微课使学生体会用“尺规”作三角形的神奇之处。同时,他又以“画三角形”为任务驱动学生借助直尺与圆规再探究前两个三角形为什么围不成的原因,让学生进一步感受尺规作图的数学价值。并且,“画三角形”的过程,学生经历了一种新的解决问题方式——几何直观,从而破除了学生“思而不得、想而不见”的思维困局,实现了从空间想象到见证现实的跨越。
整节课,朱老师将生活问题抽象成数学问题,成功地将学生帶入了数学世界,使学生感受数学与生活之间的紧密联系,这体现了横向数学化的特征;然后,他智慧地引导学生从基本事实出发,组织学生全面经历观察、分析、推理与运用的过程,使学生利用基本事实探究发现三角形的三边关系,并运用这一基本规律判断与解决实际问题,感受数学推理的应用价值,这一步步深入的过程就体现了纵向数学化的特征。
无论是根据“两点间直线段最短”发现三角形三边关系,还是利用三边关系判断三条线段能否围成三角形,或者是利用尺规来画三角形,这些活动都有效地发展了学生的推理意识和动手操作能力,增强了他们的几何直观意识,使得学生在讲道理的过程中掌握了数学推理与表达的一般方式,养成了全面思考问题的好习惯。同时,“画三角形”这一活动更有意识地融入了尺规作图的思维方式,使学生初步感受到此方法的数学魅力与验证价值。
(作者单位:浙江师范大学附属嘉善实验学校)

