概率与数列、导数、函数和方程等知识交汇的创新题型

■河南省固始县信合外国语高级中学 胡云兵

2019年高考全国Ⅰ卷首次把概率题作为压轴题出现,当时引起一片哗然,这是在传递什么信号? 概率统计题何去何从? 我们要如何备考? 带着这些问题,我们从近几年全国卷和部分省份的概率高考题,发现概率题增加难度,不是概率知识本身增加难度,而是难在概率与其他数学知识交汇处命题。下面通过几道高考题来说明概率与其他数学知识交汇的创新题型。

一、概率与数列的交汇

例1(2019 全国Ⅰ卷理数第21 题)为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验。试验方案如下:每一轮选取两只白鼠对药效进行对比试验。对于两只白鼠,随机选一只施以甲药,另一只施以乙药。一轮的治疗结果得出后,再安排下一轮试验。当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效。为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈,则甲药得1 分,乙药得-1 分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈,则乙药得1 分,甲药得-1 分;若都治愈或都未治愈,则两种药均得0分。甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X。

(1)求X的分布列。

(2)若甲药、乙药在试验开始时都赋予4分,pi(i=0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=-1),b=P(X=0),c=P(X=1)。假设α=0.5,β=0.8。

(i)证明:{pi+1-pi}(i=0,1,2,…,7)为等比数列;

(ii)求p4,并根据p4的值解释这种试验方案的合理性。

解析：(1)X的所有可能取值为-1,0,1。

P(X=-1)=(1-α)β,P(X=0)=αβ+(1-α)(1-β),P(X=1)=α(1-β)。

故X的分布列如表1。

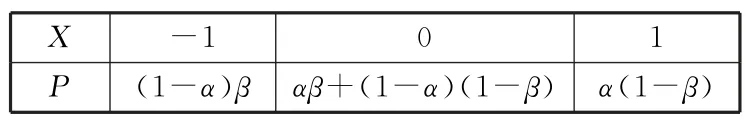
表1

(2)(i)已知α=0.5,β=0.8,故由(1)得,a=0.4,b=0.5,c=0.1。

因此,pi=0.4pi-1+0.5pi+0.1pi+1(i=1,2,…,7)。

整理得0.1(pi+1-pi)=0.4(pi-pi-1),即pi+1-pi=4(pi-pi-1)。

又p1-p0=p1≠0,故{pi+1-pi}(i=0,1,2,…,7)为公比为4,首项为p1的等比数列。

(ii)由(i)可得:

p4表示最终认为甲药更有效的概率。

由计算结果可以看出,在甲药治愈率为0.5,乙药治愈率为0.8时,认为甲药更有效的概率为,此时得出错误结论的概率非常小,说明这种试验方案合理。

点评:本题是函数与数列的综合题,主要考查数列和函数的应用,考查离散型随机变量的分布列。根据条件推出数列的递推关系是解决本题的关键。其本质仍然是常规的概率与统计问题,只是其中涉及了数列问题的应用,一般转化为等差、等比数列的定义、通项公式或者数列求和问题。

二、概率与函数、方程和导数的交汇

例2(2021新高考Ⅱ卷第21 题) 一种微生物群体可以经过自身繁殖不断生存下来,设一个这种微生物为第0代,经过一次繁殖后为第1 代,再经过一次繁殖后为第2代,……,该微生物每代繁殖的个数是相互独立的且有相同的分布列,设X表示1个微生物个体繁殖下一代的个数,P(X=i)=pi(i=0,1,2,3)。

(1)已知p0=0.4,p1=0.3,p2=0.2,p3=0.1,求E(X)。

(2)设p表示该种微生物经过多代繁殖后临近灭绝的概率,p是关于x的方程:p0+p1x+p2x2+p3x3=x的一个最小正实根。求证:当E(X)≤1 时,p=1;当E(X)＞1时,p＜1。

(3)根据你的理解,请说明(2)问结论的实际含义。

解析：(1)E(X)=0×0.4+1×0.3+2×0.2+3×0.1=1。

(2)设f(x)=p3x3+p2x2+(p1-1)x+p0。

因为p3+p2+p1+p0=1,所以f(x)=p3x3+p2x2-(p2+p0+p3)x+p0。

①若E(X)≤1,则p1+2p2+3p3≤1,故p2+2p3≤p0。

f'(x)=3p3x2+2p2x-(p2+p0+p3)。

因为f'(0)=-(p2+p0+p3)＜0,f'(1)=p2+2p3-p0≤0,所以f'(x)有两个不同零点x1,x2,且x1＜0＜1≤x2。

当x∈(-∞,x1)∪(x2,+∞)时,f'(x)＞0;当x∈(x1,x2)时,f'(x)＜0。

故f(x)在(-∞,x1)上为增函数,在(x1,x2)上为减函数,在(x2,+∞)上为增函数。

若x2=1,f(x)在(x2,+∞)为增函数且f(1)=0。而当x∈(0,x2)时,因为f(x)在(x1,x2)上为减函数,所以f(x)＞f(x2)=f(1)=0,故1为p0+p1x+p2x2+p3x3=x的一个最小正实根。

若x2＞1,因为f(1)=0 且在(0,x2)上为减函数,所以1为p0+p1x+p2x2+p3x3=x的一个最小正实根。

综上,若E(X)≤1,则p=1。

②若E(X)＞1,则p1+2p2+3p3＞1,故p2+2p3＞p0。

此时f'(0)=-(p2+p0+p3)＜0,f'(1)=p2+2p3-p0＞0,故f'(x)有两个不同零点x3,x4,且x3＜0＜x4＜1。

当x∈(-∞,x3)∪(x4,+∞)时,f'(x)＞0;当x∈(x3,x4)时,f'(x)＜0。

故f(x)在(-∞,x3)上为增函数,在(x3,x4)上为减函数,在(x4,+∞)上为增函数。

而f(1)=0,故f(x4)＜0。

又f(0)=p0＞0,故f(x)在(0,x4)存在一个零点p,且p＜1。

所以p为p0+p1x+p2x2+p3x3=x的一个最小正实根,此时p＜1。

故当E(X)＞1时,p＜1。

(3)结论的实际含义:每一个该种微生物繁殖后代的平均数不超过1,则若干代必然灭绝;若繁殖后代的平均数超过1,则若干代后被灭绝的概率小于1。

点评:在概率与统计的问题中,决策的工具是样本的数字特征或有关概率。决策方案的最佳选择是将概率最大(最小)或均值最大(最小)的方案作为最佳方案,这往往借助于函数、不等式或数列的有关性质去实现。

例3(2018 年全国Ⅰ卷理数第20题)某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品进行检验,如检验出不合格品,则更换为合格品。检验时,先从这箱产品中任取20件进行检验,再根据检验结果决定是否对余下的所有产品检验。设每件产品为不合格品的概率都为p(0＜p＜1),且各件产品是否为不合格品相互独立。

(1)记20件产品中恰有2件不合格品的概率为f(p),求f(p)的最大值点p0。

(2)现对一箱产品检验了20 件,结果恰有2件不合格品,以(1)中确定的p0作为p的值。已知每件产品的检验费用为2 元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用。

①若不对该箱余下的产品进行检验,这一箱产品的检验费用与赔偿费用的和记为X,求E(X);

②以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验?

令f'(p)=0,得p=0.1。

当p∈(0,0.1)时,f'(p)＞0;

当p∈(0.1,1)时,f'(p)＜0。

所以f(p)的最大值点为p0=0.1。

(2)由(1)知,p=0.1。

①令Y表示余下的180件产品中的不合格品件数,依题意知Y～B(180,0.1),X=20×2+25Y,即X=40+25Y。

所以E(X)=E(40+25Y)=40+25E(Y)=40+25×180×0.1=490。

②若对余下的产品作检验,则这一箱产品所需要的检验费用为400元。

由于E(X)＞400,故应该对余下的产品作检验。

点评:解决概率和函数、导数的综合问题,关键是读懂题意,将与概率有关的问题(尤其是最值问题)转化为函数问题,再利用函数或导数知识解决,在转化过程中,对已知条件进行适当变形、整理,使之与求解的结论建立联系,从而解决问题。

三、概率与不等式的交汇

例4(2017 年江苏卷第23 题)已知一个口袋有m个白球,n个黑球(m,n∈N*,n≥2),这些球除颜色外完全相同。现将口袋中的球随机地逐个取出,并放入如表2 所示的编号为1,2,3,…,m+n的抽屉内,其中第k次取球放入编号为k的抽屉(k=1,2,3,…,m+n)。

表2

(1)试求编号为2 的抽屉内放的是黑球的概率p;

(2)随机变量X表示最后一个取出的黑球所在抽屉编号的倒数,E(X)是X的数学期望,证明

解析：(1)编号为2的抽屉内放的是黑球的概率

(2)随机变量X的概率分布如表3。

表3

随机变量X的期望为:

点评:本题表面看起来是概率问题,但是它重点恰在不等式,所以对于概率统计问题,我们要有意关注与其他数学知识的整合。同时也提醒我们要跳出固定思维模式,学会灵活处理问题的能力。