正态分布导学

■河北省秦皇岛市北戴河中学 陈 芳

一、知识要点梳理

1.正态曲线。

正态曲线沿着x轴方向水平移动只能改变对称轴的位置,曲线的形状没有改变,所得的曲线依然是正态曲线。显然对于任意x∈R,f(x)＞0,它的图像在x轴的上方。可以证明x轴和曲线之间的区域的面积为1。我们称f(x)为正态密度函数,称它的图像为正态分布密度曲线,简称正态曲线。若随机变量X的概率密度函数为f(x),则称随机变量X服从正态分布,记为X～N(μ,σ2)。特别地,当μ=0,σ=1时,称随机变量X服从标准正态分布。

2.由X的密度函数及图像可以发现,正态曲线还有以下特点。

(1)曲线是单峰的,它关于直线x=μ对称;(2)曲线在x=μ处达到峰值当|x|无限增大时,曲线无限接近x轴。

3.正态分布的期望与方差。

若X～N(μ,σ2),则E(X)=μ,D(X)=σ2。

4.正态变量在三个特殊区间内取值的概率。

(1)P(μ-σ≤X≤μ+σ)≈0.682 7;

(2)P(μ-2σ≤X≤μ+2σ)≈0.954 5;

(3)P(μ-3σ≤X≤μ+3σ)≈0.997 3。

在实际应用中,通常认为服从于正态分布N(μ,σ2)的随机变量X只取[μ-3σ,μ+3σ]中的值,这在统计学中称为3σ原则。

二、典型例题解析

题型一：正态曲线图像的应用

例1设有一正态总体,它的概率密度曲线是函数f(x)的图像,且,则这个正态总体的平均数与标准差分别是( )。

A.10与8 B.10与2

C.8与10 D.2与10

解析：(1)因为,所以σ=2,μ=10,即正态总体的平均数与标准差分别为10与2。

选B。

题型二：利用正态分布的对称性求概率

例2正态分布概念是由德国数学家和天文学家Moivre在1733 年首次提出的,由于德国数学家高斯率先把其应用于天文学研究,故我们把正态分布又称作高斯分布。早期的天文学家通过长期对某一天体的观测收集到大量数据,对这些数据进行分析,发现这些数据变量X近似服从N(9,σ2)。若P(X＜10)=0.91,则P(X≤8)=_____。

解析：因为X近似服从N(9,σ2),所以X的正态分布曲线关于x=9 对称,故P(X≤8)=P(X≥10)=1-P(X＜10)=1-0.91=0.09。

题型三：正态分布的实际应用

例3学史明理,学史增信,学史崇德,学史力行。近年来,某市积极组织开展党史学习教育的活动,为调查活动开展的效果,市委宣传部对全市多个基层支部的党员进行了测试,并从中抽取了1 000份试卷进行调查,根据这1 000 份试卷的成绩(单位:分,满分100分)得到如下频数分布表(表1)。

表1

(1)求这1 000份试卷成绩的平均数。(同一组中的数据用该组区间的中点值为代表)

(2)假设此次测试的成绩X服从正态分布N(μ,σ2),其中μ近似为样本平均数,σ2近似为样本方差s2,已知s的近似值为6.61,以样本估计总体,假设有84.14%的党员的测试成绩高于市委宣传部预期的平均成绩,则市委宣传部预期的平均成绩大约为多少?(结果保留一位小数)

(3)市委宣传部准备从成绩在[90,100]内的120份试卷中用分层抽样的方法抽取6份,再从这6份试卷中随机抽取3份进一步进行分析,记Y为抽取的3份试卷中测试成绩在[95,100]内的份数,求Y的分布列和数学期望。

解析：(1)设这1 000份试卷成绩的平均数为,则:

(2)由(1)得μ=82.15,且σ=6.61。

Y的分布列如表2。

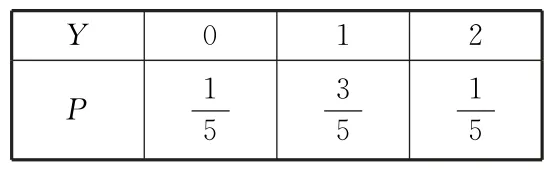
表2

题型四：标准正态分布

例42021年某地在全国志愿服务信息系统注册登记志愿者8 万多人,2020年7 月份以来,共完成1 931个志愿服务项目,8 900多名志愿者开展志愿服务活动累计超过150 万小时。为了了解此地志愿者对志愿服务的认知和参与度,随机调查了500 名志愿者每月的志愿服务时长(单位:小时),并绘制如图1所示的频率分布直方图。

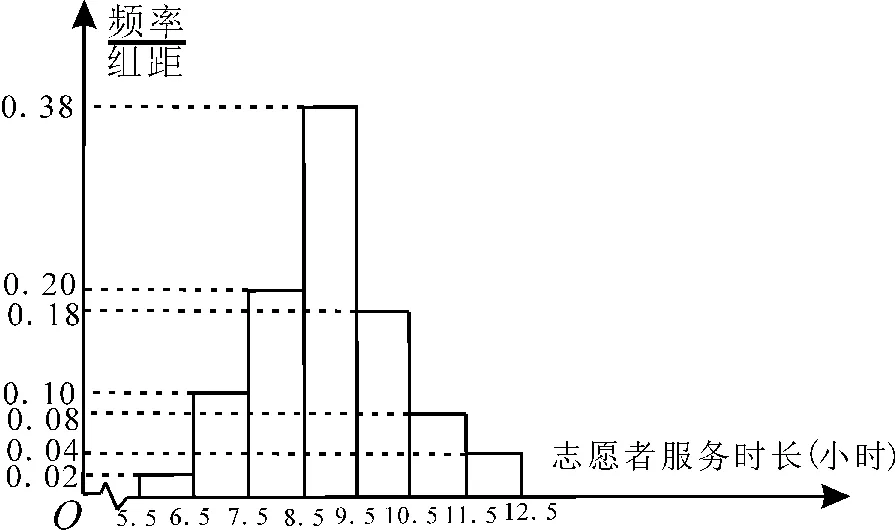
图1

(1)估计这500 名志愿者每月志愿服务时长的样本平均数和样本方差s2(同一组中的数据用该组数据区间的中间值代表)。

(i)利用直方图得到的正态分布,求P(X≤10);

(ii)从该地随机抽取20 名志愿者,记Z表示这20 名志愿者中每月志愿服务时长超过10小时的人数,求P(Z≥1)(结果精确到0.001),以及Z的数学期望(结果精确到0.01)。

参考数据：4.05,0.598 720≈0.000 035,0.729 120≈0.001 8,0.773 420≈0.005 9。若Y～N(0,1),则P(Y≤0.25)≈0.598 7,P(Y≤0.61)≈0.729 1,P(Y≤0.78)≈0.773 4。

解析：(1=6×0.02+7×0.10+8×0.20+9×0.38+10×0.18+11×0.08+12×0.04=9。

s2=(-3)2×0.02+(-2)2×0.10+(-1)2×0.20+12×0.18+22×0.08+32×0.04=1.64。

(2)(i)由题意并结合(1)可知,μ=9,σ2=1.64≈1.282。

(ii)由(i)可知,P(X＞10)=1-P(X≤10)≈0.226 6,故Z～B(20,0.226 6)。

因此,P(Z≥1)=1-P(Z=0)=1-(1-0.226 6)20≈1-0.005 9≈0.994,E(Z)=20×0.226 6≈4.53。