横向过载下考虑颗粒聚合行为的颗粒阻尼特性研究①
杨文婧,吴学婷,刘贝贝,刘佩进
(1.西北工业大学 航天学院,燃烧、热结构与内流场重点实验室,西安 710072;2.中国空空导弹研究院,洛阳 471009)
0 引言
近年来由于导弹突防能力需求的不断提升,高机动性能下的固体火箭发动机需要承受复杂的过载状况,因此需要提升发动机工作时的安全性和可靠性。通常为了提高发动机的比冲、抑制燃烧不稳定性,同时增加装药的能量,需要采用含铝复合推进剂,燃烧后产生的大量Al2O3凝相颗粒,形成复杂的发动机两相流系统。发动机中凝相颗粒在过载力作用下,会发生偏移聚集行为,增加了颗粒之间的碰撞概率,更容易产生大粒径的颗粒。固体火箭发动机中存在多种增益与阻尼因素,主要的增益因素包括推进剂的燃烧增益、声涡耦合,主要的阻尼因素包括粒子阻尼、喷管阻尼等,是否会出现不稳定现象并维持压强振荡是各种因素综合作用的结果。
王国辉等[1]对有过载和无过载多种工况下发动机内流场进行了计算,得出了气相及颗粒相在过载条件下的流动特性,气相受横向过载的影响不大,而凝相颗粒的粒径越大,受过载的影响越大。SABNIS等[2]认为粒径在50 μm以下的颗粒受气相流场的影响大于横向过载的影响,50 μm以上受过载的影响较大,在过载力作用下其运动轨迹发生改变,向发动机承载一侧偏移,加剧凝相粒子之间的碰撞以及凝相粒子与壁面之间的碰撞。田维平等[3]总结了粒子间碰撞与粒壁碰撞的规律,其中,不同粒径的液滴相互碰撞的结果可能为反弹、聚合及破碎等,导致液滴粒径分布发生变化;而液滴碰撞壁面机制一般依据韦泊数(We)大小,分为吸附、反弹、展成液膜及飞溅等四种结果,在燃烧室中产生的Al2O3液滴与壁面之间主要表现为吸附与反弹共存;而在喷管收敛段的主要表现为反弹。武渊等[4]认为由于过载对凝相颗粒分布的影响导致燃烧室内的温度场发生畸变,温度最高点发生在药柱后段与绝热层连接部位,该处流场的温度达到了4000 K以上。许团委等[5]采用欧拉-拉格朗日模型对过载下战术发动机的内流场进行了数值仿真,研究表明凝相颗粒受横向过载的影响易在发动机承载面的绝热层表面沿着流场方向形成一条粒子浓度缓慢增大的聚集带。苗琳[6]计算了多种过载形式下发动机内的两相流场,其中,横向过载以及轴向过载易导致凝相颗粒在发动机承载面以及后封头处沉积,当过载较小时,适当的转速可减少承载面和后封头处的粒子浓度。刘长猛等[7]的研究表明随着轴向过载的增大,凝相粒子在发动机内部的驻留时间会减小。刘中兵等[8]认为在横向长时间中小过载下,在凸起较大的人脱根部和后接头拐弯处因凝相粒子流聚集会出现较大的烧蚀坑,烧蚀极不均匀,易发生烧穿故障,应在结构型面设计中避免较大的台阶出现。WANG 等[9]的研究表明随着横向过载的增大,喷管喉部处的颗粒浓度几乎呈线性增加,导致喷管喉道的异常烧蚀急剧恶化。王立武等[10]对典型喉衬材料抗高横向过载烧蚀性能进行了研究,研究认为因颗粒冲刷引起的机械侵蚀的加剧是导致喉部偏烧蚀的主要原因,在高横向过载下,轴编C/C抗过载烧蚀性能最好。张翔宇等[11]通过建立固体发动机火箭橇地面过载模拟试验方法,复现了飞行过载诱发的发动机不稳定燃烧现象。之后,张翔宇等[12]通过对故障发动机开展试验研究,验证了导弹飞行过载是引起发动机不稳定燃烧的最主要原因。横向过载会使颗粒的浓度发生改变,承载一侧聚集大量的大粒径颗粒,而另一侧只有一些随流性好的小颗粒。檀叶等[13]利用不稳定燃烧线性理论分析认为过载引起的颗粒浓度分布变化是引起不稳定燃烧的关键因素。游艳峰等[14]通过离散元法得出在横向过载条件下,颗粒的非均匀分布式燃烧会使粒子阻尼减小,对发动机的稳定性十分不利。在发动机中,高浓度区域粒子阻尼增大,而低浓度区域粒子阻尼减小。30 μm以内的粒子在过载下粒子阻尼基本不变;较大的粒子在大横向过载下,极短时间(5 ms)后粒子阻尼开始减小,且粒径越大的粒子其阻尼减小得越早、越快。刘佩进等[15]总结了固体火箭发动机中燃烧不稳定现象的研究进展,提出了横向过载会改变发动机内凝相颗粒的分布,影响颗粒的阻尼效应,同时颗粒空间分布的改变也会使燃烧室内铝粒子燃烧释热区域发生变化,易导致热声不稳定。
横向过载会改变固体火箭发动机内凝相粒子原有的运动轨迹,增大颗粒与颗粒,颗粒与壁面的碰撞概率,改变凝相粒子的粒径和浓度分布,使颗粒的阻尼特性发生变化,造成发动机的燃烧不稳定。故而,研究横向过载下Al2O3的聚合行为以及其对颗粒阻尼的影响具有很大的意义。
1 数值模型
本文考虑彻体力作用下燃烧室凝相颗粒运动过程,分析并获得彻体力对凝相颗粒运动规律、相互作用规律和空间动态分布的影响,因此选择燃烧室作为计算区域。考虑颗粒数量会很大程度地影响计算量,采用一定比例缩小的圆柱形几何模型来代替发动机燃烧室模型,模型长度330 mm,直径55 mm,如图1所示。
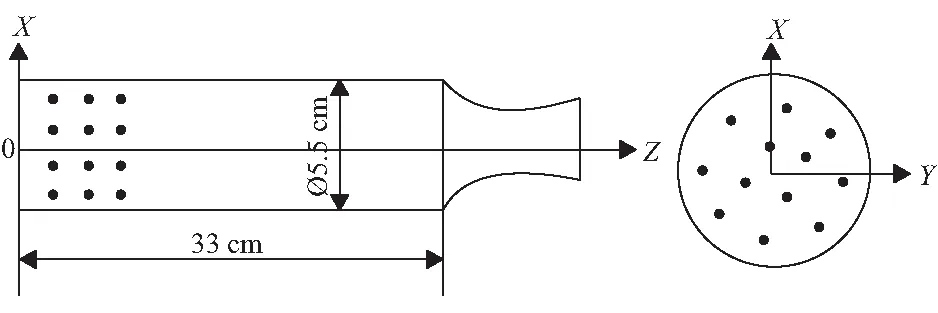
图1 计算几何模型图
1.1 数值方法
1.1.1 气相控制方程
气相控制方程是基于连续介质流场进行求解计算,主要的控制方程是连续方程和动量方程,见式(1)、式(2)所示。
连续方程:
(1)
动量方程:
(2)
1.1.2 颗粒相控制方程
以单个颗粒为研究对象进行分析,则其运动方式一般情况下可以分为平动和转动。离散元模型中,单个颗粒的运动主要由牛顿第二定律控制进行的,见式(3)、式(4)所示。
平动方程:
(3)
转动方程:
(4)
1.1.3 气固耦合模型
在固体发动机中,凝相颗粒将在燃气的拖曳作用下运动,此时气相也会受到颗粒相的反作用力,两者之间将会出现动量传递,两相流中颗粒相与气相的双向耦合主要通过动量传递实现。气固两相流耦合计算流程示意图如图2所示。
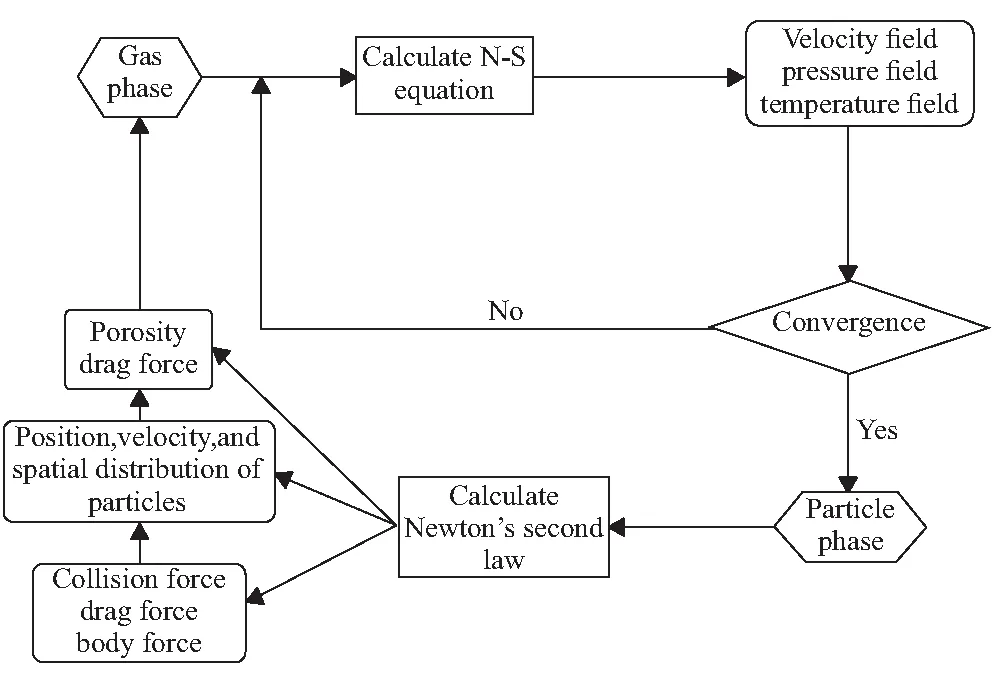
图2 气固两相流耦合计算流程示意图
本文所采用的CFD-DEM气固耦合计算流程如下:
(1)给定一个初始的气相流场,待气相流场收敛后,给定初始颗粒位置、粒径等信息,然后在一个时间步长内,计算颗粒与颗粒、颗粒与壁面的作用力、流体曳力以及彻体力等作用力,基于DEM方法计算出颗粒新的位置、速度等信息;
(2)将DEM方法所得颗粒位置、粒径及颗粒数等信息应用于流体网格内计算出流体网格的孔隙率以及流体的曳力,在孔隙率和流体曳力已知情况下,再次利用N-S方程计算新的流场信息,待流场收敛后重新迭代计算颗粒相信息;
(3)交替求解颗粒相与气相的控制方程,求得两相流中颗粒相的运动过程。
1.2 粒子碰撞聚合模型
通过对飞行试验以及地面模拟过载试验中发动机内颗粒粒度的测量,发现发动机颗粒在过载状态下粒径值大于地面静止环境时所测值,产生大粒径颗粒的概率显著增加,因此很有必要考虑过载下颗粒之间相互碰撞引起颗粒聚合行为对发动机中凝相颗粒粒径改变的影响以及获取此时颗粒的运动规律。
针对液滴碰撞规律相关学者已开展了大量的理论、实验及数值模拟研究,然而不同的研究对象其碰撞规律却不尽相同,尤其高表面张力、高粘度的Al2O3颗粒之间的碰撞,其碰撞规律和水、煤油之间有较大的差别。Al2O3凝相颗粒在固体火箭发动机中处于高温高压环境下,因此很难针对此状态下的颗粒展开颗粒间碰撞聚合实验研究。西北工业大学夏盛勇等[16]基于VOF方法、利用开源程序Gerris建立了Al2O3颗粒之间的碰撞模型,为本文建立颗粒间碰撞聚合模型提供了数值研究基础。
本文中颗粒间碰撞等效图,如图3所示。
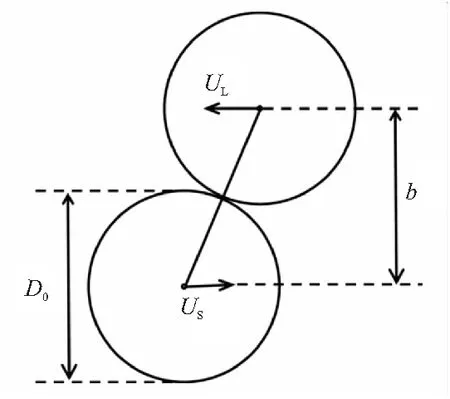
图3 颗粒碰撞等效图
本文中颗粒间的碰撞规律主要由韦伯数和碰撞参数控制,见式(5)和式(6)所示。
韦伯数:
(5)
碰撞参数:
(6)
根据文献[7]可知,随着韦伯数和碰撞参数的变化,颗粒与颗粒之间碰撞后会发生微小变形后聚合、反弹、大变形后聚合、自反分离以及拉伸分离等运动行为,对应的判别公式见式(7)~式(11)所示。
微小变形后聚合:
(7)
(8)
反弹:
(9)
自反分离:
(10)
拉伸分离:
(11)
大变形后聚合:介于其他区域之间。
由式(7)~式(11)可知,不同的韦伯数、碰撞参数下,颗粒在碰撞后将会有不同的运动行为。上述碰撞结果又可分为两部分进行研究:第一部分是微小变形后聚合行为,此情况发生在韦伯数很低的情况下,当给定颗粒直径、颗粒密度以及颗粒表面张力等参数时,韦伯数仅与颗粒间相对速度有关,因此微小变形后聚合行为主要发生在颗粒间相对速度很低的情况;第二部分包括反弹、大变形后聚合、自反分离和拉伸分离等行为,颗粒间相对速度较高。
根据式(7)~式(11),可得本文颗粒碰撞模型图。由于上述两种情况对应的韦伯数差别较大,这里分别给出对应的碰撞模型图,如图4所示。由图4可知,Al2O3颗粒碰撞后发生的微小变形后聚合行为主要发生在韦伯数小于0.2的情况下,当颗粒间相对速度很低时,便会出现微小变形后聚合行为;随着韦伯数的增大,会相继出现反弹、大变形后聚合、自反分离以及拉伸分离等行为,此时颗粒间相对速度会较大一些。
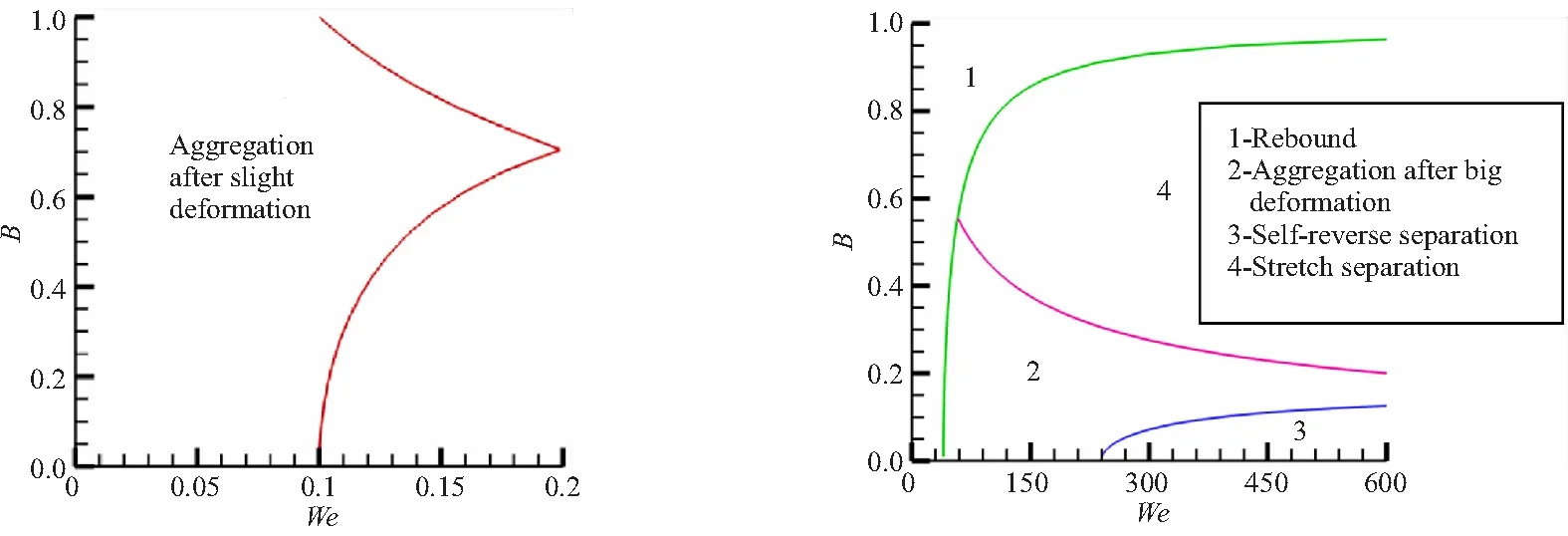
(a)Small Weber numbers (b)Large Weber numbers
由式(7)~式(11)可知,随着颗粒碰撞后韦伯数和碰撞参数的不同,颗粒碰撞后的运动行为可分为微小变形后聚合、反弹、大变形后聚合、拉伸分离以及自反分离等行为;由式(5)、式(6)可知,韦伯数和碰撞参数主要与颗粒的密度、颗粒间相对速度、颗粒直径、颗粒的表面张力以及颗粒碰撞时的角度有关。
综上可得粒子碰撞模型的嵌入方法:
(1)由气相程序计算一个初步的流场,凝相颗粒在气相曳力作用下移动,由其他已知信息可得此状态下每个颗粒在给定时间步下实时的位置、线速度、旋转角速度、颗粒粒径等信息。
(2)由颗粒的位置信息来判断颗粒间接触状态。当两个颗粒中心间距大于等于两个颗粒半径之和时,颗粒跳出碰撞模型计算模块,保持原来的状态进入下一步计算模块;当两个颗粒中心间距小于两个颗粒半径之和时,进入颗粒碰撞模型计算模块。
(3)当两个颗粒中心间距小于两颗粒半径之和时,首先根据两个颗粒的位置信息和速度信息计算出颗粒间的碰撞参数B,然后由颗粒的密度、相对速度、颗粒直径以及表面张力等信息计算出颗粒的韦伯数We,接着由式(7)~式(11)计算该碰撞参数B下对应的临界微小变形后聚合韦伯数、临界反弹韦伯数、临界大变形后聚合韦伯数、临界自反分离韦伯数以及临界拉伸分离韦伯数等,通过比较该碰撞状态下的韦伯数与临界韦伯数确定颗粒碰撞后的运动行为。
(4)当颗粒的韦伯数在图4(a)所示曲线的左侧时,颗粒碰撞后发生微小变形后聚合行为;当颗粒的韦伯数处于图4(b)所示的1区域时,颗粒碰撞后发生反弹行为;当颗粒的韦伯数处于图4(b)的2区域时,颗粒碰撞后发生大变形后聚合行为;当颗粒的韦伯数处于图4(b)的3区域时,颗粒碰撞后发生自反分离行为;当颗粒的韦伯数处于图4(b)的4区域时,颗粒碰撞后发生拉伸分离行为。由于固体火箭发动机燃烧室中凝相颗粒间的相对速度较低,颗粒的韦伯数也比较低,因此颗粒碰撞后运动行为基本为微小变形后聚合和反弹行为。
(5)当颗粒碰撞后发生微小变形后聚合行为时,本文拟采用“两个颗粒碰撞后聚合为一个颗粒”的方法。由体积守恒定律、质量守恒定律和动量守恒定律计算出新的颗粒的位置、直径及速度等信息。
(6)当颗粒碰撞后发生反弹行为时,根据颗粒运动控制方程计算出颗粒碰撞后的物性参数。
(7)循环计算整个计算域内的颗粒,依次判断每两个颗粒间的碰撞状态,根据碰撞时颗粒的韦伯数和碰撞参数确定颗粒碰撞后的运动行为,最后可得该时间步下所有颗粒的碰撞运动结果。
(8)最后迭代计算整个程序,直至要求的时间步下结束程序。
当固体火箭发动机处于高过载状态时,颗粒会由于过载的作用而发生横向偏移,从而增加了颗粒的空间浓度,对应的颗粒间碰撞概率会显著提高,此时不同颗粒碰撞时对应的韦伯数和碰撞参数不同,因此会有不同的碰撞结果。本文针对彻体力作用的固体火箭发动机燃烧室展开颗粒碰撞数值模拟研究,拟得到考虑颗粒碰撞聚合的两相流模型以及对应的凝相颗粒运动规律。
1.3 粒子阻尼算法
在常规状态下时,发动机中颗粒处于均匀分布状态,此时发动机声场为为小扰动,可利用Culick微粒松弛理论计算粒子阻尼大小,即通过压力振幅的时间衰减常数αp来表征粒子阻尼大小,见式(12)~式(14)所示。
(12)
(13)
(14)
从式(12)~式(14)可知,影响颗粒阻尼值的因素可分为两部分:第一部分与粒子空间分布有关,即单位体积中粒子质量分数越大时,颗粒阻尼值越大;第二部分与颗粒相和气相的物性参数有关,主要包括粒子直径、粒子密度、声振荡频率及气相动力粘度等参数。
当固体火箭在作机动飞行时,其发动机会受到飞行过载的作用,此时发动机燃烧室内凝相颗粒会发生偏移聚集行为,一方面改变了凝相颗粒在燃烧室的空间分布状态,形成局部的低浓度区域及高浓度区域,从而通过颗粒的局部质量分数改变了颗粒的阻尼值;另一方面,当考虑颗粒碰撞聚合行为时,颗粒的粒径会发生改变,微粒的动力松弛时间和热松弛时间也都会改变,从而过载通过影响颗粒的粒径来改变颗粒的阻尼值。因此,过载下不同局部区域颗粒的阻尼值不一致,通过整个发动机内颗粒的平均质量分数及颗粒的初始平均粒径值来计算颗粒阻尼值是不准确的,且不能表征不同粒径下颗粒空间分布不均匀性引起的阻尼值的改变。
针对上述两方面的影响,本文拟通过引入与空间分布相关的权重函数来对粒子阻尼值进行,即粒子阻尼值表征颗粒空间分布不均匀情况以及发动机凝相颗粒聚合引起粒径变化情况下凝相颗粒的阻尼值。基本思路是:先将计算域划分为n个小区域,然后计算每个区域内颗粒的阻尼值,最后对每个区域进行加权平均,从而得到粒子阻尼值。
对于给定的网格i,该区域内颗粒数为m,该区域颗粒的阻尼值为αpi,见式(15)所示:
(15)
根据网格大小对每个网格的颗粒阻尼值αpi进行加权平均,从而得到燃烧室内粒子阻尼值αpn,见式(16)所示:
(16)
由此可得考虑颗粒粒径变化及空间分布不均匀情况下颗粒的粒子阻尼值αpn,见式(17)所示:
(17)
2 结果与分析
2.1 网格无关性验证
为了检验网格数对粒子阻尼值的影响,本文对横向过载30g的颗粒运动结果进行后处理计算,得到网格数分别为26 480、87 840、206 800、401 200网格数下粒子阻尼值,如图5所示。由图5可知,不同网格数下颗粒的粒子阻尼值随时间的变化趋势基本一致,因此考虑颗粒空间分布及粒径变化的粒子阻尼值可表征凝相颗粒在过载下的阻尼值变化情况。
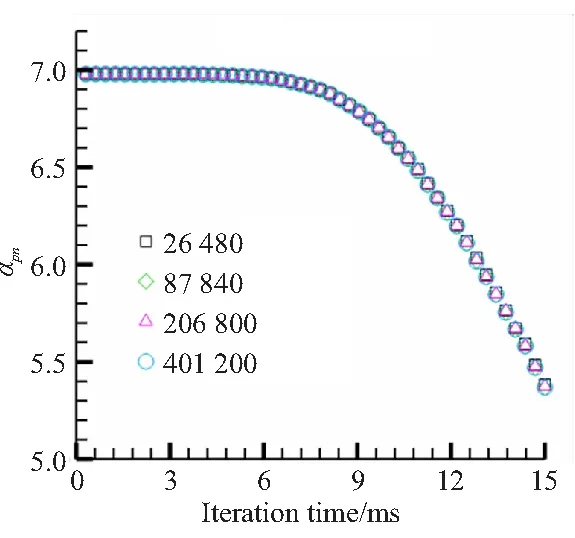
图5 网格数对粒子阻尼值的影响
2.2 粒子配位数
横向过载会引起颗粒的横向偏移,而不同横向过载对颗粒横向偏移的影响程度是不同的,所以颗粒的空间位置分布也不一致,因此给出不同横向过载下粒子配位数图,如图6所示。由图6可知,当横向过载为10g时,颗粒沿X向偏移较少,其在远离壁面区域的粒子配位数基本都低于26,而在近壁面区域中,颗粒的粒子配位数增大,达到60左右的颗粒数很少,且集中在中心区域;当横向过载为20g时,与10g的横向过载偏移相比,其偏移略高,颗粒在远离壁面区域的粒子配位数变化不大,均低于26,而在近壁面区域中,粒子配位数为60左右的颗粒数增大,且沿着过载壁面中心区域向两边扩散分布;当横向过载为30g时,颗粒沿X向偏移较多,其在远离壁面区域的粒子配位数仍在26以下,而在近壁面区域中,粒子配位数为60左右的颗粒数进一步增大,且沿着整个过载面离散分布;当横向过载为40g时,颗粒沿X向偏移最多,其在远离壁面区域的粒子配位数仍旧低于26,而在近壁面区域中,粒子配位数为60左右的颗粒数与30g的横向过载情况相比变化不大,且沿着整个过载面离散分布。
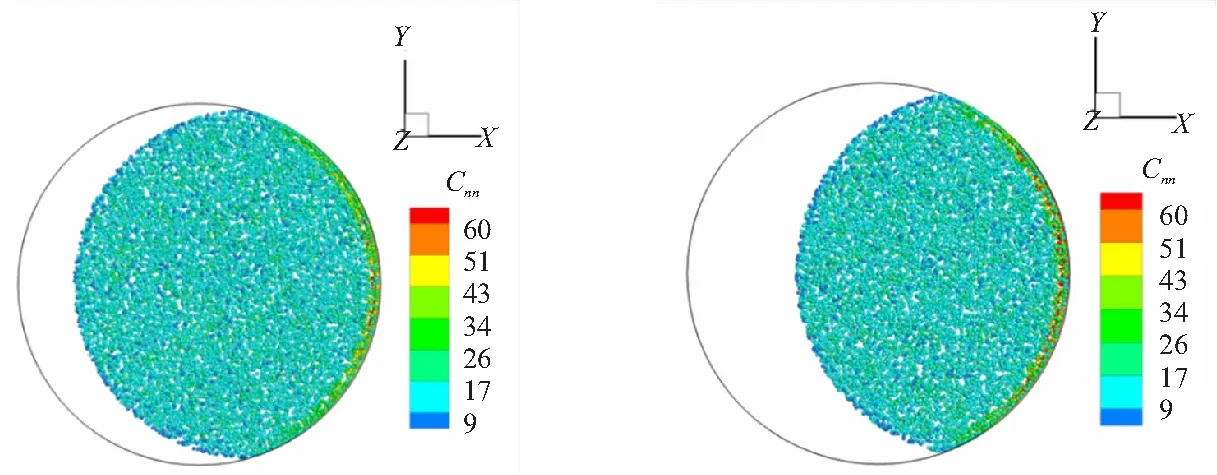
(a)Lateral overload=10g (b)Lateral overload=20g
因此,随着横向过载的增大,颗粒的横向偏移会越来越大,在远离壁面区域颗粒的粒子配位数基本一致,在近壁面区域颗粒的粒子配位数会显著增大。故横向过载是影响近壁面区域颗粒聚集程度的重要因素。
2.3 颗粒间碰撞概率
不同横向过载下,凝相颗粒所受的彻体力不同,导致颗粒的横向偏移量有较大差别,颗粒的空间聚集程度也不同,所以对应的颗粒间碰撞概率会有很大的差异性。不同横向过载下颗粒间碰撞概率随时间的变化过程图如图7所示。
由图7可知,当横向过载为10g时,6 ms时刻后发生颗粒碰撞,大部分时刻下颗粒间的碰撞概率约为 0.000 065,少许时刻下颗粒间碰撞概率为0.000 13左右,颗粒间的碰撞概率基本不随时间变化;当横向过载为20g时,3.6 ms时刻后发生颗粒碰撞,大部分时刻下颗粒间的碰撞概率在0.000 065~0.000 073之间,部分时刻下颗粒间的碰撞概率在0.000 13~0.000 15之间,少部分时刻下颗粒间的碰撞概率在0.000 2左右,颗粒间碰撞概率会随着时间略微增加;当横向过载为30g时,3.6 ms时刻后发生颗粒碰撞,大部分时刻下颗粒间的碰撞概率在0.000 065~0.000 11之间,部分时刻下颗粒间的碰撞概率在0.000 13~0.000 18之间,少部分时刻下颗粒间的碰撞概率为0.000 2~0.000 3之间,颗粒间碰撞概率随时间呈现递增的趋势;当横向过载为40g时,2.4 ms时刻后发生颗粒碰撞,大部分时刻下颗粒间的碰撞概率在0.000 065~0.000 11之间,部分时刻下颗粒间的碰撞概率在 0.000 13~0.000 2之间,少部分时刻下颗粒间的碰撞概率在0.000 2~0.000 34之间,且颗粒间碰撞概率随时间递增趋势更加明显。
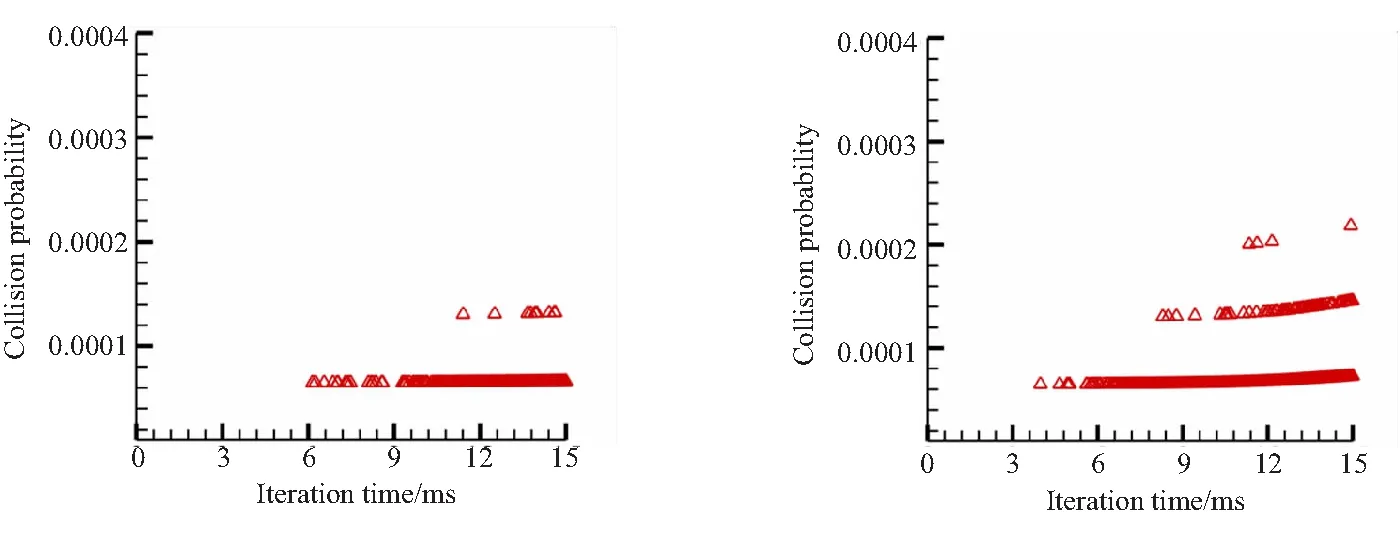
(a)Lateral overload=10g (b)Lateral overload=20g
当横向过载较小时,颗粒群的聚集程度较小,导致颗粒间的碰撞概率较小,且碰撞概率随时间变化较慢;随着横向过载逐渐增大,颗粒群的聚集程度增大,导致颗粒间的碰撞概率明显增大,且碰撞概率随时间增加趋势更加明显,故横向过载大小是影响颗粒间碰撞概率的重要因素。
2.4 粒子阻尼
颗粒空间分布状态的改变及颗粒粒径的改变皆可以引起颗粒阻尼值的改变,因此给出不同横向过载下颗粒的粒子阻尼系数及粒子阻尼值,如图8所示。
由图8可知,不同过载下初始时刻颗粒阻尼系数为1.0,粒子阻尼值为6.98,阻尼系数和粒子阻尼值都随着时间逐渐降低,且变化趋势一致。当横向过载为10g时,颗粒阻尼系数和粒子阻尼值随时间变化很小;当横向过载为20g时,15 ms时刻粒子的阻尼系数为0.9、粒子阻尼值为6.3,阻尼系数和粒子阻尼值变化率都是10%;当横向过载为30g时,15 ms时刻粒子的阻尼系数为0.78、粒子阻尼值为5.4,阻尼系数和粒子阻尼值变化率都是22%;当横向过载为40g时,15 ms时刻粒子的阻尼系数为0.63、粒子阻尼值为4.4,阻尼系数和粒子阻尼值变化率都是37%。
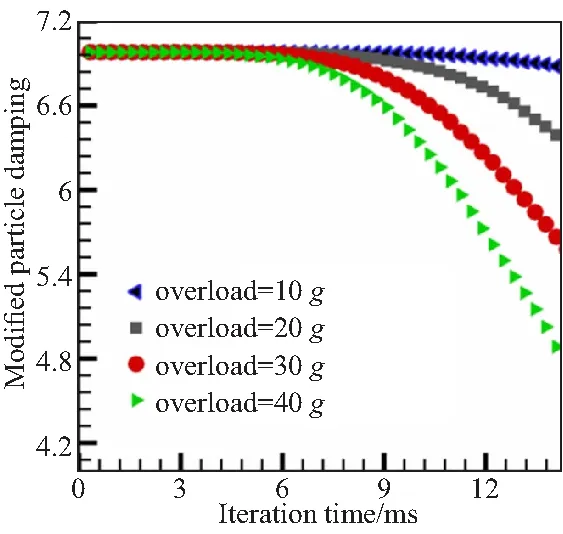
图8 粒子阻尼值
由此可知,在相同横向过载下,颗粒的阻尼系数和粒子阻尼值随时间变化规律是一致的,而不同横向过载下,由于颗粒的空间分布状态以及粒径变化规律有很大的差异,所以颗粒的阻尼系数和粒子阻尼值变化规律明显不同,且随着横向过载的增大,阻尼系数和粒子阻尼值降低趋势更加明显。因此,向过载是影响颗粒阻尼系数和粒子阻尼值的重要因素。
3 结论
横向过载下,颗粒横向偏移显著增加,颗粒间的碰撞概率增大,并且碰撞概率随过载作用时间增加大幅度提高。颗粒间因碰撞聚合易生成的大粒径颗粒,大粒径颗粒的产生使得颗粒空间分布更具不均匀性,进而导致颗粒的阻尼值明显降低,最终影响发动机的燃烧稳定性。横向过载的大小对颗粒行为及发动机性能的影响规律:
(1)横向过载增大时,会显著地增加颗粒的横向偏移,且近壁面区域颗粒聚集程度显著增加;
(2)横向过载越大时,颗粒间的碰撞概率越大,且碰撞概率随时间增加的趋势更加明显;
(3)综合考虑颗粒横向偏移、颗粒数量以及颗粒粒径大小等因素,发现横向过载越大时,颗粒阻尼降低程度越大,发动机燃烧不稳定性越严重。

