生活中与气体性质有关的情景分析

■贵州省凯里市恒成高级中学 胡朝平

人们在日常生产生活中使用的器材,如压力罐与水泵和气泵连接供水系统、汽车减震装置、温度计、喷雾器、压力锅、中医拔罐设备、气球等,均涉及打气、抽气、漏气现象,这些都是典型的气体性质的具体应用。

一、压力罐与水泵和气泵连接供水系统

例1如图1所示为高楼供水系统的示意图,压力罐与水泵和气泵连接,其中压力罐的底面积为5 m2、高为6 m,开始时罐内只有压强为1.0×105Pa的气体,阀门K1、K2关闭。现启动阀门K3,水泵向罐内注水,当罐内气压达到2.4×105Pa时水泵停止工作,当罐内气压低于1.2×105Pa时水泵启动,假设罐内气体温度保持不变。

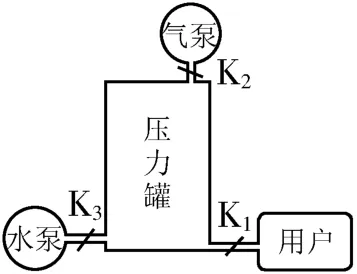
图1

(1)当罐内气压达到2.4×105Pa时,求注入水的体积。

(2)某一次停水,阀门K3关闭。当用户用水,使得罐内气压低至1.2×105Pa时,气泵启动。为保证剩余水全部供用户使用后,罐中气体的压强都不低于1.2×105Pa,求气泵至少要向罐内充入压强为1.0×105Pa的气体的体积。

解析：(1)设注入水的体积为V,根据玻意耳定律得p0V0=p(V0-V),其中p0=1.0×105Pa,V0=5×6 m3=30 m3,p=2.4×105Pa,解得V=17.5 m3。

(2)设充入气体的体积为V',则p0(V0+V')=p'V0,解得V'=6 m3。

点评:选罐内一定质量的气体为研究对象,气体做等温变化,确定气体在始末状态下的p1、V1及p2、V2,根据玻意耳定律列式求解。

二、汽车减震装置

例2如图2所示是由汽缸、活塞柱、弹簧和上下支座构成的汽车减震装置,该装置的质量、活塞与汽缸壁之间的摩擦均可忽略不计,汽缸的导热性和气密性良好。该装置未安装到汽车上时,弹簧处于原长状态,汽缸内的气体可视为理想气体,压强p1=1.0×105Pa,封闭气体柱和活塞的长度均为l=0.20 m。活塞的横截面积S=1.0×10-2m2。将该装置竖直安装到汽车上后,其承载的力F=3.0×103N 时,弹簧的压缩量Δx=0.1 m。大气压强恒为p0=1.0×105Pa,环境温度不变。求该装置中弹簧的劲度系数k。

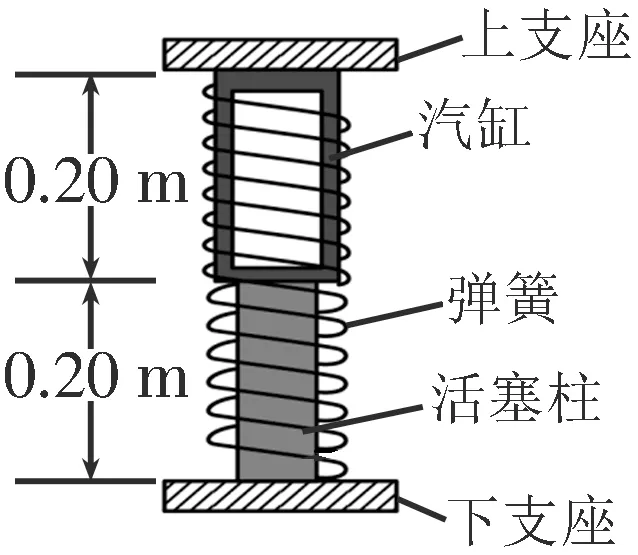
图2

解析：设该装置未安装到汽车上时,汽缸内封闭气体柱的长度为l,体积为V1;将该装置竖直安装到汽车上后,汽缸内封闭气体的压强为p2,体积为V2。则p1=p0,V1=lS,V2=(l-Δx)S。汽缸内封闭气体在安装在汽车上前、后做等温变化,根据玻意耳定律得p1V1=p2V2。对上支座进行受力分析,设汽车对上支座的压力为F,根据平衡条件得p2S+kΔx=p0S+F。联立以上各式解得k=2×104N/m。

点评:选汽缸内一定质量的气体为研究对象,气体做等温变化,确定气体在始末状态下的p1、V1及p2、V2,根据玻意耳定律列式求解;选上支座为研究对象,根据平衡条件列式求解。

三、温度计

例3有人设计了一种测温装置,其结构如图3所示。玻璃泡A内封闭有一定质量的气体,与玻璃泡A相连的B管插在水银槽中,管内水银面的高度x可反映玻璃泡A内气体的温度,即环境温度,并可由B管上的刻度直接读出。设B管的体积与玻璃泡A的体积相比可忽略不计。

图3

(1)在标准大气压下对B管进行温度刻度(标准大气压相当于76 cm 水银柱产生的压强),已知温度t1=27 ℃的刻度线对应管内水银面高度x1=16 cm,则t=0 ℃的刻度线对应的管内水银面高度x为多少？

(2)若大气压已变为相当于75 cm 水银柱产生的压强,利用该装置测量温度时所得读数仍为27 ℃,则此时的实际温度为多少？

解析：(1)B管的体积与玻璃泡A的体积相比可忽略不计,则玻璃泡A内封闭气体做等容变化,根据查理定律得,其中p1= (76 - 16)cmHg=60 cmHg,T1=(273+27)K=300 K,T=273 K,解得p=54.6 cmHg,水银柱产生的压强px=(76-54.6)cmHg=21.4 cmHg,则x=21.4 cm。

(2)玻璃泡A内封闭气体做等容变化,此时玻璃泡A内气体的压强p'=(75-16)cmHg=59 cmHg,此时的实际温度T'=,解得T'=295 K=22 ℃。

点评:因为B管的体积与玻璃泡A的体积相比可忽略不计,所以玻璃泡A内封闭气体做等容变化,根据查理定律列式求解。

四、打气(灌气)、抽气与漏气现象

打气(灌气)、抽气与漏气问题都属于变质量问题。分析变质量问题时,可以通过巧妙选择合适的研究对象,将变质量问题转化为定质量问题,再应用气体实验定律或理想气体状态方程列式求解。

1.打气(灌气)。

例4在抗击新冠肺炎疫情期间,很多公共场所采用压缩式喷雾器来消毒。如图4所示,喷雾器药液桶的总容积为V0,初始时,进液口和喷液口均关闭,桶内药液上方空气的压强为3p0,体积为。打开喷液口,喷洒消毒液,一段时间后关闭喷液口,此时药液桶内空气的压强为2p0。不考虑打气筒与药液桶连接管内空气的体积,整个过程视为等温变化过程,大气压强为标准大气压强p0。

图4

(1)关闭喷液口时,已喷出的消毒液体积是多少？

(2)每次打气,能打入压强为p0、体积为的空气,为了使药液桶内空气压强不小于3p0,至少需要打气多少次？

解析：(1)选药液桶内封闭气体为研究对象,气体做等温变化,根据玻意耳定律得,解得。

(2)选打气n次后药液桶内的气体为研究对象,气体做等温变化,根据玻意耳定律得解得n=10。

点评:打气时,活塞每推动一次,就把压强为p0、体积为V0的气体压入容器内,若活塞工作n次,就是把压强为p0、体积为nV0的气体压入容器内,容器内原有压强为p0、体积为V的气体,以容器内原有气体和即将打入的气体为研究对象,根据玻意耳定律p0(V+nV0)=p'V可解得。

2.抽气。

例5如图5所示,A、B是两个容积均为V的容器,用一只气筒C与它们相连,气筒C内有密封良好的可自由移动的活塞,气筒C的容积为。a、b是两只单向进气阀,当气筒抽气时a打开、b关闭,当气筒打气时b打开、a关闭。最初A、B两容器内空气的压强均为p0,活塞位于气筒C的最右侧。已知活塞从气筒C的最右侧运动到最左侧完成一次抽气,从最左侧运动到最右侧完成一次打气(活塞的体积和气筒与容器间连接处的体积不计,气体温度保持不变),求:

图5

(1)第一次抽气结束后气筒C内气体的压强p1。

(2)完成抽气、打气各2次后,A、B两容器内的气体压强之比。

解析：(1)第一次抽气过程中,选容器A内封闭气体为研究对象,气体做等温变化,根据玻意耳定律得,解得。

(2)第二次抽气过程中,选容器A内剩余气体为研究对象,根据玻意耳定律得p1V=;第一次打气过程中,选容器B内封闭气体为研究对象,同理得p2V;第二次打气过程中,选容器B内全部气体为研究对象,同理得。联立以上各式解得pA∶pB=2∶7。

点评:抽气时,气体的体积从V膨胀为V+V0,容器中的气体压强减小,活塞推动时,将抽气筒中体积为V0的气体排出,再次拉动活塞时,又将容器中剩余气体的体积从V膨胀到V+V0,容器中的气体压强继续减小,第一次抽气结束容器内气体的压强p1=,第二次抽气结束容器内气体的压强,活塞工作n次,则。

3.漏气。

例6一个瓶子里装有空气,瓶上有一个小孔跟外面大气相通,原来瓶里气体的温度是7 ℃,若把它加热到47 ℃,则瓶里留下空气的质量与原有空气质量之比为____。

解析：设瓶子的容积为V,初始状态下V1=V,T1=(273+7)K=280 K,末状态下V2=V+ΔV,T2=(273+47) K=320K。选瓶里原有气体为研究对象,气体做等压变化,根据盖-吕萨克定律得,解得。

答案：

点评:漏气问题,不管是等温漏气、等容漏气,还是等压漏气,都要将漏掉的气体“收”回来。可以设想有一个“无形弹性袋”收回漏气,且漏掉的气体和容器中剩余气体同温、同压,这样就把变质量问题转化为定质量问题,然后应用气体实验定律列式求解即可。

五、气球类问题

例7一个热气球的体积为V,内部充有温度为Ta的热空气,气球外冷空气的温度为Tb。已知空气在1个标准大气压、温度为T0时的密度为ρ0,该气球内、外的气压始终都是1个标准大气压,重力加速度为g。

(1)求该热气球所受浮力的大小。

(2)求该热气球内空气所受的重力。

(3)设充气前热气球的质量为m0,求充气后它还能托起的物体的最大质量。

解析：(1)设1个标准大气压下质量为m的空气在温度为T0时的体积为V0,密度温度为T时的体积为VT,密度ρT=根据盖-吕萨克定律得解得热气球所受的浮力F=ρTbgV,解得。

(2)热气球内空气所受的重力G=ρTaVg,解得。

(3)设该热气球还能托起的物体的最大质量为M,根据平衡条件得Mg=F-Gm0g,解得。

点评:以热气球内的全部气体为研究对象,根据盖-吕萨克定律、阿基米德定律、密度公式、力的平衡条件进行分析求解。

总结：气体问题涉及一部分气体或两部分气体或变质量气体,解决此类问题的关键是分析清楚一定质量气体初、末状态的压强p、体积V和温度T三个参量。封闭气体的压强,不仅与气体的状态变化有关,还与相关的水银柱、活塞、汽缸等物体的受力情况和运动状态有关,解决这类问题的关键是明确研究对象,分析研究对象的受力情况和运动情况,列动力学关系式,求得封闭气体的压强。