规则波作用下养殖网箱水动力特性分析

王银涛,王 千,2,郭晓宇,2,3

(1上海交通大学船舶海洋与建筑工程学院,上海 200240;2 上海交通大学水动力学教育部重点实验室,上海 200240;3 中国水产科学研究院渔业机械仪器研究所,上海 200092)

随着环境保护意识的日渐强烈和人们对海产品需求的日益增加,近岸水产品养殖以及捕捞业不能满足需求与环境保护的平衡,发展深远海养殖可为渔业养殖提供新的养殖手段[1]。中国海岸线漫长、深远海水域辽阔,这为大力发展深远海网箱养殖提供了得天独厚的自然条件[2]。但由于离岸深水区域海况复杂且外海网箱无防浪建筑物的遮挡保护,深远海渔业养殖平台面临严峻的环境考验[3-4],平台建设需考量网箱在风浪场作用下的安全性。

养殖网箱的框架杆件和网衣的网绳都可以视为小尺度结构物,而莫里森(Morison)公式被广泛应用于确定作用在小尺度海工结构物上的波浪力[5]。基于莫里森公式,单柱结构波浪作用下阻力系数与惯性力系数变化规律已有大量研究[6-10]。由单桩组成的群桩基础是海上建筑最常见的基础形式之一,小直径桩常以群桩的形式出现在海洋工程建筑物中,其在波浪作用下群桩中各组成桩的受力与单桩有较大的差别,引起变化的原因被称之为群桩效应[11]。国内外学者对单桩和群桩效应进行了探究并总结了群桩效应除与几何因素有关外,还与波要素及波态(规则波或不规则波)有关[12-15]。曲金哲等[16]根据一些桩基结构的波向力试验结果,同时考虑桩和波浪的因素,提出了当量直径的概念,分析得到统一的无量纲不规则波波向力经验公式,并在此公式的基础上探究了群桩系数的变化规律。以上研究主要基于海洋工程中的桩基结构。网衣是网箱上的重要结构,多目结构产生的水动力特性与阻水效应受到研究者关注。国内外学者开展了刚性网衣水动力的试验研究,得到了波向力随波浪参数的变化规律[17-18]。也有研究考虑网的变形进行试验,进一步将网模型化为刚性圆杆铰接组成,通过莫里森公式计算杆件受力[19]。由于直接模拟大量网目结构存在困难,数值研究采用集中质量法、多孔介质模型、群化模型与欧拉-拉格朗日方法研究网衣的水动力特性与周围流场特性[20-24]。为了满足快速预报网衣受力需求,考虑网衣变形,采用莫里森公式建立了网衣水动力快速计算方法[25]。由于网箱组成的复杂性,国内学者开展了网箱结构在波浪、水流作用下水动力试验[26-27],并发现吃水深度和网衣都会对网箱在波浪载荷下的响应产生影响[28]。和试验研究相比,网箱水动力特性数值模拟研究进展较为滞后。近些年,有研究者采用计算流体力学方法(CFD)结合多孔介质模型模拟网箱附近的流场特征[29-31], 也有学者提出了网箱结构求解数值框架并对系泊网箱结构进行了数值模拟[32]。由于网箱的复杂性,目前多数数值模型还需试验率定与验证。

考虑到目前缺少网箱水动力与水动力相关参数的定量化关系,研究了规则波作用下网箱的水动力特性,获得了波向力随波浪参数的变化规律;将试验结果进行数据回归分析,采用当量直径为特征尺度修正Keulegan-Carpenter number(KC数),得到了无量纲力与细杆组合结构的截面特性和波浪特性之间的关系的经验公式。

1 试验方法

1.1 试验模型与试验设置

本研究中半潜式深海养殖网箱原型为边长45 m,高约38.5 m的正六边形棱柱。模型试验在上海交通大学教育部水动力学重点实验室的波浪水池中进行。水池总长42.4 m、宽4 m、高1.6 m,能够制造周期1～2 s,波高0～0.2 m的规则波。

试验模型依据重力相似准则,考虑到试验水池的尺寸,采用1∶100的网箱模型,网衣参考Lader的试验[17],选用孔隙率Sn=0.79的网衣。南海各区域内50年一遇极值波高在4～10 m之间[33-34],根据模型的缩比关系,本试验的工况设置采用波高2～10 cm、周期1～1.8 s的波浪,不同工况的波浪参数如表 1所示。

表1 试验中不同周期对应的波长Tab.1 Wavelength corresponding to different wave periods

图1给出了试验模型示意图。试验时,模型放到水池中轴线上,距造波机24 m。试验水深为50 cm,模型吃水深度(对应实际工况中的生存和工作两种模式)分别为32 cm和37 cm。

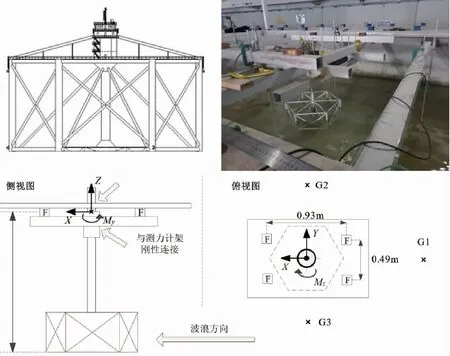
图1 模型试验示意图Fig.1 Schematic diagram of model experiment

测力装置采用4个KISTLER 9317C压电式三分力传感器,每个三分力传感器可以单独测量其所在位置力的3个分量。将传感器分别布置于测力天平架的4个对称位置,即可通过每个传感器的测量值得到模型所受到的总力和总力矩;波面变化用电容式浪高仪测得。为保证测量精度,试验对测量仪器进行标定与校验。浪高仪的标定通过浸没深度与信号放大器电压值的匹配校核获得标定系数。

测力传感器通过静态负荷加载校验,其水平力和垂向力的测量误差均小于1%。对系统进行了湿模态下的自振频率测定,结果表明模型测力系统的结构自振频率为6 Hz和9 Hz,满足波向力试验的基本要求。

2 结果与分析

2.1 网箱框架受力分析

对浪高仪的数据进行处理,并将预计理论波形与浪高仪所测数据进行对比(图2)。二阶斯托克斯波波面和浪高仪所测得的波面基本一致,因此数值计算的波浪理论采用二阶斯托克斯波。

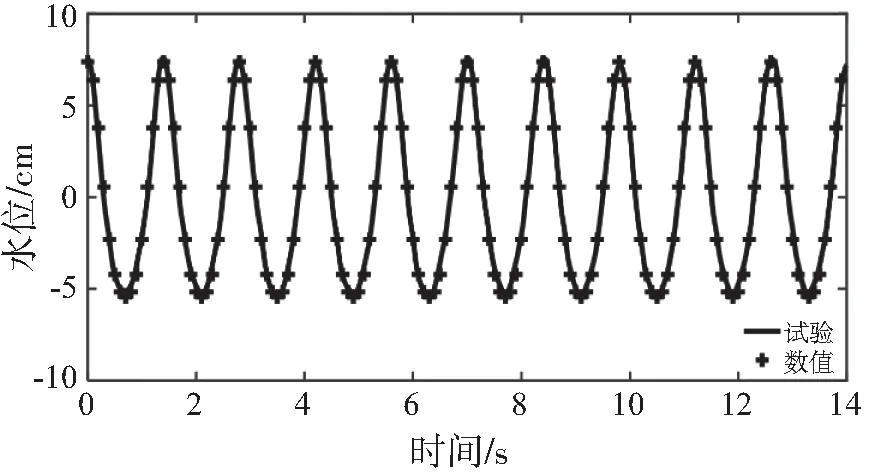
图2 二阶斯托克斯波与浪高仪测得的波形对比Fig.2 Comparison of wave profile measured by second-order Stokes wave and wave height

本试验研究了吃水32 cm和37 cm两种情况下网箱框架受力,不同波况下网箱波向力最大值如表2所示。

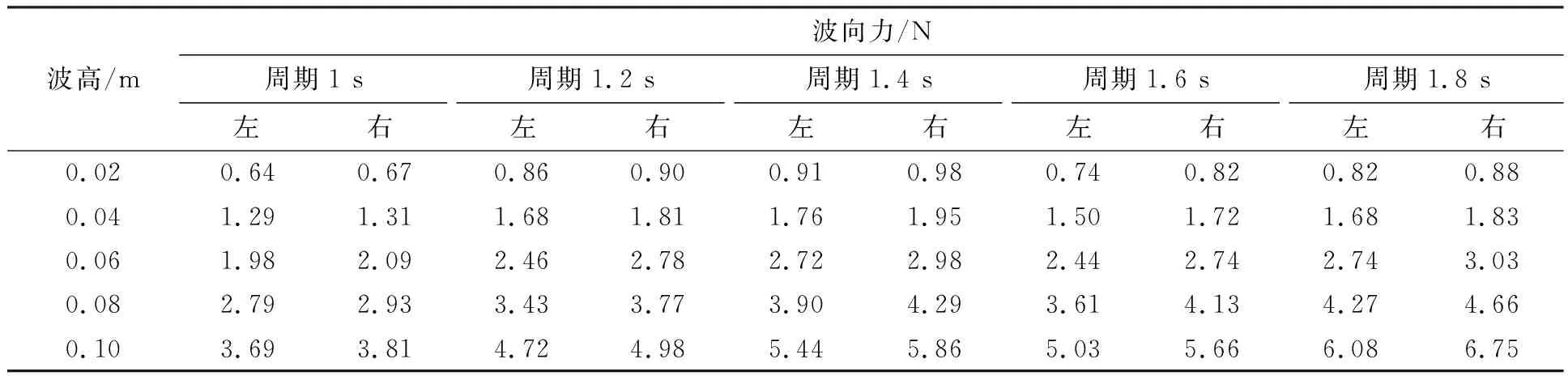
表2 不同波况下网箱受到的波向力最大值(吃水:左32 cm、右37 cm)Tab.2 The maximum wave direction force on the cage under different wave conditions(draft:32 cm on the left,37 cm on the right)

吃水32 cm和吃水37 cm两种工况下波向力的幅值与周期和预计波高存在着一定的联系,且在吃水37 cm时,波向力的幅值略大于吃水32 cm的情况。图3给出了网箱框架在吃水32 cm情况下不同波浪周期作用下受到的波向力幅值随波高的变化规律。

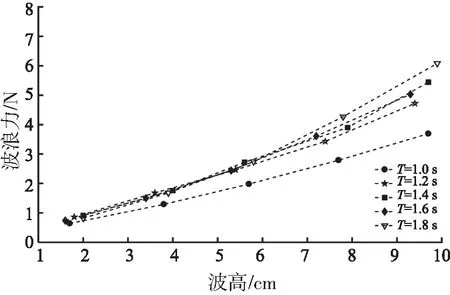
图3 网箱框架受力与波高和周期的关系Fig.3 Relationship between stress of cage frame and wave height and period

在同周期的情况下,网箱受到的波向力与波高存在着正相关的关系;而在波高一定的情况下,网箱受到的波向力和周期的相关性较小,从图中可看到除周期1 s情况外其他几种波浪周期在波高较小时并未有显著差别。在试验条件下,周期1 s的波浪波长为1.52 m,半波长与网箱的尺寸(网箱外接圆直径为0.9 m)相当,而在波浪周期为1.2～1.8 s时,网箱外接圆直径小于半波长,波浪周期为1 s时,波浪散射效应较其他情况相对比较明显,因此受力趋势差别显著。

为探究网箱受到的波向力成分以及波浪参数对波向力组分的影响,将波向力进行分离,分解为惯性力和阻力分量[35]:

F=FM+FD

(1)

(2)

式中:FM和FD分别为惯性力和阻力,kg·m/ s2;u为当地的水质点运动速度,m/ s;V为物体所占体积,m3;S为迎流面积,m2。阻力和惯性力的分离基于试验数据采用最小二乘法拟合得到。图 4给出了部分工况惯性力和阻力分离的结果(Fx表示网箱框架受到的波向力,Fd表示阻力,Fm表示惯性力)。不仅网箱受到的波向力大小与波高存在着相关性,分离出的阻力占比也与波高存在着相关性,在波高比较小的情况下阻力在波向力中占比较小,随着波高的增大阻力占比增加。

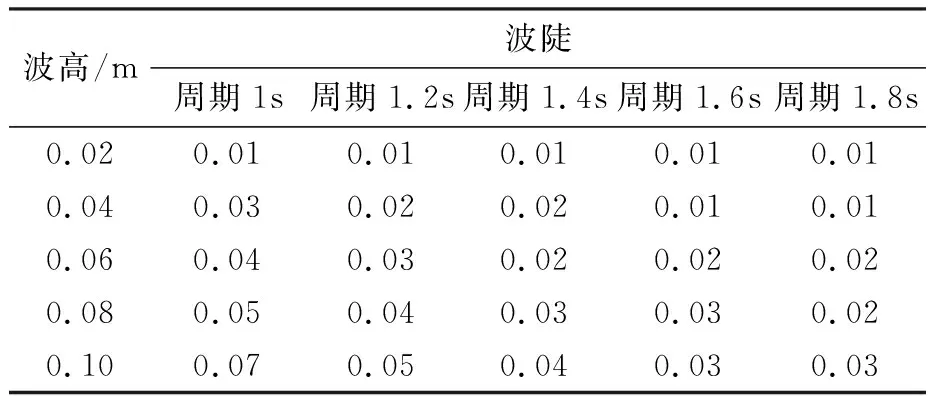
表3 试验工况波陡与波高、波长(周期)的关系Tab.3 Relationship between wave steepness,wave height and wavelength(period)under experimental conditions

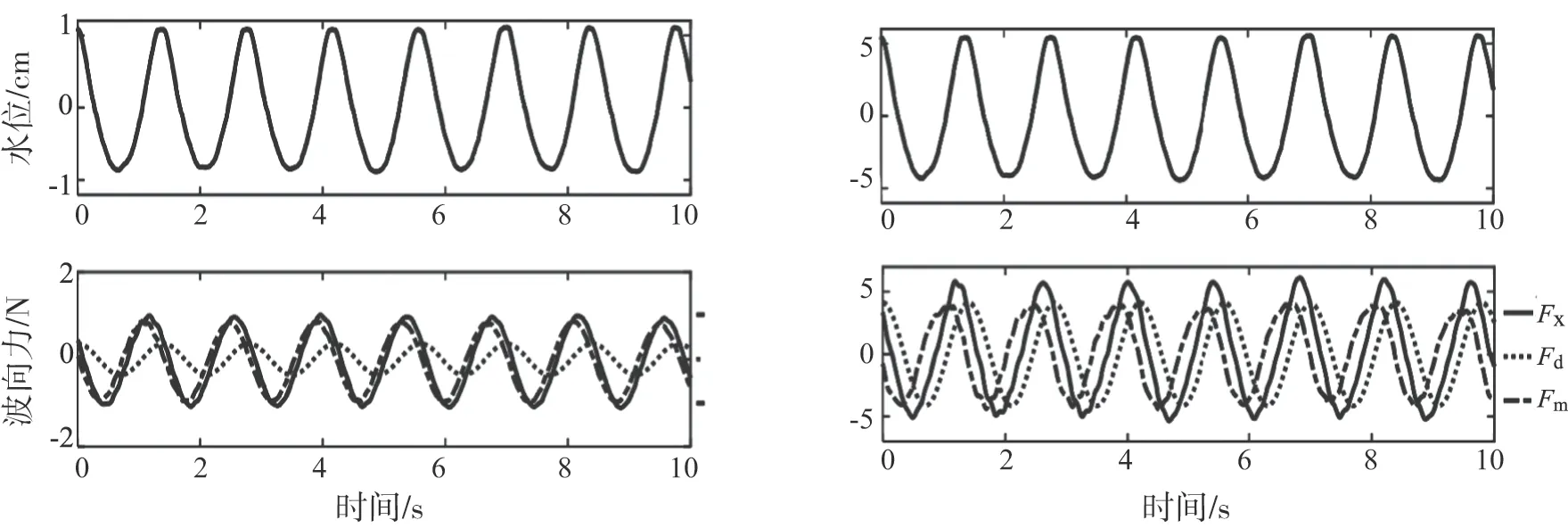
注:波浪周期1.4 s、波高2 cm(左)和波高10 cm(右)图4 网箱受到波向力时间过程线 Fig.4 Time series of longitudinal wave force with wave period

为了进一步分析网箱波向力特性,本研究基于傅立叶分析给出了不同波浪参数下波向力的频域特性。如图5所示,周期为1 s和1.8 s以及波高2 cm和10 cm波浪条件下波向力频域结果可以看到在波高较小时网箱受力非线性不明显,在波高较大的时候其受到的波向力有倍频的成分,且网箱所受波向力随着波陡增大倍频成分增加如图6所示。

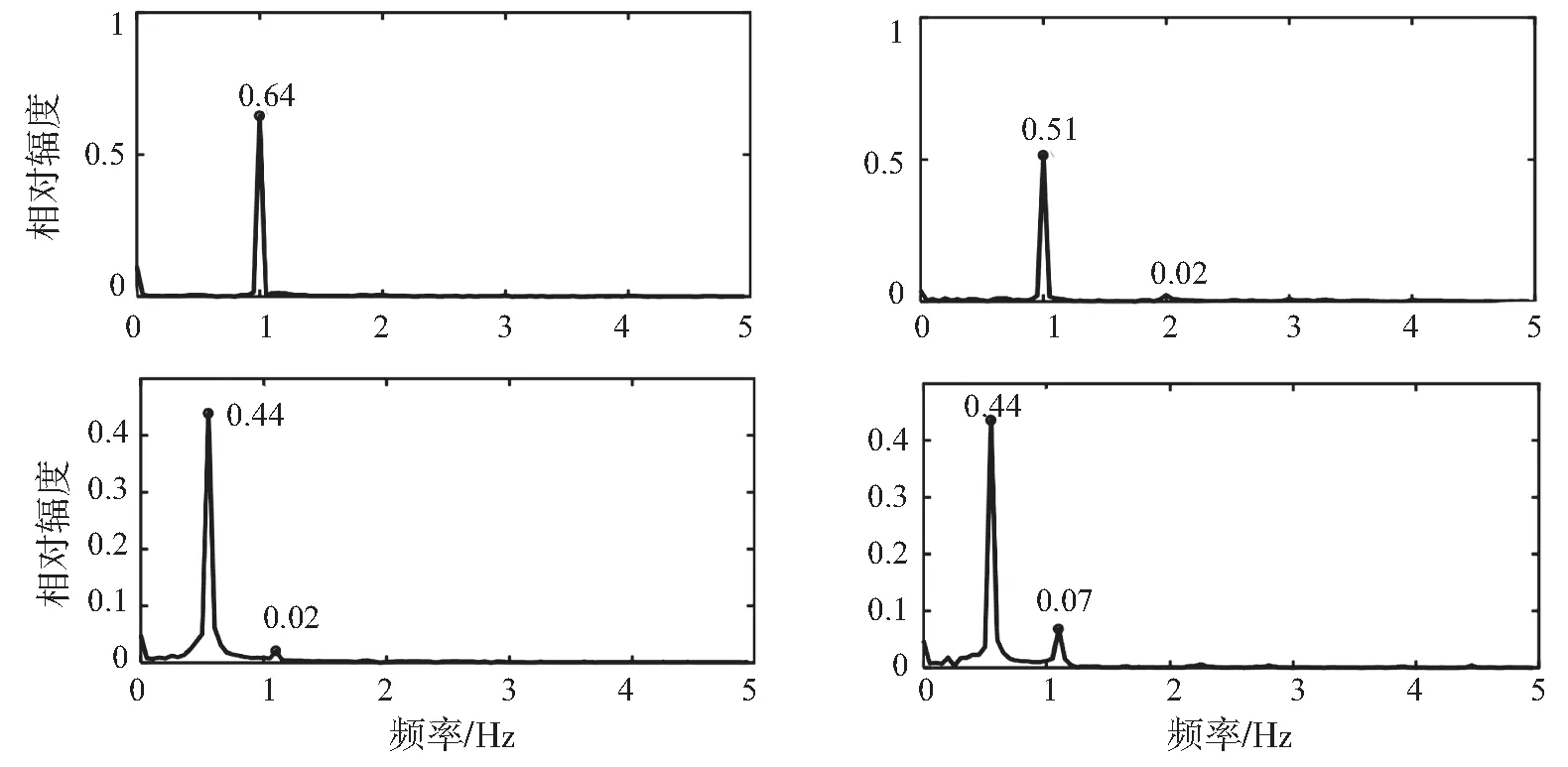
注:周期上1 s、下1.8 s;波高左2 cm、右10 cm图5 网箱框架在不同波高周期下受波向力的频谱Fig.5 Spectrum of wave direction force on cage frame under different wave height periods

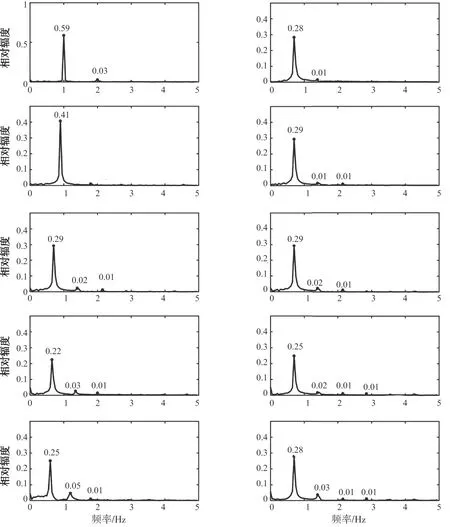
注:左波陡0.05周期1～1.8 s;右周期1.4 s波陡0.03～0.07图6 网箱在不同波陡与波周期下所受波向力的频谱Fig.6 Frequency spectrum of longitudinal wave force on cage under different wave steepness periods

2.2 网箱框架受力无量纲经验公式

为得到可以在工程实践中方便应用的经验公式。

(3)

(4)

(5)

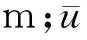
图7给出了网箱框架受力与KC数的变化关系,可以看到随着KC数的增大无量纲波向力变小且趋于常数。

图7 网箱框架受到的无量纲波向力与KC数关系Fig.7 Relationship between dimensionless longitudinal wave force on cage frame and KC number

引入当量直径作为特征尺度定义KC数,采用数据回归方法分析试验数据得到波向力与KC数的定量关系如式(6)。

(6)

2.3 带有网衣的网箱框架受力分析

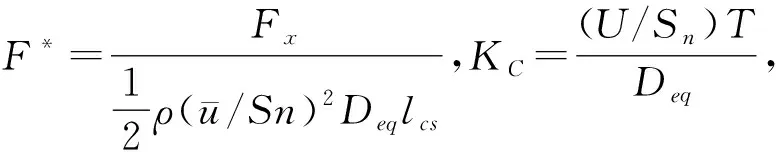
(7)

图8给出了有网衣情况下无量纲波向力随KC的变化规律并对试验数据进行了回归分析,分析发现将网衣阻水效应考虑进去后公式(6)仍适用。

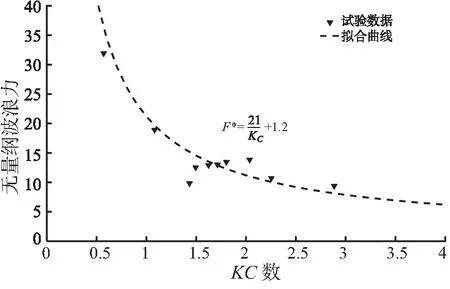
图8 有网衣情况下无量纲波向力与KC数的关系Fig.8 Relationship between dimensionless longitudinal wave force and KC number for the cage with net

3 数值分析

3.1 数值方法

水质点运动分解以及网箱框架模型如图9所示。

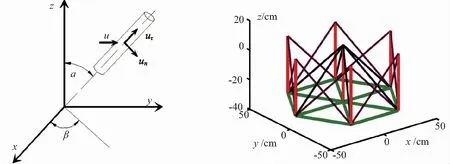
图9 水质点运动分解以及网箱框架模型Fig.9 Decomposition of water particle motion and numerical model of cage frame

根据波浪参数、杆件的直径以及其在波浪场中的位置,可以得到杆件的受力,沿杆长进行积分可得杆件的受力。由于Morison公式仅针对竖直杆件,其他方向杆件受力的计算首先要对当地水质点的速度进行分解。Morison公式也可以应用于倾斜的物体,计算方法是将未受扰动的速度和加速度分解到与圆柱轴相互垂直和平行的方向[36]。在阻力计算过程中将速度分解成垂直于杆件方向和沿杆件方向的两个速度矢量,杆件受到的阻力方向与水质点运动分解的法向速度方向同向。

在数值模拟中使用二阶斯托克斯波作为理论的波浪场。根据Morison公式(前文公式(1))中阻力系数CD和和惯性力系数CM受表面粗糙度和KC数的影响,根据大量的试验分析可以由下面关系式表示[37]:

CD=CDS(Δ)φ(KC)

(8)

(9)

(10)

式中:Δ=R/D,KC=uT/D,Cπ=1.5-0.024(12/CDS-0.65)。R为材料表面粗糙度,D为框架或者网衣线的特征长度。

(11)

3.2 数值结果分析

3.2.1 网箱框架的受力结果数值和试验的对比

如图10所示,在周期较小的时候,理论值比试验值略大,可能是由于波浪周期较小时,波长和网箱的尺寸比较接近,波浪散射效应较其他情况相对比较明显;在周期较大的时候数值结果和试验结果基本符合。

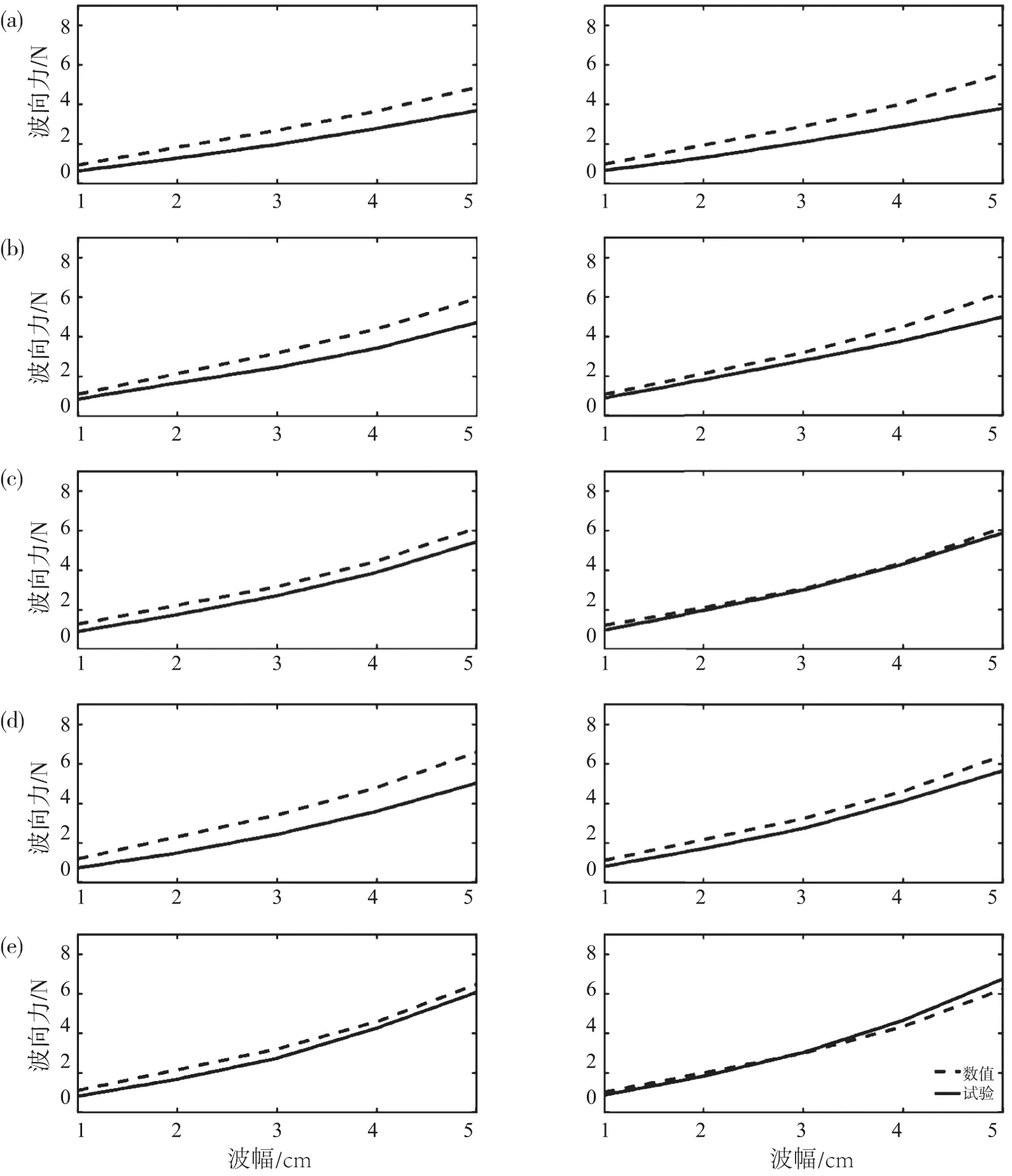
注:(a)～(e)分别对应周期1.0 s,1.2 s,1.4 s,1.6 s,1.8 s;左边和右边分别代表网箱吃水32 cm和吃水37 cm的情况图10 不同工况下数值计算结果与试验结果的幅值对比Fig.10 The comparisons of force amplitudes between numerical calculations and experimental results under different wave conditions

图11为数值结果和试验结果的受力对比。

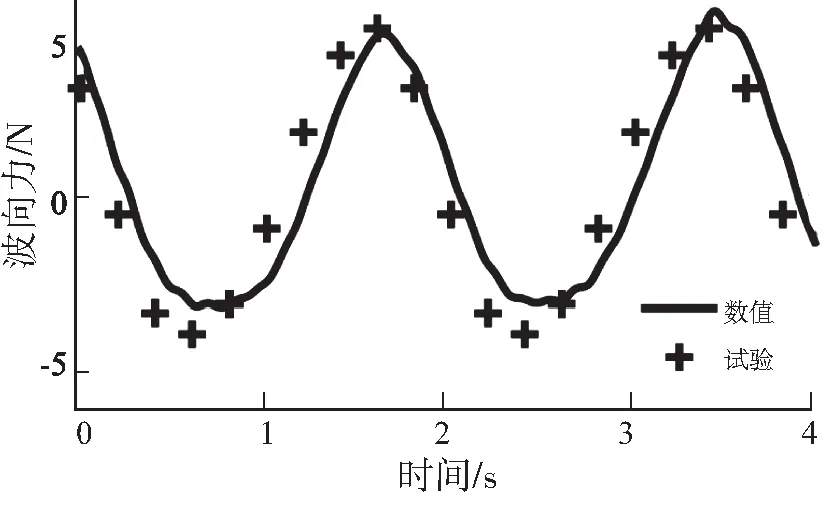
图11 数值结果和试验结果的受力对比Fig.11 Comparison of time series of longitudinal wave force between numerical results and experimental results

周期、时间线的形状和幅值大小都比较一致,振幅相对误差3.4%,峰值时间相对误差4.8%,在工程允许的误差15%之内[38]。相较于CFD计算方法[39],本研究的计算在相对误差满足工程实际的情况下,计算量较小,耗时较短。

3.2.2 带网衣的网箱数值计算结果

由于试验时所使用的网衣为刚性网,本计算不考虑柔性问题,假定网衣的网绳为细小圆柱,计算方式同上文中的网箱框架的计算方式,带网衣网箱框架的受力与试验的结果对比如图12所示。选取波浪周期为1.4 s,波高2～10 cm(波幅A为1～5 cm)的试验和理论计算进行对比。如图12所示,网衣的网箱框架受到的水动力试验和理论计算结果同样较为符合,不同波高下的最大误差5%,在工程允许的误差范围15%内[38]。证明了此计算方法不仅在网箱框架结构的计算中有效,在刚性网衣的计算中同样有效。

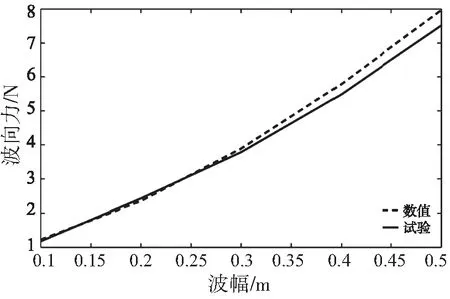
图12 带网衣的网箱波向力数值与试验结果对比Fig.12 Comparison of longitudinal wave force between numerical calculation and experiments with net

4 结论

开展了规则波作用下尺度缩比为1∶100的网箱模型水动力试验研究,研究表明网箱波向力随波高增加受力显著增加,傅立叶分析显示波浪的非线性与色散效应会增强波向力倍频特性。通过引入当量直径的概念,得到了此网箱在各种规则波工况下受力的经验公式,使用网衣孔隙率对网箱受力的经验公式进行修正,得到了满足网衣存在的情况下网箱波浪力的经验公式,得到了此类网箱快速计算的经验公式。为得到更一般的组合框架的计算方法,本研究基于Morison方程,根据不同结构位置的状况确定其阻力惯性力系数,对网箱框架和网衣进行数值计算。结果表明此方法不仅可以在网箱框架波浪力的计算中适用,在刚性网衣的存在下此计算方法同样适用,但是关于柔性网衣的适用性仍需进一步研究。