基于CFD的不同通风结构下渔船机舱通风系统性能分析

黄温赟,于得水,黄文超,朱陈程,赵新颖

(1 中国水产科学研究院渔业机械仪器研究所,农业农村部远洋渔船与装备重点实验室,上海 200092;2 青岛海洋科学与技术国家试点实验室,深蓝渔业工程联合实验室,山东 青岛 266237;3 国信中船(青岛)海洋科技有限公司,山东 青岛 266061)

机舱通风系统主要用于满足机舱内设备所需的温度、湿度和空气量等环境要素,保障设备良好运行[1],同时为轮机人员提供相对舒适的工作和卫生环境[2]。机舱通风系统设计是根据机舱内设备的需风量确定风机风量,并依据机舱内设备的布置确定风管走向和各风口的大小、型式等[3]。

ISO 8861—1998《造船 柴油船舶机舱通风设计要求和计算基准》[4]明确了机舱风量的计算方法,进而可以选择适宜的风机,但风管的布置直接影响着机舱内的通风效果。Heikkinen[5]简化了送风口模型,将多边形状的风口等效为有效送风面积相同的矩形风口,但该模型后被证实对非等温流体流动问题效果不理想[6]。梁彦超[7]采用计算流体力学(CFD)技术对某集装箱船的风口位置和大小进行了流场模拟和优化,优化了风口布置。赫伟建[8]应用Phoencis等软件模拟分析机舱内的通风系统,得出了机舱通风的速度场和温度场。周山[9]采用Fluent软件,用试验数据搭建出三维计算模型,进而优化通风效果。毕监龙[10]从船舶通风方式和系统布设难点出发,总结机舱通风系统船上布置注意事项,阐述机舱通风系统布置时的优化方案。国内大量学者关注于大型远洋货船的机舱通风系统[11],对于国内渔船等中小型船舶机舱内通风的数值模拟却缺少相关研究。在渔船机舱通风系统设计过程中,除了需要考虑冷冻机、消防设备、检测仪表等机械不同通风需求[12],还需要考虑机舱高度、风口位置、结构筋板、风管零部件等因素的影响,各送风口的风量差异较大,不均匀分布的状况突出[13-15]。

为准确模拟各风口的实际通风效果,提升渔船设计质量,以某远洋渔船为研究对象,基于计算流体力学方法[16]并运用STAR-CCM+软件对内部有加强筋的3种风管型式进行流体仿真,研究通风栅数量和加强筋高度等对风口流速的影响,为渔船机舱通风系统设计优化提供参考。

1 数值方法

1.1 控制方程

本研究数值模拟采用雷诺平均方程(N-S方程)[17],其笛卡尔坐标系下的张量表示为[18]:

(1)

(2)

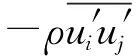
1.2 湍流模型

Spalart-Allmaras模型[20]是以涡黏性输运方程为核心的一次方程湍流模型,计算量小,对一定复杂的边界层问题有较好的效果[21-22]。具体湍流方程为:

(3)

公式右边分别为流动扩散项、涡粘产生项和湍流损耗项[23]。涡粘系数和涡粘产生项通过以下公式得到:

(4)

(5)

式中:d为积分点到物面的距离,Ω的模值为|Ω|,其余的辅助变量[24]的定义如下:

(6)

(7)

(8)

式中:cb1、cb2、cv1、cw1、cw2、cw3、σ,k为闭合常数,默认值[25]分别为cb1=0.1355,cb2=0.622,cv1=7.1,σ=2/3,cw1=(cb1/k2)+(1+cb2)/σ,cw2=0.3,cw3=2,k=0.41,cv2=0.7,cv3=0.9。

2 计算模型与边界条件

2.1 平台模型

渔船设有左右两侧风管,具体尺寸如图1所示。

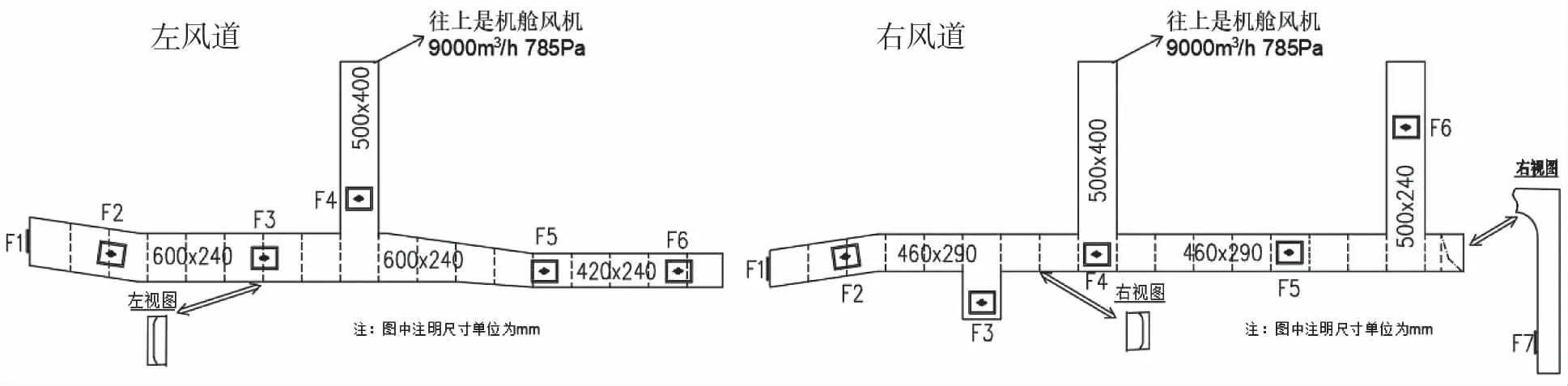
图1 左右两侧风管侧视图Fig.1 side view of left and right air ducts

其中箭头所指为加强筋。左侧风管布置一个进风口,6个可调通风栅F1～F6;右侧风管布置一个进风口,7个可调通风栅F1～F7。进风口尺寸均为500 mm×400 mm,可调通风栅尺寸均为240 mm×300 mm。模型简化按照以下原则开展:对管道内气流场产生较小影响的部件进行去除,着重考虑加强筋对气流的影响,对曲面作等面积平面化处理[26]。为研究加强筋对风道内流场的影响,本研究共设置3种风管型式进行比较:型式1,不对风管内的加强筋进行处理,每隔500 mm为一个高宽80 mm×10 mm的加强筋,共17个;型式2,在加强筋前后设置过渡,在风管上表面每隔500 mm设置一个边长为280 mm的正三棱柱,共16个;型式3,增设隔板隔开加强筋,形成标准矩形风管,即在风管上表面设置两个长宽高分别为3500 mm×600 mm×80 mm、4000 mm×600 mm×80 mm的长方体。左右两侧风管模型示意图如图2所示。

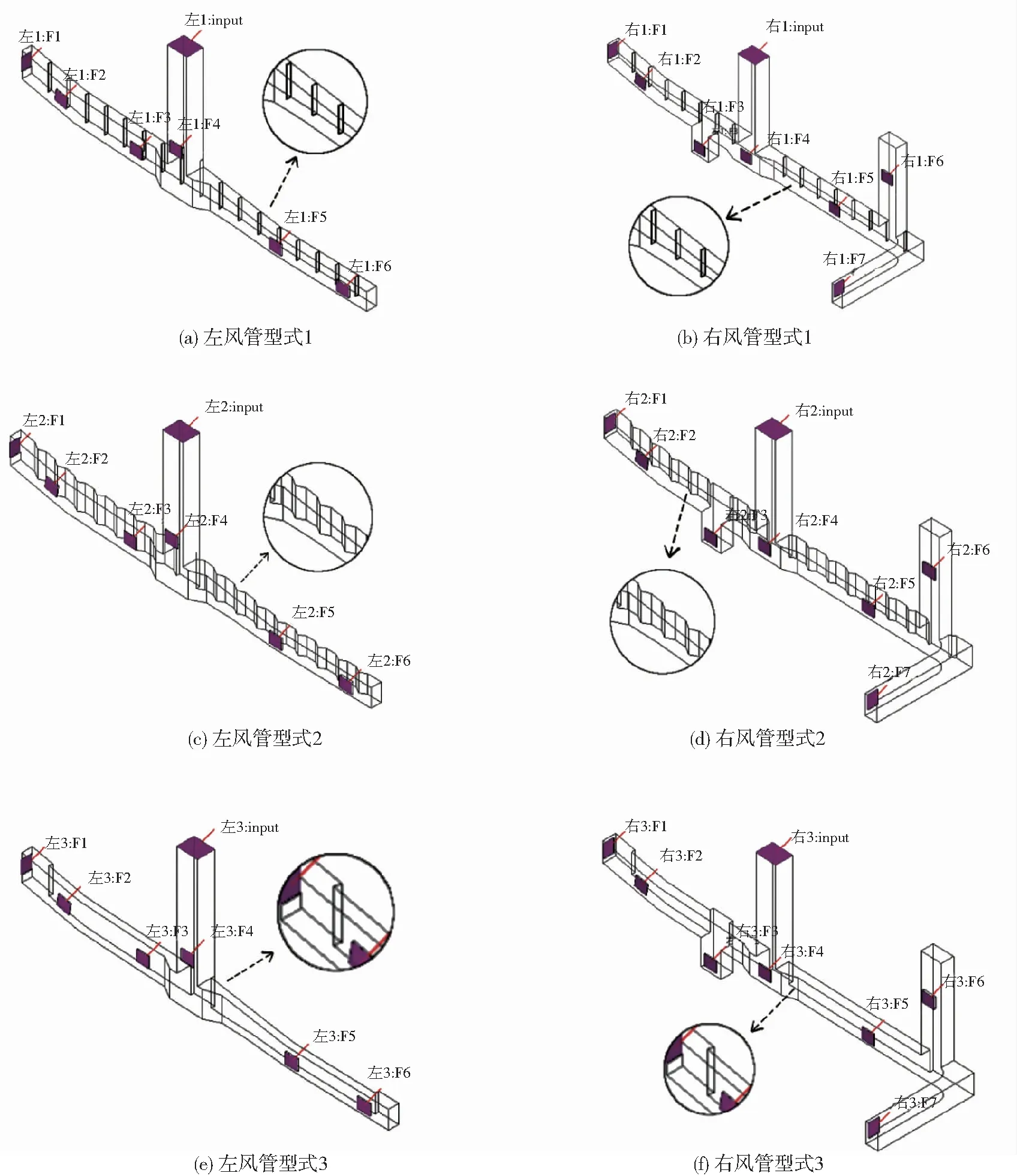
图2 左右两侧风管模型示意图Fig.2 Schematic diagram of left and right air duct models

2.2 计算网格划分

网格划分是CFD数值分析前处理中的重要部分,划分的质量将影响数值分析结果的精确性[27]。在划分网格时,全域采用六面体结构化网格[28]以保证数值模拟精度,平台壁面采用精细网格[29]并保证第一层网格位于黏性底层内。船舱风管的轮廓特征线进行线控制,同时对平台表面设置面控制,并做网格的光滑过渡,网格划分结果如表1所示。

左右两侧风管型式1的网格划分处理如图3所示,其他型式选用的网格单元尺寸相同。

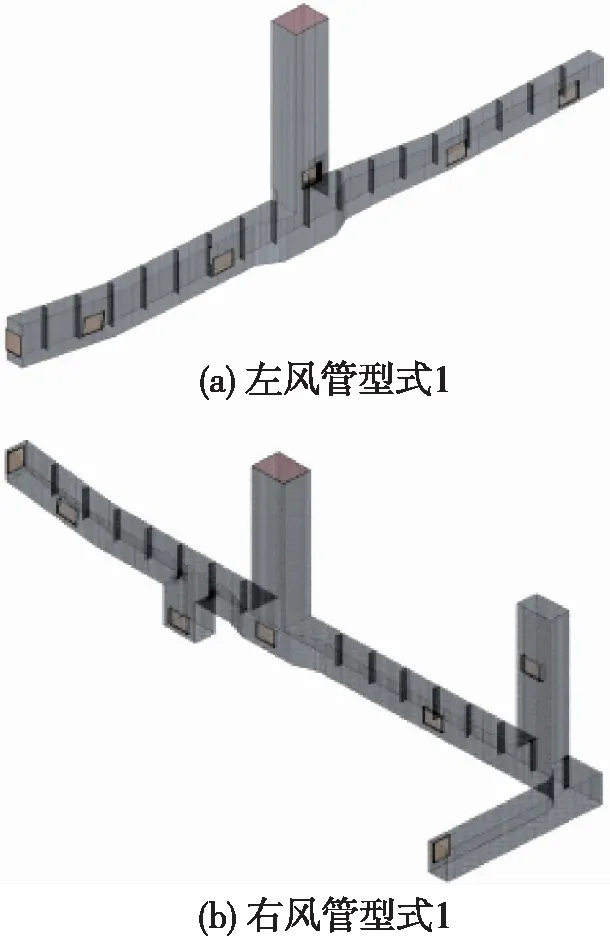
图3 风管网格划分Fig.3 grid division of air duct

2.3 边界条件的设定

进口边界条件:设定与机舱风机相连处为速度进口边界条件,速度设定为12.5 m/s,速度方向垂直于进口面向下。出口边界条件:设定出风口为压力出口边界条件。壁面边界条件:机舱风管内壁计算域内表面设置为无滑移壁面边界条件[30]。

3 模拟结果与分析

3.1 左右风管内流场和通风栅流速分析

风管内速度流线如图4所示。图4a～图4c为不同研究型式下左侧风管内的速度流线图。保持进口速度12.5 m/s不变,观察3组型式下风的流线对比可得:距离速度入口越近,速度流线越密集;型式1的速度最大值较大,型式2其次,型式3速度最大值最小;型式1风管的流线最为复杂且在通风栅F6右侧形成了一个较明显的涡流,型式2的速度流线较为流畅且通风栅F6右侧无涡流,型式3的速度流线最为流畅,涡流最少。

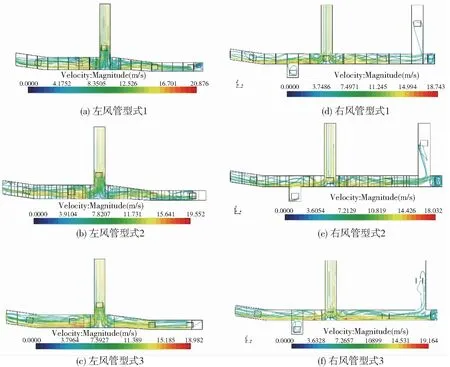
图4 风管内速度流线图Fig.4 Velocity flow diagram in duct

图4d～图4f为不同研究型式下右侧风管内的速度流线图。保持入口速度12.5 m/s不变,观察3组型式下风的流线对比可得:距离速度入口越近,速度流线越密集;通风栅F3和通风栅F6处的流线最为稀疏,说明直角支管内风量较小;三组型式下通风栅F7支管段涡流较多,与该处风道直角有关;型式1下通风栅F4附近形成一处涡流,而型式2和型式3却没有,这与风管内加强筋隔档有关;型式3的速度流线最为流畅,局部流速较高,这是由于风管内表面平滑,而截面积相比其他两型式小,因此流速较高。左右风管各通风栅速度如图5所示。

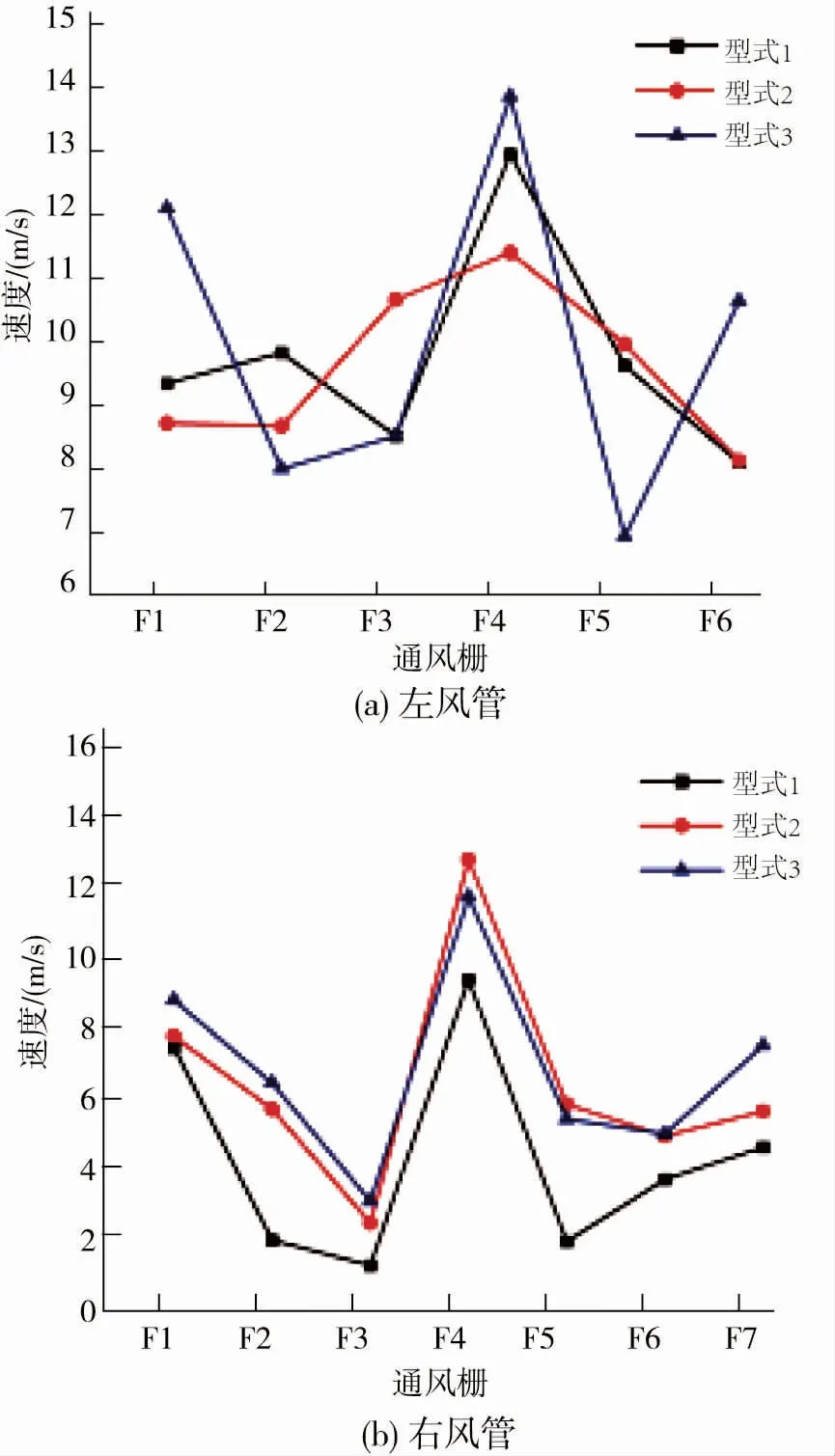
图5 左右风管各通风栅速度Fig.5 Velocity of each gate of the left &right duct

图5a为左风管各通风栅速度分布。进口速度设置为12.5 m/s,3种型式下通风栅风速最大值均为主风道上近支管处的通风栅F4,风速分别为12.98 m/s、11.45 m/s、13.87 m/s;型式1和型式2下通风栅风速最小值均为末端的通风栅F6,速度大小为8.23 m/s;型式3下通风栅风速最小值为风管平直段的通风栅F5,速度大小为7.06 m/s,通风栅F2和F3风速也相对较低。对比可得,相比型式1和型式2,型式3末端通风栅风速明显加大,但风管平直段处的通风栅风速相对偏小,各通风栅风速差别很大;型式2中的各通风栅风速差别较小。

图5b为右风管各通风栅速度分布,进口速度设置为12.5 m/s,3种型式下通风栅风速最大值均为主风道支管处的通风栅F4,风速分别为9.96 m/s、13.31 m/s、12.28 m/s;三种型式下通风栅风速最小值均为支管上的通风栅F3,风速分别为2.06 m/s、3.18 m/s、2.79 m/s。对比可得,3种型式下各通风栅的速度分布规律相似,但型式1各通风栅风速明显低于其他两型式;同为支管上的通风栅,F5的风速比F3要大;风管端口处的通风栅风速相比方管平直段上通风栅的风速要大。

3.2 不同通风栅数量下风速分析

针对机舱右侧风管部分通风栅的速度较小,通过关闭部分通风栅以研究不同通风栅数量下风管速度,各工况设定如表2所示。

表2 工况设定Tab.2 Setting of working conditions

图6为3种型式下不关闭通风栅、关闭通风栅F4和关闭通风栅F1及F4的速度对比。

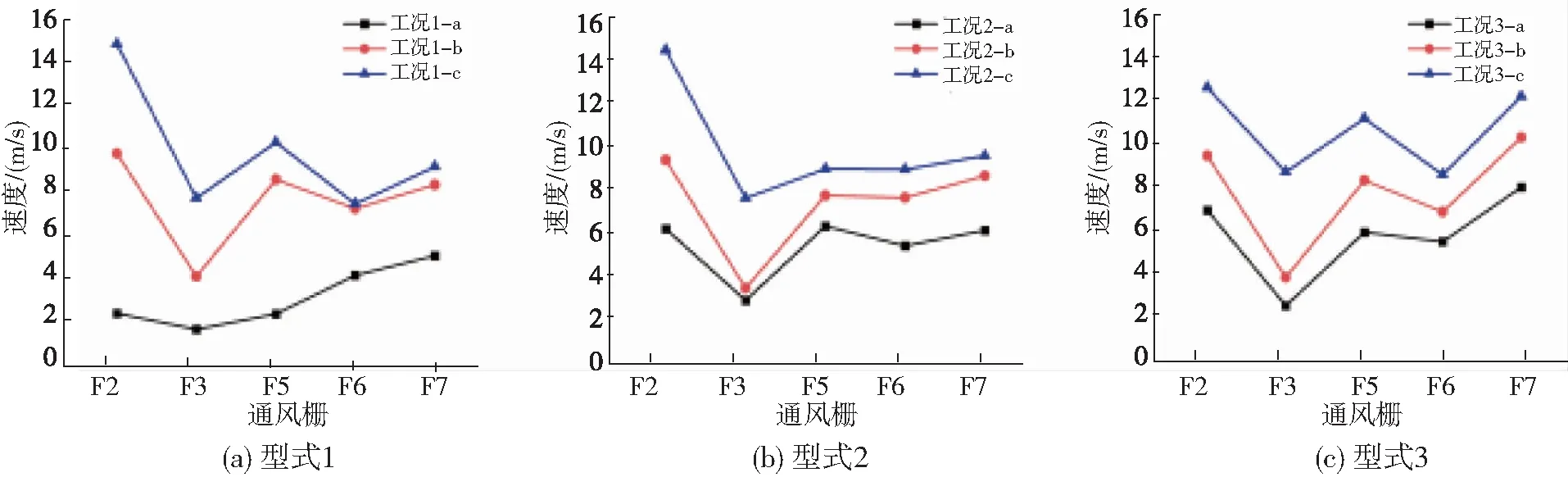
图6 右风管关闭F1、F4通风栅速度分布Fig.6 Velocity distribution of ventilation gate F1 and F4 closed by right air duct

关闭通风栅F4后,3种型式的各通风栅速度变化较大,通风栅风速平均值均增加到8.47 m/s、8.25 m/s、8.56 m/s,增长率分别为102.1%、36.3%和30.7%,型式1的通风栅速度变化最大;3种型式下通风栅风速最小值仍为通风栅F3,风速分别为4.36 m/s、3.73 m/s、4.07 m/s。

关闭通风栅F1及F4后,3种型式下通风栅风速最大值均为通风栅F2,风速分别为14.73 m/s、14.32 m/s、12.62 m/s;3种型式下通风栅风速平均值均增加到9.95 m/s、9.94 m/s、10.98 m/s,与不关闭通风栅相比增长率分别为137.1%、64.4%和64.1%;与不关闭通风栅和仅关闭F4通风栅相比,各型式的通风栅风速增加趋势类似。

3.3 不同加强筋高度下风速分析

针对不同加强筋高度对通风栅风速的影响,基于左右风管的3种型式对60 mm、70 mm、80 mm、90 mm、100 mm高的加强筋下的计算域进行数值模拟分析。

图7为左侧风管速度分布图,3种型式下通风栅F4的风速随着加强筋高度的增加而增加。由图9a可知,型式1两端的通风栅F1和F6风速随着加强筋高度的增加而震荡下跌,平直段通风栅F2和F5风速随着加强筋高度的增加而增加;由于位置原因,通风栅F2的风速在强筋高度为80 mm时最大。由图9b可知,型式2通风栅F1的风速随着加强筋高度的增加而减小,通风栅F3的风速随着加强筋高度的增加而增加,加强筋高度对通风栅F5和F6的风速影响较小。由图7c可知,型式3通风栅F1和F3的风速在强筋高度为80 mm时最大;加强筋高度对通风栅F2、F5和F6的风速影响较小。

图8为右侧风管速度分布图。由图8a可知,型式1除通风栅F6外,其余通风栅的出风速度在强筋高度为80 mm时最小;通风栅F2和通风栅F5的出风速度随加强筋高度的变化规律相似,加强筋高度对通风栅F1和F6的出风速度影响较小。由图8b可知,型式2通风栅F3、F4和F5的出风速度随着加强筋高度的增加而增加;通风栅F7的出风速度随着加强筋高度的增加而减小;加强筋高度对通风栅F1和F6的出风速度影响较小。由图8c可知,型式3通风栅F2的出风速度在强筋高度为80 mm时最大;除通风栅F2外,加强筋高度对其余通风栅的出风速度影响较小。

4 结论

通过对比研究3种不同风管型式下通风栅的风速,分析了通风栅数量及位置和加强筋高度的不同对各通风栅处风速的影响,得出以下结论:距离速度入口越近处速度流线越密集,风速越大;内表面平滑的风管流态最流畅,风道两端通风栅风速较高,直管段上的通风栅出口风速较小,直角支管内流速较小。关闭风管入口和风管端口处的通风栅对其他通风栅出口风速影响明显,可考虑该处采用可调型式通风栅,用以平衡其他通风栅的出风量;直管段处的通风栅可考虑增加导流板以加大出风量。加强筋高度上的增加总体上会引起风道各通风栅的风速更加不均衡,流场更加紊乱,不利于各出风口风速均衡。

为了纯粹讨论气体流场,在模型简化上忽略机舱中管系及冷却器等小型设备对气流的影响,并将其散热简化为均匀分布在壁面上的热流量,未来将进一步考虑机舱内部温度场对通风的影响,并开展模型试验,验证数值模型的有效性,为中小型渔船通风设计提供指导。