基于机器视觉技术的金鲳鱼质量预测研究
单佳楠,郑晓伟
(1 上海海洋大学工程学院,上海 201306;2 中国水产科学研究院渔业机械仪器研究所,上海 200092)
近年来,随着金鲳鱼(Trachinotusovatus)人工育苗与深水网箱养殖两大关键技术的突破,推动了金鲳鱼产业的蓬勃发展。早在2016年,金鲳鱼就已成为国内五大海水养殖鱼类之一,2020年中国金鲳鱼年总产量达18万t[1]。金鲳鱼主要的加工产品种类有冻品、冰鲜以及少量的活鲜鱼,前处理加工需按照不同的质量进行分级。目前,金鲳鱼分级主要依赖人工称重分级,这种分级方法效率低,且分选受人工主观因素影响易产生误差,难以满足快速生产的要求。随着计算机技术的发展,机器视觉技术也越来越多地应用到自动化行业当中[2],如物流、金属加工、食品加工等。机器视觉技术不仅可以提高生产效率,还能提升产品质量[3],能够无接触、无干扰地获取所需信息、并且在人眼无法达到的环境中应用。机器视觉技术代替人眼是未来发展的必然趋势,国内外已有相关研究将机器视觉技术应用到生产加工当中,如多种淡水鱼分类[4]、梭子蟹质量估计[5]、鱼新鲜度检测[6]、大黄鱼弧菌病监测[7]等。
本研究利用机器视觉技术对金鲳鱼图像进行采集、预处理后,对预处理后图像的有效特征逐一计算分析,建立多个金鲳鱼质量预测模型,通过分析对比,选取预测误差最小的预测模型,为后续金鲳鱼自动化质量分级加工提供理论依据。
1 材料与方法
1.1 研究材料
本研究共购入产自海南昌江棋子湾深海海域的养殖冷冻金鲳鱼100条,在解冻和去除表面水分后对其逐一称重,测得其规格区间为302.3~507.8 g,并对每条金鲳进行编号,其中80条将作为本次研究的建模样本,其余20条作为预测模型的检验样本。
1.2 研究方案
为获取金鲳鱼图像的特征参数,需构建金鲳鱼图像采集系统。该系统由硬件和软件两个部分组成,硬件部分主要包含摄像头固定支架、LED光源、遮光棚、纯色背景布、视觉相机、树莓派计算机等[8]。研究方法流程如图1所示。

图1 研究方法流程图Fig.1 Research method flow chart
软件部分主要包含Python 3.9与OpenCV库,建模过程主要使用Excel与SPSS软件。采集过程相机始终为固定高度,便于后期标定。相机分辨率为1 920×1 080,230万有效像素,采用USB3.0传输数据。树莓派计算机采用Linux开源系统,该系统简洁易上手,非常适合开发。预试验中依据图像直方图对不同背景颜色的轮廓提取效果进行对比,结果显示绿色背景布对于金鲳鱼轮廓识别效果更好。本试验主要使用Python语言进行编程,程序主要包含图像采集与预处理,图像特征提取两个模块[9]。
1.3 图像采集系统
由于金鲳鱼体态扁平,且质量主要分布在鱼体中心部位,鱼体厚度区分较小,因此采用投影图像作为特征图像,建立金鲳鱼投影图像特征和金鲳鱼质量之间的关系。研究共采集100条金鲳鱼图像,2个长条形LED灯固定在遮光棚顶部,使用相机在遮光棚下静态拍摄金鲳鱼,采集金鲳鱼的镜头到平面的距离均为35 cm,相机通过USB3.0与树莓派计算机连接,拍摄后编号保存。图像采集装置示意图及实物图如图2所示。
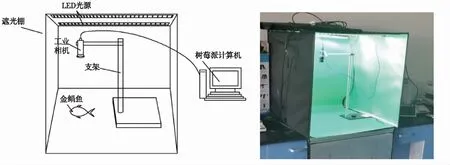
图2 图像采集装置示意图及实物图Fig.2 Schematic diagram and physical map of the image acquisition device
1.4 图像处理
1.4.1 图像去噪
为减少图像噪声,将原图像进行高斯滤波处理,高斯滤波去噪就是对整幅图像像素值进行加权平均,针对每一个像素点的值,都由其本身值和邻域内的其他像素值经过加权平均后得到[10]。
本试验采用高斯滤波核为5×5,经高斯消噪后的图像如图3所示。

图3 高斯滤波后的金鲳鱼图像Fig.3 Image of golden pomfret after gaussian filtering
1.4.2 阈值处理
阈值处理是通过去除图像中像素值超出某一阈值或低于某一阈值的像素点[11]。其函数表达式为:

(1)
依据获取的图像直方图和多次阈值分割尝试,确定阈值maxVal为5分割效果较好,得到二值图像,实现背景和前景的有效分离[12]。由于后续图像特征处理需要基于二值化图像,因此对灰度化后的图像二值化处理。去除背景后图像直方图与未去除前图像对比如图4所示。
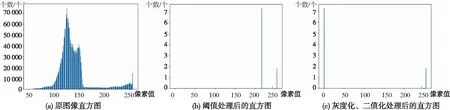
图4 图像直方图Fig.4 Image histogram
1.4.3 图像灰度与二值化处理
在灰度图像中像素的颜色值被称为灰度,也指黑白图像中像素点的颜色深浅程度,点值的范围从 0到255取整数,黑色为0,白色为255[13]。图像灰度化是图像预处理的重要步骤,可为后续图像分割、识别与分析等操作服务。图像灰度化处理有以下几种方式:分量法、最大值法、平均值法、加权平均法[14]。
本次试验采用加权平均法,将3个分量以不同的权值进行加权平均。由于人眼对绿色的敏感最高,对蓝色敏感最低,对RGB三分量进行加权平均能得到较合理的灰度图像。研究采用常用的经验公式也被称为心理学灰度公式[15]。
Gray=0.114B+0.587G+0.299R
(2)
在二值图像中添加一些位于黑色与白色之间的颜色深度,就构成了灰度图像。从最暗的黑色到最亮的白色可分为多个灰度级[16],当灰度级最低时便是二值图像。
图5所示为其于灰度化处理后的金鲳鱼图像。

图5 灰度化处理后的金鲳鱼图像Fig.5 Image after grayscale processing
二值图像的本质是只存在黑、白两种颜色的图像,而且像素仅有0、255两种取值,其中0表示黑色,255表示白色。
图6所示为基于不同maxVal值时的图像。

图6 不同阈值时的二值图像Fig.6 Binary diagram of different thresholds
由图6可得阈值为170时,无法准确分离前景与背景,当阈值为200时能较好地区分前景与背景,且比阈值为230时显示更多的轮廓细节。依据公式(2)和多次试验,得出设置阈值maxVal为200图像处理效果最好。二值化处理后得到的金鲳鱼图像如图7所示。

图7 二值化处理后的图像Fig.7 Image after binarization
1.4.4 形态学去噪
从二值处理后的图像中观察到,在图像轮廓周围存在白色干扰点。因此对图像进行形态学操作来过滤图像中存在的干扰点。形态学操作包含:腐蚀、膨胀、开运算、闭运算、梯度运算、黑帽运算、礼帽运算等操作[17]。
腐蚀操作能把位于图像边缘的像素点去除,使图像沿轮廓边缘向内收缩[18],也能消除小于特定大小的结构。腐蚀操作能使二值图像中的前景轮廓更加明朗,从而实现消除噪声、要素分割等功能。在腐蚀操作中,一般使用单个结构元(kernel)来逐一像素地遍历将被腐蚀的图像,并通过结构元与被腐蚀图像的关系来确定处理结果[19]。腐蚀与膨胀操作都是逐个像素地来决定像素值,每次判定的点均为和结构元中心点对应的点[20]。
开、闭运算融合了前面两种方法,在运算顺序上有些不同。开运算操作是先将图像腐蚀操作,再对腐蚀后的图像进行膨胀[19]。因此,开运算可以实现去噪、计数等功能。闭运算首先进行的是膨胀运算,再进行腐蚀运算[21]。结合本次金鲳鱼灰度图像的特点和需求,基于上述原理本研究对金鲳鱼二值像进行开运算操作,经过对比得出当结构元kernel=15时,既能保留原始图像的轮廓特点,又能准确去除图像周边噪点。
如图8所示,当开运算的kernel较小时,边缘会产生影响结果的边缘“气泡”,当kernel=15时,轮廓细节得到了较好的保留,并且消除了“气泡”,当kernel=20时,从图像中看到图像锯齿状更加明显,且轮廓细节丢失较多。

图8 kernel值不同时的边缘轮廓图Fig.8 Edge contour diagram with different kernel values
此外对于轮廓拟合曲线的选定不同kernel值也会有所影响,结果如图9所示。综上所述,因此形态学操作的kernel值选取为15。

图9 kernel值不同时轮廓的拟合直线图Fig.9 Fitting line graph of contour with different kernel values
1.5 特征提取
特征提取包含图像面积、周长、长短轴、去鱼鳍后图像面积等参数,人工测量特征包括含鱼鳍体宽与体长、不含鱼鳍体宽与体长、鱼眼直径、头鳍宽、鱼尾部最窄处宽。
由于特征参数均由图片信息获取,所得的参数单位都以像素为单位,因此需要获取实际物理尺寸和像素之间的换算关系,通过图像标定的方法,建立相机成像的几何模型[22]。

对标定图像在相同条件下摆放位置不同的同一黑色正方形块拍摄了3张图像。
已知拍摄图像为50 mm×50 mm的正方形,为减小误差,对三张图的计算结果取平均值,结果如表1所示,得到像素面积平均值为43 308.5,像素周长平均值为846.48,依据公式,可得比例系数ε1=846.48/200≈4.23,ε2=43 308.5/2 500=17.32。最终换算成实际尺寸数据部分如表2所示。

表1 图像标定面积和周长测量表Tab.1 Image calibration area and perimeter measurement scale

表2 样本数据平均值Tab.2 Average value of sample data
为了减小由于鱼体轮廓边缘阴影,鱼体摆放并未完全水平等因素造成的投影面积误差,研究对同一鱼体背面和正面图像均做了特征提取,并将平均值作为建模数据样本。
2 结果与讨论
2.1 预测模型建立
鱼体参数与质量相关系数如表3所示。

表3 鱼体参数与质量相关系数Tab.3 Correlation coefficient between body parameters and weight
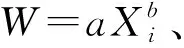
决定系数R2计算方式如式(3)所示。
(3)

金鲳鱼质量预测模型如表4所示。
2.2 模型建立结果
基于80组已记录的数据,利用SPSS软件建立了如表5所示的质量预测模型。

表5 金鲳鱼质量预测模型Tab.5 Weight prediction model of golden promfret
由于金鲳鱼质量和图像面积之间存在较强的相关性,通过对模型分析,发现金鲳鱼质量和图像面积之间的膨胀因子VIF值大于10,因子间存在严重共线性,因此采用主成分分析法进行一元线性建模,其中主成分公式:
X=0.288S*+0.279L*+0.259D*+0.257d*
(4)
式中:上标*表示Z标准化后的数据[26]。
主成分一元线性建模的决定系数R2为0.875,线性建模方法无法很好地拟合质量预测曲线,因此考虑主成分曲线回归的方法建模。由表6可得,主成分曲线回归中二次和三次模型R2较高,为0.877,其中二次曲线回归具有最小的标准估计的误差,但对于模型拟合效果提升程度不大。

表6 主成分曲线模型Tab.6 Principal component curve model
试验采集了样本的鱼鳍质量、去除鱼鳍后的金鲳鱼鱼体面积,并且计算了鱼鳍质量占比α1和去鱼鳍后图像投影面积占比α2。建立以α1、α2、S为因子的线性回归模型,该模型绝对决定系数R2达到了0.919。该模型因子间不存在明显共线性,因此该模型可用于质量预测,得到质量预测模型方程:
W=27.287α1×100+0.825α2×100+0.001456S-239.244
(5)
2.3 预测模型验证与讨论
利用一组20条金鲳鱼检验样本进行模型验证,鱼体质量预测值部分大于实际值。验证结果如图10所示。
预测结果平均相对误差2.73%,优化后平均相对误差为2.43%。平均绝对误差10.81 g,优化后平均绝对误差为9.62 g。均方根误差RMSE为14.22 g,优化后均方根误差RMSE为12.78 g。优化后的模型预测值和真实值线性回归曲线,决定系数R2为0.944,高于优化前模型的决定系数(0.930)。
2.3.1 鱼鳍面积对模型的影响
去鱼鳍前后投影图像如图11所示。有研究表明[28],由于鱼体各部位密度不同,对鱼体各部位投影面积进行校正可提高模型预测精度。金鲳鱼鱼鳍成薄片状,由图11可知,鱼鳍(含腹背鳍、尾鳍)占总面积比率较大,单位面积质量小。
依据试验测量数据得:去鱼鳍后面积占比最大值为85.41%,最小值为81.72%,平均值为83.3%。总体上,鱼鳍面积随鱼个体增大而增大,去鱼鳍后面积占比呈现相对稳定的趋势。但去鱼鳍后的图像投影面积是采用后处理手段获取的参数,图像实时处理无法直接获取,因此将80组数据去鱼鳍后图像投影面积占比取平均值,式(5)中α2取平均值作为预测模型方程常数项。
2.3.2 鱼鳍质量对模型的影响
张志强等[29]的研究显示鱼体质量与鱼体各部位区域质量具有较大关联,通过鱼体各部位质量比率对投影面积调整提升模型预测效果。华元渝[30]采用了多种方法建立鱼体长、体周长、体高与鱼质量间关系。由于鱼腹背鳍、鱼尾鳍占鱼体质量较小,但在投影面积中占比较大。因此考虑计算金鲳鱼鱼鳍质量占总质量的比率因素对模型的影响。依据测量数据得:鱼鳍质量占总质量最大值为1.40%,最小值为1.01%,平均值为1.21%。鱼鳍质量随鱼体质量增大而增大,呈线性相关趋势,鱼鳍质量占比变化趋于稳定。因此式(5)中α1可选取平均数作为常数项。
2.3.3 试验误差对模型的影响
由试验结果可知,预测模型能够实现对金鲳鱼质量的预测,但仍存在一定误差,通过对试验环节进行分析,可能存在以下问题:一是受试验客观条件限制,获取图像的背景存在水渍或污染,影响图像的分割及参数值;二是试验材料的影响,可能存在鱼的批次不同,造成鱼体个体形态有轻微差异,另外鱼体实际质量称重时只去除了鱼体表面水分,鱼体内水分含量存在个体差异,引起参数结果误差;三是提出的预测模型数量有限,样本数量有限,这些试验误差会对模型预测精度产生影响。为了提高模型精度,可以在提高精度的情况下增加样本数量或建立更为复杂的预测模型。
3 结论
采用鱼体投影图像参数建立质量预测模型研究较多,但研究都未指出鱼体正反投影图像处理结果存在计算误差。本研究针对采集的金鲳鱼图像,将其正反投影图像参数取平均值,作为建模所需的因子,以此减小正反投影图像差异对模型的影响。金鲳鱼鱼鳍面积、鱼鳍质量与鱼体质量呈线性相关,但鱼鳍质量占比α1、去鱼鳍面积占比α2在较小范围内变化。因此本研究通过α1、α2对模型进行校正。结果表明,基于图像面积S、鱼鳍质量占比α1、去鱼鳍面积占比α2的线性回归模型具有较高的预测精度和较小的标准估计误差,模型的决定系数为0.919,优于主成分回归方法与一元线性回归法。回归模型预测值与真实值决定系数R2为0.944,平均相对误差为2.43%,标准差为2.32%。由试验结果知,通过本研究建立的金鲳鱼质量预测模型能够在无接触的情况下预测出金鲳鱼的质量,为后续金鲳鱼自动化质量分级提供服务。

