基于Black-Sholes 期权模型的可转债定价与交易策略

李在侨（副教授） （广东科技学院财经学院 广东东莞 523083）

一、引言

随着全球经济的不断发展，我国的金融市场也在不断完善和进步，在诸多的金融衍生工具中，可转换债券日益受到人们的广泛关注。世界上第一支可转换债券于19 世纪40 年代在美国纽约正式发行，此后可转换债券在西方的资本市场上进入快速发展阶段。与西方国家相比，我国可转换债券的发展较为滞后。1992 年，我国首支可转换债券由宝安集团发行，揭开了我国可转债市场发展的序幕；2007 年“再融资新法规”发布，政策上的优势给予了可转债蓬勃发展的空间；2010 年，中国银行和中国工商银行发行可转换债券，意味着我国可转换债券市场发展进入一个新的阶段。近年来，随着我国经济发展水平的不断提升，可转换债券市场也在不断地发展和进步，融资规模不断扩大。

与股票市场和债券市场相比，我国的可转换债券市场，无论是从深度上还是从宽度上，都存在较大差异，但由于可转换债券自身具有的特点是其他金融工具所无法替代的，特别是可转换债券具有的资本转换性质，使债券持有人和发行公司可根据股票的市场价格约定较高的转股价格进行交易，从而最大限度实现自身利益保护的目的。因此，可转换债券的定价交易策略成为近年来国内学者关注的热点。然而，国内目前尚未研究出适合我国可转换债券市场的研究工具，相关研究主要是在借鉴西方理论基础上进行的，因国情、政策和体制等存在一定的差异，西方理论并不完全适合我国的可转换债券市场。本文以我国上市公司中具有代表性的10 家发行可转债的企业作为研究对象，进行深入分析、探索，以总结出适用我国的可转债交易策略。

二、文献综述

（一）国外文献综述

在19 世纪初，国外就有学者开始从事对可转换债券定价和交易的研究，国外学者关于可转换债券定价和交易的很多研究理论有较高的参考价值。Weinstein（1931）研究了转股期的可转债，分析转股权成效后权证和套利产生机理，最后因技术和理论水平有限，没有运用到模型中去。Ingersoll（1977）认为回购的可转债的理论价值是不能回购的可转债价值与回购权的价值总和。Brennan 和Schwartz（1980）将影响利率变化的因素纳入可转换债券的价格模型，事实上，可转债的价格与随机利率的变动基本无关。Cheung 和Nelken（1994）使用二叉树价格模型，计算了可转债的理论价格，在模型中主要考虑了正股价和无风险利率两个因素。Nick Calamos（2004）总结了在实践中被广泛认为代表可转换债券价格和条件的政府债券价格理论。Aann等（2008）通过蒙特卡罗模拟确定了美国32种可转让、可兑换债券的长期理论价格，据计算，市场价格平均比理论价格低0.36%。Abe 等（2011）从利率角度解释了回购担保债券开发商购买股票的原因，并研究了套利的诱因，指出回购后公司的股票流动较少，有助于股价的稳定和资本结构的改善。

（二）国内文献综述

国内学术界结合我国国情对可转换债券进行了研究，但由于我国资本市场建立时间比较晚，可转换债券市场的发展时间也较短。相比国外，国内的可转换债券定价和交易策略相关的学术研究仍存在一定的差距。李运、石建民（1998）分析认为，可转债发行公司的价格核心是可转换价值和累计利率的有效组合，这意味着在可转换债券的流通和最终转换出现暂时的市场定价偏差时,可将其转换成股票,以期获取超额收益。秦学志、吴冲锋 （2000） 建立了二叉树模型，用实证分析解释了博弈机制的定价过程，并在博弈机制中得到了可转换债券的定价模型。王承讳、吴冲锋 （2001） 研究了转售条款和偿还条款的价格，在分析了两者对可转债价值影响的基础上，提供了蒙特卡罗模拟和有限差分数值算法，最终得出转售条款和偿还条款对可转换债券总价值影响有限的结论。杨如度等（2002）根据Hull-White 模型分析可转换债券价值驱动因素，分析转换和回购的期权特性，通过分析机场转移债务的数据，最终认为可转换债券与利率波动没有太大关系。王竹芳等（2005）运用算子分裂技术，考虑和分析了随机利率下的可转债定价模型。麦强、胡运权（2006）在蒙特卡罗算法的基础上找到了好的方法，获得了可转换债券的价格，按市场价格对其进行了检查，认为我国可转换债券的表现较低。乔高秀、潘席龙（2013）提出在股价反弹扩散过程中，带有违约风险的可转换债券定价模型能将可转换债券的债券性和股性相结合，可解释可转换债券市值低于理论价值的跳跃扩散过程，表明可转换债券存在被市场低估的现象。王一鸣等（2015）研究发现，在不确定的市场方向上，可转换债券的投资优势高于修正后的股票。王茵田和文志瑛（2018）研究了我国可转债的理论价格高于以往实际价格的事实，并指出修正条款能够减少可转让债务的价格误差，提高可转让债务的价格转换效率。

三、可转换债券定价的相关理论

（一）可转换债券的概念内涵

可转换债券是一种混合型证券，是公司普通股与证券期权的组合体。可转换债券的持有人在一定期限内，可以按照当时规定的价格或转换比例，自由选择是否行权将债券转换为公司的普通股。也就是说，可转债是一项具备多重性质的融资工具。可转换债券一般都有赎回条款和回售条款，赎回条款是指发债公司在可转换债券进行转换前，可按一定的条件赎回债券，通常公司股票在一段时期内一直高于转股价格达到一定幅度时，公司会按事先约定的价格买回未转股的可转换债券；回售条款是指公司股票价格在一段时期内一直低于转股价格到达一定的幅度时，债券持有人可按事先约定的价格将所持有的债券回售给发行公司。

（二）可转换债券的价值构成

可转换债券的价值可区分为两部分，一是债券价值，二是转股价值。债券价值，也称可转换债券纯债部分的价值，是指债券未转换为股票之前的价值。在计算债券价值时，所涉及到的主要指标有：每年的利息、无风险收益率、期限和面值大小。其中无风险收益率一般用国债的收益率来计算。转股价值是指可转债转为普通股之后的价值，也可称为期权价值。在计算转股价值时，涉及到期权类型的不同，计算期权价值的方法较多，因此，相对来说计算转股价值比较复杂。在计算可转债债券价值时采用的利率会比公司发行普通债券利率和同期银行存款利率低，若可转债持有者不行使转换的权力，所得到的利息相对来说是比较低的。因此投资者购买可转换债券所取得的收益主要来源自可转债转股的价值，转股价值的高低主要根据转换股票的价格、转换股票的比例以及转换股票的期限等因素进行具体的分析。

（三）可转换债券价值的影响因素

1.发行公司的股票市场价格。股票市场价格影响了转股期权的价值，回售、赎回和向下修正的条款都以股价为依据，因此股价在某些程度上决定了可转债价格波动的方向。一般来说，可转债的价格会随着股价的上涨而同方向变动，但当股票价格降低到一定幅度时，可转债可能会触及到回售条款，价格会随着股价的下跌而上涨。

2.股票价格波动率。影响可转债的一个重要因素是股票价格的波动率，股价波动率的大小与转股的可能性相关。波动率越大，可转债在未来涨到转股价格的可能性就越大，投资者行权的可能性也越大，可转债的价格会更高。

3.转股价格。转股价格的大小与未来可以转换股票的股数多少有关。转股价格越高，表明投资者在以后将可转债转为股票的数量越少，可转债的价值也会越低，可见转股价格与可转债的价值呈负相关关系。

4.转换期限。转换期限主要与期权部分的价值相关，且两者会呈现同方向变化，当期权价值增加时，投资者未来获得的利润可能会越高。

5.无风险利率。无风险利率的大小主要取决于市场利率的大小，一般会影响到可转债期权部分的价值。在股票价值没有发生变化的前提下，较高的利率会让行权的价格现值偏低，提高了看涨期权价值。

四、可转换债券定价和交易策略分析

（一）可转换债券定价模型

1.可转换债券期权定价模型的选择。可转换债券定价的难点在于如何确定期权部分的价值，目前学术界对期权部分的定价方法主要有三种：Black-Scholes 定价模型、二叉树定价模型和有限差分法。相较于Black-Scholes 定价模型，二叉树定价模型和有限差分法在处理美式期权时更有优势，但这两种方法计算量太大，计算过程中出现错误的概率较高。Black-Scholes 定价模型的计算过程简单方便，不易出错，只要将其中的固定参数计算出来，后将参数数值代入公式进行计算就能得到一个准确的数值，不但可为可转债的定价奠定数理基础，还可拓宽期权定价的研究。在分析三种定价方法的优缺点后，本文采用Black-Scholes 定价模型对可转债定价进行研究，并根据研究结果选择适合的交易策略。

2.Black-Scholes 模型。

（1）Black-Scholes 模型的假设。Black-Scholes 模型是麦伦-斯科尔斯和费舍尔-布莱克提出的针对欧式期权定价的专门的定价公式。该模型假设包括：①投资者对可转债的投资是持续的；②可转债的价格服从几何正态分布；③不考虑交易成本和税收等费用；④期权在持有期间，没有股票分红；⑤无风险收益率是常数；⑥市场上允许做空，不存在无风险套利的机会；⑦计算的是欧式期权，在持有期间不进行转股。

（2）可转换债券价值计算方式。可转换债券的价值包括纯债部分和期权部分，通过公式（1）可计算出纯债部分的价值，通过公式（2）可计算出期权部分的价值。

其中，B 代表可转债纯债部分的价值，I 代表债券的票面利息，n 代表可转债的期限，M 代表债券面值。

其中，C 代表可转换债券的期权价值，S 代表股票的当前价格，X 代表期权的实施价格，d1和d2分别用公式（3）和公式（4）进行计算，N（d）为正态分布变量的积累可能性分布函数。

其中，T 代表可转换债券期权剩下的有效期限，用相对数来表示，如可转换债券的有效期还剩100 天，一年按照365 天计算，则T=100/365 ≈0.274。

其中，σ 代表市场的标准偏差，代表着股票的波动情况。

（二）案例选择和介绍

近些年来，国家一直致力于发展电子通信行业以及医保行业，特别是5G 网络的发展以及2018 年国家医保局的成立，为人们的生活带来便利的同时，也提高了生活水平。从2019 年底开始，新冠疫情给国内外的医疗行业带来前所未有的挑战，而机遇与挑战并存，因此本文在综合考虑后选择电子通信行业的7 支可转债和医药生物行业的3 支可转债进行价值研究及交易策略分析。

集思录网站中收集到的电子通信行业的可转债共有33 支，在2019 年度期间共有7 支，分别是艾华转债（113504）、大族转债（128035）、盛路转债（128041）、中天转债（110051）、长信转债（123022）、亨通转债（110056）、永鼎转债（110058）；医药生物行业的可转债共有33 支，其中在2025 年12 月30 日到期的可转债有12 支，综合12 支可转债存在的期间、基本面的评级考虑，最终选取了在2020 年度AA-及以上等级的三支可转债作为案例样本，分别是溢利转债（123018）、现代转债（110057）、华森转债（128069），期限均为6 年，表1 和表2 是可转债的基本信息。

表1 2019 年通信行业可转债的基本信息

表2 2020 年医药生物行业可转债的基本信息

（三）可转债的理论价值分析

1.相关数据的确定。为简便计算，本文在确定股票价格时选择了股票当日的收盘价格。在确定无风险利率时，通常认为发行的国债利率有较强的参照性，因此无风险利率选择了2019 年、2020 年发行国债的五年期限利率，分别为4.27%、3.97%。波动率的计算采取年波动率，如2020年1 月1 日的波动率，是2019 年1 月1 日到2019 年12 月31 日股票价格的平均波动率。表3 至下页表6 为2019 年、2020 年各季度可转债的收盘价格和波动率数据。

表3 2019 年各时点通信行业可转债的收盘价格数据 单位：元

表4 2020 年各时点医药生物行业可转债的收盘价格数据 单位：元

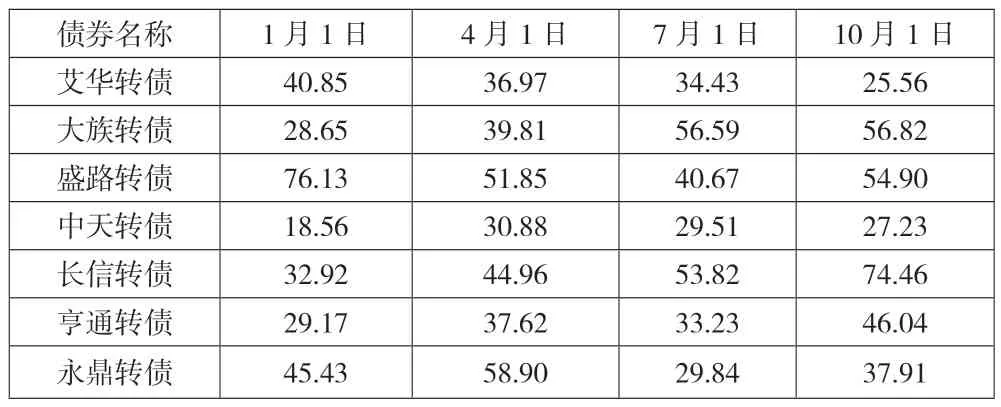
表5 2019 年各时点通信行业可转债的年波动率数据 单位：%

表6 2020 年各时点医药生物行业可转债的年波动率数据 单位：%

2.计算可转债的纯债价值。从东方财富网中查询可转债纯债价值的数据，整理得到下页表7 和表8。

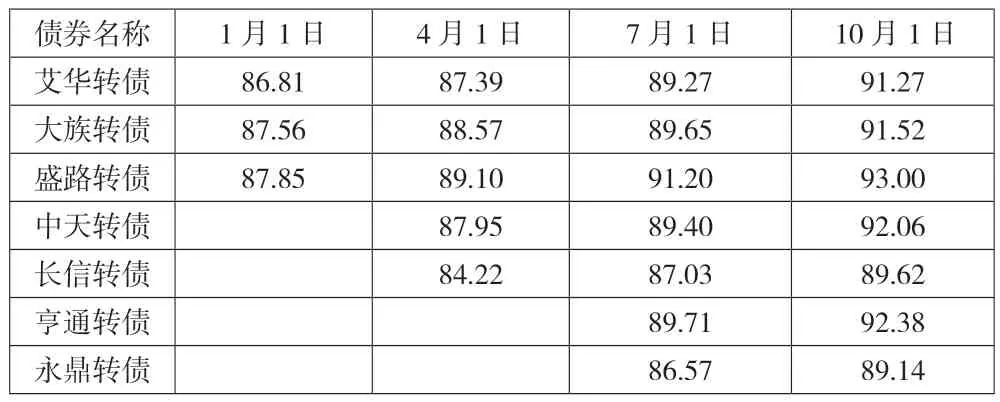
表7 2019 年各时点通信行业可转债的纯债价值 单位：元

表8 2020 年各时点医药生物行业可转债的纯债价值 单位：元

3.计算可转债期权价值。根据B-S 期权模型的相关公式，将数据代入公式计算各转债的看涨期权价值，如表9 和表10 所示。

表9 2019 年各时点通信行业可转债的期权价值 单位：元

表10 2020 年各时点医药生物行业可转债的期权价值 单位：元

4.计算可转债的理论价值。根据公式“理论价值=债券纯债价值+ 期权价值”，计算可得出可转债在2019年、2020 年各季度时间点的理论价值，如表11 和表12所示。

表11 2019 年各时点通信行业可转债的理论价值 单位：元

表12 2020 年各时点医药生物行业可转债的理论价值 单位：元

（四）2019 年各时点的交易策略分析

一般来说，判断可转债是否存在被资本市场低估的依据是比较在该时点上可转债理论价值与实际价值的大小。假设某可转债的理论价值比实际价值大，则表示该可转债往往存在被市场低估的现象。当可转债越被市场低估时，理论价值比实际价值大越多，表示可转债在将来上涨的几率越大。在选择投资可转债时，往往选择投资或持有被市场最低估的可转债更容易盈利，盈利的空间更大。反之，若某可转债的理论价值小于实际价值，则表示该可转债被市场高估，在未来上涨的几率不大，往往不选择该可转债进行投资。

以下对艾华转债（113504）、大族转债（128035）、盛路转债（128041）、中天转债（110051）、长信转债（123022）、亨通转债（110056）、永鼎转债（110058）在2019 年期间理论价值和实际价值的表现进行分析，在一年内按季度分为四个时间点进行分析，各时间点为每个季度的第一天，并于当日收盘时进行买进卖出。因可转债发行时间点不一致，因此每个期间可投资的可转债会略有变动。本文以100 万元作为原始投资。

1.2019 年第一季度交易策略分析。由表13 可知，在2019 年1 月1 日，艾华转债的理论价值为136.37 元，实际价值为104.00 元，两者相差32.37 元；大族转债的理论价值为143.73 元，实际价值为97.59 元，两者相差46.14 元；盛路转债的理论价值为157.49 元，实际价值为105.90 元，两者相差51.59 元。可见，在该时段上最被低估的可转债是盛路转债，其次是大族转债，最后是艾华转债，此时以当日收盘价买入最被低估的盛路转债，该时点盛路转债的实际价格是105.90 元，100 万元约可以买入94 手。

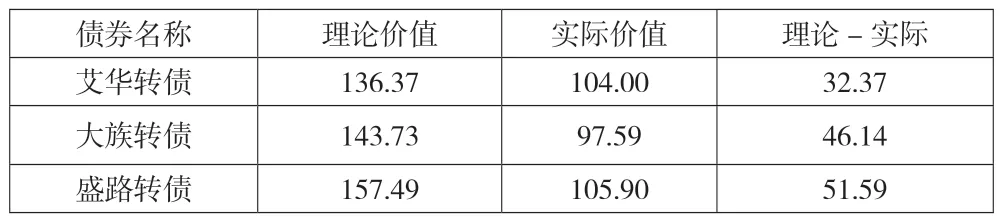
表13 2019 年1 月1 日部分可转债的理论价值、实际价值及差值 单位：元

2.2019 年第二季度交易策略分析。在上一季度买入盛路转债时，其理论价值为157.49 元，2019 年4 月1 日其理论价值为168.74 元，表明在这段期间某时点盛路转债已经达到买入时的理论价值，不再是被市场低估的可转债，应在该时点卖出。根据东方财富网的数据，在此期间，盛路转债的理论价值首次高于157.49 元的时点为2019年2 月25 日，其理论价值为172.33 元，故在2 月25 日以当日收盘价将盛路转债卖出，当天的实际价格是143.50元，卖出得到的金额是134.89 万元，收益共约34.89 万元，回报率为34.89%。由表14 可知，在2019 年4 月1 日收盘这一时点上，艾华转债的理论价值为138.62 元，实际价值为115.90 元，两者相差22.72 元；大族转债的理论价值为146.07 元，实际价值为112.36 元，两者相差33.71 元；盛路转债在该时点的理论价值为168.74 元，实际价值为156.50 元，两者相差12.24 元，中天转债在该时点的理论价值为136.86 元，实际价值为113.60 元，两者相差23.26元。可见，在该时点最被低估的可转债是大族转债，因此在该时点上以收盘价买入大族转债，此时的实际价格是112.36 元，将2 月25 日卖出盛路转债得到的金额买入大族转债，可以买入120 手。

表14 2019 年4 月1 日部分可转债的理论价值、实际价值及差值 单位：元

3.2019 年第三季度交易策略分析。在上一季度买入大族转债时，其理论价值为146.07 元，2019 年7 月1 日其理论价值为152.63 元，表明在这段期间某时点大族转债已经达到买入时的理论价值，不再是被市场低估的可转债，应在该时点卖出。根据东方财富网的数据，在此期间，大族转债的理论价值首次高于146.07 元的时点为2019年4 月9 日，其理论价值为147.01 元，故在4 月9 日以收盘价将大族转债卖出，当天的实际价格是112.40 元，卖出后账户总金额是135.92 万元，收益共约10 300 元，累计回报率为35.92%。由表15 可知，在2020 年7 月1 日这一时点上，艾华转债的理论价值为132.72 元，实际价值为105.30 元，两者相差27.42 元；大族转债的理论价值为152.63 元，实际价值为103.75 元，相差48.88 元；盛路转债的理论价值为152.06 元，实际价值为144.50 元，两者相差7.56 元；中天转债的理论价值为133.92 元，实际价值为106.40 元，两者相差27.52 元；长信转债的理论价值为149.12 元，实际价值为105.50 元，两者相差43.62元；亨通转债的理论价值为136.81 元，实际价值为99.55元，两者相差37.26 元；永鼎转债的理论价值为130.07 元，实际价值为95.14 元，两者相差34.93 元。可见，最被低估的是大族转债，若此时想要继续投资可转债，可以以当日收盘价买入大族转债，此时买入的实际价格是103.75 元，135.92 万元可买入130 手。

表15 2019 年7 月1 日部分可转债的理论价值、实际价值及差值 单位：元

4.2019 年第四季度交易策略分析。在上一季度买入大族转债时，其理论价值为152.63 元，2019 年10 月1日其理论价值为157.23 元，表明在这段期间某时点大族转债已经达到买入时的理论价值，不再是被市场低估的可转债，应在该时点卖出。根据东方财富网的数据，在此期间，大族转债在2019 年9 月23 日的理论价值高于152.63 元，为153.37 元，故在9 月23 日以收盘价格将大族转债卖出，当天的实际价格是107.00 元，卖出后账户总金额是139.15 万元，累计回报率为39.15%。由表16 可知，在2020 年10 月1 日，艾华转债的理论价值与实际价值相差22.05 元，大族转债的理论价值与实际价值相差50.23元，盛路转债的理论价值实际价值相差25.51 元，中天转债的理论价值和实际价值相差31.41 元，长信转债的理论价值与实际价值相差77.13 元，亨通转债的理论价值与实际价值相差49.00 元，永鼎转债的理论价值与实际价值相差46.65 元。可见，在该时点最被低估的是长信转债，若此时想要继续投资可转债，可以在当日以收盘价买入长信转债，此时买入的价格是124.00 元，139.15 万元可买入112 手。根据东方财富网数据，在2019 年10 月11 日，长信转债的理论价值为205.25 元，高于10 月1 日的理论价值201.30 元，故在该时点以收盘价卖出长信转债，此时的实际价格是127.00 元，卖出后账户总余额为142.51 万元，累计回报率为42.51%。

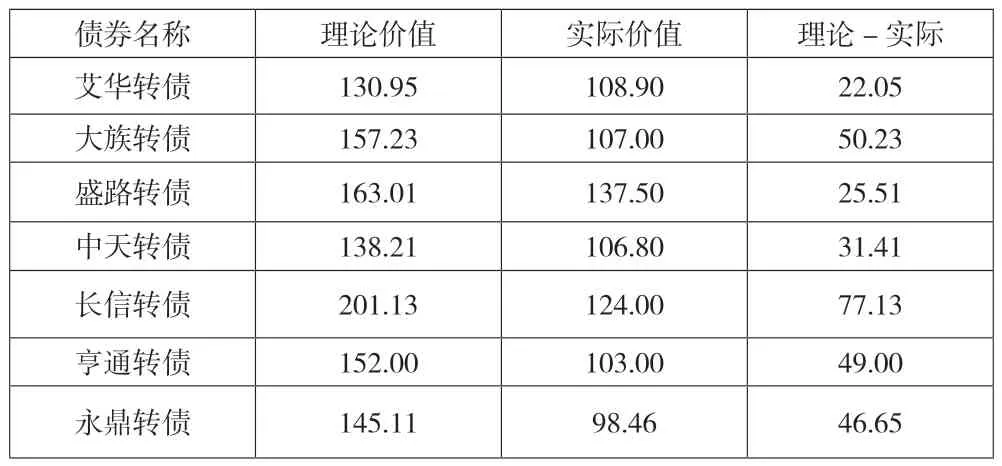
表16 2019 年10 月1 日部分可转债的理论价值、实际价值及差值 单位：元

（五）2020 年期间各时点的交易策略分析

以下对溢利转债（123018）、现代转债（11057）、华森转债（128069）在2020 年内的理论价值和实际价值表现进行分析，在一年内按季度分为四个时间点进行分析，各时间点为每个季度的第一天。

1.2020 年第一季度交易策略分析。由表17 可知，在2020 年1 月1 日这一时点，溢利转债的理论价值为129.93元，实际价值为122.15 元，两者相差7.78 元；现代转债的理论价值为134.59 元，实际价值为111.50 元，两者相差23.09 元；华森转债的理论价值为160.52 元，实际价值为107.25 元，两者相差53.27 元。可见，在该时点上最被低估的可转债是华森转债，其次是现代转债，最后是溢利转债，此时应买入最被低估的华森转债，该时点其实际价格是107.25 元，100 万元可以买入93 手。

表17 2020 年1 月1 日部分可转债的理论价值、实际价值及差值 单位：元

2.2020 年第二季度交易策略分析。由表18 可知，在2020 年4 月1 日这一时点上，溢利转债的理论价值为150.58 元，实际价值为139.50 元，相差11.08 元；现代转债的理论价值为154.06 元，实际价值为116.12 元，相差37.94元；华森转债在该时点的理论价值为157.91 元，实际价值为120.60 元，相差37.31 元。可见，在该时点最被低估的可转债是现代转债，其次是华森转债，最后是溢利转债。根据东方财富网的数据，从第一季度持有至该时间点期间，未出现理论价值大于买入点理论价值的时点，因此在2020 年4 月1 日以当日收盘价卖出原持有的华森转债，此时其实际价格是120.60 元，卖出后账户总金额是112.45 万元，累计回报率为12.45%。将得到的金额买入价格为116.12 元的现代转债，可以买入97 手。

表18 2020 年4 月1 日部分可转债的理论价值、实际价值及差值 单位：元

3.2020 年第三季度交易策略分析。在上一季度买入现代转债时，其理论价值为154.06 元，在2020 年7 月1 日时其理论价值为158.04 元，表明在这段期间某时点现代转债已经达到买入时的理论价值，不再是被市场低估的可转债，应在该时点卖出。根据东方财富网数据计算得出，在此期间，现代转债的理论价值首次高于154.06 元的时点出现在2020 年4 月15 日，其理论价值为155.58 元，故在4月15 日以收盘价格将现代转债卖出，当天的实际价格是119.00 元，卖出后账户总额是115.50 万元，累计回报率为15.50%。

由上页表19 可知，在2020 年7 月1 日这一时点，溢利转债的理论价值为201.98 元，实际价值为188.55 元，两者相差13.43 元；现代转债的理论价值为158.04 元，实际价值为110.25 元，两者相差47.79 元；华森转债的理论价值为155.93 元，实际价值为108.90 元，两者相差47.03 元。可见，在该时点最被低估的是现代转债，其次是华森转债，最后是溢利转债，若此时想要投资可转债，可以选择买入现代转债，此时以收盘价买入的价格是110.25 元，115.50 万元可买入104 手。

表19 2020 年7 月1 日部分可转债的理论价值、实际价值及差值 单位：元

4.2020 年第四季度交易策略分析。由表20 可知，在2020 年10 月1 日这一时点，溢利转债的理论价值为162.44 元，实际价值为195.28 元，两者相差32.84 元；现代转债的理论价值为132.27 元，实际价值为113.40 元，两者相差18.87 元；华森转债在该时点的理论价值为127.33元，实际价值为107.14 元，两者相差20.19 元。可见，在该时点最被低估的是华森转债，其次是现代转债，溢利转债没有呈现出被低估的信号。但因7 月1 日买入现代转债后，并未达到预期的理论价值，在10 月1 日已经不是最被低估的可转债，此时以收盘价格卖出现代转债，其实际价格是113.04 元，卖出后共可获得119.40 万元，累计回报率为18.40%。在2020 年1 月1 日投入100 万元，到2020 年10月1 日本金及利息一共是118.40 万元，本年投资收益金额约为18.40 万元，累计回报率为18.40%。

表20 2020 年10 月1 日部分可转债的理论价值、实际价值及差值 单位：元

（六）交易策略小结

在本文分析中，主要的交易策略思路是在拟定盈利目标后，寻找到被低估程度最大的可转债进行投资，如果此时持有的可转债是被最低估的，则选择继续持有；如若不是最被低估的可转债，则找出达到预期理论价值的时点进行卖出，后续再寻找最被低估的可转债进行投资。按照以上述交易策略进行投资，则2019 年的单年收益可以达到42.51%，2020 年的单年收益可以达到18.4%。两年的复利收益甚至可以达到68.73%。

五、结论与展望

本文首先基于Black-Scholes 模型对可转债的定价进行了研究，通过选取艾华转债等10 支可转债作为样本，对这些可转债样本在2019 年度、2020 年度期间的实际价格和理论价格进行分析，进而发现可转债样本在特定年度的四个时点的理论价格几乎均大于实际价格，存在被低估的现象，最后找到最被市场低估的可转债进行投资作为交易策略，确定买入及卖出的时点，对四个时点的情况提出了简要的交易策略。结果发现此简单的交易策略得到超常的收益，远超过普通的公司债券或者国债的利息。换言之，用Black-Sholes 模型进行简单的套利或者投资，能在A 股市场中得到超常收益，值得所有市场的参与者加以注意并做进一步研究。

可转债作为一种具有多重属性的金融衍生产品，其定价的过程是比较复杂的，涉及到的参数和方法也不尽相同，本文在选取案例样本时选择了基本面比较好、评级相对较高的可转债，在提出交易策略时只选择了最被市场低估的可转债进行投资，交易策略较为单一。此外，对可转债交易的分析还需要结合政策、经济发展等宏观因素做进一步的研究和完善。