列车双雷达测速算法优化
柯文雄, 姜 敏, 袁 伟,2,3, 涂 建,2,3, 李由之
(1.上海无线电设备研究所, 上海 201109;2.上海目标识别与环境感知工程技术研究中心,上海 201109;3.中国航天科技集团有限公司交通感知雷达技术研发中心, 上海 201109;4.上海神添实业有限公司, 上海 200090)
0 引言
测速系统在轨道列车的行驶控制中起到重要作用,是保障列车安全、高效运行的基础设施。随着轨道列车运行速度不断提升,列车对测速系统的精确性和可靠性要求越来越高。多普勒测速雷达利用列车相对地面运动的多普勒效应进行测速,具有全天候、实时、高精度的优点,有良好的应用前景[1-3]。
在实际使用中,列车颠簸和地形变化会引起多普勒测速雷达波束擦地角的变化。直接利用单雷达的多普勒频率测量值计算列车速度时,雷达波束擦地角的变化会导致雷达测速精度降低。采用双雷达联合测量的方法可以消除颠簸和地形的影响[4]。但是当雷达测量得到的多普勒频率与列车速度对应的多普勒频率误差较大时,联合双雷达测量信息解算得到的列车速度将与实际列车速度存在较大误差。因此,只有综合考虑列车颠簸、地形变化和多普勒频率测量误差的影响,才能得到更高的测速精度。
本文在分析角度误差和多普勒频率误差对雷达速度解算精度影响的基础上,提出一种基于径向基函数网络(radial basis function neural network,RBFNN)的双雷达测速方法,并通过仿真分析和实际数据对比,证明该方法的正确性。
1 测速原理
多普勒雷达向地面发射电磁波并接收地面回波,从回波中提取列车相对地面运动时的多普勒频率。可采用单雷达的直接法及双雷达联合法进行多普勒频率测量和速度解算。
(1) 直接法
利用单雷达测量得到的多普勒频率,可直接解算出列车速度
式中:fD为多普勒信号频率;λ为雷达发射信号波长;θ为雷达波束擦地角。
在实际使用过程中,受列车颠簸和地形变化影响,多普勒雷达波束擦地角会偏离真实值,导致雷达测速精度降低。采用单雷达的直接法难以满足测速精度要求。
(2) 双雷达联合法
双雷达联合测速能够有效解决波束擦地角偏离真实值导致的测速精度降低问题。双雷达测速系统的雷达安装方式如图1所示。两部雷达采用刚性连接方式同向安装在列车底部,同时进行独立测量。图中θ1,θ2分别是雷达1和雷达2的波束擦地角。
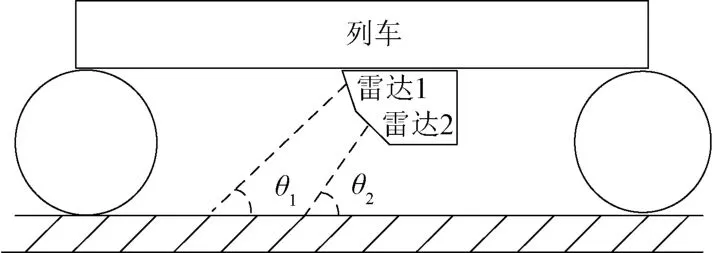
图1 双雷达测速系统的雷达安装方式示意图
设雷达1和雷达2测量的多普勒频率分别为fD1,fD2,则列车速度
刚性连接的两部雷达波束方向与地面夹角的角度差Δθ=θ2-θ1在整个列车运行过程中恒定,因此式(2)可消去θ1和θ2,得到不受θ1和θ2约束的列车速度计算公式,即
2 多普勒频率误差对测速误差的影响
两部雷达同时独立进行测量,因此其测量的多普勒频率误差可视为互相独立的随机变量。假设在列车运行过程中,雷达1和雷达2的多普勒频率测量误差分别为ΔfD1和ΔfD2,通常有ΔfD1≪fD1,ΔfD2≪fD2。
使用直接法解算列车速度,则雷达1和雷达2的测量速度可以表示为
列车的运行速度v1可以用两部雷达测量速度的平均值表示,即
因此使用直接法解算列车速度,列车速度误差可以表示为
根据式(3),使用双雷达联合法解算列车速度,列车速度误差Δv2可以表示为
两部雷达间的Δθ越小,雷达的照射范围越接近,因此在实际轨交环境下,通常需满足cosΔθ≈1。雷达波束擦地角越小,多普勒速度模糊越严重,因此在实际应用时雷达波束擦地角通常比较大,满足cosθ>sinΔθ。此时式(8)可简化为
在满足条件ΔfD1≪fD1,ΔfD2≪fD2情况下,由式(7)和式(9)可知,列车实际运行速度大小对列车测速误差的影响不大。
模拟两部24 GHz多普勒雷达进行列车速度测量,其中雷达1的波束擦地角为60°,雷达2的波速擦地角为50°。列车速度为20 m/s时,在两部雷达测量的多普勒频率理论值上分别叠加(0~30)Hz相互独立的随机误差。每个误差下进行300次模拟计算,采用误差绝对值的平均值表示该多普勒频率测量误差下解算的列车速度误差。
分别采用直接法和双雷达联合法测量的多普勒频率误差与速度误差关系如图2所示。两种方法解算得到的速度误差都随着多普勒频率测量误差的增加而线性增加,以多普勒频率测量误差30 Hz的情况为例,采用直接法的速度误差均值为0.062 m/s,而采用双雷达联合法的速度误差均值为0.358 m/s,双雷达联合法测量速度误差约为直接法的5.8倍。
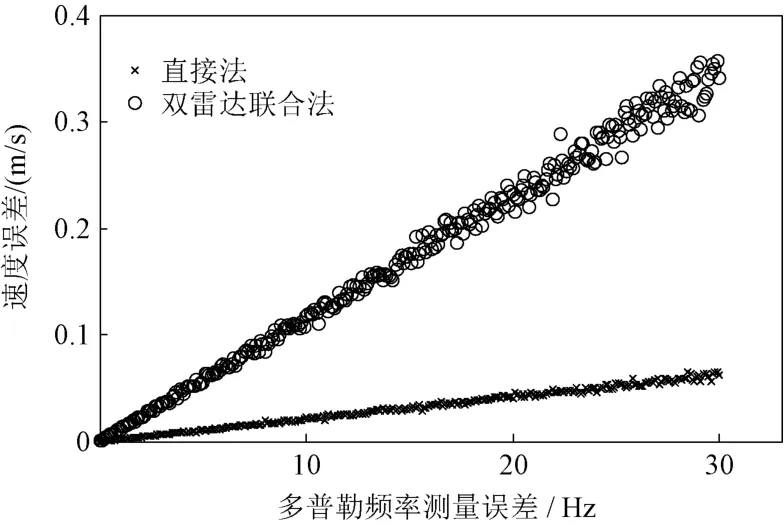
图2 直接法和双雷达联合法测量速度误差曲线
3 基于RBFNN 的双雷达测速法
通过前文误差分析可知,双雷达联合测速虽然能消除角度偏离带来的影响,但对于多普勒频率的测量误差更敏感。
为了解决该问题,本文提出基于RBFNN 的双雷达测速算法。在保留角度修正能力的前提下,提高多普勒频率误差较大时的速度解算精度。具体步骤如下。
步骤1:通过RBFNN 计算列车预测速度。
速度的延滞特性为RBFNN 应用提供了基础[5-6]。在列车运行的整个过程中,列车速度的大小和方向均不会出现瞬间突变,符合径向基函数预估值判断原理。
RBFNN 属于有监督学习,是以函数逼近理论为基础构造的前向网络。该算法采用保证全局收敛的线性算法,可以根据列车速度的数据特点确定网络拓扑结果,具有自学习、自组织、自适应能力。因学习速度快,且具有唯一最佳逼近点,可以并行高速处理数据,该算法能够满足实时在线应用需求。
RBFNN 由三部分组成,分别为输入层、隐藏层、输出层。在t时刻,选取前n个列车速度数据组成输入速度序列Vt=(vt-n,vt-n+1,… ,vt-1)作为RBFNN 网络的训练集,因此RBFNN 神经网络存在n个输入。设ve为RBFNN 在t时刻输出的预测速度,即
式中:N为隐藏层数量;ωi为第i个隐藏层的权值;φi为第i个隐藏层基函数;‖Vt‖ 表示速度的欧几里得距离。
步骤2:通过直接法和双雷达联合法解算列车速度。
基于式(6),采用直接法解算t时刻列车的运动速度
采用双雷达联合法解算t时刻列车的运动速度
步骤3:比较直接法和双雷达联合法解算结果的可信度。
在列车运行的过程中,同时存在颠簸等原因造成的角度偏离预定值和电磁干扰造成的多普勒测量值偏离真实值的问题。在不同时刻、不同环境下,雷达的角度误差和多普勒频率测量误差的大小不同,因此两种方法解算出来的列车速度的可信度也不同[7-8]。
通过比较解算速度v1,v2与RBFNN 预测速度ve之间的误差d1,d2,来表征两解算速度的可信度。双雷达解算速度误差d1,d2的表达式为
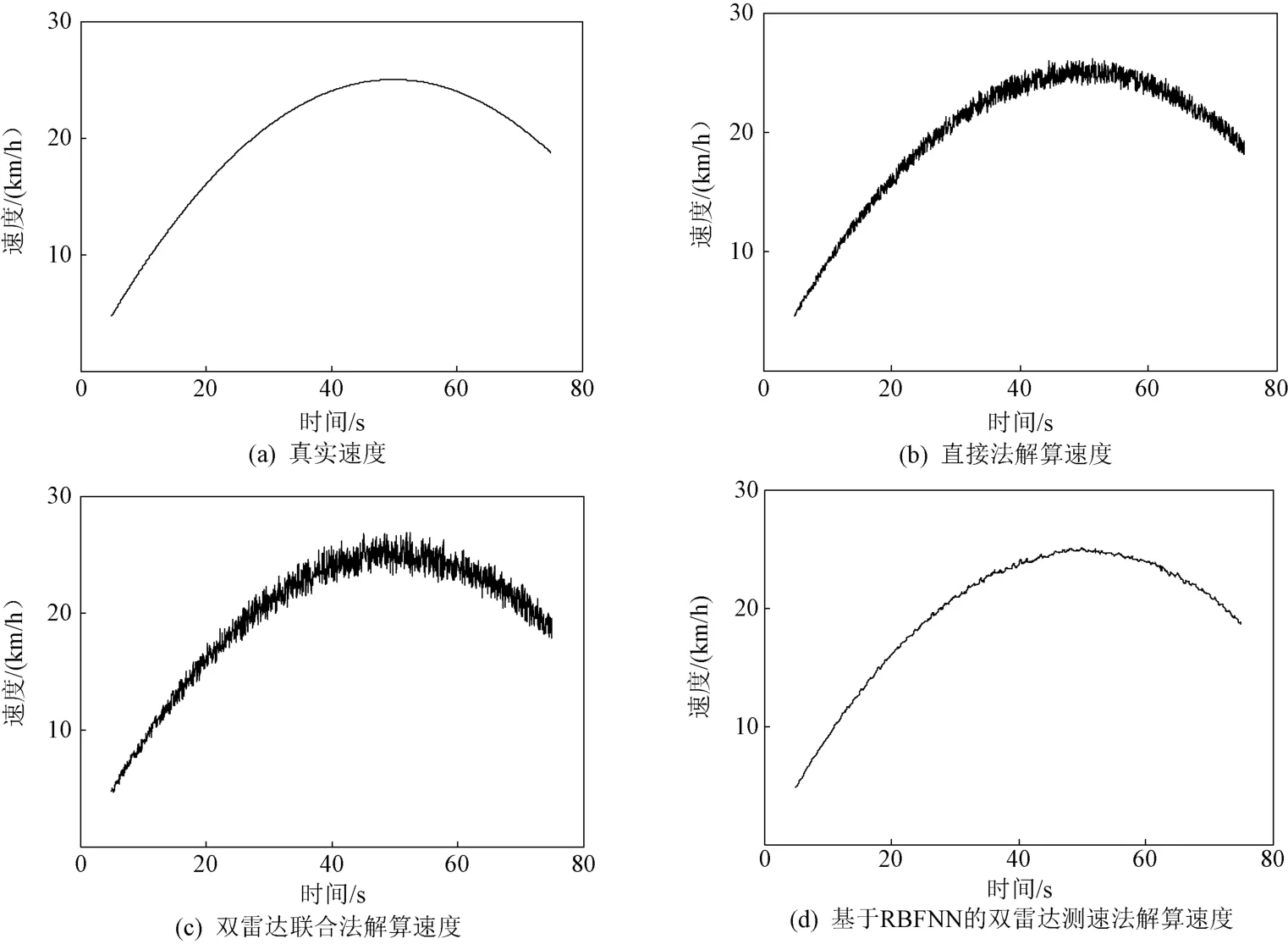
若d1 步骤4:判断可信速度值是否处于置信区间。 在列车运行过程中,雷达会因电磁环境干扰、剧烈振动、电源不稳等因素而工作异常。此时直接法和双雷达联合法解算出来的速度均不可信,应当舍弃。 本文通过确认步骤3计算的速度误差是否落入置信度区间来判断雷达是否工作正常[9]。如果速度误差落入置信区间,则认为雷达工作正常,解算速度准确,以vr作为t时刻实测速度vt;反之,则认为雷达工作异常,解算速度出错,以RBFNN预测值ve作为t时刻实测速度vt。 步骤5:重复计算。 将经步骤4得到的速度vt代入,生成新训练集Vt+1=(vt-n+1,vt-n+2,… ,vt)。重复步骤1~步骤5,实现对列车速度的实时解算。 整个算法流程如图3所示。 图3 测速算法流程图 为了验证上述算法的有效性,对速度解算过程进行仿真。模拟两部24 GHz多普勒雷达进行列车速度测量,其中雷达1的波束擦地角为60°,雷达2的波速擦地角为50°。在实际列车运行环境下,列车的波束擦地角误差范围一般不大于3°,因此为雷达波束擦地角叠加±1.5°的随机角度误差。雷达的多普勒频率测量误差不大于3%,因此对雷达的多普勒频率叠加±1.5%的随机频率误差。 不同方法解算得到的速度曲线如图4所示。其中图4(a)为真实速度曲线;图4(b)为直接法解算速度曲线,解算速度与真实速度之间误差的平均值为0.383 4 km/h、标准差为0.266 6 km/h;图4(c)为双雷达联合法解算速度曲线,解算速度与真实速度误差的平均值为0.555 7 km/h、标准差为0.417 5 km/h;图4(d)为本文基于RBFNN的双雷达测速法解算速度曲线,解算速度与真实速度误差的平均值为0.148 2 km/h、标准差为0.106 6 km/h。基于RBFNN 的双雷达测速法解算速度的标准差、方差都远小于直接法和双雷达联合法解算的结果。可以看出,本文方法能够有效提高雷达的测速精度。 图4 不同方法的解算速度曲线 直接法测速会因雷达波束擦地角变化而导致测速精度降低。双雷达联合测速虽然能消除角度变化的影响,但对多普勒测量值与真实值之间的误差更敏感。本文提出一种基于RBFNN 的双雷达测速算法,经过仿真验证能够有效提高雷达的测量精度。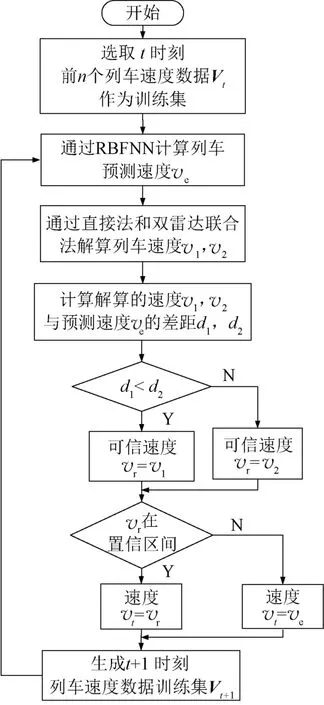
4 仿真验证
5 结论

