水平转弯状态旋翼气动噪声特性计算分析

李志彬,张羽霓,王雪鹤,林永峰

(中国直升机设计研究所 直升机动力学全国重点实验室,江西 景德镇 333001)

0 引言

噪声大直接限制了直升机在军用领域的生存能力和民用领域的适航范围,气动声学设计也因此成为现代直升机设计过程中重要的研究内容。

旋翼噪声作为直升机的主要噪声之一[1-2],因其频率低、传播远的特性而备受关注。当前,直升机的主动和被动降噪设计[3-4]一般会导致其它关键性能参数的降低,比如前飞升阻比等。此外,主、被动降噪设计由于要改变旋翼结构,并不能直接应用于现役直升机。调整直升机飞行轨迹和姿态的“使用降噪技术”是一种具有潜力的低成本直升机降噪方法。实施这一技术对旋翼结构不产生影响,因此,低噪声飞行轨迹设计成为了拓展直升机任务范围最有希望的途径之一[5-7]。

水平转弯是一种非常重要的飞行姿态,是直升机完成部分复杂机动动作的前提[8]。研究并掌握水平转弯状态不同飞行参数下的旋翼气动噪声特性,对直升机低噪声轨迹设计具有重要意义。从公开文献来看,国内外对水平转弯状态下的旋翼气动噪声研究较少。国外主要通过试验测试方法研究了转弯状态与直升机直线飞行的噪声区别,发现转弯状态噪声显著增大[9]。国内南京航空航天大学朱晨帆[10]通过准定常映射的计算方法,引入二级声辐射球的概念建立了水平转弯状态下地面声场的计算方法,但缺乏旋翼气动力分析和噪声指向性分析。

鉴于此,本文基于Camrad II/FW-H旋翼噪声快速计算模型,在相同转弯半径下计算了前进比对旋翼气动噪声的影响,并基于二级声辐射模型,分析了前进比对地面辐射声场的影响,得出了一些有价值的结论。

1 计算方法

1.1 非定常载荷计算

为快速获得旋翼桨叶的非定常气动力,本文采用Camrad II计算旋翼桨叶的非定常气动载荷。在计算模型中,每片桨叶采用11个非线性梁单元建模,每片桨叶包含15个桨叶载荷(升力系数、阻力系数)输出剖面。为了更好地捕捉桨-涡干扰现象,一个旋转周期采用360个方位角来描述,分辨率为1度。旋翼入流计算采用自由尾迹几何模型,升力被分解到桨叶固定坐标系中,然后通过Camrad II数据后处理程序从结果文件中提取配平后操纵量以及旋转时间的相关函数(方位角、展向位置、当地马赫数、升力系数)。

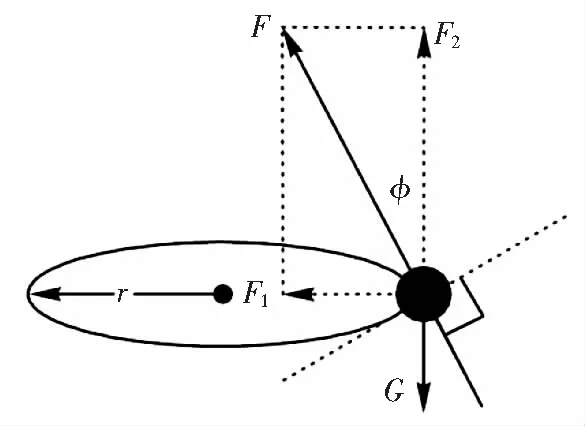
图1 水平转弯受力分析图

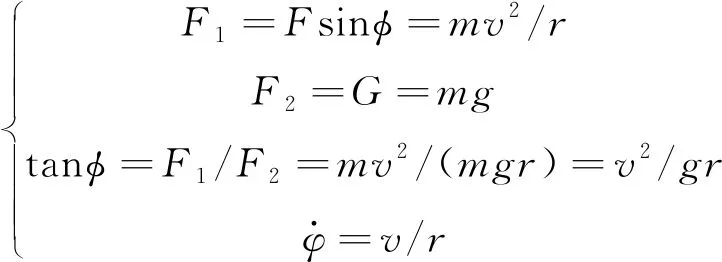
(1)

所以对于某一前飞速度和转弯半径,通过式(1)计算得到水平转弯需要的坡度角和偏航角速率,代入Camrad II计算模型进行旋翼载荷计算。

1.2 噪声计算方法

FW-H方程是气动噪声计算经典方程。对于亚音速状态的旋翼噪声,Farassat 1A公式(以下通称F 1A公式)是FW-H方程解的时域积分表达式。为了使用Camrad II计算得到的桨叶剖面气动力,基于紧致源模型,将F 1A公式中的载荷噪声部分写成紧致源形式[11-12]:

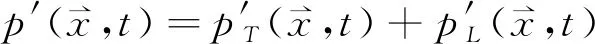
(2)

式中,

(3)

(4)

式中,L为截面升力矢量,R为桨叶半径,y是紧致源点所在径向位置。

在公式(4)中,桨叶表面载荷分布体现为桨叶截面升力在桨叶中弧面四分之一弦长处的集中分布。

1.3 方法验证

为了验证本文噪声计算方法的可靠性,在中国空气动力学研究与发展中心4 m×5.5 m声学风洞开展了模型旋翼声学验证试验。

试验中模型旋翼直径为2 m,具有5片桨叶。桨叶采用OA系列翼型,桨尖抛物线后掠,线性负扭转。试验中桨尖转速为208.3 m/s(95%额定桨尖速度环境修正值)。图2给出了桨盘平面内和桨盘夹角20°处声压历程的本文计算值与试验值对比。

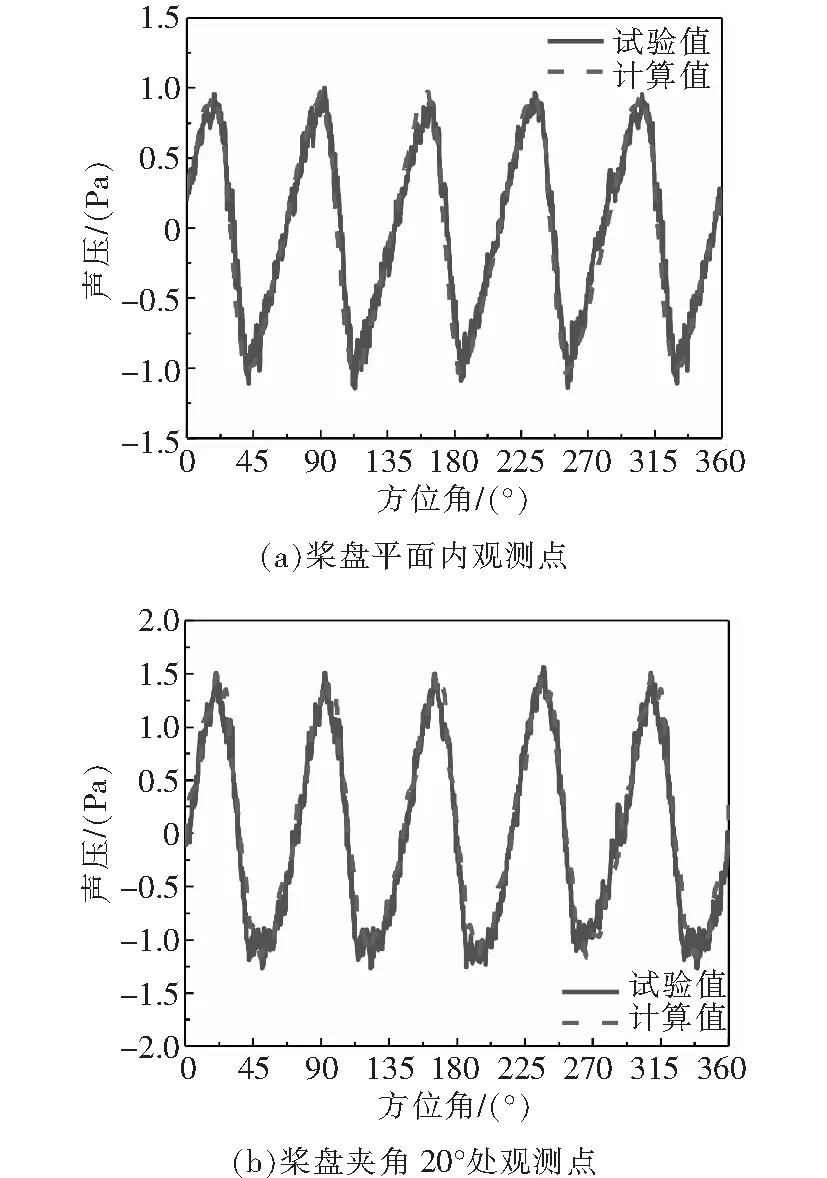
图2 模型旋翼声压时间历程对比

从图中可以看出,本文采用旋翼噪声计算模型计算得到的观测点处的声压历程与试验值吻合得很好,表明了本文方法的有效性。

2 噪声计算分析

2.1 计算模型方法验证

本文计算采用的直升机旋翼有5片桨叶,旋转方向为俯视逆时针,采用NACA系列翼型,桨尖抛物线后掠,采用线性负扭转。采用拉力式尾桨,旋转方向为底向前。对于逆时针旋翼,每一种转弯都有不同的尾迹干涉和声学特性,因此左、右转弯都进行评估。

本文研究结果可以用于辅助驾驶员实现低噪声轨迹飞行。考虑到驾驶员一般无法估计转弯半径,因此在表1中列出了Camrad II计算得到的转弯半径、前飞速度和坡度角的对应关系,其中R为旋翼半径,φ为坡度角。从表中可以看出,在转弯半径相同的情况下,坡度角随前飞速度增大而增大。相同飞行速度下,左转弯对应坡度角比右转弯大。左、右转弯坡度角不对称是由于旋翼桨叶在前行侧和后行侧入流速度的差异,以及全机配平差异(尾桨拉力方向)造成的。

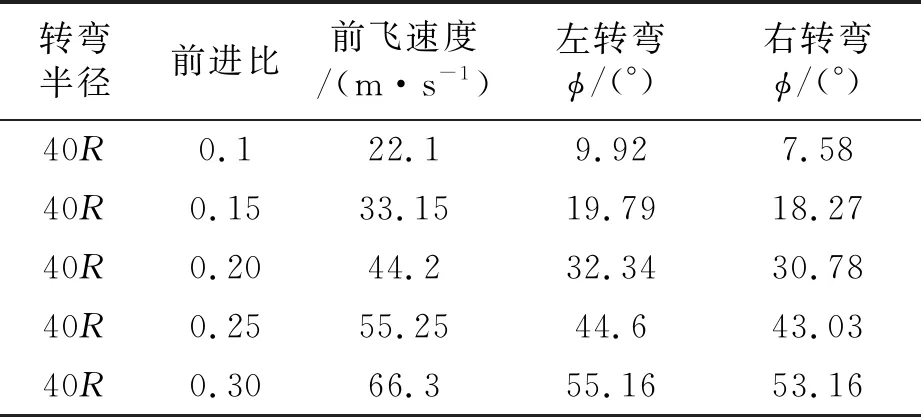
表1 转弯半径与前飞速度对应关系

为了分析旋翼的气动噪声特性,以旋翼桨毂中心为球心,取1387个观测点组成的半径为25R的声辐射半球。声辐射半球是水平固定的,不随旋翼坡度角变化,如图3所示。在后续分析中,将半球面以Y正半轴等角割圆锥投影转换,得到声辐射半球的Lambert投影。

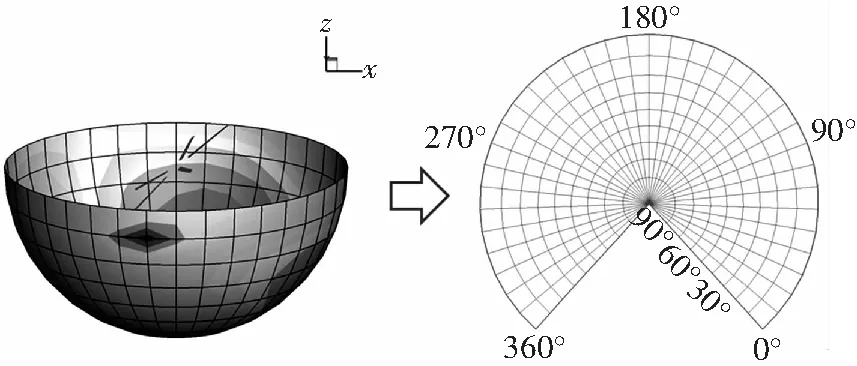
图3 左转弯状态声辐射半球示意图

2.2 不同前进比旋翼噪声特性

图4和图5给出了左转弯和右转弯状态下旋翼气动噪声云图。从图中可以看出,左转弯状态对应辐射半球的噪声热点区域相比于右转弯状态偏右。本文定义噪声级较大区域为噪声热点区域,噪声级较小区域为噪声冷点区域。

左转弯状态下,随着前进比的增大,噪声热点区域逐渐向方位角较小、桨盘夹角较小区域偏移。从图4中96 dB等值线环绕面积可以看出,随着前进比的增大,辐射噪声先减小后增大。

图4 左转弯状态旋翼气动噪声云图

右转弯状态下,随着前进比的增大,噪声热点区域逐渐向方位角较大、桨盘夹角较小区域偏移。从图5中98 dB等值线环绕面积可以看出,随着前进比的增大,辐射噪声呈脉动变化,无明显规律。

图5 右转弯状态旋翼气动噪声云图

2.3 不同前进比旋翼气动力分析

图6分别给出了前进比0.2时左、右转弯状态旋翼尾迹的俯视图、侧视图和后视图。从图中可以看出,前行侧干涉强,后行侧干涉相对较弱。这是涡旋对流的结果,也是因为横向周期变距控制桨叶在前行侧挥舞下降,在后行侧挥舞上升。比较图6(e)和图6(f)可以看出,右转弯在前行侧尾迹更加集中,桨涡干扰会更加强烈,所以右转弯对应的噪声相对较大。

由旋翼载荷噪声计算公式(4)可知,旋翼载荷噪声与桨叶气动载荷的脉动量直接相关。为了进一步分析2.2节旋翼噪声级变化的原因,图7和图8给出了旋翼桨叶展向位置0.875R、0.9475R两个截面的升力在桨叶旋转一周内的变化规律。

从图中可以看出,桨叶剖面升力在60°～120°和240°～300°方位角范围内均发生了不同程度的振荡,这是由于桨涡干扰导致的。从图7可以看出:前进比0.1状态的升力曲线在方位角90°附近发生多次明显振荡;相比之下,前进比0.25状态的升力曲线在方位角90°附近振荡明显较小,桨涡干扰现象减弱。所以,前进比0.25状态的噪声要明显小于前进比0.1状态。从图8可以看出,在方位角90°附近,前进比0.15状态的升力曲线发生了多次明显振荡,其余状态振荡程度明显较小。因此,前进比0.15状态是右转弯状态中噪声最大的。

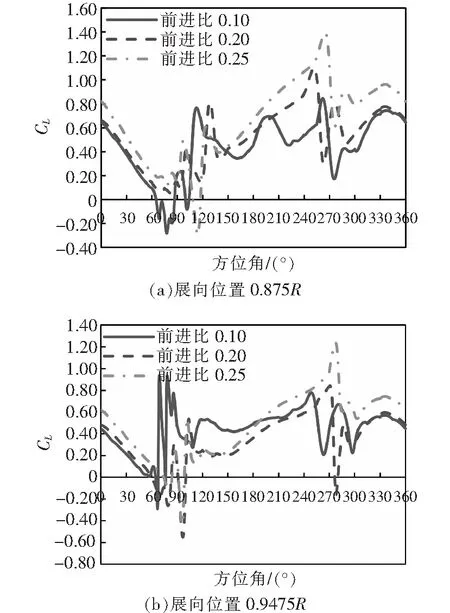
图7 左转弯状态旋翼桨叶非定常气动力

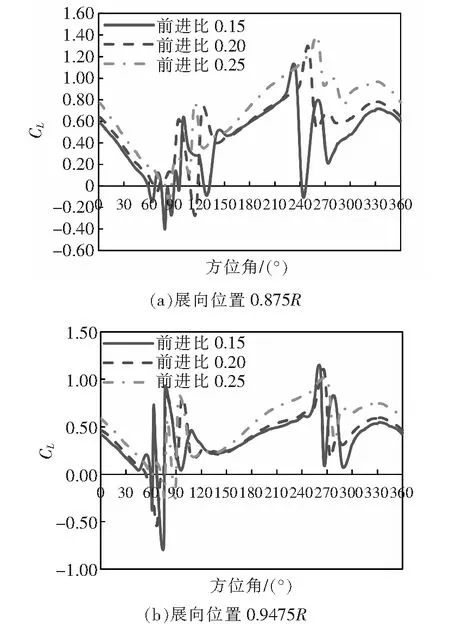
图8 右转弯状态旋翼截面升力随方位角的变化

从以上分析可以得出,左转弯前进比0.1状态和右转弯前进比0.15状态为桨涡干扰最强状态,此时桨-涡干扰噪声占优。随着前进比进一步增大,直升机坡度角增大,旋翼拉力增大,此时旋翼拉力对于噪声占主导地位。

图9给出了左转弯两个状态典型观测点处的声压时间历程,其中典型观测点分别位于两个状态辐射半球上的噪声级最大处。从图中可以看出,前进比0.1状态在方位角20°附近存在明显的声压正峰值,这是桨-涡干扰状态的典型特征,说明此时旋翼噪声主要是BVI噪声。而前进比0.25状态无明显的桨-涡干扰现象。

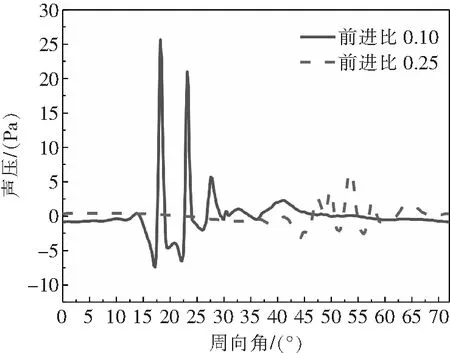
图9 典型观测点试验时间历程对比

3 地面声场计算分析

本节基于二级声辐射模型完成地面声场的快速预测[13]。针对转弯飞行,将轨迹分成一系列连续的轨迹段,将每一段轨迹称之为轨迹元素,元素间距对应直升机旋转一圈行进的距离。取每一段轨迹的中间为控制点,每个控制点对应了不同状态的声辐射球数据;再通过二级声辐射球模型进行地面点定位,辐射到地面观测点上,得出本文需要的地面声场数据。

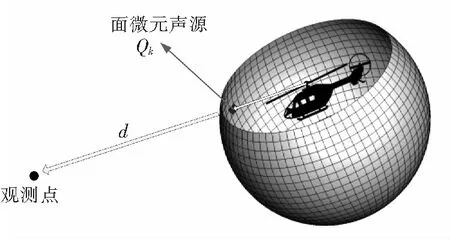
图10 二级声辐射球模型[13]

3.1 地面声场特性

为了方便对比,转弯飞行轨迹以(0 m,0 m,500 m)为固定经过点,观测点均位于地面(Z=0 m),转弯角度为180°,转弯半径为40R,如图11所示。

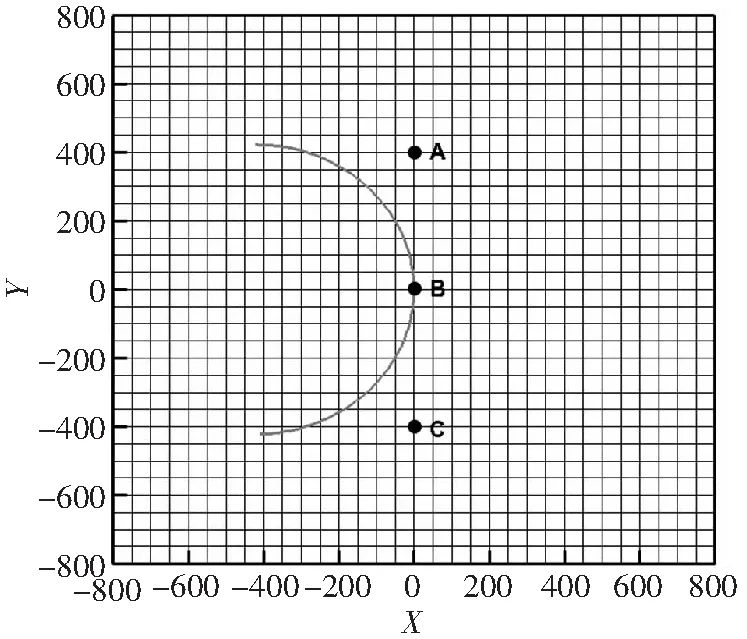
图11 地面观测点示意图

地面声场采用等效连续声级(LEQ)作为度量,单位以dB表示。LEQ表示在声场中某一位置上某一段时间内的噪声大小,是将连续变化的声级以时间能量平均的方法计算出来的。通过LEQ在观察平面上的等高线图确定了相关轨迹的“相对噪声”。这说明LEQ可便于量化每条轨迹的“持续噪声影响”,可用于定性地判断一条飞行轨迹相对于另一条飞行轨迹的“良好性”。等效连续声级的计算公式:

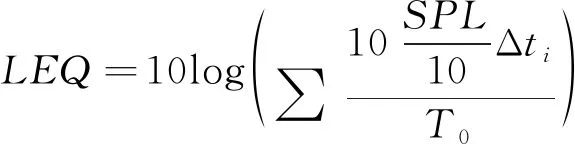
(5)

式中,Δt表示旋翼旋转一圈的时间,下标i表示飞行轨迹离散点的编号,T0为某段时间的总量。

图12和图13分别给出的是左转弯、右转弯状态旋翼噪声辐射的地面声场。在本文的研究范围内,与右转弯相比,左转弯的等效连续声级相对较低。对于左转弯,最佳的前进比为0.25;对于右转弯,最佳的前进比为0.2。

图13 右转弯状态旋翼噪声辐射的地面声场

从图中可以看出,左转弯时噪声热点区域在Y轴正半轴地面区域;而对于右转弯,噪声热点在Y轴负半轴区域。对于噪声敏感区域,比如学校、养老院等,驾驶员可以选择一种转弯来有效降低对该类地区的影响。

3.2 固定观测点噪声分析

图14和图15分别给出的是左转弯、右转弯状态地面固定观测点声压级时间历程。从图中可以看出,对于同一类转弯,不同前进比下的同一观测点噪声级有所区别。对比图14(a)和图14(c)中的A观测点曲线,可以看出大部分时间前进比0.1对应的噪声级比前进比0.2状态高约7 dB。

图14 左转弯状态地面固定观测点声压级时间历程

对比相同转弯半径下的左、右转弯状态,可以看出不同的转弯方向会导致同一个观测点出现明显的噪声级差异。对比图14(d)和图15(d)中的C观测点曲线,可以看出在完成转弯动作的大部分时间右转弯噪声级比左转弯高8 dB以上。

图15 右转弯状态地面固定观测点声压级时间历程

4 结论

本文采用CAMRAD II/FW-H旋翼噪声快速分析模型计算了水平转弯状态的旋翼气动噪声特性,可得出以下结论:

1)随前飞速度增大,左/右转弯的辐射噪声级并不存在单调变化趋势,这与桨-涡干扰程度密切相关。

2)当转弯半径为40R时,左转弯状态最佳前进比为0.25,右转弯状态最佳前进比为0.2,通过合理地选择转弯前进比可以显著降低旋翼噪声。同时,应避免左转弯前进比0.1和右转弯前进比0.15这些桨-涡干扰强烈的飞行状态。

3)本文方法适用于工程计算分析,计算结果能够对直升机低噪声轨迹飞行提供有利指导,应用前景广阔。