基于机器学习的膝关节损伤检测方法

朱 俊

(安徽水利水电职业技术学院,安徽 合肥 231603)

膝关节对于人有着重要的作用,长期蹲着或者跪着的工人和长期训练的运动员膝关节都可能有损伤[1]。常见的膝关节损伤包括膝关节炎、软骨退化以及半月板损伤等。现有的医学诊断方法主要有MRI、CT图像、关节镜检查等[2]费用高昂,制约了对膝关节损伤的日常检测。Krishnan等人[3]通过加速度计采集了膝关节髌骨在运动中产生的振动信号,并依据此信号对膝关节不同类型的损伤进行检测。文献[4-6]对膝关节摆动信号的时频和非线性特征进行了分析,总结了利用不同信号特征进行损伤检测的方法。Befrui等人[7]提取了膝关节摆动信号的近似熵与包络幅度特征,并利用支持向量机等方法进行损伤分类。Nalband等人[8]在小波域提取了膝关节摆动信号的近似熵、样本熵等非线性特征,进行分类比较。这些方法通过提取膝关节摆动信号的特征,并采用对受损和健康信号进行分类。然而,信号受到噪声的影响,同时特征信息过多导致了信息冗余,限制了损伤检测的准确性。

1 检测方法

1.1 小波去噪

小波去噪是通过小波分解将信号变换到小波域,将模值较大的小波系数保留,同时将模值较小的小波系数去除,并根据保留的小波系数重构出原信号,达到信号去噪的目的。

假设观测信号如下:

f(t)=s(t)+n(t)

(1)

其中,s(t)表示信号部分,n(t)表示噪声部分,通常认为n(t)为高斯白噪声。采集得到的信号一般是离散信号,设f(t)的长度为T,即t=1,2,…,T,信号f(t)的小波变换为[9]:

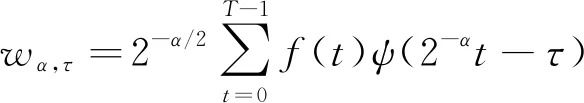
(2)

其中,α(α>0)表示尺度因子,τ表示平移量,wα,τ表示小波系数,Ψ(t)表示小波基函数,由此,对信号进行小波变换。在小波去噪中,对于变换得到的小波系数,采用阈值去除噪声。这里选取最小均方误差方法确定阈值,从而可以得到信号部分的小波系数,利用公式(3)将保留的系数重构原信号,即可实现信号的去噪,然后基于去噪后的信号,提取其特征。

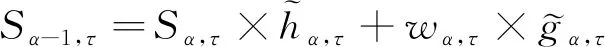
(3)

1.2 膝关节摆动信号的特征提取

小波变换可以提供信号在低频段的局部特征,但对高频部分的分辨率不足,难以获取精细的特征信息。膝关节摆动信号呈现出明显的非平稳性,其谱特性随着时间也在发生变化,因此,可利用小波包分解提取出不同尺度下信号的高频特征信息;此外,梅林倒谱系数能很好描述信号的静态特征,并对噪声具有一定的鲁棒性,将两种特征进行融合,可以有效区分不同的膝关节摆动信号。

1.2.1 小波包能量

小波分解在高频段分辨率较差,小波包分解能够克服这个不足,还可以描述信号的高频精细特征信息。通常,小波包分解可以用公式(4)表示[10]:

(4)

其中,h、g表示滤波器系数;d为小波包系数;k是小波包分解层数;j、n为小波包节点。通过上式,逐层进行分解,可以得到不同层数分解系数。假设信号f经过N层小波包分解,则f可表示为:

f=fN,0+fN,1+fN,2+…+fN,2N-2+fN,2N-1

(5)

其中,fN,0,fN,1,…fN,2N-2,fN,2N-1为信号经过N层小波包分解后的频带系数,对于经过N层小波包分解后的信号,则第j个频带中信号的小波包能量Ej计算如下:

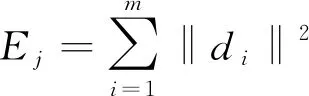
(6)

由此可计算出2j-1个小波包能量分量,这些分量分别包含了不同的信号特征信息。

1.2.2 梅林倒谱系数

梅林倒谱系数是将信号分别通过从低频到高频带内的一组带通滤波器,并将其映射到倒谱上得到的一组系数,反映了信号短时幅度谱特性,对噪声具有较强的鲁棒性。梅林倒谱系数的提取如图1所示。

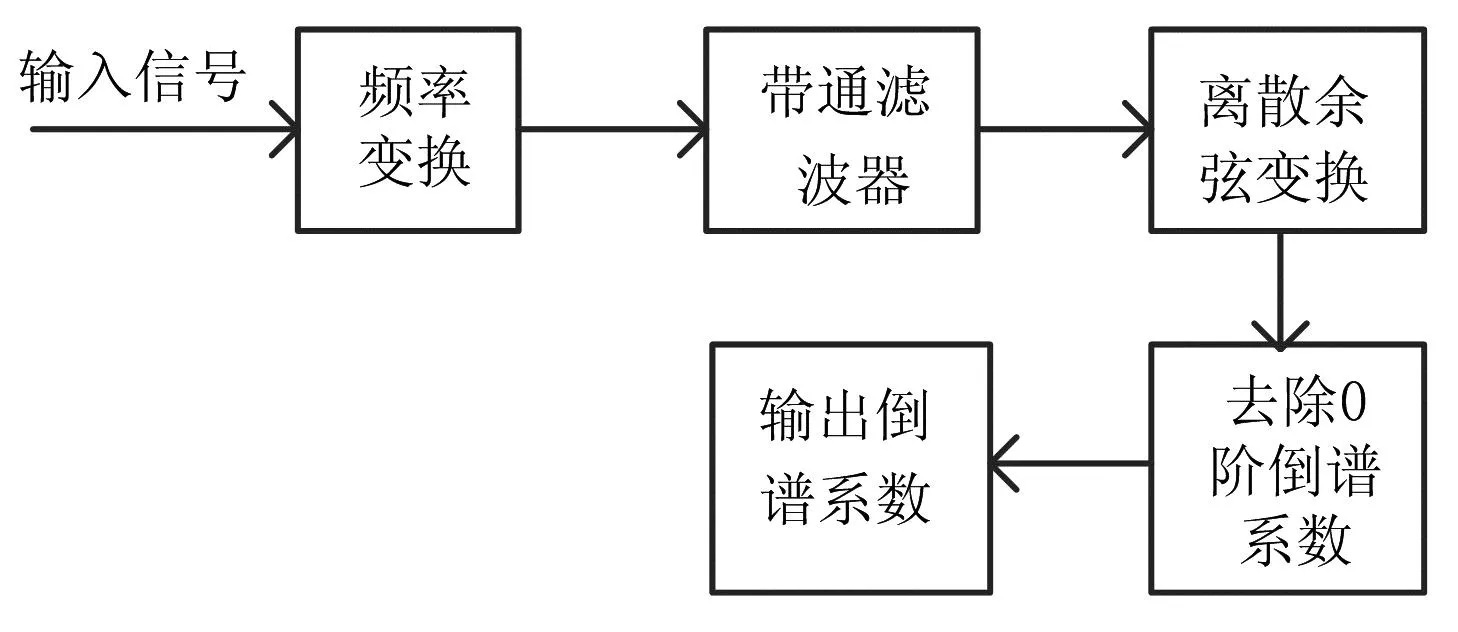
图1 梅林倒谱系数提取

具体提取步骤如下:

①对输入信号进行频域变换,常采用快速傅里叶变换;

②将频域信号通过M个带通滤波器,第m个带通滤波器函数可表示为:

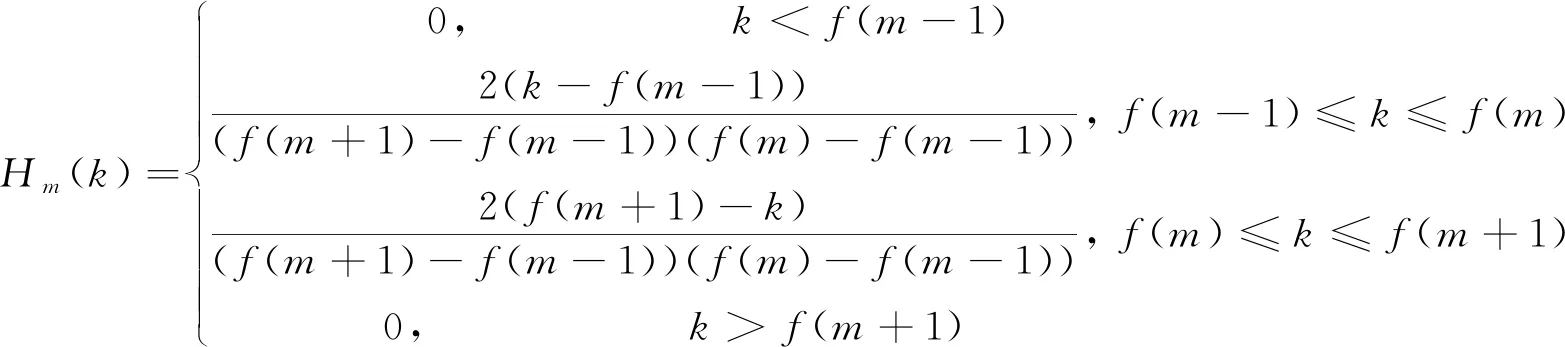
(7)

其中,f(m)为信号第m个频带的频率值;

③对滤波器的输出进行离散余弦变换,得到梅林倒谱系数[11],

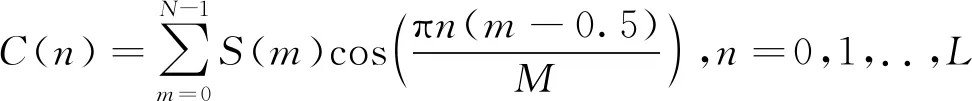
(8)

其中,C(n)为第n个梅林倒谱系数,S(m)是信号的对数梅林谱,L为梅林倒谱系数的阶数。通常,0阶倒谱系数表示频谱能量,主要包含噪声信息,一般需要舍弃;

④输出梅林倒谱系数向量,对于L阶倒谱系数,其系数向量可表示为:

K=[k1,k2,…,kL]

(9)

将信号的小波包能量特征与梅林倒谱系数进行融合,假设取第N层小波包分解后的小波包能量特征以及L阶倒谱系数,则信号的特征向量可表示为:

T=[EN,KL]=[E1,E2,…,E2N-1,k1,…,kL]

(10)

信号的特征向量T包含了信号的精细特性,可以有效地对不同类型的膝关节损伤进行检测。

1.3 膝关节损伤检测

通常,信号的特征向量T的维数较高,包含的特征信息较丰富,但同时也有较多的冗余信息,在进行分类之前,需采用主成分分析对向量T进行降维处理,以减少冗余信息,提升信号特征的区分性。然后,利用最小二乘支持向量机、径向基神经网络以及贝叶斯网络对膝关节摆动信号进行分类,区分不同类型的膝关节损伤,膝关节损伤检测方法如图2所示。

图2 膝关节损伤检测方法

2 实验结果与分析

2.1 数据采集

为了验证算法的有效性,本实验采集了318组数据,实验对象为安徽省霍邱县汇文学校341名学生。将加速度计捆绑于学生膝盖髌骨处,记录运动过程中的膝关节摆动数据,经过医学诊断对采集的数据进行分组,本次实验考虑到样本的多样性和覆盖面,样本空间的大小足够,避免了过度拟合和样本误差等问题。数据类型如表1所列。

表1 膝关节摆动信号类型

采集得到的数据341组,其中膝关节损伤数据212组,健康数据106组,由于记录误差较大或其他原因造成数据失效的数据23组,将有效的数据制作好标签分组存储好,以便于后续处理。

2.2 分类性能

在进行特征提取之前,需要去除信号里包含的噪声,图3给出了一组膝关节摆动信号的小波去噪结果。

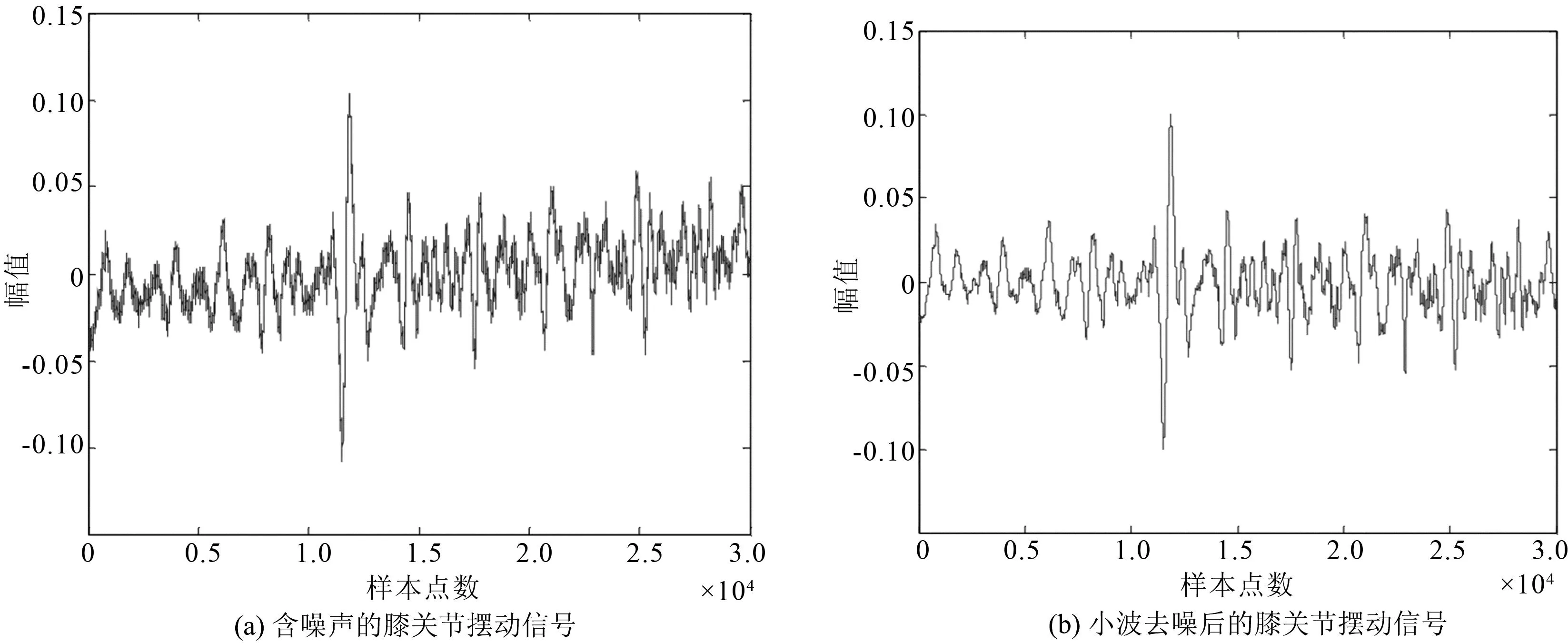
图3 膝关节摆动信号的小波去噪结果

从去噪结果可以看出,经小波去噪后,信号中的噪声部分遭到了削弱,信号变得光滑,更有利于特征信息的提取。

对于经过小波去噪的膝关节摆动信号,提取小波包能量特征与梅林倒谱系数特征,在实验中,基于第N=4层小波包分解计算每个子频带内小波包能量特征向量,向量有16维,同时,提取梅林倒谱系数L=16阶,经融合后,提取的向量维数为32。利用主成分分析对特征向量进行降维,取特征的维数为20。对每组膝关节数据经过小波去噪、特征提取、主成分分析降维,得到一个20维的特征向量,将此向量输入到分类器中,得出分类结果,计算正确分类概率。为了验证提出方法的优势,将分类结果与文献[7]和文献[8]的方法进行对比,如表2所列。

表2 不同方法的分类对比结果 %

从表2的结果可以看出,利用熵与包络幅度特征进行分类,采用最小二乘支持向量机可取得94.37%的正确分类概率,基于近似熵、样本熵特征进行分类,利用径向基神经网络可取得95.31%的正确分类概率,而利用本文提取的包络能量和梅林倒谱系数特征进行分类,通过径向基神经网络可获得96.58%的正确分类概率,因此,可以较好的验证本文方法的优势,利用本文方法可有效检测膝关节操作,避免反复重复单一动作的工人和运动员的膝关节操作进一步加重。

3 结束语

实验结果表明,基于小波包能量与梅林倒谱系数特征的正确分类概率优于熵与包络幅度特征、近似熵与样本熵的分类性能。未来的研究可进一步优化特征提取方式,以提高小波包能量与梅林倒谱系数特征在分类任务中的性能。