解答二面角问题常用的方法

陈金城

二面角问题侧重于考查二面角的定义、平面角的 定义、线面垂直的判定定理、三角函数的定义、正余弦 定理、勾股定理等知识的综合应用.求解二面角问题， 可以从向量、二面角的定义、垂直关系入手来寻找解 题的思路.下面结合实例来探讨解答二面角问题的几 种方法.

一、向量法

向量法是解答立体几何问题常用的一种方法.运 用向量法解答二面角问题，需先根据题目中立体几何 图形的特点，选择三条相互垂直的直线作为坐标轴， 建立空间直角坐标系；然后用空间坐标表示平面的法 向量；再根据向量的夹角公式来计算两个法向量的夹 角，则所求的夹角或其补角，即为二面角.

例1

解：

解答本题，首先要根据直四棱柱 ABCD - A1B1C1D1 的特征：侧棱垂直于底面，来建立空间直角坐标系；然 后根据线面垂直的判定定理求平面 AMA1 、平面 DMA1 的法向量；最后根據向量的夹角公式 cos < n，m >= n?m |n|?|m| ， 求得问题的答案.

二、定义法

一般地，我们用二面角的平面角来表示二面角的 大小，因此求二面角的关键是根据二面角的平面角的 定义来解题.首先要确定二面角的棱；然后在棱上任取 一点，过该点在两个半平面内作棱的垂线，则这两条 垂线的夹角即为二面角的平面角.利用定义法，可将二 面角问题转化为平面角问题，利用正余弦定理、勾股 定理、三角函数的定义即可解题.

例2

解：

我 们 先 根 据 等 腰 三 角 形 中 线 的 性 质 判 定 AE ⊥ BC，DE ⊥ BC ，即可根据二面角的平面角的定义，确定二面角 A - BC - D的平面角为∠AED；然后在ΔAED 中，根据余弦定理求得二面角的平面角的余弦值.

三、三垂线法

用三垂线法求二面角的关键是作三垂线，以此来 确定二面角的平面角.在解题时，需先在一个半平面内 选取一点；然后过此点向另一半平面内作垂线；再由 垂足向二面角的棱作垂线，即可作出二面角的平面 角；最后根据勾股定理、正余弦定理求平面角的大小.

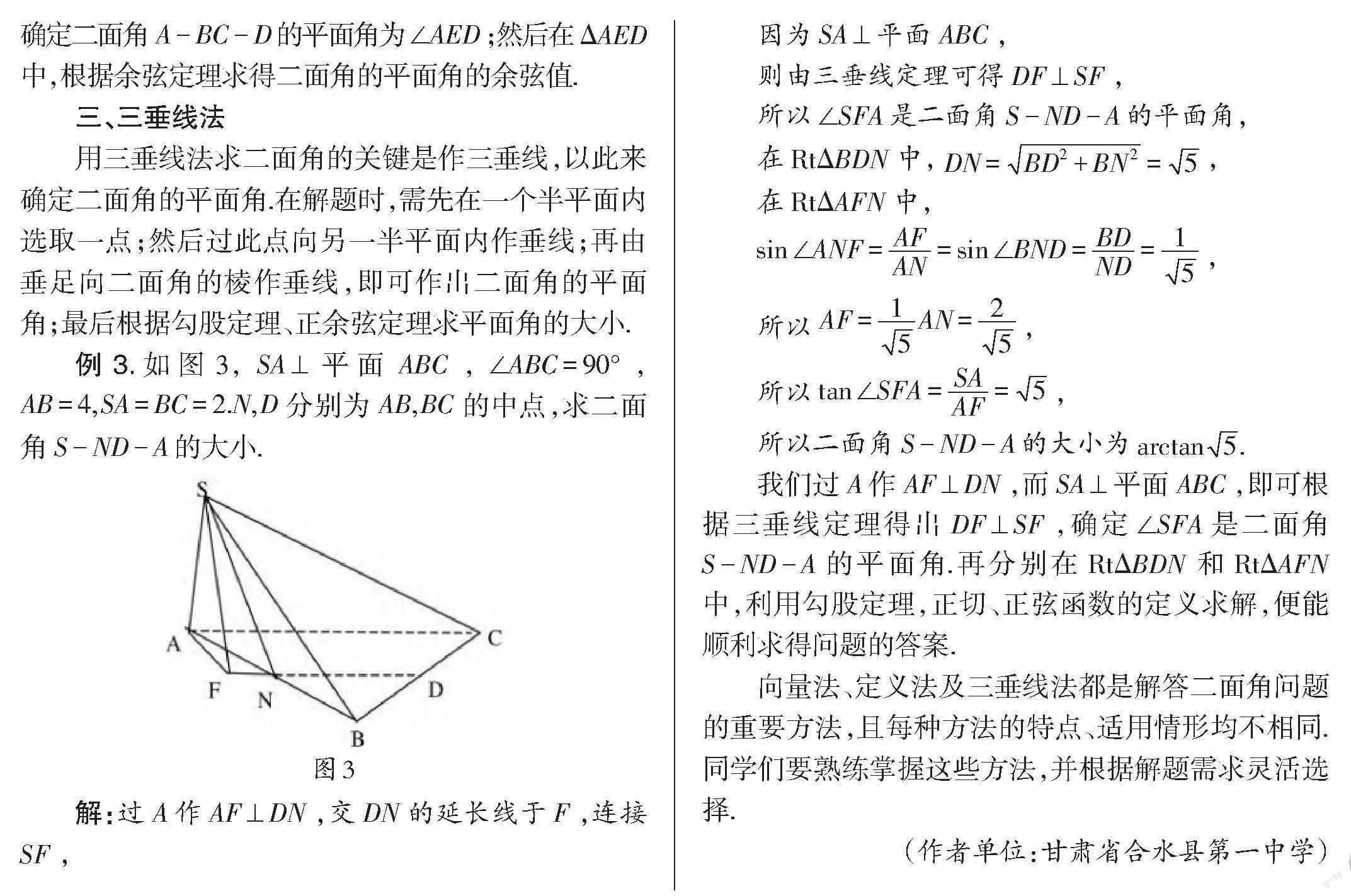
例3

解：

我们过 A 作 AF ⊥ DN ，而 SA ⊥ 平面 ABC ，即可根 据三垂线定理得出 DF ⊥ SF ，确定 ∠SFA 是二面角 S - ND - A 的平面角.再分别在 RtΔBDN 和 RtΔAFN 中，利用勾股定理，正切、正弦函数的定义求解，便能 顺利求得问题的答案.

向量法、定义法及三垂线法都是解答二面角问题 的重要方法，且每种方法的特点、适用情形均不相同. 同学们要熟练掌握这些方法，并根据解题需求灵活选 择.

（作者单位：甘肃省合水县第一中学）