隧道围岩稳定性及岩爆段快速施工研究
赵 岩
(中铁十二局集团有限公司,山西 太原 030000)
0 引言
隧道工程施工中不可避免地会穿越不良地质体,例如岩溶、软弱围岩和岩爆地层,在这些地层中施工掘进、爆破震动产生的扰动以及施工开挖卸荷效应会使开挖后的隧道围岩极易出现松动、坍塌和应力集中现象,在深埋隧道和高地应力地段的地层中则更易发生岩爆,围岩的应力也以岩爆释放的方式达到新的岩体应力调整和平衡[1]。岩爆事故随着岩体的破裂、爆裂和弹射,进而会引发大规模的隧道围岩坍塌,这对隧道工程安全而言是极为重大的挑战,因此有必要对高围压地应力段的隧道围岩稳定性进行研究,并提出一种行之有效和快速安全的施工工法,以提高隧道工程施工的工程效益[2]。
1 工程概况
新建铁路广州至湛江高速铁路工程大脊山隧道位于广东省云浮市新兴县境内,进口里程为DK137+035,进口为缓坡,横坡坡度10°~20°,出口里程为DK146+641,出口为缓坡,横坡坡度20°~30°,坡面大量分布风化残留孤石,隧道场区为中山地貌,地表起伏较大,相对高差850m左右,隧道最大埋深约648m,隧道进出、口出覆盖层较厚,区内植被发育,多为灌木林,覆盖面积100%。
场区覆盖层为第四系全新统坡洪积层(Q4dl+pl)、残破积层(Q4dl+el)、下伏基岩为燕山早期黑云母花岗岩(γ52(3)c),其中坡洪积层主要为③-3 软塑状粉质黏土,厚度约1~8m,属II 级普通土;坡残积层主要为粉质黏土,主要分布于山体斜坡上,属II 级普通土;⑨-1 花岗岩厚度约40m,属于IV 级软岩石,由于差异风化,因此中间见多层0.5m~2.0m厚的强风化及弱风化层,其总厚度为10m~30m,弱风化带属V 级次坚石。
该隧道埋深较大处为燕山期(γ52(3)c)黑云母花岗岩,DK140+020~DK141+010 段埋深大于500m,最大埋深651m,地应力较高,有发生岩爆的可能,采用应力比法测试结果见表1。统计表明,隧道最大埋深段岩体饱和单轴抗压强度Rc=74.1MPa,最大主应力σmax=12.7MPa,Rc/σmax=5.83。根据区域地质构造,该隧道最大埋深处位于腰岗断裂和高溪断裂之间,位于断层抬长升盘,其应力较为集中,发生岩爆的可能性较大,施工时应对可能发生岩爆的地段采取超前钻探后喷雾洒水等处理方法[3]。

表1 隧道洞身范围内岩爆段花岗岩饱和单轴抗压强度测试成果
2 高地应力条件下隧道围岩稳定性分析
2.1 高地应力条件下隧道围岩稳定性理论分析
在现有高地应力易发岩爆的隧道围岩稳定性理论分析中,通常通过太沙基理论和普氏理论对掌子面的地应力进行分析,研究围岩压力的演变过程以判别是否发生岩爆灾害。太沙基理论的围岩压力计算方法如公式(1)、公式(2)所示[4]。
式中:σv为围岩发生临界失稳时支护结构对拱顶的支撑压力,当σv>0 时,围岩拱顶将发生失稳,当σv≤0 时,围岩拱顶基本稳定;σh为围岩发生临界失稳时支护结构对拱腰的支撑压力,当σh>0 时,围岩拱腰将发生失稳,当σh≤0 时,围岩拱腰基本稳定;b为围岩的发生失稳时的跨度;γ为围岩的容重;c为围岩体的等效黏聚力;φ为围岩的等效内摩擦角;z为隧道的埋深;λ为隧道的侧向压力系数;h为隧道拱高;H为等效围岩自重计算高度。
普氏理论的围岩压力计算方法如公式(3)、公式(4)所示。
式中:q为隧道拱顶的压力;f为普氏系数;a为矢跨半径,a=a1+Htan(45°+φ/2);R为隧道半径,其余参数定义如公式(1)和公式(2)。
分别采用普氏理论和太沙基理论对隧道掌子面DK140+135 位置处的拱顶压力和隧道侧壁压力进行计算,并考虑侧向压力系数和普氏系数对围岩压力的影响,计算结果见表2。

表2 不同理论计算的隧道拱顶围岩压力和拱腰围岩压力
从表2 可以看出,随着侧向压力系数λ的增加,基于太沙基理论计算的隧道拱顶压力和拱腰压力均不断降低,侧向压力系数λ从0.30 增至0.60 时,拱顶压力546.61kPa 降至312.38kPa,降低幅度为42.85%,而拱腰压力从122.05kPa 降低到了680.93kPa,降低幅度为44.22%。同样地,采用普氏理论计算的结果表明,随着普氏系数f 的增加,得到的隧道拱顶压力和拱腰压力均呈现不断降低的趋势,普氏系数从10 增加到22 时,拱顶压力从459.96kPa 降至297.01kPa,降低幅度为35.43%,拱腰压力从1141.43kPa 降低到了977.04kPa,降低幅度为14.40%。从表2 还可以看出,无论是采用太沙基理论还是采用普氏理论计算围岩压力,所得到的拱顶压力和拱腰压力均大于零,表明隧道的围岩处于不稳定状态。对比太沙基理论计算结果和普氏理论计算结果可知,采用普氏理论得到的隧道拱顶压力和拱腰压力均略小于采用太沙基理论得到的隧道拱顶压力和拱腰压力,综合表明太沙基理论对高地应力段隧道围岩稳定性的判断更为保守,而普氏理论在评价的适用性以及工程的经济性方面具有更好的工程价值。
2.2 基于现场实测数据的高地应力条件下隧道围岩稳定性分析
为了研究隧道在高地应力条件下隧道围岩的稳定性,沿着隧道圆形边界不同位置布置应力监测点和位移监测点,应力值的监测设备为锚杆应力计,而位移收敛值的监测设备为钢弦式位移计,以观测隧道施工开挖过程中掌子面的应力应变时空演变过程。
在里程DK140+135 和DK138+980 这2 个断面进行隧道的地应力和变形测试,结果如表3、图1 和图2 所示。

表3 不同里程段隧道断面的围岩压力和位移监测结果

图1 不同里程段隧道的围岩位移监测结果

图2 不同里程段隧道的围岩压力监测结果
由图1 可以看出,位于高地应力处DK140+135 断面的拱顶压力、拱腰压力变化规律均与非高应力段DK138+980断面的拱顶压力、拱腰压力变化规律有显著不同。随着监测时间的增加,位于高地应力处DK140+135 断面的拱顶压力和拱腰压力不断增加,并没有出现收敛的迹象,拱顶压力最大达到4.29MPa,拱腰压力最大达到8.00MPa,因此围岩的稳定性较差,极易诱发岩爆。而位于非高地应力段DK140+135 断面的拱顶压力、拱腰压力变化规律则呈现明显的非线性变形,尽管变形的增长速率较慢,但随着监测时间的增加,拱顶压力和拱顶压力均逐步趋于稳定和收敛且小于DK140+135 断面相应位置的拱顶压力和拱腰压力,拱顶收敛压力为2.52MPa,拱腰收敛压力为2.73MPa,表明该段断面的围岩处于较稳定的状态。
由图2 可以看出,位于高地应力处DK140+135 断面的拱顶位移、拱腰位移变化规律均与非高应力段DK138+980断面的拱顶位移、拱腰位移变化规律有显著不同。随着监测时间的增加,位于高地应力处DK140+135 断面的拱顶位移和拱腰位移呈现一定程度的缓急增加状态,并没有出现位移收敛的迹象,拱顶最大位移为108.38mm,拱腰最大位移为93.13mm,因此围岩的稳定性较差,极易诱发岩爆。而位于非高地应力段DK140+135 断面的拱顶压力、拱腰压力变化规律则呈现明显的非线性变形,尽管变形的增长速率较慢,但随着监测时间的增加,拱顶位移和位移均逐步趋于稳定和收敛且远小于DK140+135 断面相应位置的拱顶位移和拱腰位移,拱顶收敛位移为44.67mm,拱腰收敛位移为33.05mm,表明该段断面的围岩处于较稳定状态。
3 岩爆段落隧道快速施工方法
为了快速安全地穿越高地应力的岩爆地段,需要采取快速有效的施工掘进方法以降低隧道的围岩压力。该文针对隧道的施工过程的总结表面,提出隧道快速施工工艺,如图3 所示。实践表明,采用隧道快速施工工艺后,每延米隧洞施工平均耗费时间约135min,与理论施工耗时505min相比,节约时间370min,大大节约了施工工期。
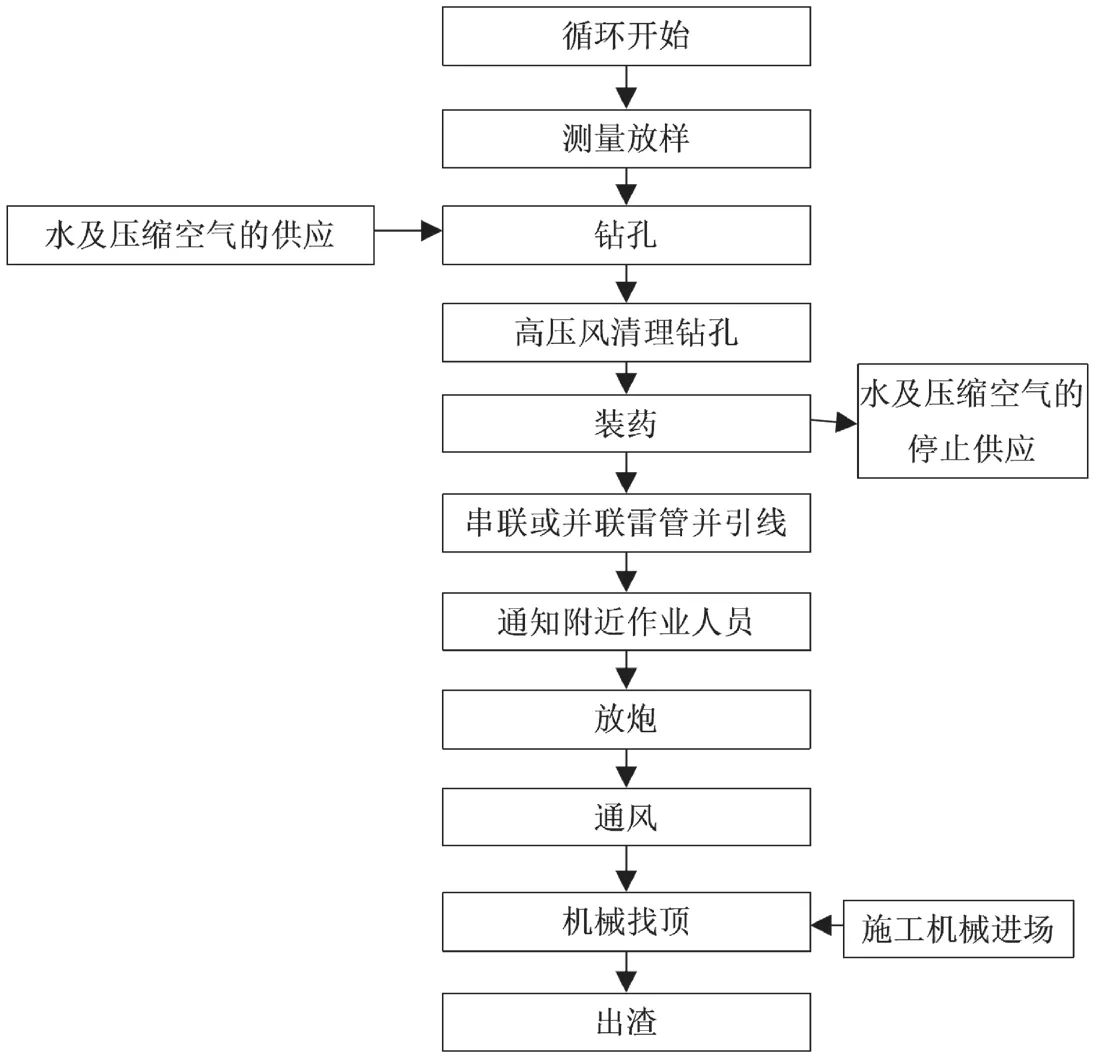
图3 穿越高地应力的岩爆地段隧道施工工艺
4 结语
该文以新建铁路广州至湛江高速铁路工程大脊山隧道为研究对象,在分析隧道的工程地质条件基础上,采用理论分析和现场实测的手段对隧道掌子面不同位置处的围岩应力和位移进行分析,并提出了岩爆段快速施工方法,得出以下结论:
高地应力处DK140+135 断面计算表明,无论是采用太沙基理论还是采用普氏理论计算围岩压力,所得到的拱顶压力和拱腰压力均大于零,表明隧道的围岩处于不稳定状态。对比太沙基理论计算结果和普氏理论计算结果可以知道,采用普氏理论得到的隧道拱顶压力和拱腰压力均略小于采用太沙基理论得到的隧道拱顶压力和拱腰压力,综合表明太沙基理论对高地应力段隧道围岩稳定性的判断更为保守。
位于高地应力处DK140+135 断面的围岩压力和围岩变形变化规律均与非高应力段DK138+980 断面的围岩压力和围岩变形变化规律有显著不同,DK140+135断面的围岩压力和围岩变形无收敛现象,围岩不稳定;DK138+980断面的围岩压力和围岩变形出现稳定和收敛现象,围岩稳定。
实践表明,采用隧道快速施工工艺后,每延米隧洞施工平均耗费时间约135min,与理论施工耗时505min 相比,节约时间370min,大大节约了施工工期。

