基于机理分析指导的煤质水分神经网络软测量

何志明 赵蕴宏 赵宗辉 王德庆 赵太磊

（1.国家电投集团内蒙古白音华煤电有限公司坑口发电分公司，内蒙古 锡林郭勒盟 026208；2.国家能源集团湖南永州公司，湖南 永州 425000）

0 引言

煤的水分含量高会增加燃烧需要的热量，不利于煤粉的充分燃烧，从而导致飞灰含碳量升高[1]。因此，获得准确的煤质水分含量，匹配与之对应的干燥风流量就可以降低煤粉的含水量，对提高电厂的经济效益有重要意义。煤质在线检测仪器价格昂贵、应用要求高且后期维护投入大[2]，很少有电厂配备煤质在线检测装置。常规的理论计算方法准确性和可靠度高，但是其原理复杂、计算量大，很难满足煤质水分含量实时监测的要求。利用神经网络等机器学习算法建立的软测量模型的结构相对简单且计算速度快，能够满足现场使用的需求。因此，该文提出了一种基于机理分析指导的煤质水分神经网络软测量方法，该方法通过机理建模法分析将软测量的辅助变量作为神经网络的输入参数，以建立煤质水分的神经网络模型，从而提高煤质水分软测量的可靠性。

1 建立煤质水分机理模型

目前，已有很多基于机器学习算法的软测量实例，金秀章等[3]提出了一种基于KPCA 和LSSVM 的锅炉飞灰含碳量软测量方法，该方法通过KPCA 算法选取飞灰含碳量相关的辅助变量，以此作为LSSVM 飞灰含碳量软测量模型的输入，从而提高模型的精度。冯旭刚等[4]提出了一种基于遗传神经网络敏感度分析的飞灰含碳量测量方法，该方法通过Grason 敏感性分析算法筛选飞灰含碳量的输入参数，并采用遗传算法优化连接权值、阈值和隐层节点个数，以提高网络的泛化能力。文献[5]提出了一种基于粒子群优化的RBF 神经网络算法来建立锅炉燃烧优化控制模型，利用专家经验人为给定模型的输入参数。现阶段，国内学者多数采用主成分分析法等数理统计方法或根据经验直接人为确定软测量模型的输入参数，主成分分析法基于数理统计的原理，无法确保规避物理性错误，而人为经验法本身的可靠性难以衡量，因此该文提出了一种基于机理分析指导的煤质水分神经网络软测量方法，该方法通过机理建模法建立煤质水分的模型，选取机理模型中的变量作为神经网络的输入参数，以建立煤质水分的神经网络模型，从而提高煤质水分软测量的可靠性。

机理建模是根据系统的机理建立系统模型的过程，一般需要充分了解系统的工艺流程及其涉及的物理化学变化，常见的机理建模方法主要基于质量守恒定理、能量守恒定理、传热学以及化学反应物质守恒等原理。赵征等[6]针对建立煤质参数机理模型提出了一套较完整的方法，其基本思想是利用能量守恒原理，对制粉系统来说，进入制粉系统的总能量应等于系统消耗的能量与带出系统能量的和，笔者参考该方法并修正部分细节上的瑕疵，从而建立煤质水分的机理模型，具体步骤如下。

1 kg 原煤经过制粉系统研磨，输入制粉系统的总能量qin（kJ/kg）应等于被消耗及带出的总热量qout（kJ/kg），据此建立能力守恒方程，如公式（1）~公式（3）所示。

式中：qag1为干燥剂的物理热；qrc为原煤物理热；qmac为磨煤机研磨煤粉所产生的热量；qs为密封风的物理热；qle为漏入冷风的物理热；qev为原煤中水分被蒸发所吸收的热量；qag2为乏气带出的热量；qf为加热燃料消耗的热量；q5为设备散热损失。

将公式（1）、公式（2）带入公式（3），就可以得到公式（4）。

其中，qrc、qev以及qf3 个变量的计算式中都包括煤水分Mar，将这3 项移到等式一边，就可以得到公式（5）。

求解这个关于煤质水分Mar的一元二次方程，其中有实际意义的实根即为入炉煤的水分含量。

2 基于机理分析指导的神经网络模型

2.1 神经网络模型与机理模型指导

BP 神经网络是一种基于误差逆向传播训练的网络算法，也是目前发展最成熟、应用最广泛的神经网络模型[7]，常被用于非线性建模、模式识别、系统辨识、结果预测和控制等领域。

BP 神经网络的BP 是误差反向传播算法（Error Back Propagation Training）的缩写。提到BP 神经网络就不得不提到在人工神经网络发展中起到启发作用的感知机（Multilayer Perceptron，MLP）网络，单层感知网络模型（M-P）最早被作为一种神经网络模型，它具有模型清晰、结构简单以及计算量小等优点，这些优异的性能引发了人们研究人工神经网络的热潮。但是，随着对单层感知机网络的深入研究，人们发现它还存在许多不足，最致命的就是它无法处理非线性问题，而实际应用中90%都是非线性问题，这使它的应用价值降低。随后，研究者们采用复杂的非线性函数取代计算单元中的阀函数，然而这样也无法突破算法只能解决线性可分问题的局限。

提高感知机模型的分类和识别能力（以解决非线性问题）的唯一方法就是改变初始的单层结构，通过构建多层感知机模型来反映非线性，在输入层和输出层之间添加多层前馈网络来构成多层前馈感知器网络模型，它就是BP神经网络的雏形。在BP 神经网络模型中，输入层与输出层之间的部分被称为隐含层。

从算法本质上来说，BP 算法以网络误差平方最小为目标，使用梯度下降法来求解各连接层间的权重系数。在结构上，BP 神经网络最终确定了输入层-隐含层-输出层的基本结构。BP 神经网络算法解决了简单感知器不能解决非线性问题的致命缺陷。

BP 神经网络的输入就是软测量模型要选取的辅助变量，常规的辅助变量选取通常采用主成分分析法等数理统计方法，但是纯数理统计方法只根据数据离差平方或方差来判断、选取辅助变量，这就有可能导致2 种致命缺陷：1） 当样本规模不够大时，难以避免出现因偶然相关性而误选变量的情况。2） 由于缺少机理的分析，因此可能导致选择的相关辅助变量与待测变量因果关系倒置。这2 种情况都会降低软测量模型的可靠性。

综上所述，该文提出的基于机理分析指导的煤质水分神经网络模型的机理分析指导分为选取变量和生成数据2个方面：1） 上文在使用能量守恒构建煤质水分机理模型的过程中涉及的物理变量共6 个，分别为磨煤机入口一次风温度t1、磨煤机一次风量Q1、磨煤机给煤量m1、磨煤机电流I、磨煤机出口风粉混合物温度t2以及在煤需要解冻时还要考虑的环境温度t3min。因为整个环节涉及的变量维数不高，所以没有降维的需求，因此直接根据机理指导机器学习建模的思想，将这6 个量选为建立软测量模型的辅助变量，即神经网络的输入变量，神经网络的输出为煤质水分。2） 大部分电厂不具备在线的煤质检测装备，而煤质信息通常需要由化验分析得出，定期的化验数据只能给出离散的检测结果，这就导致煤质水分没有连续的实时值数据，因此，所建立的机理模型的另一重要功能便是通过机理计算生成煤质水分的连续输出序列，为训练神经网络模型提供数据。

采用BP 神经网络建立煤质水分的机器学习软测量模型，需要确定神经网络的结构，输入节点数为选取的辅助变量维度（即为6）。输出节点是软测量模型的输出，该模型仅输出煤质水分，因此维度为1。隐含层的结构及神经元数量是影响BP 神经网络模型效果的主要因素，理论上网络隐含层的神经元越多，模型的精度就越高，但是神经元个数过多就会导致模型的训练时间延长，还可能导致出现过拟合的情况，因此通过需要多次试验来确定隐含层的合理结构。

2.2 仿真分析

根据国内某电厂提供的数据进行机理分析指导法的仿真。根据电厂运行规程，设定机理模型中的固定参数，包括磨煤机设计出力、煤粉细度以及干煤比热容等（该电厂主要使用褐煤，设定干煤比热容为0.933 kJ/(kg·K)）。

采集该电厂2021 年5 月第一周的运行数据进行仿真试验，采样间隔为60 s，共计10 080条数据。数据采集的测点包括锅炉侧热一次风温度t-1、磨煤机一次风流量Q1、磨煤机磨煤量m1、磨煤机电流I、磨煤机出口风粉混合物温度t-2以及环境温度t-3min。

采用拉依达法则异常值检测算法去除异常数据后，将数据输入机理模型，通过机理模型的计算得到煤质水分含量数据序列。将机理模型计算的结果与电厂实际化验结果进行对比，两者存在一定误差，机理模型对干煤比热容等参数上使用的统计数据、设计数据以及部分过程进行了简化，因此存在误差，但是本身的计算原理还是可靠的，为了使机理模型计算结果符合现实情况，考虑通过添加修正系数α来修正机理模型计算结果。修正系数α的具体确定过程如下：1） 以机组化验数据为煤质水分的参考基准（该段数据化验值为29.18）。2） 机理计算的结果总体偏小，大致确定修正系数α为1~2。3） 采用粒子群智能寻优算法寻找最优的修正系数α。4） 将寻优函数Q设为整体数据与化验值的均方误差，如公式（6）所示。5） 在论域1~2 中寻找使Q最小的α，即为最佳修正系数。

式中：Q为寻优函数；Mari为第i个由机理模型计算出的煤质水分；Marhy为煤质水分化验数据值；n为数据长度，即机理模型输出的结果个数。

最终求得的最佳修正α为1.399，平均偏差约为1.51%，换算到相对偏差为5.19%（以29.18 为基准），精度可以满足电厂在生产中的使用要求。

将上述修正后的煤质水分序列作为神经网络训练的输出序列。根据经验可以确定神经网络结构为具有2 层隐含层的BP 神经网络，激活函数采用ReLU 函数；神经网络的输入同机理模型（6 维），输出是煤质水分（1 维），接着需要确定2 层隐含层的节点个数，为了提高试验速率，先取前1 000 组输入/输出数据进行测试性试验。经过多次试验，初步确定当第一层隐含层节点数为5、第二层隐含层节点为2 时，网络效果较好。当第一层隐含层节点数为5、第二层隐含层节点为3 时，网络效果较好，在输入全部数据后发现，神经网络输出曲线总体与原始曲线可以较好地贴合，但是在极值位置处，预测能力明显下降，网络结构仍有进一步优化的空间，经过反复调整试验，最终将网络结构确定为6-5-3-1，即第一隐含层5 个神经元，第二隐含层3 个神经元（比之前增加了1个神经元），其预测输出与原输出对比结果如图1 所示。由图1 可知，网络的预测能力优秀（平均绝对值误差为0.033 4），存储网络结构和参数，后续进行煤质水分预测时直接调用即可。

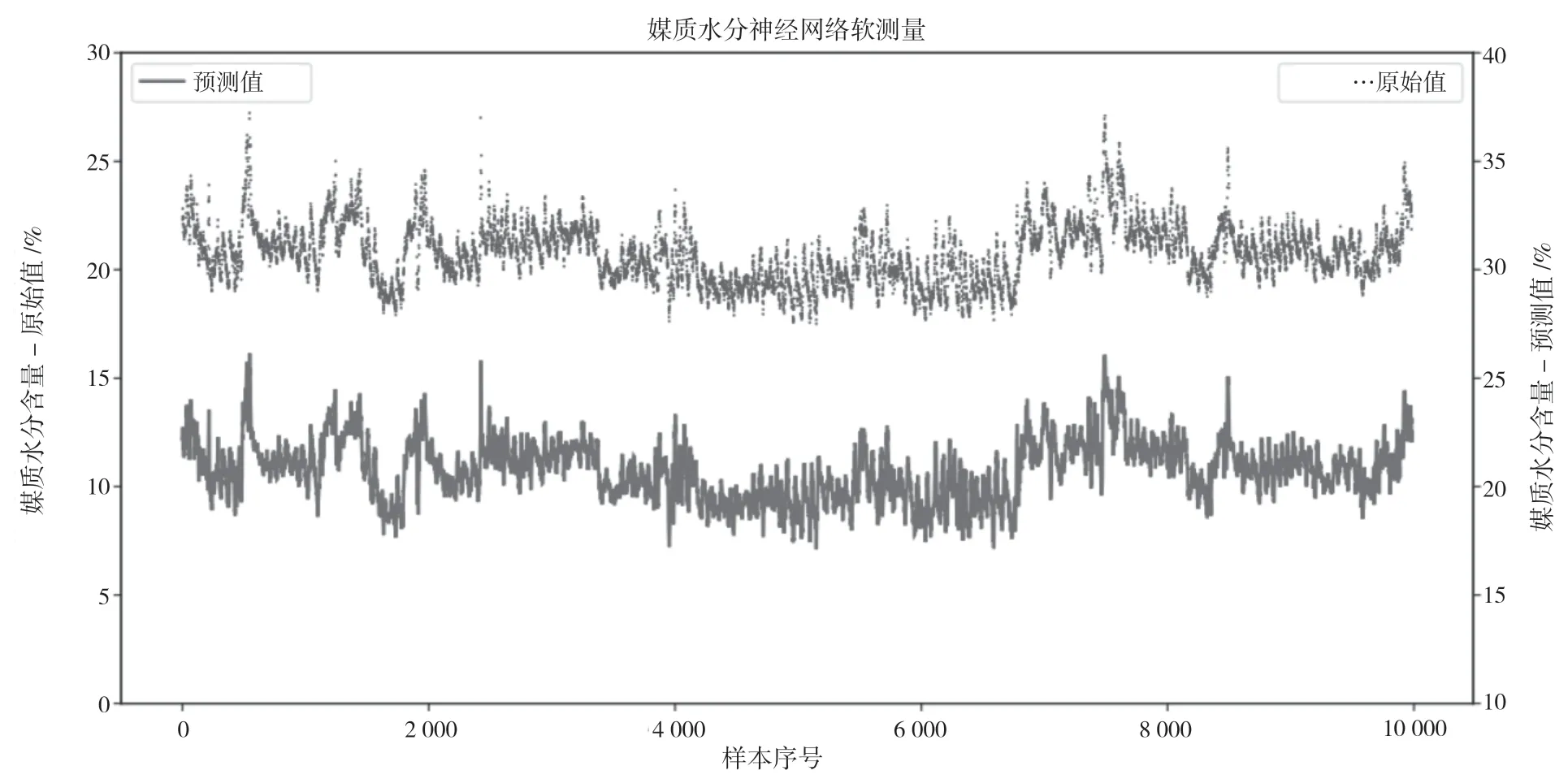
图1 神经网络输出与原始输出对比（9 983 点，网络结构6-5-3-1）

需要说明的是，由能量平衡建立的关系模型为静态平衡关系，当机组大范围变出力时，由于制粉系统存在惯性，因此会造成入口和出口的测量数据存在暂时不匹配的现象，从而导致计算结果出现异常[8]。笔者提出的基于机理分析指导的煤质水分神经网络软测量方法以能量平衡计算结果为基础，因此仅适用于静态平衡关系的预测，如果要使网络预测适用于动态过程，还须对该方法进行改进。

3 结语

该文提出了一种基于机理分析指导的煤质水分神经网络软测量模型建立方法，其核心是根据机理模型建立的原理选取神经网络的输入参数，并利用机理模型生成连续数据供神经网络训练，以解决现场无法给出煤质水分连续测量数据的问题。与主成分分析法等基于数理统计的参数选取方法相比，机理指导法以物理原理作为支撑，能够规避变量选择中的原理性错误，具有一定的优势。当然，在机理指导筛选后，仍然存在参数维数很高的情况，可以进一步使用数理统计方法进行降维，后续可以在这方面进行深入研究。同时，该文提出的机理指导法为不易实时测量但物理规律明确的参数软测量提供了一种普遍性思路。