模糊分析法对电厂安全性评价的优化
王凤芹
(国家能源集团国源电力有限公司,北京 100033)
智能算法通过构建集合[1]、相似度、插值等方式[2],获得电厂安全性数据[2],并对数据进行标准化处理,降低数据的复杂度[3]、剔除无关属性,形成电厂安全性数据集合[3]。同时,智能算法能减少电厂安全性分析的数据量[4],实现对电厂的实时监测,并深入挖掘安全隐患出现的原因[5]。另外,智能算法能主动进行安全性分析[6],对安全风险数据进行插值,实现电厂的持续性监测[7]。智能算法对不同监测点的仿真分析,计算信息的安全性[8]、数据异常性以及时滞性等[9]。智能算法对各时间点的信息量、信息复杂度进行分析,并记录分析结果,能够减少冗余信息量,验证信息的时滞性,加强对电网、潮流、电压等指标监测,为电厂预警奠定基础。但是,以往的算法无法处理海量数据,不能进行实时监测,而且占用大量的系统资源。因此,寻找一种有效的安全性评估方法,是电厂安全分析需要解决的问题。有学者提出将模糊理论应用到电厂安全性评估中,该方法不仅能减少数据处理的流程,而且通过模糊分析理论对安全性评价进行高效评估,以提高电厂安全性的评估效果。由此,该文以电厂安全性数据为基础,利用模糊分析方法的优势,进行电厂安全性仿真评估,旨在提高电厂安全水平。
1 电厂安全性评价的数学描述
为了更好地进行电厂安全仿真评估,需要对相关数据进行数学描述,并引入安全性评估函数。电厂安全评价分析主要包括安全性评价内容、安全性预警描述以及安全因子的调节设置等,具体内容如下。
1.1 电厂安全性描述
假设A:监测点为xi,i值为监测点所处的设备,分别为发电设备=1,传输设备=2,储能设备=3,管理设备=4,预警设备=5,...,等记录;j值为设备信息发送原因,分别为持续性差=1,数据丢失=2,超出阈值=3,…,等原因。电厂的安全性评估结果为yj,j值为评估方式,分别为单指标评估=1,多指标评估=2,跨设备评估=3,整体评估=4,预警为zk,k值为预警方式,分别为局部预警=1,整体预警=2。安全性评估函数为H(x,y,z|p),计算过程如公式(1)所示。
式中:choice{}为安全性计算函数,对电厂安全性进行综合评价;p为安全性预警约束。
1.2 安全性预警描述
假设2:预警状况为Di,数据完整程度为Oi,安全性评价指标为Oi。其中,i值为预警等级,分别为I 级=1、II级=2、III 级=3,…等。在电厂安全性评价中,安全性与预警原因之间的关系为rei,分别为独立=1、相关=2、显著相关=3,…等。在安全性标准一定的情况下,其各设备的安全系数也是固定的,所以设置设备安全性标准为Bi,设备出现故障概率为pi,计算过程如公式(2)所示。
其中,Bi相对固定,与设备发生故障的概率,安全等级相关。利用模糊分析法对电厂设备进行监控,测试设备的运行性能以及设备出现异常数据量,并将相关信息存入日志中。
1.3 安全调节因子的描述
安全调节因子是评价的关键,所以要引入安全调节因子。安全因子要协调不同指标和不同参数之间的关系,调节参数之间的影响程度,来保证安全调节因子分析的准确性。同时,要对安全调节因子的指标进行深入判断,确定不同参数之间的关系,保证参数的独立性,以此来保证后期分析的准确。假设3:将安全阈值为A,发送设备为Aa,预警信息为Ba,安全调节函数为T(Aa,Ba|A),安全调节因子的计算如公式(3)所示。
1.4 安全互动因子的描述
安全互动因子是不同指标、不同设备之间的互动因子分析,主要是保证电厂安全性能的分析有效性,可以对电厂安全性能进行综合性的评价,从全局的角度分析相关的数据和指标变化。安全互动因子是电厂安全性能评价中的重要内容,也是电厂安全综合评价结果的重要指标。在电厂设备正常运行情况下,监测信息与反馈信息为1 ∶1 的关系,安全互动信息相等,安全率一定,而且安全系数随设备不同而不同。由于安全系数相对固定,因此互动因子发送的设备信息相互独立,可以进行独立分析。安全互动因子一旦出现差值,电厂设备存在一定风险,需要进一步进行安全信息挖掘。假设4:互动差值为ΔAa,安全性评价时间为T,双向安全阈值为dt,那么安全互动函数为TH(ΔAa|At),计算过程如公式(4)所示。
其中,在安全阈值一定的情况下,互动差值越小,安全性越高。同时,利用模糊分析法对电厂安全性数据进行标准化处理,并挖掘所有信息数据,判断是否达到预警要求。然后,对预警信息进行验证,进行安全互动。
1.5 电厂安全性综合评估
结合上述分析,对电厂安全性进行综合评价,从电厂角度筛查异常信息,并对异常信息进行挖掘,找出异常信息出现的原因。假设5:不确定性干扰发生概率为ξ,电厂设备出现安全性问题的概率为pv,电厂负荷为Lod、安全信息的稳定性为Wd,安全等级为gri,电厂安全性综合评估函数为Zon(di),其计算过程如公式(5)所示。
2 110 kV 电厂安全性评价案例
2.1 110 kV 电厂安全性概述
电厂安全性评价指标包括电压、电流、功率、潮流以及相关数据的正态性。当电厂设备出现异常值时,相关指标将会出现较大波动,而且大于相应阈值。采用模糊分析法对电厂设备数据进行监测,对部分不完整信息,通过模糊插入方法进行补充,具体参数见表1。
根据表1 中的数据可知,电压、电流和功率等安全指标参数在不同阶段、不同模糊程度的要求下,均未出现大幅度的变化,说明各数据之间无显著性的差异,可以进行后期的进一步分析。虽然处理阶段、模糊程度等算法存在小幅度的变化,但是变化幅值相对较小,统计学分析显示无显著相关性,进一步说明各数据在不同阶段和不同模糊程度下出于独立,可以进行深入的安全性评价分析。
2.2 安全性评估的稳定性、准确性
电厂安全性评价要具有一定的稳定性,否则会导致“误报”,影响后期措施的制定。对比模糊分析法和遗传算法判断安全性评价结果,以验证该文方法的有效性,具体结果见表2。

表2 电厂安全性评价的稳定性、准确性(单位:%)
由表2 可知,两种方法的干扰程度无显著差异(T=0.324,P=0.742),但是,模糊分析法的稳定性、准确性显著优于遗传算法(T=10.851,21.652,P=0.032,0.022)。同时,4 项指标的准确性大于90%,稳定性大于80%,大于遗传算法的80%,75%。而且,模糊分析法的误差幅值为3~4 小于遗传算法的5~7。究其原因,模糊分析法在电厂安全性评价中增加了安全调节因子、安全互动因子对安全性指标进行调整。相对来说,遗传算法在对电厂安全性评价时,由于持续监测产生大量的冗余数据,导致分析结果存在较大误差。为了进一步验证表2 中的结果,将两种方法进行对比并持续监测,结果如图1 所示。
由图1 可知,模糊分析法的结果更加集中,结果为93%~98%,而遗传算法的结果为82%~86%,而且结果比较分散。参照平滑线可知,模糊分析法更加平滑,显著优于遗传算法,说明前者更加平稳,安全性评价更加。其原因是模糊分析法通过插值函数进行模糊值插入,保证分析的稳定性,持续进行安全监测。同时,拟合度曲线显示,遗传算法的拟合度相对较好,但模糊算法的拟合度比较平顺,所以遗传算法的拟合度比模糊算法略差。模糊算法通过模糊理论对数据进行分析,减少数据之间的变化幅度,并对关键性的数据进行提取,不仅减少了数据之间的差异性,而且提高了数据计算的整体稳定性。遗传算法的数据相对来说比较凌乱,而且呈现分散式分布,模糊算法的周边数据分布比较均匀,中间数据相对较为集中,进一步证明了模糊算法的整体结构优于遗传算法。
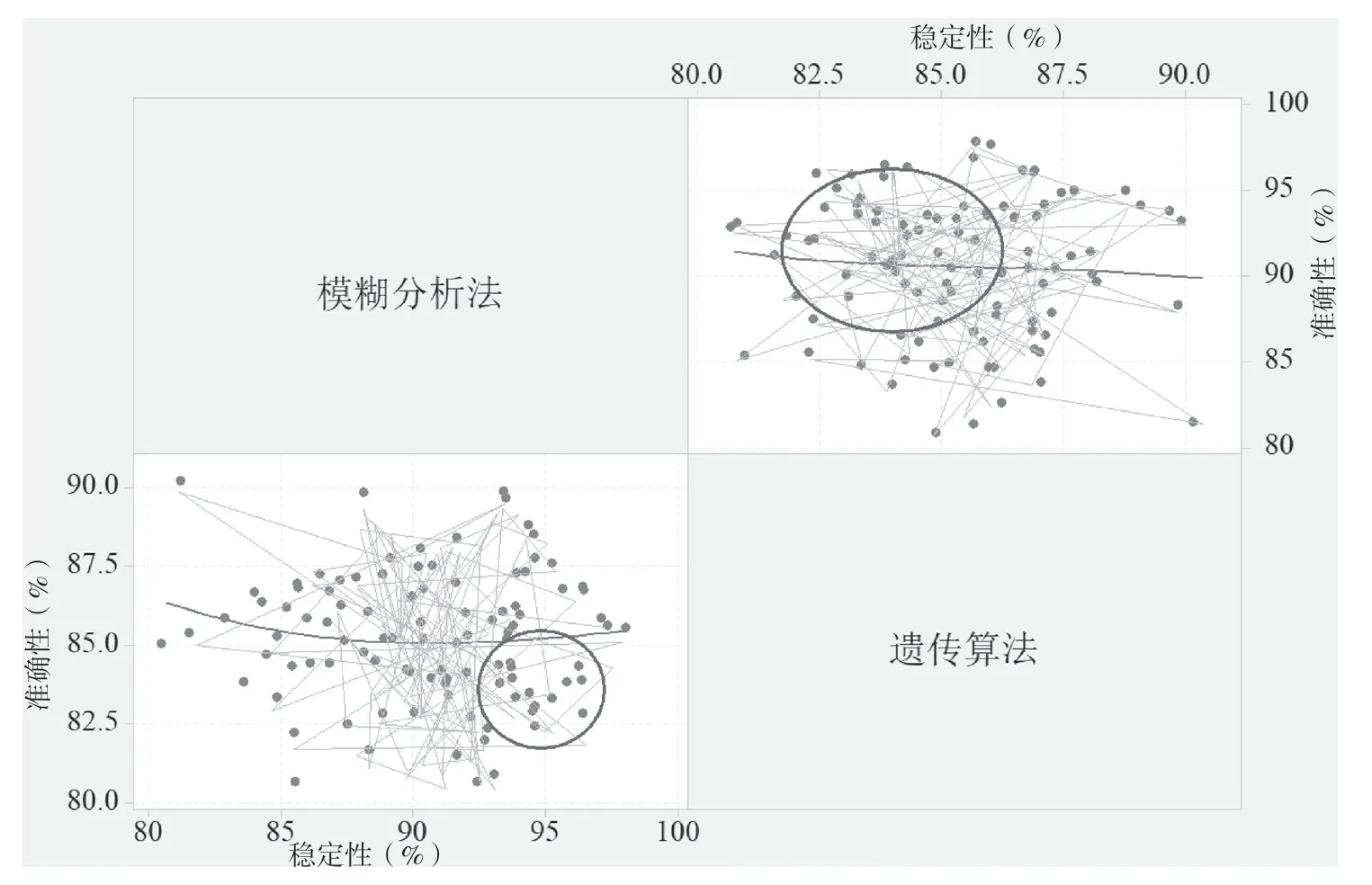
图1 两种方法的准确性和稳定性比较
2.3 安全性评估时间
评估时间是安全性评估的重要内容,该文对安全性指标进行评价分析,并将不同算法的计算时间进行对比,结果见表3。

表3 不同方法的安全性评估时间(单位:s)
根据表3 可知,模糊分析法对电厂安全性评价的时间较短,优于遗传算法。同时,在电厂安全性评价的1/2、1/4和1/6 阶段,各安全性评价指标的评价时间均比遗传算法要短。其中,功率和潮流的计算时间虽然较长,但是模糊分析法的时间优于遗传算法。另外,模糊分析法的误差小于0.3,而遗传算法的误差大于0.5。究其原因,模糊分析法中利用相似性对电厂安全性数据进行分类,并对不同类的值进行阈值比较,不仅减少计算的数据量,而且提高数据的处理效率,大幅提高安全性评估时间。将电压、电流和功率等参数进行比较发现,模糊分析法在不同监测阶段的数据值比较稳定,误差率相对较少。但是,遗传算法的不同阶段监测数据变化幅度较大,而且呈现较大的波动趋势,甚至在1/4 阶段出现了负向波动,进一步说明遗传算法在持续监测过程中存在数据不稳定或数据异常的问题。在误差方面,遗传算法的误差为0.5~0.6,整体的计算结果均大于模糊分析法。其原因主要是模糊分析法对数据进行归类,减少无关数据对结果的影响,并对关键数值进行深入挖掘,在分析各项指标的过程中,都存在指标变化准确和指标综合分析性强的优势。整体来说,模糊算法在各项指标的分析中,均优于遗传算法并且显著提高了算法的整体性能。
3 结论
模糊分析法是一种基于模糊理论的分析方法,对电厂安全性数据进行预处理,剔除无关数据属性。同时,将电压、电流、潮流和功率等指标数据进行相似分析,简化安全性评估流程。同时,融入安全调节因子、安全互动因子,对电厂安全性进行持续监测,及时调整安全系数,发现异常数据。MATLAB 仿真结果显示如下:1)2 种方法的干扰程度无显著差异(T=0.324,P=0.742),但是模糊分析法的稳定性、准确性显著优于遗传算法(T=10.851,21.652,P=0.032,0.022)。同时,4 项指标的准确性大于90%,稳定性大于80%,大于遗传算法的80%,75%。而且,模糊分析法的误差幅值为3~4 小于遗传算法的5~7。2)模糊分析法的结果更加集中,处于93%~98%,而遗传算法的结果处于82%~86%,而且结果比较分散。参照平滑线可知,模糊分析法更平滑,显著优于遗传算法,说明前者更加平稳,安全性评价更加。3)模糊分析法对电厂安全性评价的时间较短,优于遗传算法。同时,在电厂安全性评价的1/2、1/4 和1/6 阶段,各安全性评价指标的评价时间均短于遗传算法。

